Книга: Магия математики: Как найти x и зачем это нужно
Назад: Классика геометрии
Дальше: Теорема Пифагора
Периметры и площади
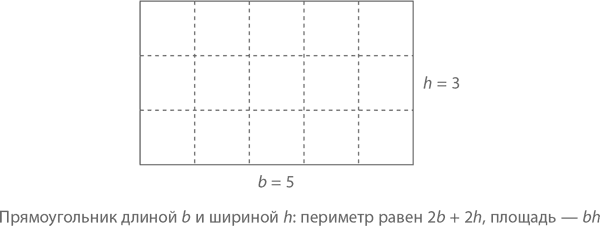
Периметр полигона есть сумма длин его сторон. Так, периметр прямоугольника длиной b и шириной h будет равен 2b + 2h, потому что и b, и h суть размеры каждой из двух его сторон. А как насчет площади? Исходим из того соображения, что площадь квадрата размером 1 на 1 (так называемого единичного квадрата) равна 1. При положительных целых значениях b и h (как на рисунке) мы можем разбить всю площадь на bh единичных квадратов, а значит, она будет равна bh. В целом же, любой прямоугольник с длиной b и шириной h (где b и h суть положительные, но необязательно целые величины) имеет площадь bh.
Отступление
В этой главе мы уже не раз обращались к помощи алгебры, чтобы разрешить исключительно геометрические проблемы. Принцип этот прекрасно работает и в обратную сторону: порой геометрия значительно облегчает понимание алгебры. Взгляните на типичную задачу. Насколько малым может быть значениегде x есть любое положительное число? При x = 1 имеем 2, при x = 1,25 – 1,25 + 0,8 = 2,05, при x = 2 – 2,5. Логика подсказывает, что наименьшим ответом будет 2, и это на самом деле так, только вот как нам в этом удостовериться? Самый простой и эффективный метод расчета будет предложен в главе 11, пока же давайте ограничимся методом геометрическим.
Возьмем фигуру, состоящую из четырех костяшек домино, каждая из которых имеет размер x на 1/x. Расположены они так, чтобы в пространстве между ними получился квадрат. Какова будет общая площадь всей фигуры (включая этот внутренний квадрат)?
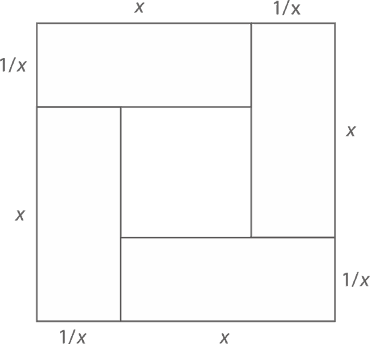
С одной стороны, поскольку фигура представляет собой квадрат x + 1/x на x + 1/x, ее площадь должна быть (x + 1/x)². С другой стороны, площадь каждой костяшки домино равна 1, поэтому площадь фигуры в целом составит как минимум 4. Следовательно,(x + 1/x)² ≥ 4
или x + 1/x ≥ 2, что и требовалось доказать.☺
Начав с площади прямоугольника, можно найти площадь практически любой другой геометрической фигуры, в первую очередь – треугольника.
Теорема: Площадь треугольника с длиной основания b и высотой h составляет 

Для наглядности возьмем три конкретных треугольника, основание каждого из которых рана b, а высота – h, что значит, что их площадь также должна быть равна. Это, по сути, наш третий вопрос, ответ на который, готов поспорить, многих из вас удивил.
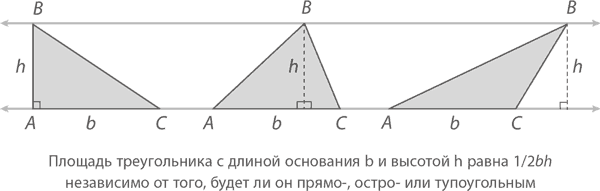
В зависимости от того, какие размеры имеют прилежащие к основанию AC углы ∠A и ∠C, нам нужно рассмотреть три разных частных случая, а затем создать копию треугольника ABC и вписать его вместе с оригиналом в прямоугольник с площадью bh, как показано на рисунке. Треугольник ABC займет ровно половину этой площади, а значит, его площадь составит  как мы и предполагали.
как мы и предполагали.
 как мы и предполагали.
как мы и предполагали.
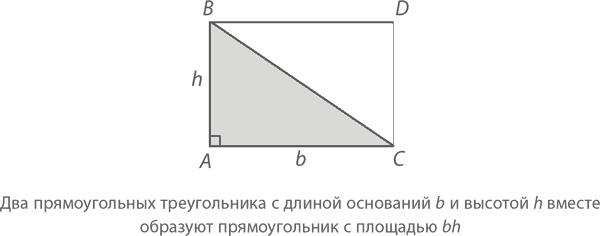
Если углы ∠A и ∠C острые, остроумным будет и доказательство. Из точки B проведите линию длиной h так, чтобы она была перпендикулярна отрезку AC (она называется высотой треугольника ABC), пересекая его в точке X, как показано на рисунке:
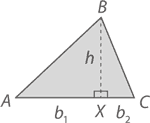
AC, таким образом, состоит из отрезков AX и XC, длины которых составляют соответственно b1 и b2, где b1 + b2 = b. А так как треугольники BXA и BXC получились у нас прямоугольными, то, согласно предыдущему примеру, их площади будут равны 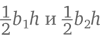 соответственно. Следовательно, площадь большого треугольника ABC –
соответственно. Следовательно, площадь большого треугольника ABC –
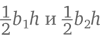 соответственно. Следовательно, площадь большого треугольника ABC –
соответственно. Следовательно, площадь большого треугольника ABC –
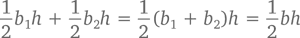
что и требовалось доказать.
В случае же, если ∠A или ∠C является тупым, чертеж будет выглядеть вот так:
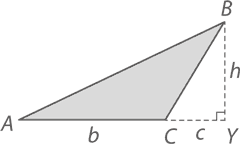
В примере с остроугольным треугольником мы представляли ABC как сумму двух прямоугольных треугольников. Здесь же нам нужна их разность. Высота любом тупоугольном треугольнике выходит за его границы, образуя тем самым большой треугольник. В нашем случае это ABY, длина основания которого равна b + c, а площадь – 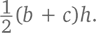 Маленький же прямоугольный треугольник CBY имеет площадь
Маленький же прямоугольный треугольник CBY имеет площадь 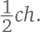 Следовательно, площадь ABC может быть представлена как
Следовательно, площадь ABC может быть представлена как
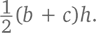 Маленький же прямоугольный треугольник CBY имеет площадь
Маленький же прямоугольный треугольник CBY имеет площадь 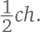 Следовательно, площадь ABC может быть представлена как
Следовательно, площадь ABC может быть представлена как
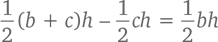
что и требовалось доказать.
Назад: Классика геометрии
Дальше: Теорема Пифагора

