В предыдущих разделах мы описали два основных аспекта дельта-нейтральной и частично-направленной опционных стратегий: (1) расположение и протяженность границ дельта-нейтральности, (2) характеристики, определяющие структуру и свойства доступных опционных портфелей. Теперь необходимо объединить эти два аспекта в общую концепцию построения и выбора оптимального дельта-нейтрального портфеля.

Границы дельта-нейтральности представляют собой множество портфелей, объединенных одним общим признаком – их дельта равна нулю. В этом отношении все они одинаковы. Однако эти портфели очень сильно разнятся по многим другим важным характеристикам. По сути, эти характеристики определяют целый комплекс качеств, от которых зависят риски и доходность создаваемой торговой стратегии. В этом разделе мы продемонстрируем методику определения структуры и свойств портфелей, находящихся на границах дельта-нейтральности. Хотя формально все портфели, расположенные на этой границе, пригодны для использования в рамках любой опционной стратегии, необходимо выбрать из них единственный вариант (или несколько равнозначных альтернатив), обладающий наилучшими характеристиками. В этом разделе мы будем использовать примеры, относящиеся к дельта-нейтральной торговой стратегии. Однако описанная ниже методика может быть в равной мере применена к любой опционной стратегии. (Проблеме выбора оптимального портфеля будет посвящен следующий раздел.)

Для того чтобы определить характеристики дельта-нейтральных портфелей, необходимо выполнить следующие процедуры:

1. Представить границу дельта-нейтральности в виде последовательности точек, каждая из которых задается парой координат на плоскости (порог критерия × диапазон страйков). Поскольку теоретически граница может состоять из бесконечного количества точек, необходимо определить некий дискретный шаг для определения координат точек. Для обоих параметров, «порог критерия» и «диапазон страйков», мы примем этот шаг равным 1 %.

2. Представить зависимость исследуемой характеристики от порога критерия и диапазона страйков в виде топографической карты. (Ранее эти зависимости были представлены в виде трехмерных графиков, см. рис. 1.4.11–1.4.13 и 1.4.16–1.4.19.) Горизонтальная и вертикальная оси карты соответствуют значениям параметров «порог критерия» и «диапазон страйков», а высотная отметка каждой точки на карте выражает значение характеристики, соответствующее определенному портфелю.

3. Нанести на топографическую карту соответствующую ей границу дельта-нейтральности. Координаты точек, составляющих границу, будут соответствовать координатам дельта-нейтральных портфелей. Высотные отметки карты в месте нахождения точек будут соответствовать значениям, принимаемым исследуемой характеристикой.

4. Повторяя последовательно процедуры 1–3 для каждой характеристики, мы получим набор всех характеристик для каждого дельта-нейтрального портфеля.

На рис. 1.6.1 показан результат выполнения первых трех процедур для характеристики «вероятность убытка». В этом примере использовались те же данные, что и в предыдущем разделе: дата создания портфелей 11 января 2010 г., даты экспирации – 15 января 2010 г. (для недельных опционов) и 19 марта 2010 г. (для двухмесячных опционов). Точки и границы дельта-нейтральности были определены с помощью методики, описанной в разделе 1.4.3. Топографическая карта была построена, основываясь на принципах, применявшихся ранее для построения рис. 1.4.3 и 1.4.8. И, наконец, границы и карты были построены в общей системе координат (рис. 1.6.1), что позволит нам определить величину характеристики «вероятность убытка» для каждого дельта-нейтрального портфеля. Высотные отметки топографической карты показывают вероятность убытка для каждого портфеля, находящегося на границе дельта-нейтральности (равно как и для всех прочих, не интересующих нас портфелей, находящихся вне этой границы).

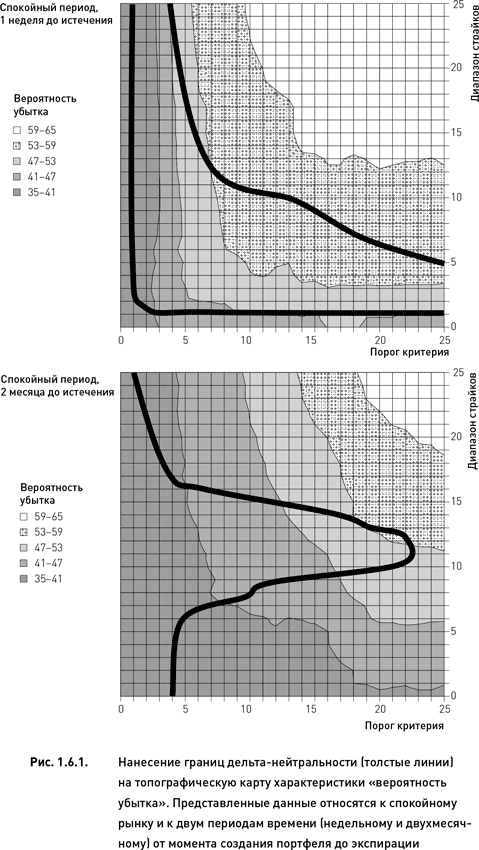
Рис. 1.6.1 визуально представляет процедуры определения характеристик дельта-нейтральных портфелей, однако он не позволяет получить точные значения этих характеристик (поскольку высотные отметки на топографической карте представляются в виде интервалов значений). Кроме того, создание автоматизированной торговой стратегии исключает визуальный анализ и требует разработки расчетного алгоритма. Продемонстрируем процедуру определения точных значений характеристики «вероятность убытка» на примере данных, представленных на верхней карте рис. 1.6.1 (когда портфели формировались из опционов с ближайшей датой истечения).

В этом случае были получены две границы дельта-нейтральности. Одна из них проходит сначала параллельно оси диапазона страйков, а затем резко поворачивает и идет вдоль оси порога критерия (мы не будем рассматривать эту границу, поскольку все портфели на ней имеют очень низкие значения либо одного, либо другого параметра). Вторая граница пересекает топографическую карту от верхней левой части к правой нижней области (портфели на этой границе имеют самые разнообразные сочетания значений двух параметров). Заменим топографическую карту таблицей, ячейки которой отображают вероятности убытка, соответствующие всем возможным вариантам (порог критерия × диапазон страйков). В таблице 1.6.1 ячейки, соответствующие точкам дельта-нейтральности, отмечены серым цветом. Обратите внимание, что расположение серых ячеек повторяет форму границы дельта-нейтральности на верхнем рис. 1.6.1. Значения серых ячеек выражают вероятности убытков соответствующих им дельта-нейтральных портфелей. Такой способ определения характеристик портфелей достаточно прост, легко программируем и исключает влияние субъективного фактора, неизбежного при визуальном анализе графиков.

В предыдущих разделах мы разобрали методику нахождения множества дельта-нейтральных портфелей и научились определять их характеристики. Теперь необходимо сделать следующий шаг – из доступного множества портфелей, удовлетворяющих основному условию (дельта-нейтральности), выбрать такой вариант, характеристики которого наилучшим образом соответствуют требованиям разработчика торговой стратегии. Забегая вперед, заметим, что достичь полного соответствия почти никогда не удается. Поэтому задачу выбора портфеля следует сформулировать следующим образом: из множества доступных альтернатив выбрать такую, характеристики которой наиболее близки к некоему эталону, определяемому разработчиком стратегии.

Для того чтобы продемонстрировать основные подходы к решению задачи выбора, рассмотрим полный комплекс характеристик всех дельта-нейтральных портфелей, полученных в двух случаях. В одном случае портфели формируются во время спокойного рынка из недельных опционов, в другом случае – из двухмесячных опционов. Ранее мы определили значения характеристики «вероятность убытка» для этих двух случаев (рис. 1.6.1). Теперь рассмотрим все прочие характеристики. Для каждой характеристики необходимо построить таблицу (аналогичную таблице 1.6.1) и зарегистрировать значения «серых» ячеек, соответствующих точкам дельта-нейтральности. Обратите внимание, что границы дельта-нейтральности для месячных и недельных опционов заметно отличаются (рис. 1.6.1). Соответственно, отличаются и распределения «серых» точек дельта-нейтральности в пределах таблиц, относящихся к ближайшим и дальним опционам.

Чтобы не перегружать изложение материала избыточным объемом промежуточных таблиц, мы не будем приводить здесь отдельные таблицы для каждой характеристики. Вместо этого, сведем в единую таблицу характеристики, относящиеся только к дельта-нейтральным портфелям (только «серые» ячейки). Это позволит получить общее представление о полном комплексе характеристик, относящихся ко всем доступным вариантам дельта-нейтральных портфелей.

Характеристики дельта-нейтральных портфелей показаны в таблицах 1.6.2 (портфели формировались из краткосрочных опционов) и 1.6.3 (портфели формировались из долгосрочных опционов). Для того чтобы приступить к анализу характеристик и выбору на их основе оптимального портфеля, следует определить для каждой характеристики интервалы ее допустимых значений. Данные интервалы зависят от требований, предъявляемых к разрабатываемой стратегии, а также от индивидуальных предпочтений разработчика и от накладываемых на него внешних ограничений. Поэтому в каждом конкретном случае интервалы допустимых значений могут быть разными. В нашем случае мы будем использовать следующие интервалы:

• Количество комбинаций: от 20 до 200;

• Количество базовых активов: от 20 до 100;

• Соотношение длинных и коротких комбинаций: от 20 до 80 % коротких комбинаций;

• Вероятность убытка: менее 50 %;

• Асимметричность портфеля: коэффициент асимметричности не более 0,1.

• VaR: не более 600.

В таблицах 1.6.2 и 1.6.3 мы использовали серый цвет для обозначения интервалов допустимых значений. В пределах каждой колонки таблицы серый цвет обозначает приемлемые интервалы для каждой отдельно взятой характеристики. В пределах каждой строки серый цвет показывает, являются ли значения характеристик данного портфеля допустимыми.

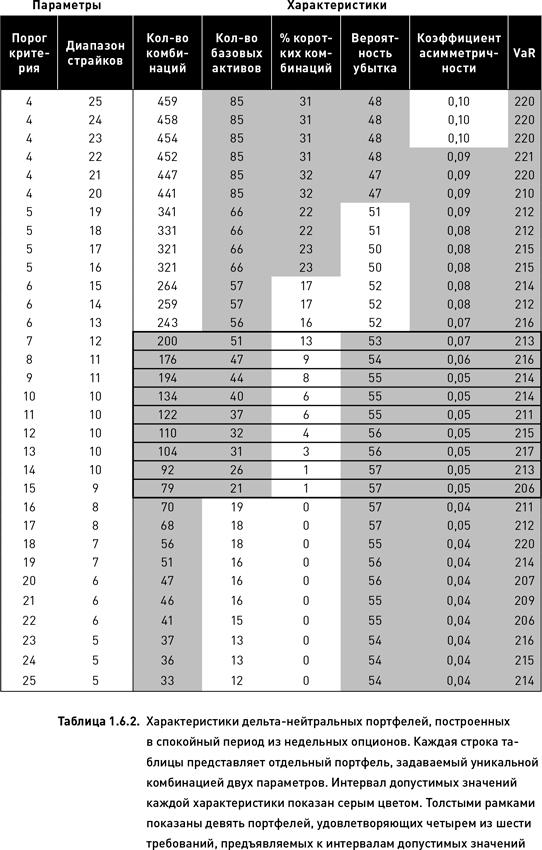
В том случае, когда портфели формировались из ближайших опционов, ни один из них не обладал таким набором характеристик, который полностью удовлетворял бы нашим требованиям (таблица 1.6.2). Не нашлось даже ни одного портфеля, удовлетворяющего хотя бы пяти из шести требований, предъявляемых к интервалам допустимых значений. Зато сразу девять портфелей обладают характеристиками, четыре из которых удовлетворяют предъявляемым требованиям. Эти портфели обозначены толстыми рамками в таблице 1.6.2. Подходит ли из этих девяти портфелей хотя бы один для открытия позиций, зависит от алгоритма выбора, принятого разработчиком стратегии (ниже мы коснемся этого вопроса подробнее).

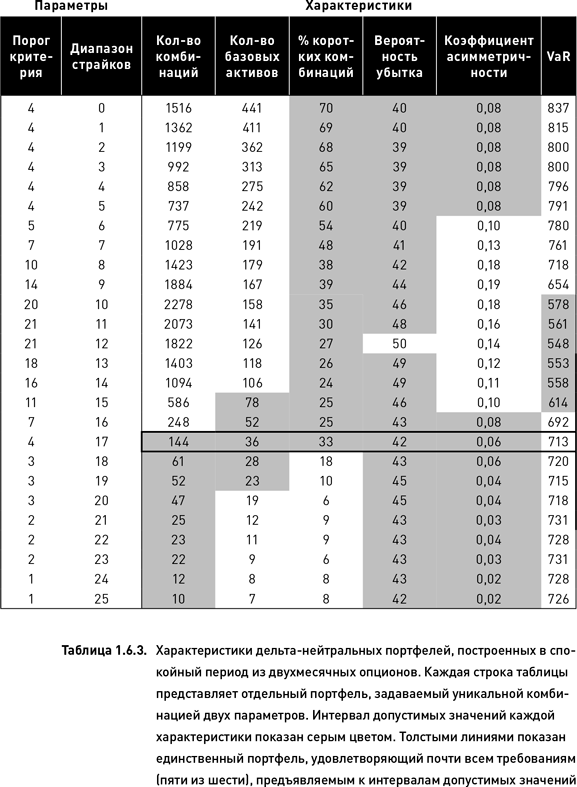
В том случае, когда портфели создавались на основе далеких опционов, также ни один из них не обладал полностью удовлетворительным набором характеристик (таблица 1.6.3). Зато пять из шести характеристик одного портфеля удовлетворяли требованиям, предъявляемым к интервалам допустимых значений. Этот портфель обозначен толстой рамкой в таблице 1.6.3. Если, в соответствии с алгоритмом выбора, этого достаточно, то такой портфель может быть использован для открытия торговых позиций.

Можно предложить большое количество алгоритмов выбора оптимального портфеля. По существу, все они являются вариантами решения задачи многокритериального анализа, в которой каждая характеристика представляет собой отдельный критерий.

Самый суровый алгоритм может иметь следующий вид. На первом этапе выбираются только те портфели, все характеристики которых удовлетворяют априорно установленным требованиям. (В наших двух примерах не нашлось ни одного такого портфеля.) На втором этапе существует несколько вариантов действий. Можно ранжировать все характеристики по степени их значимости. После чего из множества портфелей, отобранных на первом этапе, выбирается один с наилучшим значением первой по важности характеристики. Если таких портфелей окажется несколько, то дальнейший отбор производится с помощью второй по важности характеристики. И так далее. Недостаток такого подхода заключается в том, что весьма затруднительно упорядочить все характеристики по степени их важности (многие из них равнозначны). Другой вариант второго этапа заключается в применении Паретовского метода многокритериального отбора. Однако в этом случае мы будем лишены возможности контролировать количество выбираемых опционных портфелей. Этот недостаток может оказаться весьма существенным, поскольку выбор нескольких портфелей вместо одного означает необходимость открытия гораздо большего количества позиций, что негативно скажется на потерях за счет проскальзывания и операционных издержек.

Менее суровый алгоритм может выглядеть так. На первом этапе выбираются все портфели, n из m характеристик которых удовлетворяют требованиям, предъявляемым к интервалу их допустимых значений. В наших примерах число характеристик равно 6 (m = 6). Если принять n = 5, то в примере, представленном таблицей 1.6.3, найдется единственный портфель, прошедший первый этап отбора, а в таблице 1.6.2 не окажется ни одного такого портфеля. Зато если принять n = 4, то в таблице 1.6.2 будет сразу девять портфелей, прошедших первый этап отбора (обозначены толстыми рамками в таблице). Второй этап может быть реализован теми же двумя путями, что были описаны для сурового алгоритма. Например, если считать наиболее важной характеристикой «количество комбинаций» (чем их меньше, тем лучше, но не менее 20), то из девяти альтернатив на втором этапе будет выбран портфель, определяемый параметрами (порог критерия = 15, диапазон страйков = 9). Можно пойти и другим путем. Из множества вариантов, прошедших первый этап отбора, на втором этапе можно выбрать портфель, имеющий наилучшие значения по тем характеристикам, которые не попали в интервал допустимых значений. В таблице 1.6.2 все девять портфелей имеют неудовлетворительные значения по характеристикам «процент коротких комбинаций» и «вероятность убытка». Однако портфель, определяемый параметрами (порог критерия = 7, диапазон страйков = 12), имеет по этим характеристикам лучшие показатели, чем остальные восемь портфелей. Этот портфель и может быть выбран в качестве оптимального.

Как для сурового, так и для более мягкого алгоритма реализация второго этапа может основываться на другом принципе. Вместо априорного ранжирования характеристик по степени их важности, можно принять в качестве основной ту характеристику, значения которой изменяются в более широком диапазоне, чем значения других характеристик. Например, в таблице 1.6.2 все значения характеристик «коэффициент асимметричности» и VaR лежат в очень узком интервале значений. Поэтому все девять портфелей, прошедших первый этап отбора, почти не отличаются друг от друга по этим характеристикам. Следовательно, не имеет никакого смысла выбирать их в качестве основных ориентиров для второго этапа выбора. С другой стороны, значения характеристик «количество комбинаций» и «количество базовых активов» варьируют в широком диапазоне значений (от 79 до 200 и от 21 до 51 соответственно). Поэтому в данном конкретном случае будет естественным использовать эти характеристики в качестве основных для окончательного выбора оптимального портфеля.

Необходимо подчеркнуть, что какой бы алгоритм выбора оптимального портфеля ни был принят к реализации при разработке автоматизированной торговой стратегии, от него во многом зависит, какой из вариантов дельта-нейтрального портфеля будет в конечном итоге использован для открытия позиций.