Рубеж второй: Виолончель
3
Всякий принимает пределы своего собственного поля зрения за пределы мира.Артур Шопенгауэр
Когда я начинал учиться в средней школе, наш учитель музыки спросил, хочет ли кто-нибудь из класса научиться играть на музыкальном инструменте. Руки подняли мы трое. Учитель подвел нас к шкафу, чтобы показать, какие инструменты можно выбрать. В совершенно пустом шкафу лежали стопкой три трубы.
– Судя по всему, вы будете учиться играть на трубе.
Я не жалею о своем выборе (хотя никакого выбора и не было). Я отлично провел время, играя в городском оркестре и дурачась в группе медных духовых оркестра графства, пока мы отсчитывали такты паузы. Но все-таки я немножко завидовал струнным: казалось, что они играли все время и именно им доставались лучшие мелодии. Несколько лет назад меня спросили в интервью на радио, на каком новом музыкальном инструменте я хотел бы научиться играть, будь у меня такая возможность, и какое произведение я бы хотел сыграть на нем.
– На виолончели. Сюиты Баха.
Этот вопрос продолжал меня преследовать и после интервью: могу ли я научиться играть эти прекрасные сюиты для виолончели? Может быть, осваивать новый инструмент было уже слишком поздно, но мне нужно было это узнать. И я купил себе виолончель.
Сейчас, когда я пишу о попытках предсказать результат броска игральной кости, виолончель стоит у меня за спиной. Когда мне нужно отвлечься от анализа уравнений, которые управляют поведением красного кубика, лежащего у меня на столе, я начинаю мучить одну из джиг из первой сюиты для виолончели. Я чувствую, как Бах переворачивается в гробу, но мне это занятие нравится.
Одна из увлекательных возможностей игры на виолончели заключается в скользящем движении пальца вверх по струне для получения непрерывного глиссандо разных нот. На трубе такого не сделаешь – это инструмент отдельных нот, соответствующих разным комбинациям нажатых клапанов. Оказывается, что борьба между непрерывным глиссандо виолончели и дискретными нотами трубы тоже имеет отношение к моим попыткам предсказать поведение игральной кости.
Увеличение картинки
Чтобы предсказать, как может упасть кость, нужно знать, из чего она сделана. Если плотность ацетатного пластика в одном из углов кубика выше, чем в других, то одна из сторон будет выпадать чаще других. Поэтому, чтобы попытаться применить законы Ньютона к летящей в воздухе кости, нужно знать, как она сделана. Непрерывна ли ее структура, или же, если присмотреться, она собрана из отдельных деталей?
Если я смирюсь с пределами моего зрения в соответствии с цитатой из Шопенгауэра, приведенной в начале этого «рубежа», то я увижу только сплошной красный ацетат, из которого сделана кость. Однако при помощи оптического микроскопа я могу увеличить кость в 1500 раз, до размеров большого здания. Заглянув внутрь такой огромной кости, я по-прежнему мало что узнаю о тайнах ее строения. Все по-прежнему выглядит довольно гладким и непрерывным.
Микроскопы, использующие различные части электромагнитного спектра, появившиеся в XX в., позволили ученым получать изображения с увеличением, в 1000 раз большим. Теперь моя игральная кость простирается от одного конца Лондона до другого. И на этом уровне увеличения она выглядит более зернистой. На смену ощущению непрерывной структуры приходит нечто более дискретное. Современные электронные микроскопы позволяют увеличить изображение еще в 10 раз, и тогда я смогу различать атомы углерода и водорода, которые, как мне известно, составляют часть ингредиентов ацетатного пластика, из которого изготовлена моя кость.
Интересно, что ученые сформулировали атомарное представление о строении материи задолго до того, как у меня появилась возможность увидеть эти атомы под электронным микроскопом в лаборатории, расположенной через дорогу от моей кафедры математики. И именно сочетание математической и теоретической точек зрения с физическим видением мира дает лучшие средства познания того, из чего сделана эта кость.
Однако атомы, в том числе водорода, кислорода и углерода, оказались не столь атомарными, как предполагает их название. Я знаю, что за атомной структурой, видимой под электронным микроскопом, существует более глубокая внутренняя структура. Атомы уступают место электронам, протонам и нейтронам. Место протонов и нейтронов, в свою очередь, занимают кварки. В 2013 г. при помощи квантовых микроскопов даже удалось получить изображения электронных орбиталей возле ядра атома водорода. Но существует ли теоретический предел той глубины, которой я могу достигнуть в исследовании внутреннего строения своей кости?
Например, что случится, если я буду все время разрезать и разрезать кость пополам? До чего я могу дойти? С математической точки зрения я не вижу никаких проблем: если у меня есть число, его можно делить на два сколько угодно раз:
1, 1/2, 1/4, 1/8, 1/16 …
Математика не определяет точки, в которой мне пришлось бы остановиться. Однако если я возьму реальную игральную кость, которая лежит у меня на столе, и разрежу ее пополам, а потом еще раз пополам, как далеко я смогу зайти?
Противоречия между непрерывной и дискретной природой материи, между математическими возможностями и ограничениями, налагаемыми физической реальностью, бушуют уже многие тысячелетия. Под какую музыку танцует Вселенная – под звуки трубы или под глиссандо виолончели?
Музыка сфер
Откуда я знаю про электроны и кварки, которые считаются последним уровнем строения моей игральной кости? Я их никогда не видел. Если спрошу себя, как я, собственно, узнал о них, я отвечу, что столько раз о них слышал и читал, что уже и не помню, как и откуда. И вообще, говорили ли мне когда-нибудь, откуда мы о них знаем? Например, я знаю еще, что самая высокая гора – это Эверест. Я знаю об этом только потому, что достаточно много раз об этом слышал. Так что, прежде чем выяснять, существует ли что-то кроме этого уровня, следовало бы понять, как мы пришли к этим составным элементам.
Читая историю, с удивлением обнаруживаешь: убедительные доказательства того, что такие объекты, как моя кость, не просто имеют непрерывную структуру, а состоят из дискретных элементов, называемых атомами, были получены всего чуть более столетия назад. Но хотя это открытие было сделано сравнительно недавно, интуитивное ощущение такого положения вещей возникло тысячи лет назад. Индусы считали, что материя состоит из основных атомов, соответствующих вкусу, запаху, цвету и осязанию. Они разделяли атомы на бесконечно малые, не занимающие никакого места, и другие, «крупные» и занимающие конечное пространство, – и, как мы увидим дальше, рассматривая современную модель строения вещества, эта теория была чрезвычайно прозорливой.
На Западе атомистическую философию природы первыми предложили древние греки, придерживавшиеся редукционистской точки зрения, согласно которой физическая реальность может быть сведена к фундаментальным блокам, из которых состоит вся материя. Такие атомы невозможно разделить на меньшие составляющие, и их свойства не должны зависеть от какого-либо еще более сложного внутреннего строения. Одним из источников такой веры во Вселенную, составленную из отдельных блоков, было убеждение пифагорейской школы в том, что число является ключом к объяснению тайн Вселенной.
Вера в могущество целых чисел проистекает из довольно замечательного открытия, приписываемого самому Пифагору: оно состояло в том, что число лежит в основе музыкальной гармонии, которую использует как виолончель, так и труба. Говорят, что его прозрение случилось, когда он проходил мимо кузницы и услышал в стуке молота сочетание гармоничных нот (мы не знаем, можно ли верить этой и другим подобным историям о Пифагоре и даже существовал ли вообще такой человек, или же он был выдуман последующими поколениями для пропаганды новых идей).
Как бы то ни было, согласно этой истории, он вернулся к себе домой и стал экспериментировать с нотами, получаемыми на струнном инструменте. Взяв вибрирующую струну виолончели, я могу получить непрерывную последовательность нот, постепенно перемещая палец в сторону подставки. Так я получаю звук, называемый глиссандо (хотя на следующем «рубеже» вопрос о том, образуется ли при этом действительно непрерывная последовательность нот, будет поставлен под сомнение). Если я остановлюсь в том положении, в котором получаются ноты, звучащие в гармонии с вибрирующей открытой струной, окажется, что отношение длин этих струн точно равно целому числу.
Например, прижав пальцем середину вибрирующей струны, я получу ноту, звучащую почти так же, как нота, с которой я начал. Интервал между ними называется октавой, и для человеческого уха эта нота звучит настолько похоже на ноту открытой струны, что в музыкальной нотации мы обозначаем их одним и тем же названием. Если я помещу свой палец в одной трети расстояния от головки грифа, я получу ноту, особенно гармонично звучащую в сочетании с нотой открытой струны. Такой интервал называется чистой квинтой, и наш мозг реагирует на подсознательное узнавание целочисленного отношения длин волн этих двух нот.
Обнаружив, что в основе гармонии лежат целые числа, пифагорейцы начали строить модель Вселенной, в которой такие целые числа были фундаментальными кирпичиками всего, что они видели и слышали вокруг себя. В греческой космологии царила идея небесной математической гармонии. Считалось, что между орбитами планет существуют идеальные математические соотношения, что и породило идею музыки сфер.
Для понимания структуры игральной кости важнее то обстоятельство, что ключом к объяснению состава материи пифагорейцы считали дискретные числа, а не непрерывное глиссандо. Они предложили идею атомов, которые подобно числам можно складывать для образования новой материи. Греческий философ и математик Платон, развивая пифагорейскую философию, представил такие атомы дискретными геометрическими элементами.
Платон полагал, что атомы представляют собой геометрические фигуры, треугольники и квадраты. Из этих элементарных блоков были составлены формы, которые считались основными ингредиентами греческой химии, – элементы, или «стихии» огня, земли, воздуха и воды. Каждая стихия, по мнению Платона, имела собственную трехмерную геометрическую форму.
Огонь имел форму треугольной пирамиды, или тетраэдра, образованного из четырех равносторонних треугольников. Форма земли была кубической, подобно моей игральной кости из Лас-Вегаса. Воздух был образован из формы, называемой октаэдром, которая состоит из восьми равносторонних треугольников. Она выглядит как две пирамиды, склеенные своими квадратными основаниями. Наконец, вода соответствовала икосаэдру, составленному из двадцати равносторонних треугольников. Платон считал, что химия стихий возникает из геометрического взаимодействия таких основных форм.
Атомистическое видение материи не было повсеместно признано в Древнем мире. В конце концов, никаких доказательств существования таких невидимых элементов не было. Их нельзя было увидеть. Аристотель, например, не верил в идею фундаментальных атомов. Он полагал, что стихии по природе своей непрерывны, так что мою игральную кость теоретически можно делить на все меньшие и меньшие части. Он считал огонь, землю, воздух и воду элементарными в том смысле, что их нельзя разделить на «тела иной формы». Сколько бы мы их ни делили, мы всегда получаем воду или воздух. Вода в стакане представляется человеческому глазу непрерывной структурой, которую теоретически можно делить до бесконечности. Кусок резины можно плавно растянуть так, что он будет казаться непрерывным. Так было подготовлено поле битвы между непрерывной и дискретной моделями материи. Между глиссандо и дискретными нотами музыкальной гаммы. Между виолончелью и трубой.
Интересно отметить, что именно пифагорейцам приписывается открытие, которое поставило атомистическое видение материи под угрозу и на долгие годы изменило ситуацию в пользу веры в возможность бесконечного деления материи.
Числа на грани
Если провести на листе бумаги две линии, то с атомистической точки зрения каждая из линий будет состоять из определенного числа неделимых атомов и, следовательно, их длины будут пропорциональны некоторым целым числам, соответствующим количествам атомов, их составляющих. Но оказалось, что такой строгий порядок не вполне соответствует положению вещей. Более того, именно теорема о прямоугольных треугольниках самого Пифагора показала, что мир геометрии способен порождать линии, отношение длин которых не может быть выражено простыми дробями.
В размерах моей игральной кости уже таится некоторое затруднение для этого атомистического воззрения на природу. Возьмем два ребра кубика, расположенные под прямым углом друг к другу. Их длины равны. Рассмотрим диагональ, проведенную по грани кубика и завершающую треугольник, образованный вместе с двумя ребрами одинаковой длины. Каково отношение длины этой диагонали к длинам более коротких сторон треугольника?
Как гласит теорема Пифагора о прямоугольном треугольнике, квадрат длины такой диагонали (гипотенузы) равен сумме квадратов длин двух коротких сторон (катетов). Если считать длину ребра кубика равной 1, то, по теореме Пифагора, длина диагонали грани такого кубика равна числу, квадрат которого равен 2. Что же это за число?
Задача вычисления этой длины увлекала еще вавилонян. Оценку этой длины можно найти на хранящейся в Йельском университете табличке, которую датируют старовавилонским периодом (1800–1600 гг. до н. э.). Используя шестидесятеричную систему (т. е. систему счисления по основанию 60), вавилоняне получили следующий результат:
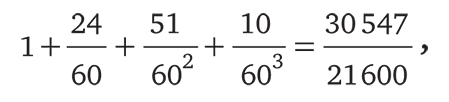
которому при десятичной записи соответствует число 1,41421296296…, причем группа «296» повторяется до бесконечности. Собственно, любая дробь, будучи записана в десятичной системе, с какого-то момента начинает повторяться. Это вавилонское вычисление было замечательным достижением. Оно соответствует точному результату до шестого знака после запятой. Однако квадрат этой дроби оказывается чуть меньше 2. Открытие древних греков состояло в том, что, как бы ни старались вавилонские писцы, их дроби, возведенные в квадрат, никогда не могли быть точно равны 2.
Открытие неизбежности такой неудачи вавилонских математиков приписывают одному из последователей Пифагора по имени Гиппас. Он доказал, что длина диагонали грани моей игральной кости в принципе не может быть выражена в виде дроби.
Из теоремы Пифагора о прямоугольном треугольнике следует, что длина гипотенузы равна произведению длины катета на квадратный корень из 2. Но Гиппас смог доказать, что дроби, квадрат которой был бы точно равен 2, не существует. Доказательство использует один из классических приемов, имеющихся в арсенале математика, – доказательство от противного. Гиппас предположил сначала, что существует такая дробь, квадрат которой равен 2. При помощи некоторых ловких преобразований можно показать, что из этой посылки всегда следует противоречивый вывод о существовании числа одновременно четного и нечетного. Единственный способ разрешения этого противоречия состоит в признании ложности исходного предположения: существование дроби, квадрат которой был бы равен 2, невозможно.
Говорят, что его товарищи-пифагорейцы были приведены в смятение вестью о том, что их прекрасные прямоугольные треугольники могут порождать такие негармоничные длины. Члены секты поклялись молчать об этом, но, когда Гиппас обнародовал свои результаты, его, как рассказывают, утопили в море за разглашение факта существования в физическом мире подобной дисгармонии. Однако заткнуть рот этим новым числам, называемым иррациональными, поскольку они не являются отношениями целых чисел, было сложнее.
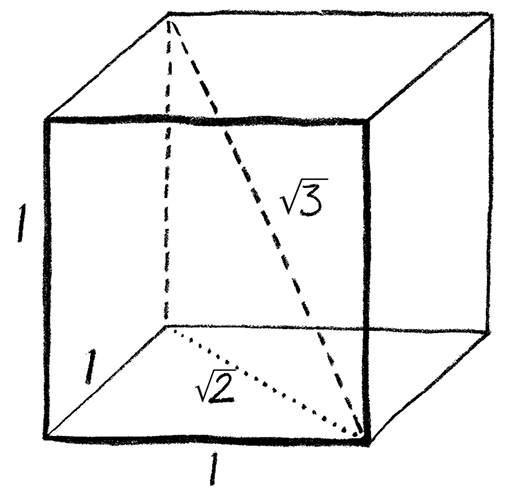
Иррациональные длины в кубе
Мне конечно же кажется, что такая длина существует. Я могу увидеть ее на линейке, приложенной к длинной стороне треугольника. Она равна расстоянию между двумя противоположными углами любой грани моей кости. И тем не менее, сколько бы я ни пытался, я не могу найти закономерность этого бесконечного десятичного числа. Оно начинается с 1,414213562… и продолжается до бесконечности, никогда не повторяясь.
Иррациональный восторг
Открытое древними греками существование длин, которые нельзя выразить простым отношением целых чисел, заставило математиков того времени создать новую математику, математику иррациональных чисел, которая позволила бы действительно измерить Вселенную. Иррациональными оказались и другие базовые длины, например π, длина окружности единичного диаметра, – они тоже не были равны отношениям целых чисел. Хотя иррациональность квадратного корня из 2 была известна древним грекам еще 2000 лет назад, только в XVIII в. швейцарский математик Иоганн Генрих Ламберт смог доказать, что число π тоже не может быть выражено в виде отношения двух целых чисел.
Несмотря на мое отвращение к тому, чего мы знать не можем, один из определяющих моментов, возбудивших во мне любовь к математике, наступил, когда я прочитал о числах, которые не могут быть выражены простым отношением целых чисел. В том же году, когда учитель музыки познакомил меня с трубой, лежавшей в шкафу, учитель математики познакомил меня с доказательством иррациональности квадратного корня из 2. Это доказательство содержалось в одной из книг, которые учитель посоветовал мне прочесть, пытаясь разжечь во мне математическое пламя. И это ему удалось. Я был поражен тем, что при помощи конечного логического рассуждения можно доказать, что размер, подобный длине диагонали квадрата, может быть выражен лишь числом с бесконечным количеством знаков. А если записать такую длину невозможно, мне нужно хотя бы понять, почему это число нельзя познать.
С тех пор как я школьником прочитал это доказательство, я узнал о других методах исследования иррациональных чисел, так что, может быть, эти числа все-таки познаваемы. Существуют бесконечные выражения с регулярной структурой, позволяющие сделать такие числа менее таинственными. Например,
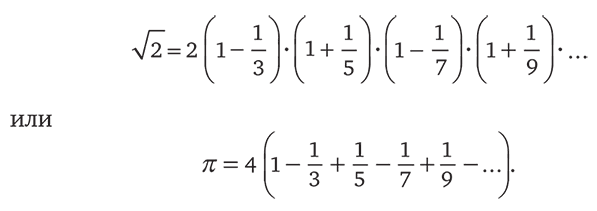
Открытие таких выражений выводит иррациональные числа в область известного. Дробь представляет собой число, которое при десятичной записи повторяется начиная с некоторой точки. Нельзя ли рассматривать такие выражения как структуру, не слишком отличную от повторяющейся группы десятичного представления дроби? Наличие такой повторяющейся группы означает, что существуют два числа, отношение которых дает значение данного числа, тогда как в случае 2 и π я вынужден использовать для выражения этих длин бесконечное число чисел. Вопрос о том, обязательно ли известное должно быть конечным, будет постоянно преследовать меня в течение всего моего путешествия к границам неизвестного.
Разумеется, для любого практического применения таких чисел мне, вероятно, хватит и приближения, выраженного дробью. Большинство инженеров вполне успешно использует вместо числа π его оценку 22/7, которую Архимед получил путем приближения окружности 96-сторонним правильным многоугольником. Собственно говоря, чтобы вычислить длину окружности размером с наблюдаемую часть Вселенной с точностью, сравнимой с размерами атома водорода, достаточно знать всего 39 знаков π. Существует даже формула, позволяющая узнать значение миллионного знака π без вычисления всех предшествующих ему знаков. Не то чтобы мне так уж хотелось их знать. Но такая формула позволяет достичь лишь конечного знания числа, полное познание которого требует бесконечности.
Из открытия таких чисел, по-видимому, следовала бесконечная делимость пространства. Только бесконечное деление пространства может позволить мне точно измерить размеры моего простого кубика. В результате этого открытия мнение Аристотеля о непрерывности материи оставалось на Западе господствующим вплоть до эпохи Возрождения.
Гармония маленьких сфер
Благодаря научным открытиям, сделанным поколением Ньютона и после него, произошел новый разворот в сторону мнения о том, что Вселенная построена из неких элементарных кирпичиков. Пожалуй, первым в аристотелевском видении материи, господствовавшем почти 200 лет, усомнился современник Ньютона Роберт Бойль. В своей книге «Химик-скептик» Бойль попытался опровергнуть идею о том, что материя составлена из четырех «стихий» – огня, земли, воздуха и воды. Такое описание, возможно, хорошо отражает состояния материи, но не ее составляющие.
Взамен он предложил новый список химических элементов. Более того, он высказал утверждение, по тем временам довольно сильно попахивавшее ересью. Он считал, что такие элементы представляют собой миниатюрные тела, или атомы, различающиеся лишь «размером, видом, текстурой и движением». С точки зрения теологии такая идея казалась опасной; Церковь, всегда предпочитавшая воззрения Аристотеля, увидела в ней признаки опасно материалистического видения мира. Кое-кто объявил Бойля Галилеем химической революции.
Хотя Ньютон был согласен с тезисом Бойля о том, что материальный мир состоит из неделимых элементов, те математические инструменты, которые Ньютон разрабатывал одновременно с работой Бойля, в сильной степени основывались на бесконечной делимости времени и пространства. Математический анализ, позволяющий сделать моментальный снимок непрерывного потока развития Вселенной, имеет смысл только в качестве процесса, в котором пространство делят на все меньшие и меньшие фрагменты и интерпретируют то, что происходит в пределе бесконечного уменьшения таких фрагментов.
Вопрос о бесконечной делимости времени и пространства возбуждал философские дискуссии еще со времен древнегреческого мыслителя Зенона Элейского, сформулировавшего парадоксы, которые, по-видимому, следовали из такого деления пространства. Например, Зенон утверждал, что стрела никогда не сможет долететь до цели, потому что она должна сначала преодолеть половину расстояния до цели, потом половину оставшегося расстояния, потом половину вновь оставшегося расстояния и т. д., так что достижение цели потребовало бы бесконечного числа таких перемещений. Успех ньютоновского математического анализа вновь возродил обсуждение этой проблемы. Некоторые все еще считали такую бесконечную делимость почти что ересью.
Епископ Беркли посвятил целый трактат под названием «Аналитик» доказательству абсурдности попыток деления на ноль. Его направленность была ясно выражена в подзаголовке «Рассуждение, адресованное неверующему математику».
Хотя другие неверующие математики быстро осознали могущество математического анализа, остальные открытия самого Ньютона подтверждали предположение о том, что, даже если пространство и время можно делить бесконечно, к материи это не относится. Его идея мира, составленного из неделимой материи, со временем стала господствующей теорией устройства Вселенной. Но в тот момент она все еще оставалась просто одной из теорий, мало чем подтвержденной.
Теория сил, воздействующих на крупные объекты – будь то планеты или яблоки, – была столь успешной, что Ньютон предположил, что раз эти принципы верны для чрезвычайно крупных объектов и объектов среднего размера, то они должны быть применимы и к чрезвычайно малому. С чего бы законам движения, управляющим поведением Вселенной, изменяться по мере увеличения масштаба моей игральной кости? Успешность применения математического анализа к движению планет была основана на их представлении в виде точечных масс, расположенных в центрах тяжести соответствующих тел. Может быть, и вся материя состоит из частиц, подобных миниатюрным планетам, поведение которых определяется законами движения. В своих «Началах» Ньютон предположил, что применение его идей к таким отдельным частицам позволило бы предсказать поведение всех материальных объектов.
Ньютоновская теория света также способствовала распространению убеждения в том, что атомистическое воззрение является наилучшим способом понимания мира. Представление света в виде частиц казалось простейшим путем к описанию явлений, которые Ньютон изложил в своей «Оптике». Казалось, что отражение света имитирует поведение бильярдного шара, отскакивающего от бортов стола. Но с научной точки зрения никаких эмпирических свидетельств правоты такой теории Вселенной, состоящей из отдельных частиц, не было.
Даже при помощи микроскопов, появившихся в XVII в., нельзя было увидеть ничего, подтверждающего эту атомистическую модель. Хотя какие-то дискретные объекты и были видны, доказать их неделимость было невозможно. Тем не менее об изменении господствующего мнения можно судить по распространенности атомистического воззрения в популярной культуре той эпохи. В «Оде святой Цецилии» Николаса Брейди, положенной на музыку в 1691 г. Генри Пёрселлом, упоминаются «зерна материи»:
О мира душа! вдохновленны тобой,
Материи зерна забыли свой бой,
Атомы розны связала ты прочно,
Соединяя в пропорции точной
Несхожие части гармоньей одной.
Наиболее убедительные доказательства атомарного строения вещества были получены веком позже из экспериментов, которые показывали, как в сочетаниях материи образуются новые вещества. И сочетания эти были полны совершенной гармонии, в точном соответствии с образами Брейди.
Атомная алгебра
Первое реальное экспериментальное подтверждение представления о материи, состоящей из отдельных атомов, было получено в начале XIX в. в работах английского химика Джона Дальтона. Он обнаружил, что химические соединения, по-видимому, состоят из веществ, содержащихся в них в целочисленных пропорциях, и это революционное открытие привело ко всеобщему научному признанию идеи о том, что такие вещества действительно существуют в виде дискретных порций.
Например: «Элементы кислорода могут сочетаться с определенной порцией газообразного азота или с удвоенной его порцией, но не с промежуточным количеством». Разумеется, одно это обстоятельство не доказывало дискретности материи и даже не было достаточно сильным аргументом, чтобы переубедить приверженцев непрерывной модели. Но оно содержало в себе недвусмысленный намек. Должно было существовать какое-то объяснение такому свойству сочетания веществ.
Обозначения, принятые для описания таких реакций, способствовали распространению атомистической точки зрения. Сочетание азота с кислородом может быть записано в виде N + O или N + 2O. Между этими вариантами ничего нет. Оказалось, что все соединения содержат пропорции, соответствующие целочисленным отношениям. Например, сульфид алюминия дается формулой 2Al + 3S = Al2S 3, и элементы содержатся в нем в соотношении 2: 3. Элементы никогда не сочетаются иначе чем в целочисленных соотношениях. Создавалось впечатление, что в самом сердце химического мира существует музыкальная гармония. Музыка маленьких сфер.
Русский ученый Дмитрий Менделеев прославился тем, что смог расположить этот растущий список молекулярных ингредиентов так, что в нем начала проявляться закономерность, основанная на целых числах и подсчете. Казалось, возвращается пифагорейская вера в могущество числа. Как и многие ученые до него, Менделеев расположил элементы в порядке возрастания относительного веса, но он смог понять, что для выявления смутно возникающей закономерности необходимо проявить некоторую гибкость.
Он выписал известные элементы на карточки и постоянно раскладывал из них на своем столе своего рода химический пасьянс, пытаясь заставить их раскрыть свои тайны. У него ничего не получалось, и это приводило его в исступление. В конце концов он заснул, обессиленный, и увидел во сне разгадку, а проснувшись, смог разложить карточки по приснившейся ему системе. Один из важных моментов, которые позволили ему успешно расположить элементы, состоял в осознании необходимости некоторых пропусков – то есть понимании того, что в этой колоде не хватает нескольких карт.
Ключом к расположению элементов был так называемый атомный номер, зависящий от числа протонов в атомном ядре, а не от суммарного числа протонов и нейтронов, которое определяет массу ядра. Но, поскольку в то время никто не имел никакого понятия об этих, еще меньших, составляющих, Менделееву приходилось лишь догадываться о причинах, лежащих в основе его системы.
В качестве приблизительной аналогии можно представить себе обычную карточную колоду: карты можно разложить по мастям, но также можно заметить, что во всех мастях есть карты одинакового достоинства. В химических элементах можно было заметить периодичность восьмерок: свойства элементов, расположенных через восемь друг от друга, казались очень похожими. Через восемь элементов от лития находится натрий, еще через восемь – калий. Все они – мягкие, блестящие, химически активные металлы. Похожая закономерность обнаруживается и в газах со сходными свойствами.
Расположение элементов по восьмеркам было замечено еще до открытия Менделеева и называлось законом октав. Восьмерки сравнивали с музыкальными октавами: когда я играю на своей виолончели восемь нот мажорной гаммы, самая высокая и самая низкая ноты звучат очень похоже и даже называются одинаково. Когда Джон Ньюлендс впервые предложил этот закон октав на рассмотрение Королевского общества, его попросту высмеяли. «Вы бы еще сказали, что, для того чтобы понять элементы, их надо расположить в алфавитном порядке!» – пошутил один из академиков. Схема Менделеева до некоторой степени подтвердила справедливость закона октав. Именно благодаря принципу повторяющейся, или периодической, структуры эта система получила название периодической таблицы.
Гениальное прозрение Менделеева состояло в том, что несоответствие некоторых элементов системе может указывать на существование недостающих элементов. Предположение о наличии в таблице пробелов было, возможно, самым ярким проявлением его проницательности. Например, пустое место в 31-й клетке таблицы позволило Менделееву предсказать в 1871 г. существование и свойства нового вещества, впоследствии названного галлием. Четыре года спустя французский химик Лекок де Буабодран выделил первые образцы этого нового элемента, предсказанного благодаря математическим закономерностям, открытым Менделеевым.
Рецепт приготовления игральной кости
Итак, мы получили список атомов, из которых, по-видимому, состоит вся материя. Например, наша игральная кость состоит из сочетания атомов углерода, атомов кислорода и атомов водорода, объединенных в структуру, называемую ацетилцеллюлозой. Мое собственное тело тоже в основном состоит из сочетаний тех же атомов, но объединенных в другие структуры. Ацетилцеллюлоза представляет собой однородную структуру, лишенную пузырей, что увеличивает вероятность ее равномерности. Раньше игральные кости делали из нитроцеллюлозы, которую изобрел в 1868 г. Джон Уэсли Хайат. Составленный им коктейль из азотной кислоты, серной кислоты, хлопчатого волокна и камфары давал удивительный материал с высокой прочностью на разрыв, устойчивый к воздействию воды, масел и даже слабых кислот.
Брат Хайата назвал его целлулоидом, и этот материал стали чрезвычайно выгодно использовать для изготовления вещей, которые до того вырезали из рога или слоновой кости. Из этого синтетического пластика изготавливались бильярдные шары и съемные воротнички, фортепианные клавиши и даже игральные кости. В начале XX в. изготовление костей из нитроцеллюлозы было промышленным стандартом, но через несколько десятилетий использования таких костей с ними происходила почти моментальная кристаллизация, и они рассыпались, выделяя газообразную азотную кислоту.
Игральные кости, сделанные для казино Лас-Вегаса в конце 1940-х гг. и избежавшие кристаллизации, стали теперь коллекционными. Моей кости такая судьба не грозит. На следующей иллюстрации показано, как расположены атомы внутри моей кости.
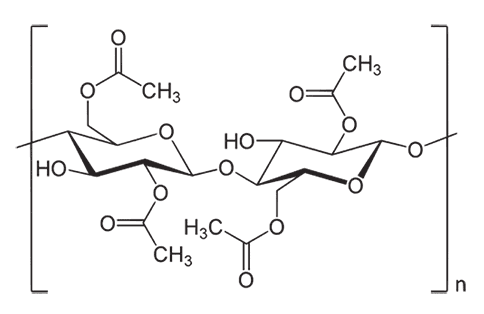
Идентификация этих элементов еще не была доказательством справедливости дискретной модели строения материи. Ничто не говорит о том, что такая картинка ингредиентов игральной кости не может соответствовать какой-нибудь формуле сочетания непрерывных структур. В то время как химики склонялись к атомистическому видению Вселенной, среди физиков такие взгляды были далеко не столь общепринятыми. Тех, кто подобно немецкому физику Людвигу Больцману предлагал атомарную модель материи, в исследовательских лабораториях высмеивали.
Больцман считал атомарную теорию мощным средством интерпретации концепции теплоты, основанной на идее газа, состоящего из мельчайших молекул, которые соударяются друг с другом подобно огромному множеству микроскопических бильярдных шаров. Теплота попросту представляет собой суммарную кинетическую энергию таких движущихся миниатюрных шаров. Применение этой модели в сочетании с вероятностными и статистическими методами позволило ему объяснить макроскопическое поведение газов. Но большинство физиков по-прежнему были привержены идеям непрерывности материи и относились к идеям Больцмана пренебрежительно.
Насмешки над Больцманом дошли до такой степени, что ради публикации своих идей ему пришлось отречься от своей веры в соответствие «бильярдной» теории строения материи действительной реальности и называть ее эвристической моделью. Эрнст Мах, главный противник Больцмана в дискуссии о реальности атомов, издевательски спрашивал его: «Вы сами когда-нибудь видели атом?»
Больцман был подвержен приступам депрессии и, судя по некоторым признакам, мог страдать биполярным расстройством. Считается, что неприятие его идей научным сообществом усугубило его депрессию, под влиянием которой в 1906 г., будучи на отдыхе в Триесте вместе со своей семьей, он и повесился, когда его жена с дочерью ушли купаться.
Его смерть была тем более трагической, что именно в это время стали появляться убедительные доказательства его правоты. Причем подтверждавшие атомистическую картину мира идеи, от которых к тому же было невозможно отмахнуться, принадлежали одному из самых влиятельных физиков. Тем, кто подобно Маху продолжал верить в непрерывную структуру мира, было чрезвычайно непросто объяснить результаты исследования броуновского движения, полученные Эйнштейном и другими.
Пылевой пинг-понг
Хотя обычные оптические микроскопы и не позволяют увидеть отдельные атомы, они позволили ученым XIX в. увидеть воздействие таких атомов на окружающую их среду. Это воздействие называется броуновским движением по имени Роберта Броуна, который в 1827 г. заметил случайное движение мельчайших частиц пыльцы, плавающих на поверхности воды. Поскольку пыльца – вещество органическое, Броун сначала решил, что ее прыжки по поверхности могут быть признаками жизни. Сходное случайное движение угольной пыли, плавающей на поверхности спирта, наблюдалось в 1785 г. голландским ученым Яном Ингенхаузом. Когда Броун увидел, что поведение пыльцы может быть свойственно и неорганической материи, он не мог понять, какие причины могут вызывать такое беспорядочное движение.
Интересно отметить: идею о том, что речь может идти о невидимых атомах, сталкивающихся с более крупными видимыми частицами вещества, высказал еще древнеримский поэт Лукреций в своей философской поэме «О природе вещей»:
Вот посмотри: всякий раз, когда солнечный свет проникает
В наши жилища и мрак прорезает своими лучами,
Множество маленьких тел в пустоте, ты увидишь, мелькая,
Мечутся взад и вперёд в лучистом сиянии света;
[…]
Кроме того, потому обратить тебе надо вниманье
На суматоху в телах, мелькающих в солнечном свете,
Что из неё познаёшь ты материи также движенья,
Происходящие в ней потаённо и скрыто от взора.
[…]
Первоначала вещей сначала движутся сами,
Следом за ними тела из малейшего их сочетанья,
Близкие, как бы сказать, по силам к началам первичным,
Скрыто от них получая толчки, начинают стремиться,
Сами к движенью затем понуждая тела покрупнее.
Так, исходя от начал, движение мало-помалу
Наших касается чувств, и становится видимым также
Нам и в пылинках оно, что движутся в солнечном свете,
Хоть незаметны толчки, от которых оно происходит.
Эти стихи были написаны в 60 г. до н. э., но для подтверждения такого атомарного объяснения случайного движения пылинок в солнечном луче у Лукреция и пыльцы у Броуна потребовался математический анализ Эйнштейна.
Нужно было предложить какую-то модель, которая воспроизводила бы странное движение частиц пыльцы на поверхности воды. Если наложить на такую поверхность координатную сетку, кажется, что частица пыльцы может с равной вероятностью двигаться влево, вправо, вверх или вниз. Ее движение похоже на перемещения пьяного человека, который совершает случайные шаги, как бы подчиняясь результатам бросков четырехсторонней игральной кости. На приведенной внизу картинке показаны траектории движения разных частиц пыльцы, которые зарисовал французский физик Жан Батист Перрен, взявшийся за решение задачи о движении пыльцы в своей книге «Атомы».
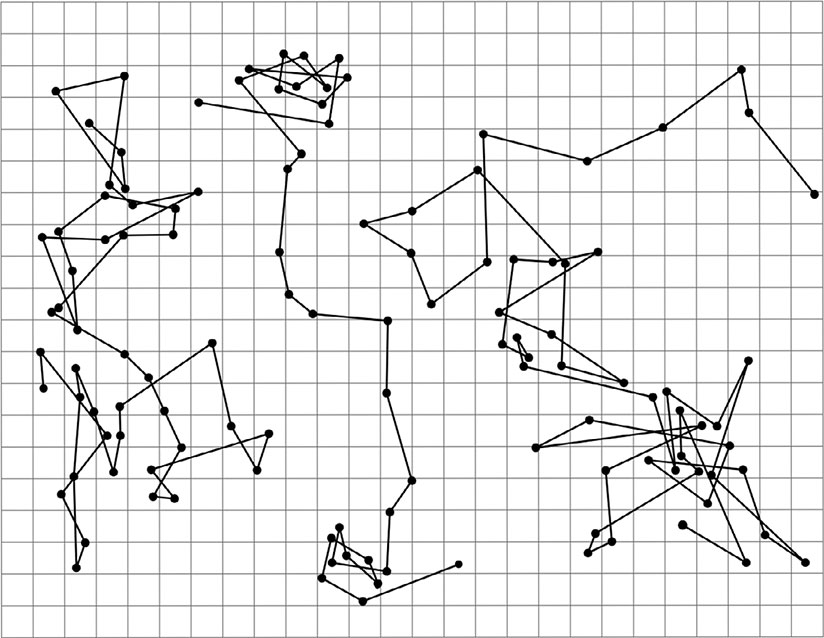
В начале XX в. возникло предположение, что наблюдаемый эффект связан с толчками, которые частицы пыльцы получают в результате движения гораздо меньших молекул воды.
Математический гений Эйнштейна позволил ему проанализировать модель, в которой крупный объект подвергается соударениям со значительно меньшими его объектами, движущимися случайным образом. Он доказал, что такая модель точно предсказывает наблюдаемое поведение. Представим себе каток, в центре которого лежит большая хоккейная шайба, а затем введем целую систему маленьких шайб, скользящих в случайных направлениях с определенными скоростями. Маленькие шайбы будут время от времени сталкиваться с большой, вынуждая ее двигаться в некотором направлении. Тонкость состояла в определении числа маленьких шайб и их относительных размеров, необходимых для получения наблюдаемого поведения большой шайбы.
Успешное воспроизведение движения пыльцы математической моделью, разработанной Эйнштейном, стало сокрушительным ударом для всех тех, кто считал, что жидкость, подобная воде, представляет собой сплошную субстанцию. Любому, кто еще верил в Аристотелево видение материи, было бы чрезвычайно трудно предложить столь же убедительное объяснение.
Вычисления позволили оценить, насколько малы молекулы воды по сравнению с частицами пыльцы, которые они толкают. Хотя тем самым было получено убедительное доказательство того, что материя состоит из дискретных частей, вопрос о возможности дальнейшего бесконечного деления таких частей на еще меньшие части оставался открытым.
И действительно, неделимые атомы оказались вовсе не неделимыми, когда были открыты еще меньшие составные части, образующие, например, атомы углерода или кислорода. На следующем, более глубоком, уровне оказалось, что атом собран из еще меньших «шайб», называемых электронами, протонами и нейтронами, причем первые из них были обнаружены еще за несколько лет до революционного теоретического открытия Эйнштейна.
Разборка атома
Вот как работает наука: у нас есть модель Вселенной, которой мы можем придерживаться до тех пор, пока не обнаружится нечто, что в нее не встраивается, нечто новое, что, по-видимому, нельзя объяснить при помощи имеющейся модели. Понимание того, что атом может быть составлен из еще меньших частей, возникло из экспериментов, обнаруживших существование чего-то, похожего на частицы, но гораздо меньшего, чем атомы, составляющие периодическую систему.
Эти мельчайшие, подобные частицам объекты возникли в экспериментах, которые проводил в конце XIX в. британский физик Дж. Дж. Томсон, пытаясь понять природу электричества. Он изучал электропроводность газов. В его ранних экспериментах использовалась стеклянная трубка, на обоих концах которой было установлено по электроду. При приложении к электродам высокого напряжения между ними возникал электрический ток. Странным было то, что этот ток можно было увидеть, так как между электродами появлялась световая дуга.
Еще более странные вещи произошли, когда Томсон полностью удалил из трубки газ и приложил напряжение к вакууму. Световая дуга исчезла. Но, к его удивлению, стекло на одном из концов трубки стало флюоресцировать. Когда в трубку вставили металлический крест, в центре светящегося флюоресцирующего пятна появилась крестообразная тень.
Тень появилась напротив отрицательно заряженного электрода, также называемого катодом. Самое правдоподобное объяснение состояло в том, что катод испускает какие-то лучи, которые взаимодействуют с материей – будь то газ, содержащийся в трубке, или, в случае вакуума, стекло самой трубки – и заставляют ее светиться.
Эти «катодные лучи» вели себя довольно загадочно. Выяснилось, что они проникают сквозь тонкие листки золотой фольги, помещенные на их пути. Могут ли они быть неким волновым явлением, подобным свету? Другие полагали, что они состоят из отрицательно заряженных частиц, выталкиваемых отрицательным и притягиваемых положительным электродом. Но как такие частицы могут проходить сквозь твердое золото?
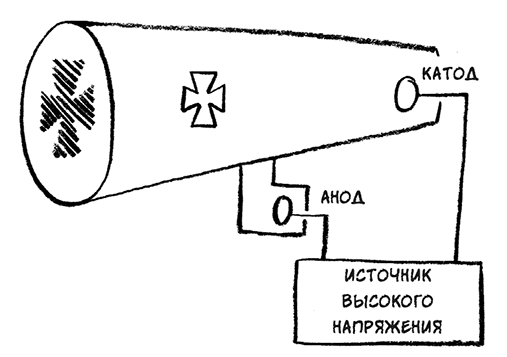
Испущенные из катода электроны соударяются с противоположной стенкой, вызывая флюоресценцию стекла
Томсон считал, что если речь действительно идет об отрицательно заряженных частицах, то он сможет изменить траекторию их полета в трубке, поместив ее в магнитное поле. Немецкий физик Генрих Герц уже пытался это сделать и потерпел неудачу, но Герц недостаточно хорошо откачал из трубки газ, что и привело к искажению результатов эксперимента. Когда газ откачали, все получилось так, как рассчитывал Томсон. К лучам приложили магнитное поле, и тень действительно сдвинулась. Магнит изгибал катодные лучи.
Но самый удивительный результат был получен, когда Томсон произвел математический расчет предполагаемой массы таких заряженных частиц. При приложении силы к массе, в соответствии с законами движения Ньютона, степень ее смещения зависит от массы. Поэтому степень отклонения лучей, вызываемого магнитным полем, содержит в себе информацию о массе предполагаемых частиц.
Результат вычислений зависит еще и от заряда частицы, и, измерив его в отдельном эксперименте, Томсон смог вычислить ее массу. Результат был поразительным. Масса частицы была почти в 2000 раз меньше массы атома водорода, самого маленького из атомов периодической системы.
То, что такие частицы, по-видимому, вылетали из металла, из которого был изготовлен электрод, заставило предположить, что они представляют собой составные части атома. Атом все-таки оказался делимым. В нем нашлись меньшие части. Их назвали электронами (от древнегреческого слова ἤλεκτρον, обозначающего янтарь, то есть первое вещество, в котором был найден электрический заряд).
Открытие того факта, что атомы содержат еще меньшие составные части, потрясло мировоззрение многих ученых. Вот что случилось после одной из лекций, на которых Томсон рассказывал о своих результатах:
Много времени спустя один известный физик, бывший на моей лекции, признался, что думал тогда, будто я их разыгрываю.
Следующий уровень
Даже когда Томсон использовал катод из другого металла, масса испускаемых им частиц не изменилась. Казалось, что такие частицы являются составляющими всех атомов. Сначала предположили, что атом водорода, масса которого в 2000 раз больше массы электрона, должен состоять из 2000 таких электронов. Но атом гелия приблизительно в 2 раза тяжелее атома водорода. Почему же число электронов перескакивает с 2000 на 4000, а между этими числами ничего нет? Целочисленные отношения масс атомов периодической системы были одной из причин считать, что они имеют действительно атомарную природу. Как же объяснить такие ступенчатые изменения массы? Кроме того, атомы электрически нейтральны. Существуют ли другие частицы, заряд которых уравновешивает отрицательный заряд электронов? Можно ли заставить атомы испускать положительно заряженные частицы, содержащиеся в них в дополнение к отрицательно заряженным электронам?
На самом деле экспериментальные свидетельства испускания лучей положительно заряженных частиц, вылетающих в противоположном направлении, существовали. Такие лучи было значительно труднее отклонить при помощи магнитного поля, что заставляло предположить, что эти частицы массивнее электронов. В этом случае интересная особенность заключалась в том, что масса таких частиц, по-видимому, изменялась в зависимости от того, каким газом была заполнена трубка. В случае водорода их масса была приблизительно равна массе исходного атома. Казалось, что у атомов водорода, содержащегося в трубке, отбирали электроны, причем оставались крупные положительно заряженные частицы, притягивавшиеся к противоположному электроду.
Томсону удалось добиться аналогичного эффекта в других газах – гелии, азоте, кислороде. Массы были равны произведениям целых чисел на массу положительно заряженных частиц, полученных из атомов водорода. Снова получалась атомная гармония. И тем не менее не было никаких оснований полагать, что существует множество типов положительно заряженных частиц, соответствующих множеству типов атомов. Томсон предложил модель атома, известную под названием «пудинга с изюмом». Положительно заряженная часть атома, более массивная, чем отрицательно заряженные электроны, образует «пудинг», занимающий большую часть объема атома, а электроны соответствуют маленьким изюминкам, расположенным внутри пудинга.
Затем наступила эпоха бомбардировки атомов, которая в конце концов привела к созданию самого мощного из существующих ускорителей – Большого адронного коллайдера в ЦЕРН. Честь открытия протона, частицы-кирпичика, из которого построены все положительно заряженные частицы, исследовавшиеся Томсоном, обычно приписывают британскому физику Эрнесту Резерфорду, родившемуся в Новой Зеландии.
Резерфорда увлекла новая в то время тема радиоактивности. Атомы урана, по-видимому, испускали частицы, которые можно было регистрировать на фотопластинках. Казалось, что существуют два типа радиоактивности, которые стали называть альфа-частицами и бета-частицами. Альфа-частицы было легче зарегистрировать. Резерфорд обнаружил, что при помощи магнитного поля такие альфа-лучи можно отклонять так же, как Томсон отклонял свои отрицательно заряженные частицы. Расчеты показали, что масса альфа-частиц совпадает с массой атома гелия, лишенного электронов. Догадка о том, что альфа-лучи, испускаемые ураном, есть не что иное, как фрагменты атомов гелия, получила подтверждение, когда альфа-лучи объединили с потоком электронов, в результате чего произошло образование устойчивого газа. Химический анализ вскоре подтвердил, что этот газ действительно был гелием.
Баллистика и папиросная бумага
Экспериментальные результаты в очередной раз вступили в противоречие с теоретической моделью атома, когда ученик Резерфорда Ханс Гейгер поместил тонкий лист золотой фольги между потоком альфа-частиц и пластиной, регистрирующей частицы. В соответствии с моделью атома, в которой положительный заряд распределен равномерно, как тесто в пудинге, положительно заряженные альфа-частицы, пролетающие сквозь металл, должны испытывать отталкивание со стороны положительного заряда атома. Поскольку заряд распределен равномерно по всему объему атома, значительного отклонения частиц ожидать не приходится.
Гейгер обнаружил, что, вопреки ожиданиям, некоторые альфа-частицы отклонялись в самые разные стороны, вплоть до отражения от золотой фольги непосредственно в том направлении, с которого они прилетели. Резерфорд был ошеломлен: «Это было почти так же невероятно, как если бы вы выстрелили 15-дюймовым снарядом в лист папиросной бумаги, а снаряд вернулся бы назад и попал в вас».
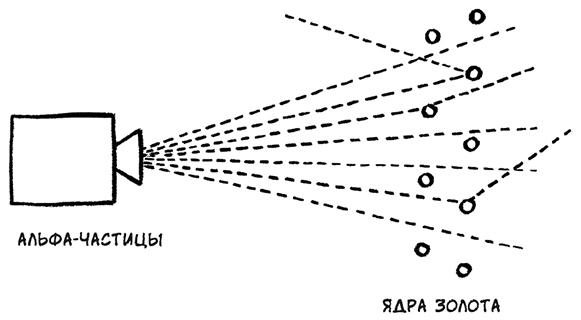
Отклонение альфа-частиц ядрами атомов золота
Новая модель и на этот раз возникла из математических расчетов. Подсчитав, сколько альфа-частиц отклонилось и на какой угол, исследователи обнаружили, что данные соответствуют конфигурации, в которой заряд и масса сосредоточены в малоразмерном объекте в центре атома, который стали называть ядром. Было ли такое ядро неделимым, оставалось неясным.
Когда Резерфорд стал бомбардировать альфа-частицами более легкие атомы, появились свидетельства того, что ядро не является единым объектом, но образовано некими составляющими частицами. Отслеживая траектории альфа-частиц в камере Вильсона, он обнаружил траектории, которые были в 4 раза длиннее, чем ожидалось. Такое могло произойти, если бы попадание альфа-частицы выбивало из ядра другую частицу, в 4 раза более легкую. Эксперименты с разными газами дали одинаковые результаты. Более того, Резерфорд обнаружил, что чистый азот в результате такого столкновения превращается в кислород. Выбивание одной из этих частиц приводило к преобразованию химического элемента.
Так было получено свидетельство существования элементов, из которых построены атомные ядра. Они вели себя в точности как атом водорода, лишенный своего электрона. Резерфорд открыл протон. Атомные ядра оказались построены путем соединения нескольких протонов. Единственное затруднение состояло в том, что электрический заряд не сходился. К примеру, масса ядра гелия в 4 раза больше массы атома водорода, а его заряд больше всего вдвое. Возможно, в ядрах существуют электроны, связанные с протонами и уравновешивающие их заряд. Но физические принципы, которые были разработаны для объяснения поведения этих частиц, исключали столь близкое существование электронов и протонов, так что такой ответ не подходил.
В 1920-х гг. это натолкнуло Резерфорда на догадку о возможном существовании третьей составляющей частицы, названной им нейтроном, имеющей приблизительно ту же массу, что и протон, но не имеющей заряда. Получить свидетельства ее существования оказалось крайне непростой задачей. Резерфорд обсуждал со своим коллегой Джеймсом Чедвиком самые безумные способы, которыми можно было бы обнаружить нейтроны. В конце концов в экспериментах, проведенных в 1930-х гг. в Германии и Франции, были обнаружены частицы, испускаемые при бомбардировке различных ядер альфа-частицами, и частицы эти, в отличие от протонов, по-видимому, не имели заряда. Но экспериментаторы ошибочно считали их каким-то типом электромагнитного излучения наподобие высокочастотных гамма-лучей, которые открыл в начале XX в. французский физик Поль Виллар.
Однако Чедвик был убежден, что эти частицы и есть нейтроны, которые он обсуждал с Резерфордом. Дальнейшие эксперименты показали, что их масса чуть превышает массу протона и именно эта новая частица, не имеющая заряда, оказалась тем ингредиентом, которого недоставало для согласования численных результатов. После открытия Чедвика казалось, что все кирпичики, из которых построена материя, наконец обнаружены.
Модель выглядела чрезвычайно привлекательно. Четыре «стихии» Аристотеля – огонь, земля, воздух и вода – были сведены к трем частицам: электрону, протону и нейтрону. Из этих трех кирпичиков, как считали ученые, можно построить всю материю. Кислород: 8 протонов, 8 нейтронов и 8 электронов. Натрий: 11 протонов, 12 нейтронов и 11 электронов. Как будто бы зазвучала музыка сфер, и в основе материи лежали эти три ноты – протоны, электроны и нейтроны. Вся материя, по-видимому, состояла из целочисленных комбинаций этих трех частиц. Какие были основания ожидать, что и сами эти частицы образованы из еще меньших составляющих? Если бы это было так, то можно было бы рассчитывать увидеть дробные сочетания, расположенные между элементами периодической системы.
Но деление на этом не остановилось. Оказалось, что существуют весьма основательные экспериментальные и математические доводы в пользу делимости протонов и нейтронов. Однако кирпичики, составляющие протоны и нейтроны, обладают одним странным свойством: они не любят находиться в одиночестве. Они встречаются только группами, образуя объекты, подобные протонам или нейтронам. Вместе им безопаснее. Но, если такие частицы никто никогда не видел поодиночке, почему же ученые считают, что такие, еще меньшие, части, на которые можно разделить протоны и нейтроны, существуют?

