Книга: О том, чего мы не можем знать. Путешествие к рубежам знаний
Назад: 3
Дальше: Рубеж третий: Банка урана
4
Все, что мы называем реальным, сделано из того, что реальным считать нельзя.Нильс Бор
В конце 1920-х гг. казалось, что все основные кирпичики, из которых построена материя, обнаружены. Все атомы периодической системы можно построить из сочетаний электронов, протонов и нейтронов. Все попытки дальнейшего деления электрона были безуспешными. Но открытия, сделанные в следующие десятилетия, привели ученых к пониманию того, что под остальными двумя кирпичиками скрывается следующий уровень реальности.
Основной толчок к пониманию того, что протоны и нейтроны могут быть не столь неделимыми, как электрон, был дан не какой-нибудь более хитрой технологией, а математическими соображениями симметрии. Поразительно, что лучшим микроскопом для изучения внутреннего устройства моей игральной кости снова и снова оказывается математика. Для объяснения существования протонов и нейтронов разрабатывалась математическая модель, и она была основана на математической концепции, допускавшей деление. А раз математическое представление можно было разделить на более мелкие части, то казалось, что и к самим протонам и нейтронам должен быть применим тот же принцип.
Математическая модель, благодаря которой возникла идея о делимости протона и нейтрона, появилась, когда физики открыли, что в дополнение к трем составляющим элементам устойчивых атомов существует множество других частиц.
Их открыли в экспериментах по столкновениям частиц. Речь шла не о построенных человеком коллайдерах, подобных LHC, а о природных столкновениях, которые происходят в верхних слоях атмосферы при прохождении сквозь нее космических лучей.
Зверинец частиц
Первое свидетельство существования новых частиц было найдено в камерах Вильсона, которые экспериментаторы использовали для восстановления траекторий заряженных частиц. Камера Вильсона состоит из герметичного бака, заполненного перенасыщенными парами воды и спирта. Перенасыщение паров приводит к тому, что любая пролетающая через камеру частица оставляет за собой конденсационный след.
В 1933 г. Карл Андерсон, физик, работавший в Калтехе, использовал такие камеры для подтверждения предсказанного за несколько лет до этого британским физиком Полем Дираком существования странного нового вида материи, называемого антивеществом. Предпринятая Дираком попытка объединения квантовой физики и теории электромагнетизма позволила объяснить многие особенности электронов, но его уравнения имели еще и полностью зеркальное решение, которое не соответствовало ничему, виденному до тех пор в лабораториях.
Уравнения Дирака были в некотором смысле аналогичны уравнению x2 = 4. У этого уравнения есть не только решение x = 2, но и зеркальное ему решение x = –2, так как (–2)2 тоже равно 4. Из зеркального решения уравнений Дирака следовало, что существует зеркальный вариант электрона, имеющий положительный заряд. Большинство считало это решение математическим курьезом, порожденным уравнениями, но, когда четыре года спустя Андерсон заметил в своей камере следы частицы, которая вела себя как электрон, отраженный в зеркале, антивещество перешло из теории в область реальности. Открытые Андерсоном позитроны, как их стали называть, возникли в результате взаимодействия частиц в верхних слоях атмосферы. И они не были единственными вновь появившимися частицами.
Вскоре после этого в камере оставили следы еще более странные частицы, вообще никем не предсказанные. В 1936 г. Андерсон начал анализировать эти новые следы вместе со своим аспирантом Сетом Неддермейером. Новые частицы, обнаруженные в камере Вильсона, были отрицательно заряженными. Но они не были электронами. Следы, оставленные этими новыми частицами, соответствовали значительно большей массе. Массу частицы можно определить по степени отклонения ее траектории в магнитном поле, в точности как это делал Томсон. Эта частица имела заряд, равный заряду электрона, но изогнуть ее траекторию было гораздо труднее.
Частица, называемая теперь мюоном, была одной из первых новых частиц, полученных из взаимодействия космических лучей с атмосферой. Мюон нестабилен. Он быстро распадается на другие частицы, чаще всего на электрон и два нейтрино. Нейтрино было еще одной новой частицей, существование которой было предсказано для объяснения распада нейтронов в протоны. Поскольку нейтрино почти не имеют массы и не имеют электрического заряда, они были экспериментально обнаружены лишь в 1950-х гг., но с теоретической точки зрения они были необходимы для объяснения распада как нейтронов, так и вновь найденных мюонов. Среднее время жизни мюона составляет 2,2 микросекунды, чего хватает, чтобы достаточное количество таких частиц достигло поверхности Земли не распавшись.
Мюоны помогли подтвердить предсказание о замедлении времени при приближении к скорости света, сделанное Эйнштейном в специальной теории относительности. С учетом периода их полураспада число мюонов, достигающих поверхности Земли, должно быть гораздо меньше наблюдаемого. Это противоречие объясняется замедлением времени на околосветовых скоростях. Если бы к мюону можно было прикрепить часы, они показали бы, что до его соударения с Землей прошло меньшее время. Таким образом, большее число мюонов просуществовало бы до этого момента, что и подтверждается экспериментом. Мы еще вернемся к этому вопросу на пятом «рубеже», когда будем рассматривать время и связанные с ним пределы познания.
Мюон казался поразительно похожим на электрон, но более массивным и менее стабильным. Услышав об этом открытии, американский физик Исидор Раби язвительно заметил: «Такого никто не заказывал». Существование в природе более тяжелой и неустойчивой копии электрона казалось странным и ненужным. Раби и не подозревал, как много других частиц еще оставалось в этом меню.
Осознав, что взаимодействие космических лучей с верхними слоями атмосферы порождает новые формы материи, физики решили не ждать, пока частицы долетят до камер, установленных в лабораториях, так как к этому моменту они могут распасться на уже известные виды материи. Поэтому камеры Вильсона стали устанавливать на большей высоте, надеясь поймать в них другие частицы.
Исследователи из Калтеха выбрали вершину горы Вилсон, расположенной вблизи города Пасадены, в котором они работали. И действительно, они обнаружили новые следы, указывающие на существование новых частиц. Другие группы, пытаясь зарегистрировать другие взаимодействия, устанавливали фотопластинки в обсерваториях в Пиренеях и в Андах. Ученые, работающие в Бристоле и Манчестере, тоже обнаружили на своих фотопластинках следы новых частиц. Как оказалось, Раби следовало беспокоиться не о мюонах. На свет явился целый зверинец частиц.
Масса некоторых из них была равна одной восьмой массы протона или нейтрона. Такие частицы, названные пионами, встречались двух видов – с положительным и отрицательным зарядом. Электрически нейтральная разновидность, зарегистрировать которую было труднее, была открыта позже. В Манчестере были получены два снимка из камеры Вильсона, на которых некая нейтральная частица, по-видимому, распадалась на пионы. Масса этой новой частицы была приблизительно равна половине массы протона. В камере, установленной на вершине горы Вилсон, были получены другие свидетельства, подтверждающие открытие таких частиц, названных каонами, которых было найдено четыре вида.
Со временем открывали все новые и новые частицы, так что общая картина стала совершенно неподъемной. В 1955 г. нобелевский лауреат Уиллис Лэмб съязвил в своей благодарственной речи: «Если раньше за открытие новой частицы давали Нобелевскую премию, то теперь за это следовало бы штрафовать на десять тысяч долларов». Когда ученые выяснили, как химические элементы образуются из электронов, протонов и нейтронов, они надеялись упростить периодическую систему. Однако оказалось, что эти три частицы были лишь вершиной айсберга. Теперь обнаружилось более сотни разных частиц, которые, по-видимому, образовывали те кирпичики, из которых состоит материя. Энрико Ферми сказал тогда одному студенту: «Молодой человек, если бы я знал названия всех этих частиц, я был бы ботаником».
Начались поиски объединяющего принципа, который объяснил бы существование мюонов, пионов, каонов и других частиц, – так же как Менделееву удалось найти порядок классификации элементов и логику их расположения в периодической системе.
Основополагающая структура, которая наконец позволила понять логику этого зверинца частиц – так сказать, нарисовать план, позволяющий не заблудиться в зоопарке, – оказалась в итоге математическим объектом.
План зоопарка частиц
Когда пытаешься что-то классифицировать, полезно выделить некую основную характеристику, позволяющую разделить множество неупорядоченных объектов на меньшие группы. Так, идея биологического вида помогла установить некий порядок в животном царстве. В случае физики элементарных частиц одной из важных неизменяемых характеристик, которые позволили разбить весь этот зоопарк на меньшие группы, был электрический заряд. Как та или иная частица взаимодействует с электромагнитным полем? Электроны отклоняются в нем в одну сторону, протоны – в другую, а нейтроны вообще его не замечают.
По мере обнаружения новых частиц их можно было сортировать при помощи электромагнитного поля. Некоторые из них отправлялись в клетку к электрону, другие – к протону, а остальные следовало поместить вместе с нейтроном. Так был сделан первый шаг к упорядочению зверинца частиц.
Но электромагнитное взаимодействие – это лишь одна из четырех известных нам сил, связывающих Вселенную воедино. Три остальные силы – это гравитация, сильное ядерное взаимодействие, которое связывает протоны и нейтроны, удерживая их вместе внутри атомного ядра, и, наконец, слабое ядерное взаимодействие, управляющее такими процессами, как радиоактивный распад.
Задача состояла в выделении других характеристик, которые подобно электрическому заряду могли бы выявить разное поведение этих частиц с точки зрения других фундаментальных взаимодействий. Например, хорошим критерием для установления некоторой иерархии в зоопарке частиц была их масса. По этому признаку можно сгруппировать вместе пионы и каоны, масса которых на порядок меньше, чем у протонов и нейтронов, из которых состоит обычная материя. В другую группу входили вновь открытые сигма-, кси– и лямбда-гипероны, более тяжелые, чем протоны и нейтроны, и часто распадающиеся на протоны и нейтроны.
Частицам с близкой массой часто присваивали одинаковые греческие названия. Собственно говоря, массы протона и нейтрона настолько близки, что их тоже считали родственными частицами, и немецкий физик Вернер Гейзенберг (идеи которого легли в основу нашего следующего «рубежа») придумал для них новое общее название – нуклоны. Но масса все же была грубоватым критерием для классификации частиц. Физики искали чего-то более фундаментального, какой-нибудь закономерности, которая была бы так же эффективна, как и открытый Менделеевым принцип расположения атомов.
Ключевым элементом, позволившим разобраться в этой лавине новых частиц, стало новое свойство, называемое странностью. Название это возникло в связи со странным поведением некоторых из таких частиц при их распаде. Поскольку, в соответствии с уравнением Эйнштейна E = mc2, масса эквивалентна энергии, а природа предпочитает низкоэнергетические состояния, частицы с большей массой часто стремятся распасться на менее массивные частицы.
Существует несколько механизмов такого распада, каждый из которых основан на одном из фундаментальных взаимодействий. Каждый из механизмов имеет свои характерные признаки, что позволяет физикам понять, какое из фундаментальных взаимодействий вызывает данный распад. Наиболее вероятное для распада той или иной частицы взаимодействие также определяется энергетическими соображениями. Сильное ядерное взаимодействие обычно приводит к распаду частицы быстрее всего, в течение 10–24 секунды. Следующим в этой иерархии идет электромагнитное взаимодействие, которое может вызвать испускание фотонов. Слабое ядерное взаимодействие наименее выгодно энергетически, а потому занимает большее время. Распад частицы через слабое ядерное взаимодействие может занять около 10–11 секунды. Таким образом, измеряя время, проходящее до распада, можно выявить признаки участия в нем того или иного взаимодействия.
Например, дельта-барион распадается за 6 · 10–24 секунды на протон и пион через сильное ядерное взаимодействие, а сигма-гиперон распадается на те же протон и пион за 8 · 10–11 секунды. Большее время распада говорит о том, что он происходит с участием слабого ядерного взаимодействия. Между двумя этими случаями мы находим пример нейтрального пиона, распадающегося через электромагнитное взаимодействие на два фотона, что занимает 8,4 · 10–17 секунды.
Представим себе шар, лежащий в ложбине. Если слегка подтолкнуть шар вправо, он перекатится через бугорок и попадет в более глубокую ложбину. Этот путь соответствует сильному ядерному взаимодействию. Слева от шара расположен более высокий бугорок, за которым также лежит состояние с более низкой энергией. Это направление соответствует действию слабого ядерного взаимодействия.
Так почему же дельта-барион находит легкий путь через низкий бугорок, а сигма-гиперон преодолевает дополнительные препятствия? Такое поведение казалось странным. Получалось, что некоторые частицы наталкиваются на некий барьер (обозначенный прерывистой линией), который мешает им попасть в нижнюю ложбину по легкому пути.
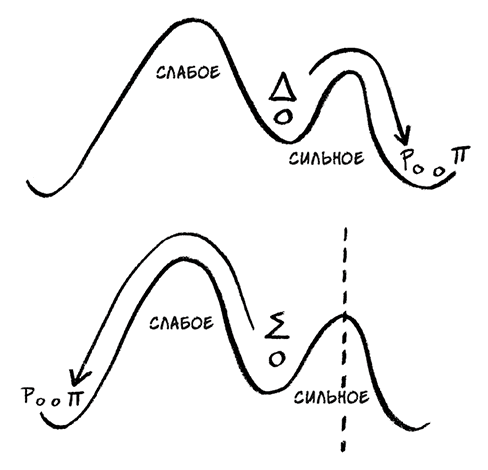
Дельта-барион (Δ) распадается на протон и пион через сильное взаимодействие. В отличие от него сигма-гиперон (Σ) распадается через слабое взаимодействие
Красота должна быть странной
Физики Абрахам Пайс, Мюррей Гелл-Манн и Кадзухико Нисидзима придумали хитроумный способ разрешения этой загадки. Они предложили новое свойство, подобное заряду, которое определяло, могут или не могут такие частицы участвовать в сильном взаимодействии. Такое новое свойство, названное странностью, позволило физикам классифицировать все эти новые частицы. Каждой частице можно было присвоить значение странности в соответствии с тем, проходил или не проходил ее распад по «длинному пути».
Идея состояла в том, что сильное взаимодействие не может изменить странность частицы, так что если две частицы имеют разную странность, то распад одной в другую через сильное взаимодействие невозможен. На пути в нижнюю ложбину стоит барьер. Однако слабое взаимодействие может изменить странность. Поэтому, раз дельта-барион распадается в протон через сильное взаимодействие, обе эти частицы имеют одинаковую странность, равную 0; в то же время сигма-гиперон имеет другое значение странности, так как для его распада в протон необходимо слабое взаимодействие, и ему приписали странность, равную –1. То, что это значение получилось отрицательным, связано только с причудами нумерации разных частиц. Если бы оно было равно 1, а не –1, ничего не изменилось бы.
Затем были обнаружены еще более экзотические частицы, возникающие в высокоэнергетических столкновениях, – они распадались в два этапа. Их назвали каскадными частицами и предположили, что они обладают двойной странностью, то есть имеют странность, равную –2. Результат первого этапа распада имеет странность –1 и распадается на протоны и нейтроны, имеющие нулевую странность. Это несколько похоже на фокус с вытягиванием кролика из шляпы, но он составляет часть научного процесса. В науке то и дело приходится извлекать что-нибудь из шляпы. Большую часть извлеченного приходится отбрасывать, так как она ни на что не годится. Но, если вытаскивать достаточно долго, рано или поздно попадется кролик. Гелл-Манн рассказывал: «Я придумал теорию странности, когда объяснял кому-то одну неправильную идею: я случайно оговорился, и получилась теория странности». Как оказалось, странность была в высшей степени замечательным кроликом.
Исходно понятие странности было введено в качестве бухгалтерского фокуса, приема, который облегчал учет каналов распада из одних частиц в другие. Никто не предполагал, что в идее странности содержится какой бы то ни было физический смысл. Она была нужна, только чтобы установить очередной набор клеток в зоопарке частиц. Но эта новая характеристика оказалась первым намеком на существование гораздо более глубокой физической реальности, действующей под всеми этими частицами. Ключевой момент настал, когда частицы со сходной массой нанесли на график, связывающий значения странности и электрического заряда. Получившаяся картина была преисполнена симметрии.
Частицы расположились по шестиугольной решетке, причем в центральной точке этой решетки находились сразу две частицы. Если пионы и каоны расположить на графике зависимости странности от заряда, то тоже получается сходная структура. Когда получаешь такую конструкцию, это несомненно что-то значит. Ключ к пониманию более глубокой реальности, лежащей за этими частицами, состоял в осознании того, что шестиугольные структуры, которые они образовывали, не были чем-то новым – они встречались и раньше. Не в физике, а в математике симметрии.
Симметричное просветление
Для человека, изучавшего математику симметрии, такая шестиугольная система клеток со сдвоенной точкой в центре выглядит очень знакомо. Она является визитной карточкой вполне конкретного симметричного объекта, называемого группой SU(3).
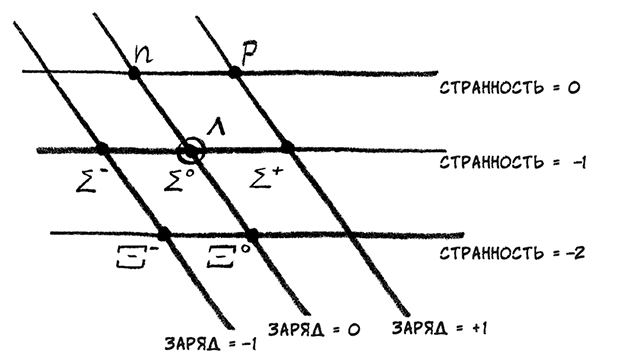
На мой взгляд, это великолепно. Про симметрию я знаю. У меня появляется шанс понять, что происходит в глубинах моей игральной кости. Собственно говоря, моя кость – это идеальное средство объяснения идей, которые лежат в основе математики симметрии. Преобразованиями симметрии такого кубика (если пренебречь очками на его гранях) называются все способы взять кубик, повернуть его и положить обратно так, чтобы он выглядел точно таким же образом, как раньше. Всего таких движений существует 24. Например, кубик можно просто повернуть на четверть оборота вокруг одной из граней или повернуть его на треть оборота вокруг одной из осей, проходящих через противоположные углы кубика.
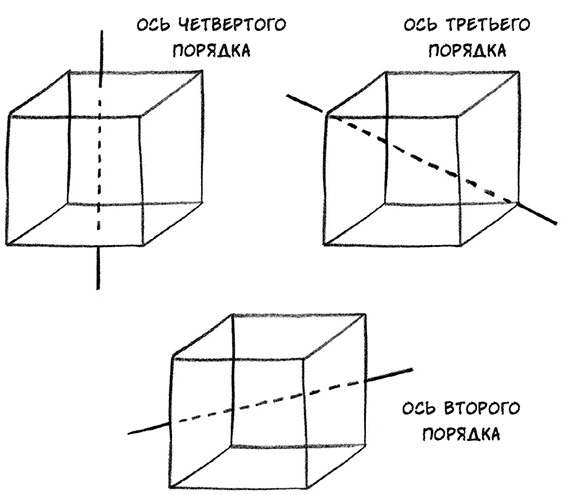
Всего разных вариантов действий существует 24 (включая тот странный вариант, в котором кубик вообще можно оставить в покое и ничего с ним не делать). Этот набор симметричных движений называют S 4 или группой симметрии четвертого порядка. С учетом зеркальной симметрии, то есть того обстоятельства, что кость также можно увидеть в зеркальном отражении, у такого кубика имеется 48 разных симметрий.
Кубик следует рассматривать как геометрическую форму в трехмерном пространстве, на которую воздействует группа симметрии S 4. Но существуют и другие геометрические формы, имеющие те же симметрии. Например, другой трехмерной геометрической формой, группа симметрии которой та же, что и у куба, является октаэдр. Кроме того, существуют объекты более высоких размерностей, также имеющие группу симметрии S 4. Таким образом, имеется много разных геометрических форм, в основе которых лежит одна и та же группа симметрии.
В основе шестиугольной схемы систематизации частиц лежит не группа симметрии игральной кости, а другой симметричный объект, называемый SU(3). Обозначение SU(3) означает «специальная унитарная группа третьего порядка», но такая группа может описывать симметрии разных геометрических объектов разной размерности. Шестиугольная решетка, образованная частицами, совпадает с конструкцией, которую математики используют для описания воздействия SU(3) на объект в восьмимерном пространстве. Восемь частиц, образующих решетку, соответствуют числу измерений, необходимых для создания такого симметричного объекта.
Этот шестиугольник стал тем розеттским камнем, который открыл для физики элементарных частиц совершенно новое направление, хотя для описания этого переворота обычно используют другую культурную аналогию. Путеводный свет этой фигуры с восемью частицами, соответствующей такому восьмимерному представлению, привел к так называемому «восьмеричному пути», название которого цитирует буддистскую идею восьмеричного пути к духовному просветлению.
Существуют и другие фигуры, соответствующие объектам разных размерностей, на которые может воздействовать SU(3). Восхитительное откровение состояло в том, что эти другие схемы можно использовать для расположения других обитателей нашего зверинца частиц. Оказалось, что разные геометрические представления симметрий группы SU(3) отвечают за разные физические частицы, из которых состоит материя Вселенной.
Я не перестаю поражаться тому, как физический мир снова и снова оказывается математическим объектом. Спрашивается, в том ли тут дело, что математика просто дает удобные средства для связного описания физической Вселенной, или же физическая Вселенная на самом деле является физическим проявлением математического объекта? Эта новая связь превратила физические частицы в геометрические элементы, стабилизированные группой симметрии, действующей в геометрическом пространстве.
Гейзенберг был прав, когда писал: «Современная физика определенно признала правоту Платона. Собственно говоря, мельчайшие элементы материи не есть физические объекты в обычном смысле этого слова; они являются формами, идеями, которые можно недвусмысленно выразить только на языке математики». На смену Платоновым икосаэдру воды и тетраэдру огня пришла эта новая странная симметричная форма группы SU(3).
Когда физический мир превращается в математический объект, я немедленно чувствую, что могу его понять. Математика симметрии – это мой язык. Для большинства людей превращение фундаментальных частиц в математические элементы означает отдаление от известных им понятий. Сравнение элементарных частиц с бильярдными шарами или волнами придает этим частицам большую осязаемость. Как можно понять что-либо, если оно не вытекает из нашего опыта физического взаимодействия с окружающим миром? Даже абстрактный язык восьмимерных симметричных объектов возможен лишь как абстрактное расширение идей о вещах, знакомых нам в своей физической форме, таких как симметрия моей игральной кости из Лас-Вегаса.
Многоликая симметрия
Тут важно отметить, что могут существовать несколько разных геометрических объектов, в основе которых лежит одна и та же группа симметрии. И наоборот, если имеется некая группа симметрии, могут существовать несколько разных геометрических объектов, симметрии которых описываются этой группой. Математики говорят, что объект является представлением абстрактной группы симметрии подобно тому, как три яблока или три игральные кости являются физическими проявлениями абстрактной концепции числа 3. Например, если взять все ту же игральную кость, ее можно повернуть 24 различными способами. Рассматривая четыре диагонали, проходящие между противоположными углами кубика, можно сказать, что такие повороты производят перестановки этих диагоналей.
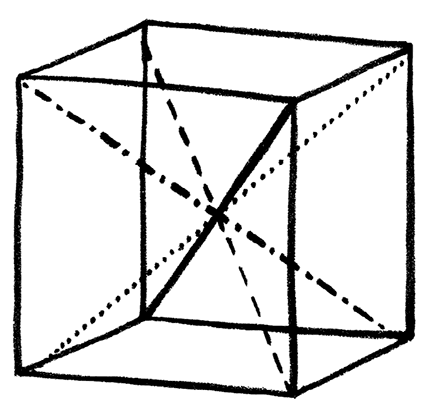
Если поместить на углы кубика четыре игральные карты (туза, короля, даму и валета), то каждый поворот будет перетасовывать эти карты: всего существует 24 разных способа перетасовки четырех карт. Но можно получить и другое физическое представление этой группы симметрии. Возьмем тетраэдр и рассмотрим повороты и отражения этой фигуры: в этом случае также существуют 24 разные симметрии. Если приклеить игральные карты на грани четырехгранной треугольной пирамиды, то симметрии тетраэдра снова дают 24 разных варианта перетасовки этих карт. Эта группа симметрии имеет две разных трехмерных реализации в качестве симметрии геометрического объекта – одна из них включает в себя вращения куба, а другая – вращения и отражения тетраэдра. Оказывается, что если посмотреть на все физические геометрические представления группы SU(3) во всех измерениях, то эти симметричные объекты позволят создать все разнообразие появившихся фундаментальных частиц.
В 1961 г. два физика, Гелл-Манн и Юваль Неэман, независимо друг от друга выявили в этих частицах такие закономерности. При этом Неэман совмещал занятия физикой с карьерой в Силах обороны Израиля и был отправлен в Лондон на должность военного атташе. Сначала он собирался изучать общую теорию относительности в Кингс-колледже, но, поняв, что тот находится в нескольких милях от посольства Израиля, расположенного в Кенсингтоне, решил разузнать, чем занимаются по соседству, в Имперском колледже. Там занимались физикой элементарных частиц. Так Неэман переключился с предельно большого на предельно малое.
Хотя схема, составленная для частиц лямбда, сигма и кси, при добавлении протона и нейтрона соответствовала восьмимерной симметрии SU(3), в аналогичной схеме для каонов и пионов не хватало частицы, которая должна была быть в ее центре. Либо схема была ошибочной, либо существовала еще неоткрытая частица. Гелл-Манн опубликовал свое предсказание существования такой частицы в препринте Калтеха в 1961 г. И всего несколько месяцев спустя физики из Беркли благополучно открыли эта-мезон.
Для новой теории это идеальный вариант развития событий. Если теория делает физическое предсказание, которое затем подтверждается, можно быть уверенным, что ставка сделана правильно. Та же история повторилась, когда и Гелл-Манн, и Неэман были в 1962 г. на конференции в ЦЕРН. На этой конференции было объявлено об открытии множества новых частиц – трех Σ*-гиперонов со странностью –1 и двух Ξ*-гиперонов со странностью –2. Предполагалось, что эти частицы должны соответствовать одной из схем, иллюстрирующих действие группы симметрии SU(3) на симметричный объект в более высоких измерениях.
Гелл-Манн и Неэман независимо друг от друга сидели на лекции, пытаясь встроить эти новые частицы в свои схемы, когда у обоих начала проявляться другая картинка, соответствующая еще одному симметричному объекту, на котором действует группа SU(3), – объекту десятимерному. Но один из углов схемы оставался незаполненным. Частиц было всего девять. Гелл-Манн и Неэман одновременно осознали, что одна позиция в схеме пустует, из чего следовало предсказание существования новой частицы. Первым поднял руку Гелл-Манн, который и предсказал омега-гиперон со странностью –3. Это предсказание было подтверждено в январе 1964 г.
История периодической системы Менделеева заново повторилась в XX в.: основополагающая закономерность была выявлена, но в головоломке не хватало некоторых элементов. Подобно тому как открытие недостающих атомов придало убедительности модели Менделеева, открытие этих недостающих частиц помогло убедить физиков в том, что эти математические схемы являются могущественным средством ориентации в зоопарке частиц.
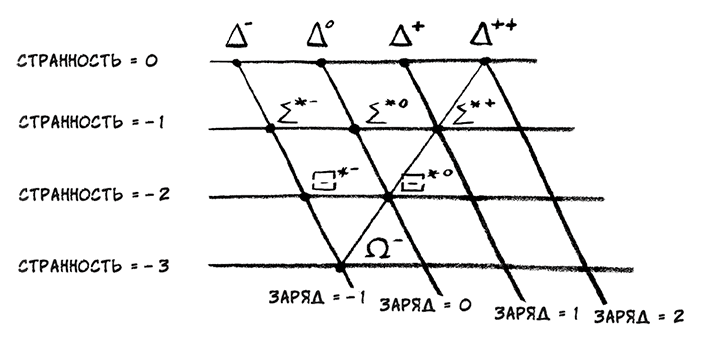
Закономерности, открытые Менделеевым в периодической системе, оказались следствием того, что атомы элементов состоят из фундаментальных ингредиентов – протонов, электронов и нейтронов. Существовало ощущение, что закономерности, найденные во всех этих вновь открытых частицах, намекают на нечто похожее – на существование в основе сотен зарегистрированных частиц еще более фундаментальных кирпичиков.
Кварки – недостающий последний уровень?
Некоторые физики заметили, что если расположить схемы, соответствующие разным многомерным представлениям SU(3), послойно, получается конструкция в форме пирамиды, у которой отсутствует самый верхний слой. На вершине всего этого должно быть что-то похожее на простой треугольник. Такой треугольник соответствовал бы простейшему физическому представлению SU(3), действующему в трехмерной геометрии. Если посмотреть на эти слои с точки зрения симметрии, видно, что именно из недостающего слоя можно было бы получить все остальные слои. Но никто никогда не видел никаких частиц, которые соответствовали бы этому недостающему слою.
Среди тех, кто догадывался, что такой дополнительный уровень может предполагать три фундаментальные частицы, из которых могут быть построены все частицы, соответствующие следующим уровням, был Роберт Сербер, бывший правой рукой Оппенгеймера в «Манхэттенском проекте». В 1963 г. за обедом Сербер рассказал об этой идее Гелл-Манну, но, когда Гелл-Манн спросил его, какой электрический заряд могли бы иметь эти гипотетические частицы, Сербер затруднился с ответом. Гелл-Манн начал писать на салфетке и вскоре получил ответ. Их заряд должен быть равен 2/3 или –1/3 заряда протона. Такой ответ казался бессмысленным. «Странный был бы выверт», – заметил Гелл-Манн. Никаких объектов, заряд которых не был бы равен целому числу зарядов электрона или протона, в истории физики никогда не наблюдалось.
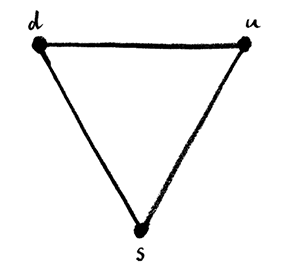
Треугольник, предполагающий существование трех новых частиц: верхнего, или u-кварка, нижнего, или d-кварка, и странного, или s-кварка
Ситуация напоминала времена Пифагора. Считалось, что все состоит из целых чисел, как вдруг появилось нечто, что, по-видимому, делило эту фундаментальную единицу на части. Дроби задавались отношениями целых чисел, но до сих пор никто никогда не встречал таких дробных зарядов. Сначала Гелл-Манн отнесся к таким гипотетическим частицам с дробным зарядом скептически, но к вечеру они начали ему нравиться. В последующие недели он стал исследовать возможные следствия этой идеи, называя такие частицы «кворками» – это словечко он использовал и раньше в смысле «непонятные штучки». Сербер считает, что Гелл-Манн обыгрывал в нем тот странный выверт, «quirk», о котором он говорил за обедом.
Читая экспериментальный роман Джеймса Джойса «Поминки по Финнегану», Гелл-Манн набрел на отрывок, определивший правописание слова, которое он стал использовать для обозначения этих гипотетических частиц. Его внимание привлекла первая строчка стихотворения, высмеивающего короля Марка, обманутого мужа, в легенде о Тристане и Изольде: «Three quarks for Muster Mark!»
С учетом того, что таких гипотетических частиц, из которых можно построить другие слои, было три, аналогия казалась точной. Единственная трудность заключалась в том, что Джойс явно считал, что слово «quark» должно рифмоваться с именем «Марк», а не со словом «кворк». Тем не менее утвердились именно те правописание и произношение, которые понравились Гелл-Манну.
В конце концов такие кварки составили последний, по нашим представлениям, уровень устройства материи. Но идея эта прижилась не сразу. Когда Гелл-Манн говорил о кварках по телефону со своим бывшим научным руководителем, тот перебил его: «Мюррей, хватит шутить. Мы же разговариваем по международной связи».
С точки зрения Гелл-Манна, система казалась слишком красивой, чтобы не содержать в себе хотя бы какой-то истины. Идея заключалась в том, что под всеми этими слоями частиц лежит еще один уровень из трех фундаментальных частиц – верхнего кварка, нижнего кварка и странного кварка, заряды которых равны, соответственно, 2/3, –1/3 и –1/3. Остальные частицы образованы из сочетаний этих кварков (и их античастиц, как в случае каонов и пионов). Число странных кварков, использованных в конструкции частицы, определяет ее странность. Таким образом, схему восьмеричного пути, состоящую из протона, нейтрона и сигма-, кси– и лямбда-гиперонов, теперь можно перерисовать с учетом таких кварковых ингредиентов.
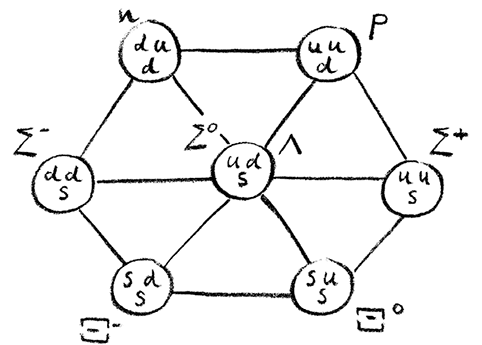
Кварковые составляющие восьмеричного пути
При каждом шаге вверх по этой схеме число странных кварков уменьшается на единицу. Если двигаться в направлении увеличения заряда, то на каждом шаге увеличивается число верхних кварков, имеющих заряд 2/3. Существует еще и третье направление, которое определяет увеличение числа нижних кварков. Схожие закономерности существуют и в других слоях частиц.
Идею разборки материи на такие более мелкие частицы обдумывал не только Гелл-Манн. Американский физик Джордж Цвейг тоже полагал, что эти схемы указывают на существование более фундаментального уровня частиц. Он называл их тузами, но при этом он, вероятно, в большей степени, чем Сербер или Гелл-Манн, верил в физическую реальность таких частиц. Руководитель теоретического отдела ЦЕРН посчитал его препринты, в которых он излагал свои мысли, «полной чушью». Даже Гелл-Манн, высказывавший схожие идеи, считал их всего лишь математической моделью, позволяющей внести в схемы некий согласованный порядок. Для него они были мнемоническим приемом, а не реальными объектами. Гелл-Манн не соглашался с Цвейгом, верившим в физическую реальность кварков: «Модель реальных кварков – это для тупиц!»
От фантазии к реальности
Все это изменилось в конце 1960-х гг. благодаря результатам, полученным в экспериментах в Стэнфордском центре линейного ускорителя, в которых протоны бомбардировали электронами. В соответствии с анализом заряда протона предполагалось, что его размеры должны составлять порядка 10–15 м. Считалось, что протон должен быть однородно распределен по этой малой области. Однако, когда на сгусток протонов направили электроны, экспериментаторы были поражены полученной картиной рассеяния. Как и в случае удививших Резерфорда результатов бомбардировки атомов золота альфа-частицами, оказалось, что протон, как и атом, в основном состоит из пустого пространства.
Картина рассеяния соответствовала протону, состоящему из трех частиц меньшего размера. Как и в опытах Резерфорда, какой-нибудь электрон время от времени точно попадал в одну из этих трех точек и отражался обратно, в направлении источника электронов. Эксперимент, по-видимому, подтверждал представление о протоне, состоящем из трех кварков. Хотя никто никогда не видел отдельного кварка, картина рассеяния электронов указывала на то, что три более мелкие частицы, из которых образован протон, действительно существуют.
Выяснилось, что тупицы были правы. Верхний, нижний и странный кварки оказались не просто математическими фокусами, но элементами физической реальности. Затем выяснилось, что этих трех кварков недостаточно для всех новых частиц, и в конце концов у нас оказалось шесть кварков и соответствующие им античастицы. В дополнение к трем кваркам, окрещенным Гелл-Манном, появились еще три: очарованный кварк, истинный кварк и прелестный кварк.
Открытие этого способа упорядочения зверинца физических частиц при помощи математики симметрии стало одним из самых захватывающих открытий ХХ в. Увидеть, как все эти фундаментальные частицы выстраиваются в готовые схемы, уже существовавшие в математике симметрии, наверное, было совершенно восхитительно. Если бы я выбирал, какое физическое открытие хотел бы совершить, это открытие имело бы хорошие шансы на победу. Мне кажется, это было похоже на ощущения археолога, который находит узор, до сих пор встречавшийся только на другом конце света. Когда обнаруживаешь такие характерные узоры, становится очевидно, что между этими двумя культурами должна существовать какая-то связь.
Странная особенность этой пирамиды из треугольников и шестиугольников, соответствующих различным представлениям группы SU(3), заключается в том, что она продолжается до бесконечности, из чего следует, что, склеивая вместе все больше и больше кварков, можно получать все новые и новые экзотические частицы. Физическая модель, по-видимому, заканчивается на уровне, в котором располагаются частицы, собранные из трех кварков. Однако в 2015 г. появились волнующие сообщения об обнаружении на LHC свидетельств существования частицы, состоящей из пяти кварков. Исследователи из ЦЕРН чуть не упустили эту частицу, которую назвали пентакварком, приняв ее за фоновый шум. Но, когда они попытались удалить этот шум, они обнаружили мощный сигнал, указывающий на следующий уровень пирамиды симметрий. Как сказал один из ученых, работающих в ЦЕРН: «Мы не искали пентакварк. Это он нас нашел».
До каких пределов мы можем углубляться в математику в поисках предсказаний того, что еще можно увидеть на LHC? Например, существует ли еще более крупный симметричный объект под названием SU(6), который может объединить все шесть кварков – верхний, нижний, странный, очарованный, истинный и прелестный – в множество потрясающих частиц. Тогда вместо двумерной схемы, в которой мы распределяли частицы по семействам, понадобилась бы схема пятимерная. Хотя создание некоторых из таких более экзотических комбинаций кварков и представляется возможным, различия между массами кварков становятся все больше, что приводит к нарушению прекрасной математической симметрии и делает реальное существование таких частиц все менее вероятным. Например, t-кварк настолько нестабилен, что распадается, даже не успев соединиться с каким-нибудь другим кварком. Физики не могут ответить на вопрос о причинах таких различий между массами кварков – то есть пока не могут. Математика, по-видимому, предлагает гораздо большее разнообразие частиц, чем может выдержать физическая реальность. Реальность кажется лишь бледной тенью математических возможностей. Однако понимание даже этой реальности по-прежнему остается непростым делом.
Я должен признать, что, даже имея в своем распоряжении математический аппарат, на разработку которого я потратил многие годы, я не уверен, что действительно понимаю, что такое кварки. Я провожу целые месяцы за изучением книг по физике элементарных частиц, таких как «Квантовая механика и частицы природы» Энтони Садбери, и конспектов лекций оксфордских курсов по симметрии и физике элементарных частиц. И вот, сидя тут в окружении всех этих историй о внутреннем устройстве моей игральной кости, я понемногу начинаю впадать в отчаяние. Того, чего я все еще не знаю, так много: интегралы по путям, описывающие будущее частиц, внутреннее устройство уравнений Клейна – Гордона, точный смысл диаграмм Фейнмана, которые физики с такой легкостью рисуют на доске… Я с завистью смотрю на своего сына, который только начинает изучать физику. У него будет время погрузиться в этот мир, узнать все это так же близко, как я знаю область своей работы.
То же и с виолончелью. Я взрослый человек и хочу играть сюиты Баха сейчас, а не через десять лет. Но обучение трубе заняло у меня годы, и только медленная, постепенная, настойчивая учеба может вывести меня на тот уровень, на котором я смогу играть эти сюиты. По крайней мере, в этом месяце мне наконец удалось сдать экзамены за третий класс. Я сам удивился, как я нервничал. Смычок трясся у меня в руках. И хотя вокруг меня были сплошные одиннадцатилетки, ждавшие своего экзамена по блок-флейте за первый класс, чувство успеха все равно было очень приятным.
Я знаю, что, как и в случае с виолончелью, если я проведу достаточно долгое время в мире физики элементарных частиц, у меня есть надежда узнать кое-что из того, чем мои коллеги с физического факультета в соседнем корпусе живут изо дня в день. Меня пугает сознание того, что мне не хватит времени узнать все. Но даже те физики, которые с такой завидной для меня легкостью играют с нашим современным уровнем знаний, признаю́т, что никогда не смогут точно знать, что знают всё.
Ковбои и кварки
Чтобы узнать, думают ли специалисты в области физики элементарных частиц, что известная нам сегодня кварковая головоломка может быть составлена из еще более мелких кусочков, я договорился о встрече с одной из тех, кто открыл один из последних фрагментов этой головоломки. Мелисса Франклин, ставшая сейчас профессором в Гарварде, была одним из участников группы, которая обнаружила t-кварк в эксперименте, проведенном в Фермилаб. В противоположность распространенному мнению открытие частицы – это не момент озарения, а долгий и медленный процесс. Но Франклин считает, что так даже лучше: «Если бы это был просто “бум!”, было бы неинтересно. Тратишь 15 лет на строительство машины, а потом вдруг бум! – и все кончено? Ужас». Сбор данных, начатый в 1994 г., занял около года, и только в 1995-м исследовательская группа решила, что получено достаточно доказательств, чтобы уверенно подтвердить открытие этой частицы, предсказанной математиками.
Франклин определенно находится с экспериментальной, а не с теоретической стороны границы, разделяющей физиков. Она предпочитает работать дрелью, а не карандашом и участвовала в сооружении детектора в Фермилаб с начала и до конца.
Мы оба выступали с докладами на Римском фестивале науки, посвященном теме непознаваемого, поэтому договорились встретиться в холле той довольно странной гостиницы, оформленной по мотивам игры в поло, в которой мы жили. Поскольку Франклин расхаживает у себя на работе в ковбойских сапогах, я предположил, что ей, может быть, уютнее находиться в этой гостинице, покрытой изображениями лошадей, чем мне.
Однако ее появление было чрезвычайно драматичным: первым делом она упала с лестницы, ведущей в холл. Отряхнувшись, она как ни в чем не бывало подошла ко мне и села.
Мне очень хотелось узнать, думает ли она, что кварки – это последний уровень, или же под этими частицами, в открытии которых она принимала участие, могут скрываться другие структуры.
«Мы дошли до масштаба 10–18 метра. Следующие семь или восемь порядков величины изучать довольно трудно. Но там конечно же много чего может случиться. Странно думать, что я могу умереть до того – особенно если я и дальше буду падать с лестниц, – что я могу умереть еще до того, как мы продвинемся дальше».
Я спросил, могут ли существовать фундаментальные ограничения того, что мы можем знать.
«Точно есть пределы, которые не будут преодолены при моей жизни, но я не уверена, есть ли другие ограничения. Когда в экспериментальной физике говорят, что чего-то никак нельзя сделать, это лучший способ устроить так, чтобы кто-нибудь придумал, как это можно сделать. В течение моей жизни я никогда не смогу измерить что-то, распадающееся за 10–22 секунды. Я не думаю, что это возможно. Но это не значит, что можно доказать, что это в принципе непознаваемо.
Раньше мы не могли себе представить лазер или атомные часы, да? Я думаю, что все ограничения в физике будут атомными, потому что все, что мы делаем, связано с атомами. Я понимаю, это звучит странно, но в детекторе должны быть атомы».
Интересно, как Эйнштейн вывел существование атомов из наблюдения того, как они воздействуют на что-то видимое – на зерна пыльцы или на угольную пыль. А сегодня мы знаем о существовании кварков по тому, как частицы отражаются от протонов. Так что, возможно, существуют способы заглянуть еще глубже.
«Я уверена, что Гейзенберг или Бор и представить себе не могли то, что мы сегодня можем измерить. Наверное, то же самое можно будет сказать и о нашем поколении… хотя мы-то, конечно, гораздо умнее», – смеется она.
Мне кажется, что эта проблема встает перед каждым поколением. Как можно знать заранее, какие хитрые новые методы можно придумать, чтобы копнуть ткань Вселенной еще немножко глубже? Но Франклин интересует еще и другой вопрос: какую часть того, что уже содержится в данных, получаемых из детекторов нынешнего поколения, мы не замечаем?
«Многие молодые ученые, работающие в моей области, не верят, что можно найти что-то новое, не предсказанное теоретиками. Это очень грустно. Когда мы натыкаемся на что-то, что не было предсказано теорией, мы чаще всего считаем, что это ошибка, и отбрасываем такой результат как флуктуацию. Это меня беспокоит, потому что наши эксперименты устроены таким образом, что там есть триггеры, которые срабатывают на определенные вещи – но только на те вещи, которые мы ищем, а не на другие. Интересно, что мы при этом пропускаем».
Такая судьба, видимо, чуть не постигла пентакварк, об открытии которого недавно объявили в ЦЕРН. Его чуть не посчитали шумом. Поскольку я писал книгу о том, чего мы знать не можем, Франклин спросила меня, согласился бы я узнать все, если бы это можно было сделать одним нажатием кнопки. И когда я уже протянул руку к ее гипотетической кнопке, чтобы продать душу дьяволу за знание доказательств всех теорем, над которыми я работаю, она меня остановила.
– Я бы этого не делала.
– Почему?
– Потому что так неинтересно. То есть существуют какие-то вещи: если бы я могла нажать на кнопку и тут же бегло заговорить по-итальянски, я бы нажала. Но не в науке. Мне кажется, дело в том, что так на самом деле нельзя ничего понять. Нужно приложить усилия. Нужно пытаться что-то измерить, стараться что-то понять.
Я был заинтригован. Неужели она не нажала бы на кнопку, если бы могла узнать, существуют ли за кварками другие частицы?
– Если бы мне просто объяснили методику, это было бы здорово. Но одна из главных причин, по которым мы вообще занимаемся наукой, – это появление новых идей. Бороться за знания интереснее. Так что с кнопкой все не так просто.
Мне кажется, что Франклин просто нравится делать новые вещи, искать новые частицы, управляя погрузчиками и сверля дырки в бетоне, а не размышлять за письменным столом.
– Экспериментаторы кое в чем похожи на ковбоев. Зааркань-ка вон ту штуку и тащи ее сюда. И не обращай внимания на того парня, который сидит в углу и о чем-то там думает. Когда мне будет 60, я стану менее категоричной и предубежденной. Уйду из ковбоев… Нет, не хочу уходить из ковбоев… Не знаю… Это трудно. Ковбои не так-то просты. Ходить на работу в ковбойских сапогах – это своего рода позиция.
С этими словами она села в такси и укатила в римский закат, навстречу новым научным приключениям, в поисках знаний, которые можно было бы заарканить.
Виолончель или труба?
В самом ли деле кварки, в открытии которых участвовала Франклин, образуют самый последний рубеж, или же когда-нибудь их можно будет разделить на меньшие части подобно тому, как атом разделили на электроны, протоны и нейтроны, а их, в свою очередь, – на кварки?
Многим физикам кажется, что имеющиеся сейчас экспериментальные данные в сочетании с математической теорией, которая обосновывает эти эксперименты, дают нам ответ на вопрос о сущности действительно неделимых частиц, из которых состоит игральная кость. Как все 118 элементов периодической системы могут быть сведены к различным комбинациям базовых структурных элементов трех видов – электронов, протонов и нейтронов, – так и сотни новых частиц, обнаруженных в столкновениях космических лучей, могут быть сведены к простому набору ингредиентов. Дикое разнообразие зверинца частиц укрощено. Но насколько можно быть уверенным в том, что его ворота не откроются снова и из них не появятся новые звери? По правде говоря, физики не знают, закончена ли эта история.
В симметрической модели, лежащей в основе систематизации этих частиц, треугольник, соответствующий кваркам, является последним неделимым слоем из всех, описывающих различные физические представления группы SU(3). Математика симметрии предполагает, что мы достигли дна. Треугольник, соответствующий кваркам, образует неделимый слой, из которого образуются все остальные слои. То есть математика симметрии говорит нам, что мы добрались до неделимого. И все же не повторяем ли мы ошибку Гелл-Манна, отвергшего сперва идею кварков на том основании, что они имеют дробный заряд? Однако у кварков и электронов есть еще одна характеристика, которая до некоторой степени обосновывает веру в их неделимость: они, по-видимому, не имеют объема, но ведут себя так, как если бы они были сосредоточены в одной точке.
С точки зрения математики геометрические формы образуются трехмерными телами, двумерными плоскостями, одномерными прямыми и ноль-мерными точками. Странность заключается в том, что все они были задуманы как абстрактные объекты, не имеющие физического воплощения в нашем трехмерном мире. Действительно, что такое прямая линия? Если провести линию на бумаге и посмотреть на нее под микроскопом, можно увидеть, что она имеет некоторую ширину. То есть на самом деле это не прямая. Собственно говоря, она имеет еще и некоторую высоту, потому что атомы, нанесенные карандашом на бумагу, образуют на ней маленький графитовый (или из чего там сейчас делают карандаши) хребет.
Точно так же точку в пространстве можно определить ее координатами GPS, но никто не ожидает, что какой-нибудь объект будет расположен только в этой точке и нигде больше. Точку нельзя увидеть. Ее размеры равны нулю. И тем не менее электрон во многих отношениях ведет себя так, как если бы он был сосредоточен в единственной точке пространства, и так же ведут себя кварки внутри протона и нейтрона. Картина рассеяния электронов на электронах, а также на кварках внутри протонов и нейтронов имеет смысл только в модели, в которой эти частицы не имеют объема. Если придать им объем, рассеяние будет выглядеть по-другому. А если они действительно являются точечными частицами, трудно ожидать, что они могут быть разобраны на части.
Но тогда как быть с массой электрона? Чему равна плотность электрона? Отношению его массы к объему. Объем равен нулю. Результат деления на ноль равен бесконечности. Бесконечности? Что же, каждый электрон есть маленькая черная дыра? Тут мы полностью переходим на территорию квантового мира, поскольку, как мы увидим на следующем «рубеже», ответить на вопрос о том, где находится частица, оказывается не так легко, как можно было бы ожидать.
Значит ли это, что дискретные ноты трубы победили непрерывное глиссандо виолончели? Очень трудно выяснить, закончилась ли эта история. Атомы считались неделимыми из-за неделимости целых чисел, которые управляли их возможными сочетаниями. И все же в конце концов они распались на мелкие части, которые и составляют наше современное представление о строении Вселенной. Почему же не предположить, что, по мере того как мы копаем глубже и глубже, история будет повторяться и преподносить нам все новые и новые сюрпризы? Почему вообще должно существовать какое-то начало, первый уровень, из которого сделаны все остальные? Это классическая проблема бесконечной регрессии, с которой мы еще не раз встретимся. Как сказала однажды одна пожилая дама ученому, высмеивавшему ее теорию о том, что мир покоится на спине черепахи: «Вы очень, очень умный молодой человек, но только там одна черепаха на другой – и так до самого конца!»
Даже если электроны и кварки – это частицы, каждая из которых сосредоточена в единственной точке пространства, нет причин, по которым точка не могла бы состоять из двух точек и ее нельзя было бы растянуть на части. А может быть, существуют скрытые измерения, с которыми мы еще не умеем взаимодействовать? Таково предположение теории струн. В ней считается, что точечные частицы на самом деле представляют собой одномерные струны, вибрирующие на резонансных частотах, причем разные частоты создают разные частицы. Кажется, что мы описали полный круг и вернулись к Пифагоровой модели мира. Возможно, виолончель все-таки побеждает трубу, а фундаментальные частицы – это на самом деле просто вибрирующие струны.
Если задаться поисками того, чего мы никогда не сможем узнать, то вопрос о том, из чего состоит игральная кость, вполне можно отнести к этой категории. История того, что мы знаем об этой кости, полна предостережений. Окажемся ли мы когда-нибудь в положении, в котором не останется неоткрытых уровней реальности? Сможем ли мы когда-нибудь узнать, что наша новейшая теория – это последняя теория?
Тут, однако, может возникнуть еще одна трудность. Современная теория предельно малого – квантовая физика – утверждает, что в теории имеются неустранимые пределы познания. Как будет показано на следующем «рубеже», пытаясь разделить игральную кость на все более мелкие части, в некоторый момент мы натыкаемся на барьер, который не можем преодолеть.
Назад: 3
Дальше: Рубеж третий: Банка урана

