Эта математическая загадка оставалась нерешенной больше 100 лет. Правда ли, что любая простая (без самопересечений) замкнутая кривая на плоскости содержит четыре точки, представляющие собой углы квадрата с ненулевой стороной?

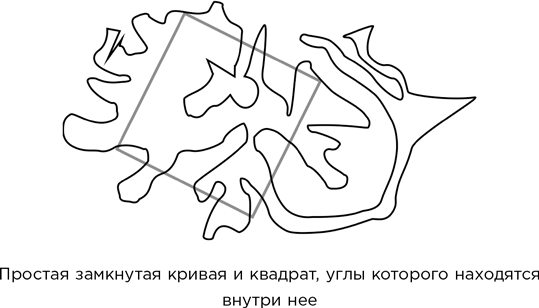
Под «кривой» здесь подразумевается непрерывная линия без разрывов, не обязательно гладкая. Она может иметь острые углы и вообще может быть бесконечно извилистой. Мы настаиваем на ненулевой стороне квадрата, чтобы избежать тривиального ответа, когда одна и та же точка представляет все четыре угла.

Первое печатное упоминание о задаче с квадратным колышком появилось в 1911 г. в ходе конференции на семинаре, который проводил Отто Тёплиц; судя по всему, было обещано доказательство. Однако никакого доказательства опубликовано не было. В 1913 г. Арнольд Эмч доказал, что это утверждение верно для гладких выпуклых кривых, но добавил, что услышал о задаче не от Тёплица, а от Обри Кемпнера. Это утверждение было доказано для выпуклых кривых, аналитических кривых (определяемых сходящимися степенными рядами), достаточно гладких кривых, кривых с симметрией, звездчатых дважды дифференцируемых кривых, пересекающих любую окружность в четырех точках…

В общем, вы поняли. Множество технических гипотез, но никакого общего доказательства и никаких контрпримеров. Может быть, да, может быть, нет. Кто знает?

Существуют обобщения. В Задаче о прямоугольном колышке спрашивается, действительно ли для любого действительного числа r³ 1 любая гладкая простая замкнутая кривая на плоскости содержит четыре вершины прямоугольника с отношением сторон r: 1. Доказан только случай квадратного колышка (r = 1). Существуют также несколько расширений на более высокие размерности при очень сильных ограничениях.