В 1974 г. Ричард Уилсон обобщил «пятнашки» и доказал замечательную теорему. Он заменил сдвижные квадратики сетью. Квадратики здесь представлены числами, которые могут скользить по ребру, если оно соединено с узлом, на котором в данный момент располагается пустой квадратик. При этом пустой квадратик перемещается на новую позицию. Приведенная на рисунке фигура показывает начальное расположение блоков головоломки. Узлы связаны, если соответствующие им квадратики располагаются по соседству.

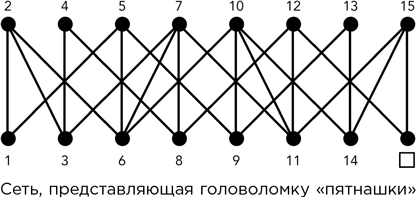
Идея Уилсона состоит в том, чтобы заменить эту сеть вообще любой связанной сетью. Предположим, в ней n + 1 узлов. Первоначально один из узлов, отмеченный квадратиком, считается пустым (назовем его узлом 0), а остальные пронумерованы номерами от 1 до n. Смысл головоломки в том, чтобы двигать эти числа (номера) по сети, меняя местами 0 с номером одного из прилегающих узлов. Правилами оговаривается, что в конце концов 0 вновь должен оказаться в начальной точке. Остальные n чисел могут быть расставлены по сети n! способами. Уилсон задал вопрос: какая доля этих способов может быть получена посредством разрешенных ходов? Ответ, очевидно, зависит от сети, но в меньшей степени, чем можно было бы предположить.

Существует один очевидный класс сетей, для которых ответ оказывается необычно маленьким. Если узлы образуют замкнутое кольцо, то единственное положение, которое можно получить разрешенными ходами, – это начальное положение, поскольку 0 по условию должен вернуться в начальную точку. Все остальные числа будут расставлены в прежнем циклическом порядке; не существует способа, посредством которого один номер может обогнуть другой и оказаться с другой его стороны. Теорема Рика Уилсона (названная так, чтобы избежать путаницы с другим математическим Уилсоном) утверждает, что если оставить в стороне кольцевые сети, то в любой другой сети могут быть получены либо все перестановки без исключения, либо ровно половина (только четные).

Ровно за одним замечательным исключением.

В теореме содержится сюрприз. Уникальный сюрприз: сеть с семью узлами. Шесть из них образуют шестиугольник, а один располагается посередине, на одном из диаметров. В этой сети возможно 6! = 720 перестановок; соответственно, половина равна 360. Но в реальности получить можно только 120.

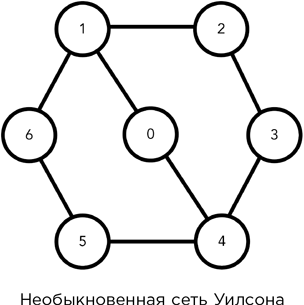
В рассуждениях используется абстрактная алгебра, а именно некоторые элегантные свойства групп перестановок. Подробности см.: Alex Fink and Richard Guy, Rick's tricky six puzzle: S5 sits specially in S6, Mathematics Magazine 82 (2009) 83–102.