Эта старая головоломка – моя любимая, она никогда не надоедает. Это увлекательное занятие, где маленькая математическая догадка могла бы избавить нас от невероятного количества напрасных усилий. Плюс к тому она нужна мне в качестве подготовки к следующей теме.

В 1880 г. нью-йоркский почтмейстер по имени Ной Палмер Чепмэн предложил головоломку, которую он назвал «драгоценной», а дантист Чарльз Певи предложил денежный приз за ее решение. Головоломка ненадолго вошла в моду, но никто не сумел выиграть приз, так что ажиотаж быстро спал. Американский составитель головоломок Сэм Лойд утверждал, что именно он ввел моду на эту головоломку в 1870-е гг., но на самом деле все, что он сделал, – это написал о ней в 1896 г. и предложил приз в $1000 за решение, что на время воскресило интерес к полузабытой игре.

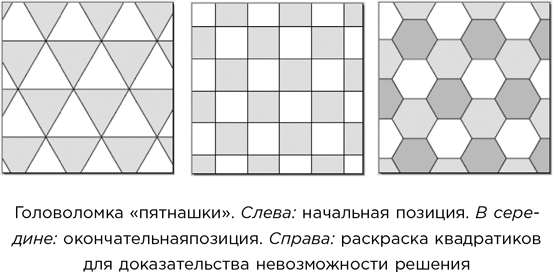
Головоломка «пятнашки» (ее также называют игрой в «15» и «загадочным квадратом») начинается с 15 подвижных квадратиков, пронумерованных числами от 1 до 15 и расставленных в форме квадрата с одним пустым квадратиком в правом нижнем углу. Квадратики расставлены в порядке возрастания, за исключением номеров 14 и 15. Задача играющего – поменять местами квадратики 14 и 15, сохранив положение остальных квадратиков неизменным. Делать это нужно сдвиганием любого из соседних квадратиков на пустое место, причем повторять эту операцию можно сколько угодно.

По мере того как вы сдвигаете все больше и больше квадратиков, номера перепутываются. Но если вы будете действовать аккуратно, вы сможете вновь их распутать. Легко предположить, что при достаточной сообразительности можно получить любое, абсолютно произвольное расположение квадратиков.

Лойд с радостью предложил такой щедрый по тем временам приз, поскольку был уверен, что платить не придется. В игре существует 16! потенциально возможных перестановок (15 нумерованных квадратиков плюс один пустой). Вопрос в следующем: какие из этих вариантов можно получить при помощи серии разрешенных ходов? В 1879 г. Уильям Джонсон и Уильям Стори доказали, что ответ состоит в том, что получить можно ровно половину вариантов; причем (так мы и знали, не правда ли?) вариант, который нужен для получения приза, относится к другой половине. «Пятнашка» нерешаема. Но люди в большинстве своем этого не знали.

Для доказательства невозможности решения нужно раскрасить квадратики под шахматную доску, как на правом рисунке. Сдвиг любого квадратика, по существу, меняет его местами с пустым квадратиком, и всякий раз при этом меняется цвет, связанный с пустым квадратиком. Поскольку в результате пустой квадратик должен вернуться на свое первоначальное место, число шагов должно быть четным. Вообще, любая расстановка может быть получена путем серии обменов, но некоторые комбинации требуют четного числа обменов, а некоторые – нечетного.

Существует множество способов получить любую заданную расстановку, но они либо все четные, либо все нечетные. Желаемый результат может быть получен при помощи всего лишь одной замены (нужно поменять местами 14 и 15), но единица – число нечетное, так что получить такую расстановку четным числом замен невозможно.

Это условие оказывается единственным препятствием: разрешенные ходы позволяют получить ровным счетом половину из 16! возможных расстановок. 16!/2 = 10 461 394 944 000; это число настолько велико, что, сколько бы раз вы ни пробовали, бо́льшая часть вариантов останется неисследованной. Это может заронить в ваше сознание мысль, что возможен, безусловно, любой вариант расстановки.