Я нередко поражаюсь способности Сомса находить закономерности в самых неподходящих для этого обстоятельствах. Невозможно подобрать лучшего примера, чем история, имевшая место ранней весной 1877 г.

Когда, направляясь к дому Сомса, я проходил через Равносторонний парк, на дорожках плясали пестрые пятна света и теней, которые свежеотчеканенное солнышко бросало сквозь кружевные пухлые облака, а живые изгороди звенели птичьими песнями. В такой великолепный день казалось просто неприличным оставаться дома, но все мои усилия оторвать моего друга от каталогизации полной коллекции использованных спичек встретили с его стороны лишь равнодушие.

– Нередко исход дела зависит от того, сколько времени горела спичка, Ватсап, – недовольно проворчал он, занося в блокнот какой-то очередной размер, снятый с циркуля.

Разочарованный, я раскрыл газету на спортивной странице, и мой глаз сразу же выхватил своевременное напоминание о событии, которое даже Сомс вряд ли хотел бы пропустить. У меня же оно совершенно выскочило из головы, вытесненное жужжанием пчел и цветением деревьев. Меньше чем через час мы уже сидели на берегу реки с корзинкой ленча и несколькими бутылками вполне приличного бургундского и ждали начала ежегодной гонки.

– За кого вы болеете, Сомс?

Он прекратил измерение длины сгоревшей части раннешотландской безопасной спички – Сомс настоял на том, чтобы взять некоторое количество спичек с собой, чтобы было чем заняться.

– За голубых.

– Темных или светлых?

– Да, конечно, – загадочно ответил он.

– Я имею в виду, за Оксфорд или за Кембридж?

– Да, – он покачал головой. – За кого-то из них. Переменных слишком много, и они слишком сложные, чтобы предсказать успех, Ватсап.

– Сомс, я спрашивал, за кого вы болеете, а не просил предсказать победителя.

Он бросил на меня уничтожающий взгляд.

– Ватсап, с какой стати я должен болеть за людей, с которыми даже не знаком?

Когда на Сомса нападает хандра, тому всегда есть причина. Я заметил, что он выкладывает из спичек нечто, напоминающее рыбий скелет, и спросил, в чем дело.

– Я вот смотрю, как распределяются весла на лодках, и мне интересно, почему стало традиционным такое неэффективное их расположение.

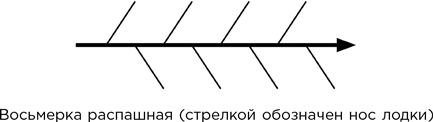
Я перевел взгляд на Темзу, где две лодки как раз занимали места на стартовой линии перед ежегодной Университетской гонкой.

– Традиция часто неэффективна, – поучающе заметил я, – поскольку суть ее заключается в том, чтобы делать все точно так, как делалось всегда, а не задаваться вопросом, как сделать лучше всего. Но я не вижу здесь никакой неэффективности. Восемь гребцов, и весла обращены по очереди то на правую сторону, то на левую. Такая лодка называется распашной, и ее устройство представляется мне симметричным и разумным.

Сомс недовольно хмыкнул.

– Симметричной? Тьфу! Вовсе нет. Все весла одного борта расположены впереди по отношению к веслам другого борта. Разумной? Когда гребцы налегают на весла, асимметрия создает крутящую силу, которая заставляет лодку отклоняться в одну сторону.

– Но именно поэтому, Сомс, на лодке есть рулевой. Который направляет лодку при помощи руля.

– Который порождает сопротивление поступательному движению лодки.

– Ах! Но как еще можно расположить весла? Невозможно ведь посадить двух гребцов рядом, бок о бок.

– Существует 68 вариантов, Ватсап; 34, если считать зеркально симметричные варианты одинаковыми. Кстати говоря, наши немецкие и итальянские друзья пользуются другими схемами расположения весел, – он выложил перед собой из спичек две скелетообразные схемы.

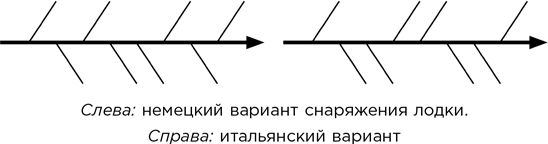
Я в недоумении уставился на них.

– Но ведь такие странные варианты расположения весел наверняка страдают от еще бо́льших проблем!

– Возможно. Давайте посмотрим, – он поджал губы и погрузился в размышления. – В этом деле бесчисленное количество практических вопросов, Ватсап, которые требуют более сложного анализа. Не говоря уже о том, что у меня не хватит спичек. Поэтому я ограничусь простейшей моделью, какую смогу придумать, и буду надеяться, что она подскажет мне что-нибудь полезное. Предупреждаю заранее, что результаты будут не слишком определенными.

– Достаточно справедливо, – сказал я.

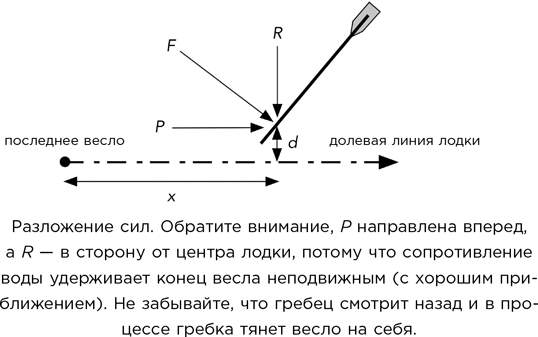
– Теперь рассмотрим одно отдельно взятое весло и рассчитаем силы, действующие на уключину, в которой оно вращается, в ходе той фазы гребка, когда весло находится в воде. Для простоты я буду считать, что все гребцы обладают одинаковой силой и гребут с идеальной синхронностью, так что прикладывают одинаковую силу F в любой заданный момент. Затем я раскладываю эту силу на компоненты P (параллельный оси лодки) и R (направленный к ней под прямым углом).

– Все эти силы изменяются во времени, – заметил я.

Он кивнул.

– Важно здесь то, что специалисты по механике называют моментом каждой силы, – степень, в которой она поворачивает лодку вокруг какой-то выбранной точки. Находят его, как вы помните из истории с палимпсестом Архимеда, перемножением силы на расстояние от точки ее приложения по перпендикуляру до этой точки.

Настала моя очередь кивнуть. Я был уверен, что припоминаю что-то в этом роде.

– Я отмечаю положение ближайшего к корме весла точкой. Это и будет наша выбранная точка. Далее, сила P имеет момент Pd относительно точки, в которой крепление уключины весла пересекается с центральной продольной осью лодки, если это весло расположено на левой стороне. Но если оно располагается справа, момент будет равен – Pd, поскольку сила при этом закручивает лодку в противоположном направлении. Обратите внимание: эти моменты для всех четырех весел на одном борту лодки одинаковы. Следовательно, суммарный момент всех восьми весел равен 4Pd – 4Pd, то есть 0.

– Вращающие силы уравновешивают друг друга!

– Для продольных составляющих P – да, уравновешивают. Однако момент силы R у каждого весла свой, поскольку зависит от расстояния x между этим веслом и крайним кормовым. Если говорить конкретно, этот момент равен Rx. Если расстояние между соседними веслами везде одинаково и равно c, то x принимает значения

0 cR 2cR 3cR 4cR 5cR 6cR 7cR

по мере продвижения от кормы к носу. Поэтому суммарный момент равен

± 0 ± cR ± 2cR ± 3cR ± 4cR ± 5cR ± 6cR ± 7cR,

где ставится знак плюс для весел левого борта и знак минус – для весел правого борта.

– Почему?

– Силы на левой стороне поворачивают лодку по часовой стрелке, Ватсап, а силы по правой стороне – против. Можно упростить это выражение до (± 0 ± 1 ± 2 ± 3 ± 4 ± 5 ± 6 ± 7) cR, где последовательность плюсов и минусов соответствует последовательности сторон, на которые смотрят весла.

– А теперь рассмотрим стандартное расположение весел на спортивной распашной восьмерке. Последовательность знаков здесь такова:

+ – + – + – + –,

так что суммарный крутящий момент равен

(0–1 + 2–3 + 4–5 + 6–7) cR = –4cR.

В первой фазе гребка R направлена внутрь, но, когда весло начинает уходить назад, направление R меняется, она начинает действовать наружу. Поэтому лодка в ходе гребка сначала поворачивается в одном направлении, затем в другом, то есть вихляет на ходу. Рулевой должен при помощи руля корректировать ход лодки, а это, как я уже сказал, порождает сопротивление.

– А что в немецком варианте? Здесь суммарный крутящий момент равен

(0–1 + 2–3 – 4 + 5–6 + 7) cR = 0,

какими бы ни были c и R. Так что лодка в этом варианте не склонна вилять.

– А у итальянцев? – воскликнул я. – О, дайте мне попробовать! Суммарный крутящий момент равен

(0–1–2 + 3 + 4–5–6 + 7) cR = 0.

Тоже! Как замечательно!

– Вот именно, – отозвался Сомс. – А теперь, Ватсап, вопрос для вашего живого ума. Являются ли немецкий и итальянский варианты – или их зеркальные отражения, которые ничем, в сущности, от них не отличаются, – единственными способами обнулить вращающие силы? – должно быть, он заметил выражение моего лица, поскольку добавил: – Вопрос сводится к разделению чисел от 0 до 7 на две группы по четыре, каждая из которых при сложении даст одну и ту же сумму. А именно 14, поскольку все эти числа в сумме дают 28.