– Ну, Сомс, эта забавная небольшая головоломка сможет поднять вам настроение, – я перебросил Daily Reporter другу и компаньону, почти знаменитому детективу, страдавшему в настоящее время от приступа депрессии потому только, что его конкурент из дома напротив явно достиг большей известности и имел все шансы это преимущество сохранить.

Он, издевательски рассмеявшись, отбросил газету в сторону.

– Ватсап, у меня не хватит энергии на чтение.

– Тогда я сам вам прочту, – ответил я. – Кажется, знаменитый математик Артур Кейли опубликовал статью в «Записках Королевского географического общества», в которой задал вопрос…

– Вопрос о том, можно ли раскрасить произвольную карту не более чем четырьмя красками так, чтобы соседние области оказались окрашенными в разные цвета, – прервал меня Сомс. – Это давняя проблема, Ватсап, и я боюсь, что ответ на этот вопрос не будет получен при нашей жизни. – Я ничего не сказал, надеясь вытащить его на дальнейший разговор, поскольку это была самая длинная фраза, которую он произнес почти за неделю. Мой план сработал, и после минуты неловкого молчания он продолжил: – Молодой человек по имени Фрэнсис Гутри сформулировал эту задачу за два года до моего рождения. Будучи не в состоянии решить ее самостоятельно, он обратился к своему брату Фредерику, ученику профессора Огастеса де Моргана.

– Ах да, Гусси, – вставил я, поскольку был знаком с семьей этого достойного восхищения чудака, автора книги «Бюджет парадоксов» и бича всех свихнувшихся на математике.

– Де Морган, – продолжал Сомс, – ничего не добился, поэтому попросил заняться ею великого ирландского математика сэра Уильяма Роуэна Гамильтона, который, однако, ответил ему отказом. На том все и застопорилось до тех пор, пока Кейли вновь не взялся за эту задачу. Хотя я не представляю, почему он решил опубликоваться именно в этом журнале.

– Возможно, потому, – предположил я, – что географы интересуются картами? – но Сомс только презрительно хмыкнул.

– Не в таком аспекте, – раздраженно отмахнулся он. – Географ раскрасит области на карте в соответствии с политической обстановкой, не обращая внимания на соседство. Смотрите, Кения, Уганда и Танганьика расположены рядом, но на всех картах Британской империи все они окрашены в одинаковый розовый цвет.

Я признал справедливость этого утверждения. Нашей дорогой королеве не понравилось бы, если бы их раскрасили иначе.

– Но, Сомс, – я продолжал настаивать, – вопрос от этого не становится менее интересным. Даже более, поскольку никто, похоже, не в состоянии на него ответить.

Сомс что-то проворчал.

– Давайте все же попробуем, – сказал я и быстро нарисовал условную карту.

– Забавно, – заметил Сомс. – А почему вы сделали все области круглыми?

– Потому что любая область без дырок топологически эквивалентна кругу.

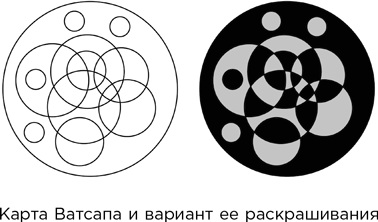
Сомс поджал губы.

– Тем не менее это плохой выбор, Ватсап.

– Почему? Мне кажется…

– Ватсап, вам много что кажется, но мало что на самом деле имеет место быть. Хотя любая отдельная область топологически равноценна кругу, две или большее число областей могут перекрываться способом, невозможным для двух или нескольких кругов. Об этом свидетельствует тот факт, что для вашей карты достаточно всего двух красок, – и он заштриховал примерно половину областей.

– Ну да, но я уверен, что более сложная карта того же рода…

Сомс покачал головой.

– Нет-нет, Ватсап. Любая карта, состоящая исключительно из круглых областей, даже если эти области разных размеров и перекрываются разными, сколь угодно сложными способами, может быть раскрашена в две краски. Считая, как обычно и делается в подобных вопросах, что «соседние» области должны иметь общие участки границы, а не отдельные изолированные общие точки.

У меня отвалилась челюсть.

– Теорема о двух красках! Поразительно! – Сомс соизволил пожать плечами. – Но как такую теорему можно доказать?

Сомс откинулся в кресле.

– Вы знаете мои методы.