Замостить плоскость без промежутков и перекрытий можно множеством различных фигур. Единственными правильными многоугольниками, с помощью которых можно это проделать, являются равносторонний треугольник, квадрат и шестиугольник.

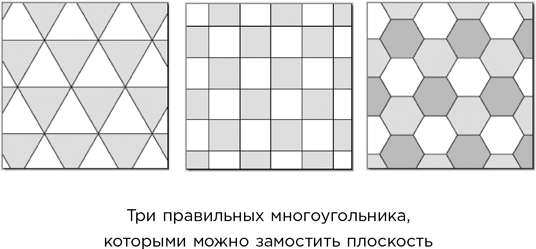
Кроме них плоскость можно замостить громадным количеством менее правильных фигур, таких как семисторонний многоугольник на следующем рисунке. Он получен из правильного семиугольника путем зеркального отображения трех его сторон относительно линии, соединяющей их концы.

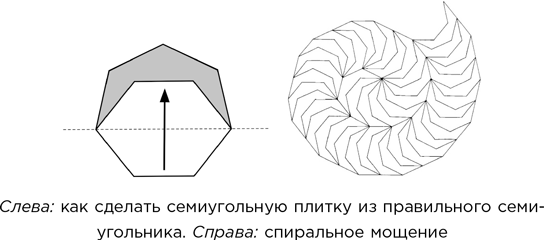
Мощение правильными многоугольниками периодично, то есть его элементы повторяются бесконечно в двух различных направлениях, как узор на обоях. Спиральное мощение не периодично. Однако описанным здесь семиугольником можно замостить плоскость и периодически.

Существуют ли фигуры, которыми можно замостить плоскость, но нельзя сделать это периодически? Вопрос этот глубоко связан с математической логикой. В 1931 г. Курт Гёдель доказал, что в арифметике существуют неразрешимые задачи, то есть утверждения, для которых никакой алгоритм не в состоянии определить, истинны они или ложны. (Алгоритм – это систематический процесс, который гарантированно прекращается при получении верного ответа.) Из этой теоремы следует другая, более драматичная: в арифметике существуют утверждения, которые невозможно ни доказать, ни опровергнуть.

Приведенный Гёделем пример такого утверждения был несколько надуманным, и специалисты по математической логике долго гадали, существуют ли более естественные нерешаемые проблемы. В 1961 г. Хао Ван работал над проблемой домино: если имеется конечное число фигур для мощения, то существует ли алгоритм, который был бы способен определить, можно ли этими фигурами замостить плоскость? Ван показал, что если существует подходящий набор, которыми можно замостить плоскость, но нельзя замостить ее периодически, то такого алгоритма не существует. Его идея состояла в том, чтобы перевести правила логики в формы плиток и использовать результаты вроде гёделевых. И она сработала: в 1966 г. Роберт Бергер нашел набор из 20 426 таких плиток, доказав тем самым, что проблема домино действительно неразрешима.

20 000 различных фигур – это много. Бергеру удалось снизить их число до 104; затем Ганс Лейхли снизил его до 40. Рафаэль Робинсон довел число форм до шести. Роджер Пенроуз, открыв в 1973 г. так называемые плитки Пенроуза (см. «Кабинет…» с. 149), еще уменьшил их число, всего до двух. Получилась интригующая математическая загадка: существует ли единственная фигура, с помощью которой можно замостить плоскость, но нельзя замостить ее периодически? (При этом можно использовать также зеркальное отражение той же фигуры.) Ответ был найден в 2010 г. Джошуа Соколаром и Джоан Тейлор, и ответ этот – «да».

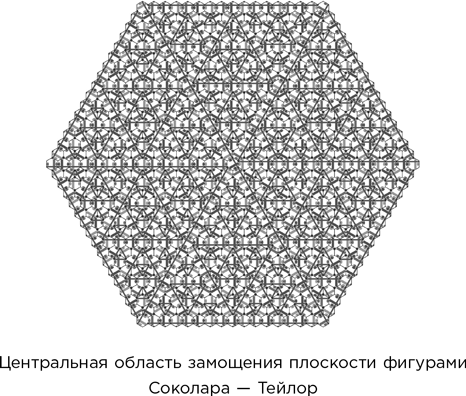
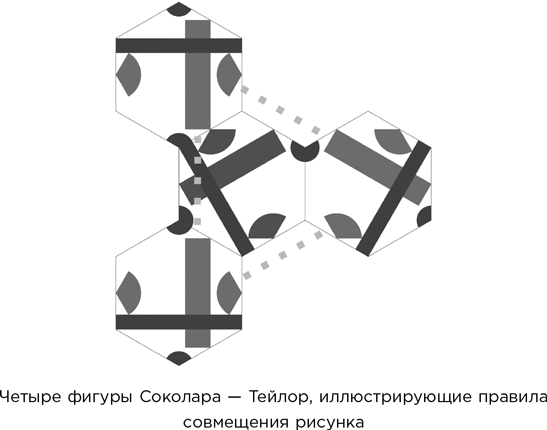
Предложенная ими фигура показана на рисунке. Это «разрисованный шестиугольник» с дополнительными «правилами стыковки», и он отличается от собственного зеркального отражения. Рисунки на плитке должны стыковаться вполне определенным образом – так, как показано на рисунке.

На следующем рисунке показана центральная область замощенной такими фигурами плоскости. Можно заметить, что узор на ней не выглядит периодическим. В статье объясняется, почему такое мощение можно распространить на всю площадь и почему результат не может быть периодическим. Подробности можно узнать непосредственно из статьи.