6. Новые решения старой задачи. Гипотеза Морделла

Настало время нам вновь окунуться в теорию чисел и двинуться по направлению к Великой теореме Ферма. Чтобы подготовить почву, я начну с менее известной, но, по мнению некоторых, еще более важной задачи. В 2002 г. Эндрю Гранвиль и Томас Такер представили ее следующим образом:

Упомянутый здесь Луис Морделл — британский специалист по теории чисел, родившийся в США в еврейской семье литовского происхождения, а Герд Фальтингс — немецкий математик. Вопрос, о котором идет речь, приобрел известность как гипотеза Морделла. В цитате, помимо прочего, обозначен ее точный статус: блестяще доказана Фальтингсом.

Гипотеза Морделла относится к крупному отделу теории чисел — к диофантовым уравнениям. Они названы так в честь Диофанта Александрийского, написавшего где-то около 250 г. н. э. знаменитую книгу «Арифметика». Считается, что первоначально она включала в себя 13 книг, но до нас дошли лишь шесть, и все в позднейших копиях. Это не был арифметический текст в буквальном смысле, т. е. речь в нем не шла о сложении и умножении. По существу, это был первый текст по алгебре, в котором были собраны почти все познания греков о том, как нужно решать уравнения. В нем использовалась даже некая рудиментарная форма алгебраического языка: судя по всему, для обозначения неизвестного в ней использовался вариант ς греческой буквы «сигма» (мы для этого используем x), для квадрата неизвестного (вместо нашего x²) — Δ^Υ, а для куба неизвестного (вместо нашего x³) — Κ^Υ. Сложение обозначалось тем, что символы помещались рядом друг с другом, а вычитание имело собственный символ. Величина, обратная неизвестному (наше 1/x), выглядела как ςχ и т. д. Эти обозначения восстановлены на основании позднейших копий и переводов и могут быть не вполне точными. Классическая греческая математика требовала, чтобы решения уравнений были рациональными числами, т. е. дробями вроде 22/7, сформированными из целых чисел. Часто требовалось даже, чтобы они сами были целыми числами. Все задействованные числа были положительными: представление об отрицательных числах появилось несколькими столетиями позже в Китае и Индии. Сегодня мы называем подобные задачи диофантовыми уравнениями. В «Арифметике» можно обнаружить замечательно глубокие результаты. В частности, Диофант, судя по всему, знал, что любое целое число может быть представлено в виде суммы четырех полных квадратов целых чисел (включая нуль). Лагранж впервые доказал это в 1770 г. Но нас в данном случае интересует другой результат — формула для пифагоровых троек, в которых сумма двух полных квадратов дает третий полный квадрат. Название происходит от теоремы Пифагора: именно таким соотношением связаны стороны прямоугольного треугольника. Самый известный пример — знаменитый треугольник 3, 4, 5: (3² + 4² = 5²). Еще один пример — треугольник 5, 12, 13: (5² + 12² = 13²). Рецепт поиска пифагоровых троек сформулирован в виде двух лемм (вспомогательных утверждений), помещенных перед Предложениями 29 и 30 в Книге X «Начал» Евклида.

Приведенная у Евклида процедура позволяет получить бесконечно много пифагоровых троек. Морделл знал несколько других диофантовых уравнений, для которых существует формула с бесконечным числом решений. Он знал также, что существует другой тип диофантовых уравнений, имеющих бесконечно много решений, которые не описываются формулой. Существуют так называемые эллиптические кривые — достаточно глупое название, поскольку они не имеют практически никакого отношения к эллипсам, — где бесконечность числа решений возникает потому, что любые два решения можно скомбинировать так, чтобы получилось еще одно. Сам Морделл доказал одно из фундаментальных свойств таких уравнений: все бесконечное множество решений может быть получено при помощи этого процесса из конечного их числа.

Помимо этих двух известных типов уравнений, все остальные диофантовы уравнения, которые мог придумать Морделл, попадали в одну из двух категорий. Либо про уравнение было известно, что число его решений конечно (или их просто нет), либо никто не мог сказать наверняка, является ли число его решений конечным или бесконечным. В сущности, ничего нового в этом не было, но Морделлу показалось, что он видит в этом закономерность, которую до него никто не замечал. Закономерность эта относилась вовсе не к теории чисел — скорее, ее можно было отнести к топологии. Чтобы разобраться в этом, необходимо было рассматривать решения уравнений в комплексных числах, а не в рациональных или целых. А это, что ни говори, противоречило самому духу диофантовых уравнений.

Здесь стоит добавить несколько деталей, которые пригодятся нам позже. Не бойтесь формул: они нужны мне в основном для того, чтобы можно было ссылаться на что-то конкретное. Сосредоточьтесь на рассказе, который лежит за ними.

Разделив обе части уравнения на z², получим

Согласно главе 3, это означает, что пара рациональных чисел (x/z, y/z) лежит на единичной окружности в плоскости. Далее пифагорово уравнение берет начало в геометрии и имеет геометрическую интерпретацию: связанный с ним треугольник является прямоугольным. Формула, которую я только что вывел, позволяет дать чуть другую геометрическую интерпретацию, причем не одной, а всех пифагоровых троек. Решения пифагорова уравнения непосредственно соответствуют всем рациональным точкам единичной окружности. Мы считаем точку рациональной, если рациональны обе ее координаты.

Из этого можно сделать немало интересных выводов. Если привлечь тригонометрию (но можно обойтись и одной алгеброй), обнаружится, что для любого числа t точка

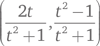
лежит на единичной окружности. Более того, если t рационально, то рациональна и эта точка. Все рациональные точки возникают подобным образом, так что мы получили исчерпывающую формулу для всех решений пифагорова уравнения. Она эквивалентна евклидовой формуле, которая, в свою очередь, совпадает с диофантовой. К примеру, если t = 22/7, формула даст результат

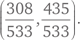
Можно проверить: 308² + 435² = 533². Для нас точная формула не слишком важна, важно, что она существует.

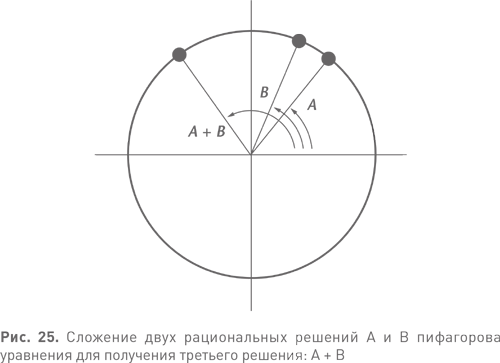
Это не единственное диофантово уравнение, для всех решений которого существует единая формула, но таких уравнений относительно немного. Например уравнения Пелля, такие как x² = 2y² + 1. У этого уравнения бесконечно много решений (3² = 2 × 2² + 1, 17² = 2 × 12² + 1) и для них существует общая формула. Однако упорядоченность пифагоровых троек этим не ограничивается; геометрия подсказывает нам и другие закономерности. Предположим, мы имеем две пифагоровы тройки. Следственно, существует два соответствующих им решения пифагорова уравнения — две рациональные точки на окружности. Геометрия предлагает естественный способ «сложить» эти точки. Начнем с точки (1, 0), в которой окружность пересекает горизонтальную ось, и найдем углы между этой точкой и двумя точками-решениями. Сложим эти два угла (см. рис. 25) и посмотрим, что получится. Точка, разумеется, тоже лежит на окружности, и короткий расчет покажет, что она также рациональна. Таким образом, имея два любых решения, мы можем получить третье. Математики уже заметили множество подобных фактов, причем большинство из них обретает смысл сразу же, как только мы вспоминаем о рациональных точках на окружности.

«Короткий расчет», который я небрежно пропустил, делается с использованием тригонометрии. Классические тригонометрические функции, такие как синус и косинус, теснейшим образом связаны с геометрией окружности. В расчете, на который я ссылался, используются стандартные, довольно элегантные формулы вычисления синуса и косинуса суммы двух углов через синусы и косинусы самих углов. Существует много способов получения синусов и косинусов, и один из них, достаточно изящный, основан на интегральном исчислении. Если вы будете интегрировать алгебраическую функцию 1/√1-x², то результат может быть выражен, используя функцию синус. Точнее, нам нужна функция, обратная синусу: угол, синус которого равен интересующему нас числу.

Интеграл возникает, когда мы пытаемся вывести формулу длины дуги окружности методами математического анализа, а геометрия окружности дает простое, но очень важное следствие для этого результата. Длина единичной окружности равна 2π, поэтому пройдя расстояние 2π вдоль окружности, вы окажетесь в точности на том же месте. То же можно сказать о любом расстоянии, кратном 2π: по стандартному математическому соглашению положительные целые числа соответствуют направлению против часовой стрелки, а отрицательные — по часовой стрелке. Следовательно, синус и косинус числа остаются неизменными при добавлении к аргументу величины 2π, взятой целое число раз. Мы говорим, что эти функции периодические с периодом 2π.

Аналитики XVIII и XIX вв. обобщили эту интегральную формулу и нашли целую группу интересных новых функций, аналогичных знакомым тригонометрическим. Эти новые функции выглядели загадочно; они были периодическими, как синус и косинус, но хитроумно периодическими. Вместо одного периода, к примеру 2π (или кратных ему), они имели два независимых периода. Если вы попытаетесь проделать такое с действительными функциями, то получите всего лишь константы, но для комплексных чисел здесь открываются широкие возможности.

Начало исследованиям в этой области положили итальянский математик Джулио ди Фаньяно и плодовитый Эйлер. Фаньяно пытался при помощи интегрального исчисления найти длину дуги эллипса, но не сумел вывести формулу в явном виде. Сегодня это уже не удивительно, ведь мы знаем, что такой формулы не существует. Однако он заметил, что длины различных особых дуг эллипса находятся между собой в определенных отношениях. Результаты своих исследований Фаньяно опубликовал в 1750 г. Эйлер в аналогичной ситуации заметил те же отношения и представил их в виде формального отношения интегралов. Они похожи на интеграл, связанный с функцией синуса, но квадратичное выражение под знаком квадратного корня сменяется кубическим многочленом или многочленом четвертой степени, к примеру, таким: (1 − x²) (1 − 4x²).

В 1811 г. Адриен Мари Лежандр опубликовал первую книгу объемного трехтомного трактата об этих интегралах, известных как эллиптические благодаря своей связи с длиной дуги сегмента эллипса. Однако он умудрился пройти мимо самого важного их свойства: существования новых функций, аналогичных синусу и косинусу, обратные функции к которым достаточно просто выражают величину интеграла. Гаусс, Нильс Хенрик Абель и Карл Якоби быстро заметили упущение. Гаусс оставил свои мысли при себе, что для него вполне типично. Абель в 1826 г. представил во Французскую академию собственную работу, но Коши, президент Академии, потерял рукопись, и опубликована она была только в 1841 г., через 12 лет после трагической ранней кончины Абеля от чахотки. Однако в 1827 г. вышла другая статья Абеля на ту же тему. Якоби положил новые «эллиптические функции» в основу громадного тома, опубликованного в 1829 г., и этот труд направил исследования в области комплексного анализа по совершенно новому пути.

В результате был выявлен целый комплекс взаимосвязанных свойств, аналогичных свойствам тригонометрических функций. Оказалось, что соотношение, замеченное Фаньяно и Эйлером, можно интерпретировать иначе, в виде простого списка формул, связывающих эллиптические функции суммы двух чисел с эллиптическими функциями самих чисел. Но самая интересная черта эллиптических функций оставляет тригонометрические функции далеко позади. Эллиптические функции не просто периодические; для них характерна двойная периодичность. Линия одномерна, поэтому и рисунок ее может повторяться только в одном направлении, вдоль линии. Комплексная плоскость двумерна, так что рисунок на ней может повторяться, как на обоях: вдоль бумажной полосы и одновременно поперек — вдоль стены, на соседние полосы. С каждой эллиптической функцией связаны два независимых комплексных числа (ее периоды), прибавление любого из которых к переменной не меняет значение функции.

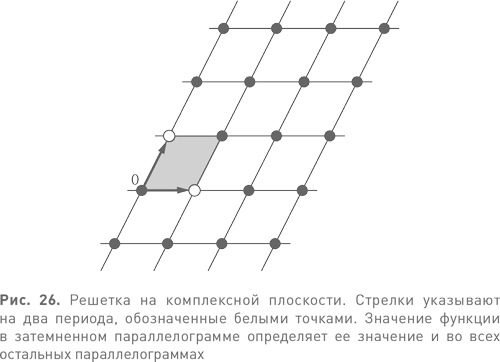
Повторяя этот процесс, мы приходим к выводу, что значение функции не меняется при добавлении к переменной любой целочисленной комбинации двух периодов. Эти комбинации можно интерпретировать и геометрически: они определяют на комплексной плоскости решетку, которая разбивает плоскость на параллелограммы; все, что происходит в одном параллелограмме, повторяется и во всех остальных (см. рис. 26). Если мы рассмотрим отдельно взятый параллелограмм и то, как он соединяется с соседними, то получим, что нам придется отождествить противоположные его стороны, как тор определяется через отождествление противоположных сторон квадрата (см. рис. 12). Параллелограмм, противоположные стороны которого попарно отождествляются, топологически тоже представляет собой тор. Иными словами, точно так же, как синус и косинус связаны с окружностью, эллиптические функции связаны с тором.

Есть здесь и связь с теорией чисел. Я сказал, что функция, обратная синусу, получается путем интегрирования формулы, в которой фигурирует квадратный корень из квадратного трехчлена (т. е. многочлена второй степени). Эллиптические функции в этом похожи, но квадратный трехчлен в них заменяется на многочлен третьей или четвертой степени. Случай с четвертой степенью уже упоминался, потому что исторически он появился первым, но теперь давайте сосредоточимся на случае с многочленом третьей степени. Если мы обозначим квадратный корень как y, а многочлен как ax³ + bx² + cx + d, где a, b, c и d — числовые коэффициенты, то x и y удовлетворяют уравнению:

Это уравнение можно рассматривать в нескольких различных контекстах, в зависимости от того, какие ограничения наложены на переменные и коэффициенты. Если все это действительные числа, уравнение определяет кривую на плоскости. Если это комплексные числа, то специалисты по алгебраической геометрии все равно называют множество решений этого уравнения кривой просто по аналогии. Но теперь это кривая в пространстве пар комплексных чисел, четырехмерном в действительных координатах. И кривая в данном случае — это поверхность с точки зрения действительных координат.

На рис. 27 показаны типичные действительные эллиптические кривые y² = 4x³ − 3x + 2 и y² = 4x³ − 3x. Поскольку y появляется в уравнении в виде квадрата, кривая симметрична относительно горизонтальной оси. В зависимости от коэффициентов это либо одна волнообразная кривая, либо кривая с отдельным овальным компонентом. В комплексных числах кривая всегда представляет собой единое связное множество.

Если мы потребуем, чтобы переменные и коэффициенты были рациональными, в игру вступит теория чисел и мы получим диофантово уравнение. Его графическое представление зачем-то называется эллиптической кривой, хотя совершенно не похоже на эллипс. Все дело в том, что это уравнение связано с эллиптическими функциями. Это как назвать окружность треугольной кривой только потому, что она связана с тригонометрией. Однако это название уже высечено на скрижалях, так что нам придется мириться с ним.

Теория эллиптических функций — глубокая и богатая теория, математики открыли у эллиптических кривых бессчетное количество красивых свойств. Одно из них аналогично тому, как мы объединяем два решения пифагорова уравнения, складывая соответствующие углы и получая третье решение. Две точки на эллиптической кривой можно «сложить», проведя через них прямую линию и посмотрев, в какой точке она пересечет кривую в третий раз (см. рис. 28). (Заметим, что третья точка обязательно существует, поскольку уравнение кубическое. Однако она может оказаться «в бесконечности» или совпасть с одной из первых двух точек, если прямая пройдет по касательной к кривой.) Если первые две точки у нас обозначены как P и Q, обозначим третью как P*Q.

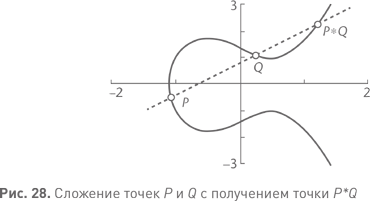
Расчет показывает, что если P и Q — рациональные точки, то и точка P*Q рациональна. Операция * придает набору рациональных точек алгебраическую структуру, но оказывается полезной и при рассмотрении еще одной связанной с этим операции. Выберем любую рациональную точку O на кривой и определим:

Эта новая операция подчиняется некоторым фундаментальным законам обычной алгебры, причем O ведет себя как нуль и превращает множество всех рациональных точек в то, что специалисты по алгебре называют группой (см. главу 10). Важно, что здесь, как с пифагоровыми тройками, можно «сложить» любые два решения и получить третье. То, что «групповой закон» действует на рациональные точки, поразительно: в частности, это означает, что стоит нам найти два рациональных решения диофантова уравнения, и мы автоматически получим множество других решений.

Около 1908 г. Пуанкаре задался вопросом: существует ли конечный набор решений, такой, чтобы из него можно было получить все остальные решения последовательным применением групповой операции? Это важно, потому что из существования такого набора следует, что все рациональные решения можно охарактеризовать при помощи конечного списка решений. В интереснейшей работе 1922 г. Морделл доказал, что ответ на вопрос Пуанкаре положителен. После этого эллиптические кривые стали центральным элементом теории чисел, поскольку далеко не все диофантовы уравнения могут похвастать такой степенью контроля. Итак, эллиптические кривые, как и пифагорово уравнение, имеют бесконечное множество рациональных решений. Многие диофантовы уравнения, напротив, имеют конечное число или вообще не имеют решений. Я собираюсь немного отклониться от темы и поговорить о целом семействе подобных уравнений и полученном недавно замечательном доказательстве того, что существуют лишь очевидные решения.

Пифагорейцы были увлечены своим уравнением, потому что верили: в основе Вселенной лежат числа. В поддержку этой философии они обнаружили, что музыкальной гармонией управляют простые числовые отношения. Это было установлено экспериментально при помощи наблюдений за звучанием натянутой струны. Струна с такой же степенью натяжения, но вдвое меньшей длины, дает ноту на октаву выше. Это самое гармоничное сочетание двух нот — настолько гармоничное, что звучит даже несколько простовато. В западной музыке следующая по значению гармония — кварта, где одна струна по длине составляет 3/4 другой струны, и квинта, где длина одной струны составляет 2/3 от длины другой.

Начав с 1 и умножая последовательно на 2 или 3, можно получить числа 2, 3, 4, 6, 8, 9, 12 и т. д. — числа вида 2^a3^b. Благодаря связи с музыкой они получили название гармонических. В XIII в. во Франции еврейский ученый по имени Гершон бен Соломон Каталан написал книгу «Врата небес», посвятив три ее части физике, астрономии и метафизике. В 1343 г. епископ Мо убедил его сына (по крайней мере историки считают, что, вероятно, это был его сын) Леви бен Гершома написать математическую книгу «Гармония чисел». В нее вошла, в частности, задача, которую впервые поставил композитор и теоретик музыки Филипп де Витри: когда два гармонических числа могут различаться на единицу? Подобные пары найти несложно: сам де Витри знал их четыре: (1, 2), (2, 3), (3, 4) и (8, 9). Но Гершом доказал, что это все возможные решения и других не существует.

Среди перечисленных де Витри пар гармонических чисел наибольший интерес привлекает пара (8, 9). Первое число в ней — куб, 2³; второе — квадрат, 3². Математики заинтересовались, могут ли другие квадраты и кубы различаться на единицу; Эйлер доказал, что не могут, за исключением тривиального случая (0, 1) и случая (−1, 0), если разрешены отрицательные числа. В 1844 г. уже другой Каталан опубликовал более всеобъемлющее заявление, о котором, должно быть, думали многие математики, но которое никто до него не счел нужным озвучить. Речь идет о бельгийском математике Эжене Шарле Каталане, который в 1844 г. написал в один из ведущих математических журналов того времени Journal für die Riene und Angewandte Mathematik следующее:

Это утверждение получило известность как гипотеза Каталана. Показатели степени m и n здесь — целые числа больше 1.

Несмотря на частичные успехи, гипотеза Каталана долгое время упорно противостояла всем усилиям математиков, пока в 2002 г. ее не доказал вдруг Преда Михайлеску. Этот математик родился в 1955 г. в Румынии, а в 1973 г. поселился в Швейцарии и к тому времени только что получил докторскую степень. Темой его диссертации было «Деление кругов и проверка на простоту», и речь в ней шла о применении теории чисел при проверке на простоту (глава 2). Эта задача не имеет особого отношения к гипотезе Каталана, но Михайлеску пришло в голову, что методы-то его точно имеют к ней отношение. В них он отталкивался от идей, уже упоминавшихся мной в главе 3: гауссового построения правильного 17-угольника и связанных с этим алгебраических уравнений, решения которых называют круговыми числами. Доказательство получилось достаточно сложным и произвело в математическом сообществе настоящий фурор. Из него явствует, что какие бы величины мы ни выбрали для двух показателей степени, число решений остается конечным — и помимо очевидных решений с участием 0 и ±1 единственное решение, представляющее интерес, это 3² − 2³ = 1.

Приведенные примеры наглядно показывают, что одни диофантовы уравнения имеют бесконечное множество решений, а другие — нет. Что тут интересного, скажете вы, эти два варианта перекрывают весь спектр возможностей. Но если вы спросите, какие уравнения к какому типу относятся, все станет намного интереснее.

Морделл готовил учебник по диофантовым уравнениям. В то время эта область математики напоминала биологию на раннем этапе ее развития: множество собранных коллекционерами бабочек, и никакой систематической классификации. Наука пребывала почти в том же состоянии, в каком ее оставил Диофант, только беспорядка стало еще больше: это был бессистемный набор ловких трюков, для каждого типа уравнений свой, и вот такой не слишком подходящий для учебника материал отчаянно нуждался в систематизации, чем Морделл и занялся.

В какой-то момент он, должно быть, заметил, что все уравнения, достоверно имеющие бесконечное множество рациональных решений, — такие как пифагорово уравнение или эллиптические кривые — имеют одну общую черту. Он сосредоточился на одном классе уравнений — на тех, в которых (после перевода в рациональную форму, как я сделал с пифагоровым уравнением) присутствует всего две переменных. Есть два случая, когда нам заранее известно, как найти бесконечное множество решений. Пример одного из них — пифагорово уравнение в эквивалентной форме x² + y² = 1. В этом случае существует формула для нахождения решений. Вставьте в эту формулу любое рациональное число и получите рациональное решение, причем формула позволяет получить все решения. Пример второго случая — эллиптические кривые: здесь существует процесс, позволяющий получать новые решения из старых, и гарантия того, что если начать с подходящего конечного набора решений, этот процесс позволит получить их все.

Гипотеза Морделла утверждает, что во всех случаях, когда уравнение имеет бесконечное множество рациональных решений, должно присутствовать одно из названных свойств. Существует либо общая формула, либо процесс, позволяющий получить все решения из подходящего конечного их набора. Во всех остальных случаях число рациональных решений конечно; примером могут служить уравнения вида x^m — yⁿ = 1, которые фигурируют в гипотезе Каталана. Решения здесь в каком-то смысле случайны и не имеют никакой структурной основы.

Морделл пришел к этому наблюдению немного иным путем. Он обратил внимание на то, что все уравнения с бесконечным числом рациональных решений имеют одно поразительное топологическое свойство. У всех у них род равен 0 или 1. Вспомните из главы 4, что род — это понятие из области топологии кривых, которое указывает на то, сколько в данной поверхности отверстий. Род сферы равен 0, род тора — 1, род тора с двумя отверстиями равен 2 и т. д. Но откуда берутся поверхности в задаче из теории чисел? Из координатной геометрии. Мы видели, что пифагорово уравнение, которое интерпретировано в терминах рациональных чисел и допускает действительные решения, определяет окружность. Морделл сделал еще один шаг и допустил комплексные решения. Любое уравнение с двумя комплексными переменными определяет то, что специалисты по алгебраической геометрии называют комплексной кривой. Однако с точки зрения действительных чисел и зрительного восприятия человека каждое комплексное число двумерно: у него на деле две компоненты — действительная и мнимая части. Так что «кривая» в комплексном смысле есть поверхность для нас с вами. И, как у всякой поверхности, у нее есть род, — вот и все.

Всякий раз, когда про уравнение было известно, что оно имеет конечное число решений, его род равнялся по крайней мере двум. Род важных уравнений, статус которых относительно числа решений не был известен, тоже равнялся по крайней мере двум. Морделл на основании достаточно хлипких, как тогда казалось, указаний сделал отчаянно смелый шаг: он предположил, что любое диофантово уравнение с родом 2 или больше имеет конечное число рациональных решений. Так, по мановению его руки, диофантовы бабочки аккуратно распределились по родственным семействам; точнее говоря, по родам (даже термин подходящий).

В гипотезе Морделла была всего лишь одна крохотная загвоздка. Она связала между собой две чрезвычайно разные вещи: рациональные решения и топологию. В то время подобная связь казалась в высшей степени неубедительной. Если даже она существовала, то никто не знал, как ее искать; непонятно было даже, как подступиться к этой проблеме. Так что гипотеза представляла собой отчаянное, ничем не подтвержденное заявление, обещавшее, однако, громадные потенциальные дивиденды.

В 1983 г. Фальтингс опубликовал эффектное доказательство того, что фантастическое предположение Морделла на самом деле верно. Его доказательство было построено на методах алгебраической геометрии. Совершенно другое доказательство, основанное на аппроксимации действительных чисел рациональными, вскоре нашел Пауль Войта, а в 1990 г. Энрико Бомбиери опубликовал упрощенное доказательство, основанное примерно на тех же принципах. Существует приложение теоремы Фальтингса к Великой теореме Ферма — проблеме, о которой мы будем подробно говорить в главе 7. Оно утверждает, что для любого целого n, большего или равного 3, уравнение xⁿ + yⁿ = 1 имеет конечное число целых решений. Род соответствующей кривой равен (n − 1) (n − 2)/2, а это по крайней мере 3, если n ≥ 4. Теорема Фальтингса прямо подразумевает, что при любом n ≥ 4 уравнение Ферма имеет в лучшем случае конечное число рациональных решений. Ферма утверждал, что оно вовсе не имеет решений, за исключением случаев, когда x или y равны нулю, так что это было очень серьезное продвижение. В следующей главе мы вернемся к истории Великой теоремы Ферма и посмотрим, как заявление ученого подтвердилось.