5. Сферическая симметрия. Гипотеза Кеплера

Все началось со снежинки.

Снег обладает странной красотой. Он падает с небес пушистыми белыми хлопьями; он летит по ветру и образует мягкие холмы и гребни, покрывающие все вокруг; он сам по себе обретает неземные странные формы. Он холодный. По нему можно кататься на лыжах, на санках, можно лепить из него снежки и снеговиков… А если не повезет, можно оказаться погребенным под тысячетонной снежной лавиной. Исчезая, он не возвращается на небо — по крайней мере непосредственно в виде белых хлопьев. Он превращается в обычную воду, которая, конечно, может испариться и вернуться на небо, но может и течь ручьями и реками вниз, к морю, а потом долго-долго обитать в океане. Снег — форма льда, а лед — это замороженная вода.

Все сказанное не ново. Вероятно, это знали еще неандертальцы.

Снежинки ни в коем случае нельзя назвать бесформенными комками. В первозданном виде (до того, как начинается процесс таяния) многие из них представляют собой крохотные затейливые звездочки — плоские, шестигранные и симметричные. Есть и просто шестиугольники. Некоторые снежинки не настолько симметричны, некоторые отличаются заметной толщиной (т. е. имеют третье измерение), но снежинки с шестилучевой симметрией очень типичны и встречаются часто. Снежинки — кристаллы льда. Это тоже не новость, ведь невозможно, увидев кристалл, не узнать его. Но снежинки — не обычные кристаллы с плоскими гранями в виде многоугольников. Самое загадочное свойство снежинок добавляет в картину легкий штрих хаоса: несмотря на одинаковую симметрию, точная структура каждой снежинки уникальна. Говорят, не существует двух одинаковых снежинок. Я часто недоумевал: откуда они могут это знать? Но если достаточно педантично разобраться в том, что считать одинаковым, то выяснится, что цифры говорят в пользу такой позиции.

Почему для снежинок характерна шестилучевая симметрия? Этим вопросом 400 лет назад задался один из великих математиков и астрономов XVII в. — и после некоторых размышлений нашел на него ответ. Поразительно верный ответ, тем более что ученый при этом не проводил никаких особых экспериментов. Он просто свел воедино несколько простых общеизвестных мыслей. К примеру, о том, как располагаются зернышки в гранате.

Этого человека звали Иоганн Кеплер, и у него был очень хороший повод задуматься о снежинках. Жизнь и работа ученого в те времена часто зависели от богатого покровителя, и для Кеплера таковым был Иоганн Вакер фон Вакенфельс. В то время Кеплер служил придворным математиком императора Священной Римской империи Рудольфа II, а Вакер, дипломат, был советником императора. Кеплер хотел сделать своему покровителю новогодний подарок. В идеале он должен был быть недорогим, необычным и занимательным — и приоткрыть перед Вакером дверь в мир замечательных открытий, которые стали возможны благодаря его деньгам. Так что Кеплер собрал свои мысли о снежинках в небольшую книгу, которая и должна была стать подарком. Называлась она «О шестиугольных снежинках» (De Nive Sexangula). Шел 1611 г. В этой книге содержалось короткое замечание (один из основных шагов в рассуждениях Кеплера), и сформулированную в нем математическую загадку никому не удавалось решить на протяжении 387 лет.

Кеплер имел огромный опыт поиска закономерностей. Его важнейшая научная работа — открытие трех фундаментальных законов движения планет. Первый и самый известный из них гласит, что орбиты планет представляют собой эллипсы. Кроме того, Кеплер был мистиком и приверженцем учения пифагорейцев о том, что Вселенная основана на числах, закономерностях и математических формах. Помимо астрономии, он занимался астрологией: математики в те времена нередко выдавали себя за астрологов, поскольку обладали необходимой квалификацией и могли рассчитать, когда асцендент находится в Водолее. Богатые покровители и короли заказывали им составление гороскопов.

В своей книге Кеплер указал, что снег возникает из водяного пара, который сам по себе не имеет формы, но каким-то образом превращается в твердые снежинки с шестилучевой симметрией. Для такого перехода должна быть какая-то причина, считал Кеплер:

«Позволительно спросить, каково это действующее начало, как оно действует, является ли форма искони присущей телу или приобретается под влиянием внешних воздействий, принимает ли материал шестиугольную форму в силу необходимости или по своей природе и что следует считать врожденным: воплощенный в шестиугольном архетип красоты или знание цели, к которой приводит эта форма?»

В поисках ответа на этот вопрос Кеплер рассматривает другие примеры шестиугольных форм в природе. В первую очередь на ум приходят пчелиные соты. Они формируются из двух слоев шестиугольных ячеек, составленных «впритык», так что общие их концы образуют три ромба, т. е. параллелограммы, у которых все четыре стороны одинаковы. Такая форма напомнила Кеплеру о теле, известном как ромбический додекаэдр (см. рис. 15). Это тело не входит в перечень пяти правильных тел, известных пифагорейцам (их систематизировал Евклид), но обладает интересным отличительным свойством: одинаковыми ромбическими додекаэдрами можно полностью, без зазоров заполнить пространство. Эта же форма возникает внутри граната, где маленькие округлые зернышки растут в тесноте и потому вынуждены «изобретать» эффективную упаковку.

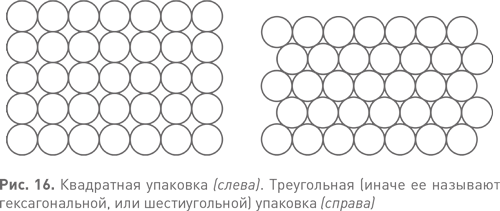
Как всякий разумный математик, Кеплер начинает с простейшего случая, при котором сферы (шарики) образуют единственный плоский слой. По существу, это то же самое, что упаковывать одинаковые кружочки на плоскости. Он находит всего две правильные конфигурации. В одной круги укладываются в квадраты (см. рис. 16 слева); в другой — в равносторонние треугольники (см. рис. 16 справа). Эти конфигурации, повторяемые на бесконечной плоскости, образуют квадратную решетку и треугольную решетку. Слово «решетка» говорит об их пространственной периодичности, повторяющейся в двух независимых направлениях. На рисунке по объективным причинам показаны лишь конечные участки решетки, поэтому на края не нужно обращать внимания. То же можно сказать про размещенные ниже рис. 17–20. На рис. 16 слева и справа показано по пять рядов кругов, и в каждом ряду они соприкасаются с соседями. Однако треугольная решетка немного сплюснута, и ее ряды располагаются ближе друг к другу. Так что круги в треугольной решетке упакованы плотнее, чем в квадратной.

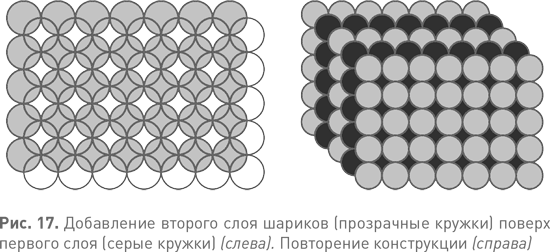
Далее Кеплер задается вопросом, как такие слои можно уложить один на другой, и рассматривает четыре случая. В первых двух все слои уложены по квадратной решетке. При укладывании в стопку шарики каждого ряда можно поместить точно над шариками нижнего ряда. Тогда у каждого шарика будет по шесть непосредственных соседей: четыре в своем слое, один сверху и один снизу. Такая упаковка похожа на трехмерную шахматную доску, сделанную из кубиков; в нее она, кстати, и превратится, если надуть шарики так, чтобы дальше расширяться им было уже некуда. Но это, говорит Кеплер, «не самая плотная упаковка». Ее можно сделать еще плотнее, если сдвинуть верхний слой по диагонали так, чтобы его шарики точно легли во впадины между шариками нижнего слоя (см. рис. 17 слева). Повторим этот процесс для всех слоев (см. рис. 17 справа). Теперь у каждого шарика по 12 соседей: четыре в своем слое, четыре вверху и четыре внизу. Если их надуть, пространство заполнится ромбическими додекаэдрами.

В двух других случаях слои складываются по гексагональной решетке. Если при складывании в стопку поставить шарик над шариком, у каждого шарика будет по восемь соседей: шесть в своем слое, один вверху и один внизу. Опять же шарики верхнего слоя можно поставить над промежутками в нижнем. Тогда у каждого из них будет по 12 соседей: шесть в собственном слое, три вверху и три внизу. Количество соседей такое же, как во втором варианте упаковки квадратных слоев, и Кеплер, проведя тщательный геометрический анализ, показывает, что в реальности этот вариант упаковки полностью совпадает со вторым. Единственная разница заключается в том, что квадратные слои лежат не горизонтально, а под углом. Кеплер пишет: «Таким образом, самая плотная трехмерная упаковка с треугольной решеткой не может существовать без квадратной решетки, и наоборот». К этому я еще вернусь: это важно.

Разобравшись с базовой геометрией упаковки шариков, Кеплер возвращается к снежинке с ее шестилучевой симметрией. Шестигранник напоминает ему о треугольной решетке упаковки шариков на плоскости, в которой каждый шарик соседствует с шестью другими, образуя идеальный шестиугольник. В этом, делает вывод Кеплер, должно быть, и заключается причина шестиконечности снежинок.

Эта глава посвящена, строго говоря, не снежинкам, но данное Кеплером объяснение их симметричности очень похоже на то, что предложили бы сегодня мы, так что стыдно было бы остановиться на этом. Почему они такие разные, но при этом все симметричны? Когда вода кристаллизуется, образуя лед, атомы водорода и кислорода, из которых состоят молекулы воды, укладываются в симметричную структуру — кристаллическую решетку. Эта решетка сложнее любой кеплеровой конструкции из шариков, но строится тоже на основе шестилучевой симметрии. Снежинка растет от крохотного «зернышка» всего из нескольких атомов, организованных в виде маленького кусочка решетки. Это зернышко тоже обладает шестилучевой симметрией; именно оно подготавливает сцену для роста ледяного кристалла в грозовой туче, где ветер бросает миллионы этих кристаллов из стороны в сторону.

Великое разнообразие узоров в снежинках — следствие меняющихся внешних условий. В зависимости от температуры и влажности рост кристалла может идти равномерно по всей границе, и тогда атомы с любой стороны добавляются с одной и той же частотой, и получаются простые шестиугольники. Но рост может идти с разной скоростью в разных местах, и тогда получается древовидная структура. Растущая снежинка путешествует по грозовой туче то вверх, то вниз, и условия вокруг постоянно меняются, причем случайным образом. Но сама снежинка настолько мала, что условия во всех шести ее углах в любой момент времени практически одинаковы. Поэтому все шесть лучей делают одно и то же. Каждая снежинка несет на себе отпечаток своей истории. На практике шестилучевая симметрия никогда не бывает строгой, но часто очень близка к идеалу. Лед — загадочное вещество, поэтому возможны и другие формы — пики, плоские круги, шестигранные призмы, призмы с плоскими концами. Полное описание происходящего вышло бы очень сложным, но определяющим фактором является то, как располагаются атомы в кристаллах льда. Во времена Кеплера атомная теория сводилась в лучшем случае к неопределенным предположениям древних греков. Поразительно, как далеко он сумел зайти в своих выводах, опираясь только на народные наблюдения, мысленные эксперименты и собственную интуицию.

Гипотеза Кеплера не имеет отношения к снежинкам как таковым. Все дело в небрежном замечании о том, что укладка слоев из плотно упакованных шариков, при которой шарики верхнего слоя ложатся во впадины между шариками нижнего, дает «самую плотную возможную упаковку в трех измерениях». Неформально эту гипотезу можно сформулировать так: если вы хотите упаковать много апельсинов в большой ящик, заполнив его при этом как можно плотнее, то укладывать плоды нужно так, как это делает любой торговец фруктами.

Трудность здесь не в том, чтобы найти ответ. Кеплер нам все рассказал. Трудность в том, чтобы доказать, что он был прав. За прошедшие столетия ученые собрали немало косвенных тому свидетельств. Никто не смог предложить более плотную упаковку. Именно такое расположение атомов часто встречается в кристаллах, где, как считается, плотность оптимальна для минимизации затрат энергии — это стандартный принцип, по которому созданы многие природные формы. Этого оказалось достаточно, чтобы убедить большинство физиков. И никто не смог доказать, что ничего лучшего не существует. В более простых вопросах такого рода, вроде упаковки кругов на плоскости, обнаружились скрытые глубины. Надо сказать, весь этот раздел математики сложен и полон неожиданностей. Все это тревожило математиков, хотя большинство из них тоже считали, что Кеплер дал верный ответ. В 1958 г. Амброз Роджерс описал гипотезу Кеплера как то, «во что многие математики верят, а все физики знают и так». В этой главе рассказывается, как математики обратили веру в точное знание.

Чтобы понять, что именно они сделали, нам придется как следует приглядеться к кеплеровой конструкции из шариков, известной как гранецентрированная кубическая решетка. Стоит сделать это, и начинают проявляться тонкости стоявшей перед математиками задачи. Первым на ум приходит вопрос: почему мы используем слои с квадратной решеткой? В конце концов, самой плотной упаковкой на плоскости (т. е. для одного слоя) является треугольная решетка. Дело в том, что гранецентрированную кубическую решетку можно получить и из слоев с треугольной укладкой шариков; именно в этом суть замечания Кеплера о том, что «треугольная схема укладки не может существовать без квадратной». Однако гранецентрированную кубическую решетку, сложенную из квадратных слоев, проще описывать. Кроме того, так мы убедимся, что гипотеза Кеплера не столь прямолинейна, как укладка апельсинов в ящики.

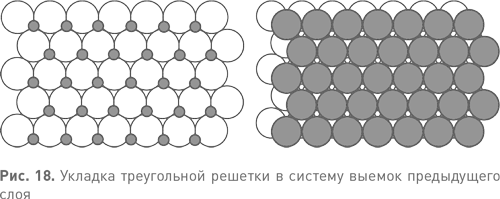
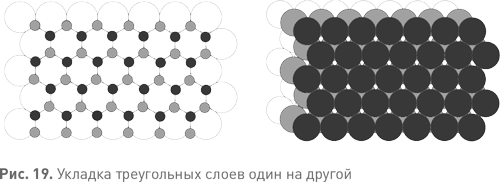
Предположим, что мы начинаем с плоского слоя шариков, уложенных треугольниками (см. рис. 16 справа). Между шариками имеются скругленные треугольные выемки, в которые могут лечь шарики следующего слоя. Когда мы начинали с квадратного слоя, мы могли использовать все выемки без исключения, и положение второго и последующих слоев определялось однозначно. С треугольными слоями не так. Мы не можем использовать все выемки, поскольку они располагаются слишком близко друг к другу. Мы можем использовать только половину. Один из вариантов укладки показан на рис. 18 слева при помощи небольших серых точек для наглядности, а рис. 18 справа демонстрирует, как следует расположить следующий слой шариков. Другой способ уложить новый слой в выемки предыдущего показан на рис. 19 слева темными точками. Эти точки совпадают с выемками второго слоя, так что мы добавляем третий слой в соответствующем положении. Результат показан на рис. 19 справа.

Если мы работаем всего лишь с двумя слоями, разница между двумя вариантами не играет никакой роли. Мы можем без труда получить первый вариант укладки, просто повернув второй вариант на 60°. Эти варианты одинаковы «с точностью до симметрии». Но после укладки первых двух слоев у нас появляются два по-настоящему разных варианта для третьего слоя. Каждый новый слой имеет две системы выемок, показанных на рис. 19 слева светлыми и темными точками. В одной из них выемки соответствуют центрам шариков предыдущего слоя, которые на рис. 19 справа видны как светло— серые треугольнички. Во второй выемки соответствуют выемкам предпредыдущего слоя и видны на рис. 19 справа как треугольнички с вписанными в них крохотными белыми шестиугольничками. Чтобы получить гранецентрированную кубическую решетку, мы должны использовать для третьего слоя темно-серые позиции, а затем повторять такой порядок укладки до бесконечности.

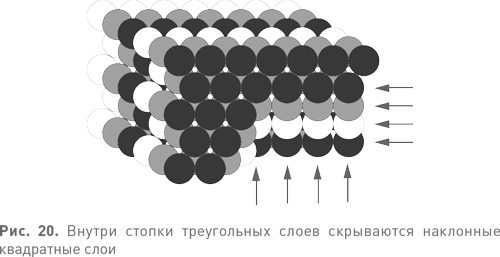
Не до конца очевидно, однако, что результатом такой укладки станет гранецентрированная кубическая решетка. Где же здесь квадраты? Дело в том, что квадраты в такой укладке присутствуют, но располагаются наклонно, под углом. На рис. 20 показаны шесть последовательных треугольных слоев, из которых удалена часть шариков. Стрелками указаны ряды и столбцы скрытой внутри квадратной решетки. Все слои, параллельные данному, тоже выстроены по квадратной решетке, а между собой соотносятся в точности так же, как я выстраивал гранецентрированную кубическую решетку.

Насколько компактна такая упаковка? Мы измеряем компактность (эффективность) упаковки ее плотностью: долей общего объема, занимаемой шариками. Чем больше плотность, тем компактнее упаковка. Кубики укладываются в параллелепипед с плотностью 1, заполняя весь объем. Между шариками, очевидно, в любом случае останутся промежутки, так что плотность их упаковки меньше единицы. Плотность гранецентрированной кубической решетки составляет в точности π/√18, это примерно 0,7405. При такой упаковке шарики заполняют чуть меньше трех четвертей пространства, и гипотеза Кеплера утверждает, что никакая упаковка шариков не может иметь плотность больше этой.

Я сформулировал все это достаточно осторожно. Я не сказал, что «плотность гранецентрированной кубической решетки выше, чем любой другой». Такое утверждение было бы неверным, и в этом несложно убедиться. Для этого вернемся к построению гранецентрированной кубической решетки из треугольных слоев. Я сказал, что после укладки первых двух слоев возникает два варианта укладки третьего. Гранецентрированная кубическая решетка возникает во втором варианте — том, что с темно-серыми точками. Что произойдет, если мы пойдем по первому пути и используем светло-серые точки? Тогда шарики третьего слоя окажутся точно над шариками первого. Продолжив точно так же и помещая каждый новый слой точно над позапрошлым слоем, мы получим второй вариант объемной решетки: гексагональную. Она отличается от гранецентрированной кубической решетки, но имеет ту же плотность. Интуитивно это понятно, поскольку два разных способа укладки третьего слоя симметричны относительно поворота, а сам слой в обоих случаях ложится на предыдущий одинаково плотно.

Это единственные два способа решетчатой упаковки, которые можно получить при укладке стопки треугольных слоев, но в 1883 г. географ и кристаллограф Уильям Барлоу заметил, что для каждого следующего слоя мы можем произвольно выбрать любой из двух вариантов укладки. Поскольку оба варианта вносят в плотность всей стопки одинаковый вклад, плотность всех этих вариантов упаковки будет одинакова и равна π/√18. При этом существуют бесконечно много случайных последовательностей такого рода и, соответственно, бесконечно много различных вариантов упаковки с одинаковой плотностью.

Короче говоря, нет единственной самой плотной объемной упаковки шариков. Их бесконечно много, и все они одинаково плотные. Отсутствие единственно верного решения — предупреждение: проблема не так проста и прямолинейна. Если Кеплер был прав, то существует оптимальная плотность упаковки, но есть и бесконечное множество различных структур, ею обладающих. И чтобы доказать оптимальность этой плотности, недостаточно успешно пристраивать каждый новый шарик к предыдущим как можно плотнее. Есть варианты.

Конечно, торговцы фруктами обладают невероятно богатым опытом — ведь гранецентрированную кубическую решетку наверняка можно было увидеть на рынках Древнего Египта еще в додинастическую эпоху, — но одним лишь опытом в таком деле никак не обойдешься. Вообще, тот факт, что метод торговцев фруктами дает хороший результат, в определенной мере случайность. Задача торговца фруктами состоит не в том, чтобы упаковать апельсины как можно плотнее в пространстве, где возможна, в принципе, любая конструкция. Его задача — уложить плоды как можно надежнее в мире, где земля плоская, а сила тяжести действует сверху вниз. Поэтому торговец начинает с того, что выкладывает апельсины в один слой — это очень естественно; затем он добавляет сверху еще один слой и т. д. Если ящик, в который укладываются плоды, прямоугольный, то первый слой, скорее всего, будет выложен по квадратной решетке. Если площадь ничем не ограничена, то естественной будет либо квадратная, либо треугольная решетка. В конечном итоге обе дают гранецентрированную кубическую решетку — по крайней мере, если треугольные слои укладываются как следует. Вообще говоря, квадратная решетка представляется не лучшим вариантом — ведь это не самый плотный способ укладки одного слоя. Однако — скорее по счастливой случайности, чем в результате осознанного выбора — это, как оказалось, не имеет значения.

Физики не интересуются апельсинами, их больше занимает то, как соседствуют друг с другом атомы. Кристалл — это регулярная, пространственно периодическая конструкция из атомов. Гипотеза Кеплера утверждает, что периодичность кристалла — это естественное следствие максимально плотной «упаковки» атомов. Для большинства физиков само существование кристаллов является достаточным доказательством, — по их мнению, гипотеза Кеплера очевидно верна. Однако мы только что убедились, что существует бесконечно много способов упаковки шариков с точно такой же плотностью, как у гранецентрированной кубической и гексагональной решеток, и что способы эти не являются пространственно периодическими. Так почему в кристаллах природа использует именно периодические структуры? Возможно, ответ в том, что атомы не следует рассматривать как сферические объекты.

Математики тоже не слишком интересуются апельсинами. Подобно Кеплеру, они предпочитают работать с идеальными и идентичными сферами, и доводы физиков не представляются им убедительными. Судите сами: если при моделировании кристаллов атомы не следует рассматривать как идеально круглые шарики, то существование кристаллов вообще не имеет отношения к гипотезе Кеплера и ничего не доказывает. Либо то, либо другое. Даже если вы скажете, что гипотеза как будто объясняет кристаллическую решетку, а кристаллическая решетка как будто показывает, что гипотеза верна… все равно в таком рассуждении будет логический пробел. Математикам нужно доказательство.

Кеплер не называл свое утверждение гипотезой: он просто высказал его в своей книге. Совершенно неясно, собирался ли он интерпретировать упомянутый факт столь всеобъемлющим образом. Имел ли он в виду, что гранецентрированная кубическая решетка представляет собой «самую плотную упаковку в трех измерениях» из всех представимых способов упаковки шариков? Или просто говорил о том, что это самая плотная упаковка из рассмотренных им лично? Невозможно вернуться в прошлое и спросить об этом. Но, как бы ни обстояло тогда дело, математиков и физиков интересует именно общая, самая смелая формулировка. Та, что требует рассмотреть все возможные способы упаковки бесконечного числа шариков в бесконечном пространстве и показать, что ни один из этих способов не может похвастать большей плотностью, чем гранецентрированная кубическая решетка.

Недооценить сложность гипотезы Кеплера очень легко. Вроде бы логично предположить, что самая плотная упаковка получится, если добавлять шарики по одному, так, чтобы каждый из них касался как можно большего числа соседних. Такой подход непременно даст структуру, о которой говорил Кеплер. То же получится, если вы будете добавлять шарики в правильном порядке и всегда, когда есть альтернативы, выбирать для них верную позицию. Однако нет никакой гарантии, что более дальновидная политика не окажется лучше, чем процесс поштучного добавления шариков. Всякий, кому приходилось укладывать вещи в багажник автомобиля, знает, что при укладке их по одной в багажнике могут остаться промежутки, куда ничего больше не лезет, но если начать сначала и подойти к вопросу более тщательно, то иногда удается втиснуть в то же пространство больше вещей. Конечно, отчасти проблема укладки вещей затрудняется тем, что все они имеют разные размеры и форму, но смысл аналогии достаточно понятен: максимально плотная упаковка на одном небольшом участке пространства может затруднить укладку остальных вещей и не привести к максимально плотной упаковке в большем объеме.

Конструкции, которые рассматривает Кеплер, очень специфичны. Можно предположить, что какой-то совершенно иной принцип позволит упаковать одинаковые шарики еще плотнее. Может быть, выпуклые слои были бы более эффективны. А может быть, «слои» — вообще неудачная идея. Но даже если вы абсолютно убеждены, что все сделано правильно, это все равно нужно доказывать.

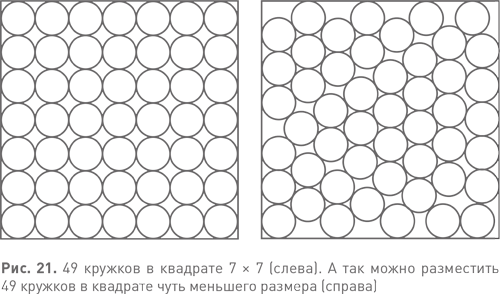
Не убеждены? По-прежнему считаете, что здесь все очевидно? Настолько очевидно, что никакого доказательства не требуется? Сейчас я попытаюсь разрушить вашу уверенность в правильности интуитивного решения — на более простом примере, где речь идет об укладке одинаковых кружочков на плоскости. Предположим, я дам вам 49 одинаковых кружочков единичного диаметра. Каким будет размер самого маленького квадрата, способного их все вместить без перекрытия? На рис. 21 слева показан очевидный ответ: расположить их, как ставят молочные бутылки в ящике. Сторона квадрата при этом — ровно 7 единиц. Чтобы убедиться, что это наилучший вариант, обратите внимание на то, что каждый кружок жестко удерживается остальными, так что лишнее место взять неоткуда. Но рис. 21 справа показывает, что этот ответ неверен. Стоит упаковать кружочки вот таким немного нерегулярным образом, и они поместятся в квадрате со стороной чуть меньше 6,98. Так что доказательство тоже неверно. Жесткость упаковки не гарантирует, что невозможно сделать плотнее.

Несложно убедиться, что рассуждения, позволяющие получить ответ «семь», просто не могут быть верными. Для этого достаточно рассмотреть квадрат побольше. Квадратная решетка позволяет поместить n² кружков единичного диаметра в квадрат со стороной n. Невозможно повысить плотность такой укладки путем плавного перемещения кругов, ведь укладка-то у нас жесткая. Но для больших n должны существовать и более плотные укладки, потому что, как известно, треугольная решетка эффективнее квадратной. Если взять по-настоящему большой квадрат и упаковать в него как можно больше кругов, используя треугольную решетку, то, в конце концов, треугольная решетка, благодаря своим преимуществам, победит, несмотря на «краевые эффекты» по границе квадрата, где придется оставлять незаполненные промежутки. Периметр квадрата — 4n — невелик по сравнению с n². Треугольная решетка одерживает верх над квадратной как раз при n = 7. Это не очевидно, и доказывать это пришлось бы долго и подробно, но ясно, что рано или поздно размер сработает. Одной только жесткости укладки недостаточно.

На самом деле существует два варианта гипотезы Кеплера. Одна рассматривает только регулярную упаковку; в ней центры шариков образуют пространственную периодическую структуру, которая бесконечно повторяется в трех независимых направлениях, как своего рода объемные обои. Даже в этом случае проблема весьма сложна, поскольку в пространстве возможно множество различных решеток. Кристаллографы различают 14 их типов, различаемых по видам симметрии, и некоторые из этих типов имеют параметры, которые могут принимать бесконечно много различных значений. Но все эти сложности меркнут, когда начинается рассмотрение второго варианта гипотезы, разрешающей любые возможные упаковки. Шарики здесь находятся в пространстве без гравитации и совершенно не обязаны собираться в слои или какие бы то ни было симметричные структуры.

Когда задача представляется слишком сложной, математики обыкновенно убирают ее в долгий ящик и принимаются искать более простые варианты. Рассуждения Кеплера о плоских слоях наводят на мысль о более простой задаче — упаковке кругов на плоскости. Это значит, что на плоскости, где имеется бесконечное число одинаковых кругов, надо собрать их как можно плотнее. В такой задаче плотность — это доля площади, которую покрывают круги. В 1773 г. Жозеф Луи Лагранж доказал, что самая плотная упаковка кругов на плоскости достигается в треугольной решетке, где плотность составляет π/√12 ≈ 0,9069. В 1831 г. Гаусс в отзыве на книгу Людвига Зибера (тот обобщил некоторые теоретические выводы Гаусса по уравнениям третьего порядка) отметил: результаты Зибера доказывают, что самую плотную регулярную упаковку в трехмерном пространстве обеспечивают гранецентрированная кубическая и гексагональная решетки. Сегодня математики очень много знают о решетчатой укладке в пространствах с бóльшим числом размерностей — четыре, пять, шесть и т. д. Особенно хорошо удалось разобраться с решетками в 24-мерном пространстве. (Да, такая уж это тема.) Несмотря на кажущуюся непрактичность, эта область математики имеет немало применений в теории информации и теории кодирования.

Нерешетчатые укладки — совершенно иное дело. Их бесконечно много, и они не отличаются приятной регулярностью структуры. Почему бы нам не удариться в другую крайность и не попробовать случайную укладку? Стивен Гейлс в своем труде «Статика растений» (1727) рассказал об экспериментах, в ходе которых он «вжимал несколько пакетов свежего гороха в один горшок» и обнаруживал, что при сильном сдавливании они образуют то ли «красивые правильные додекаэдры», то ли «достаточно правильные додекаэдры». Судя по всему, автор говорил о том, что правильные додекаэдры красивы, а не о том, что додекаэдры получались довольно правильные, но вторая интерпретация лучше, потому что настоящими правильными додекаэдрами невозможно без пустот заполнить пространство. Вероятно, он видел перед собой ромбические додекаэдры, которые, как мы уже убедились, связаны с гранецентрированной кубической решеткой. Дэвид Скотт насыпа́л в контейнер множество шариков от подшипников, тщательно встряхивал и измерял плотность укладки. По его данным, максимально она равнялась 0,6366. В 2008 г. Сун Чаомин, Ван Бин и Эрнан Макс получили эту же величину аналитически. Однако их результат не подразумевает, что Кеплер был прав, хотя бы потому, что это означало бы, что гранецентрированная кубическая решетка с плотностью 0,74 не может существовать. Простейшее объяснение такого расхождения заключается в том, что их результат не учитывает чрезвычайно редкие исключения, при том что и гранецентрированная кубическая, и гексагональная решетки, и все бесчисленные варианты конструкций из треугольных слоев представляют собой именно такие исключения. По тому же принципу может существовать и еще какая-нибудь конструкция с еще большей плотностью. Это не может быть регулярная конструкция, но найти ее при помощи бессистемного поиска невозможно, ибо ее вероятность равна нулю. Так что исследование случайных вариантов упаковки, хотя и важно для многих областей физики, не слишком много говорит нам о гипотезе Кеплера.

Первый по-настоящему важный прорыв в решении этой задачи произошел в 1892 г., когда Аксель Туэ в ходе лекции на Скандинавском конгрессе естественных наук коротко изложил доказательство того, что никакая упаковка кругов на плоскости не может быть плотнее треугольной решетки. Лекция была опубликована, но формулировки там слишком неопределенны, чтобы можно было реконструировать само доказательство. Новую версию того же доказательства Туэ опубликовал в 1910 г. Оно казалось убедительным, за исключением нескольких технических моментов, которые, как считал автор, можно было без особого труда довести до ума. Но Ласло Фейеш Тот, вместо того чтобы заполнять пробелы в чужом доказательстве, получил в 1940 г. собственное, полное, основанное на других методах. Вскоре после этого Беньямино Сегре и Курт Малер представили альтернативные доказательства. А в 2010 г. Чан Хайчау и Ван Личун выложили в Интернет более простое доказательство.

Задача поиска наибольшей плотности укладки кругов или шариков при определенных условиях относится к классу математических задач, известных как задачи оптимизации. В такой задаче предлагается найти максимальное или минимальное значение некоторой функции (т. е. математического правила вычисления некой величины, которая определенным образом зависит от некоего набора переменных). Правило вычисления функции часто задается формулой, но это не обязательно. К примеру, таким образом можно сформулировать задачу с 49 кругами на плоскости. Переменными здесь будут координаты центров всех 49 кругов, а поскольку на каждый круг потребуется по две координаты, всего переменных получится 98. Сама функция — это размер наименьшего квадрата со сторонами, параллельными координатным осям, в который можно поместить данный набор неперекрывающихся кругов. Задача эквивалентна поиску минимального значения, которое принимает эта функция при значениях переменных, соответствующих всем вариантам решетки.

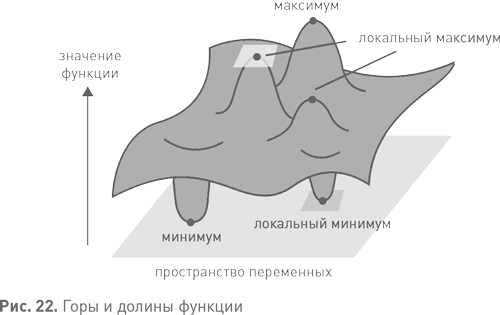
Функцию можно представить в виде многомерного ландшафта, каждая точка на котором соответствует определенному набору переменных, а высота в этой точке — значению функции. Максимум функции — это высота самого высокого ее пика, а минимум — глубина самой глубокой долины. В принципе задачи оптимизации можно решать методами дифференциального исчисления: в максимуме или минимуме функция должна быть горизонтальна (см. рис. 22), и дифференциальное исчисление позволяет отразить это условие в уравнении. Чтобы решить задачу укладки кругов в квадрат этим методом, нам пришлось бы решить систему из 98 уравнений с 98 переменными.

Решение задач оптимизации встречает на пути одно неожиданное препятствие: подобные уравнения часто имеют большое количество решений. Ландшафт может иметь множество локальных максимумов, из которых самый высокий лишь один. Представьте себе, к примеру, Гималаи: кроме пиков, там почти ничего и нет, но лишь Эвересту принадлежит рекорд высоты. Методы поиска пиков, самый очевидный из которых звучит как «иди вверх, пока это возможно», часто выводят на локальные максимумы и застревают на них. Еще одна трудность состоит в том, что с ростом числа переменных растет и вероятное число локальных пиков. Тем не менее иногда такой метод срабатывает. Даже частичные результаты могут оказаться полезными: если вам удалось найти локальный пик, ясно, что настоящий максимум не может быть ниже. Именно так была найдена улучшенная раскладка кругов в квадрате.

Для регулярных укладок функция, максимум которой нужно найти, зависит от конечного числа переменных — направлений и длин, вдоль которых решетка повторяется. Для нерегулярных укладок функция зависит от бесконечно большого числа переменных — центров всех кругов или шариков. В подобных случаях прямое использование дифференциального исчисления и других методик оптимизации ничего не даст. Доказательство Тота основано на хитрой идее переформулировать задачу о нерегулярной упаковке кругов и превратить ее в задачу оптимизации с конечным набором переменных. Позже, в 1953 г., он понял, что тот же трюк в принципе можно проделать и с гипотезой Кеплера. К несчастью, получившаяся функция зависит примерно от полутора сотен переменных — слишком много для ручного расчета. Но Тот прозорливо разглядел возможный выход: «Имея в виду стремительное развитие наших компьютеров, можно предположить, что минимум можно будет определить с высокой точностью».

В то время вычислительная техника только начинала развиваться, и достаточно мощной машины попросту не существовало, так что в последующие годы работа над гипотезой Кеплера шла в других направлениях. Ряд математиков занимался уточнением верхней границы для возможного значения плотности сферической упаковки. К примеру, в 1958 г. Роджерс доказал, что плотность не превосходит 0,7797. И никаких исключений: эта оценка относилась к любым способам укладки шариков. В 1986 г. Дж. Линдси понизил этот предел до 0,77844, а Дуглас Мадер в 1988 г. чуть-чуть улучшил оценку и получил 0,77836. Эти результаты показали, что невозможно получить плотность намного выше, чем 0,7405, характерные для гранецентрированной кубической решетки. Но тем не менее пробел в доказательстве сохранялся.

В 1990 г. американский математик Ву-И Хзянь объявил, что гипотеза Кеплера доказана. Подробности были опубликованы, но сразу появились сомнения. Тот, просмотрев статью в журнале Mathematical Reviews, написал: «Если бы спросили меня, [доказана ли тем самым гипотеза Кеплера] я бы ответил: нет. Надеюсь, что Хзянь дополнит свое сообщение, но мне кажется, что значительная часть работы еще впереди».

Томас Хейлс, посвятивший работе над гипотезой много лет, тоже высказал сомнения в том, что метод Хзяня можно довести до ума. Вместо этого он решил, что настало время всерьез отнестись к подходу, предложенному Тотом. Выросло новое поколение математиков, для которых естественнее обратиться к компьютеру, чем к таблице логарифмов. В 1996 г. Хейлс обрисовал стратегию доказательства, основанную на идее Тота. Эта стратегия требовала определить все возможные способы организации шариков в непосредственной близости от данного шарика. Укладка шариков определяется центрами соответствующих сфер. Для единичных сфер расстояние между центрами должно составлять по крайней мере две единицы. Скажем, что два шарика являются соседями, если их центры разделены расстоянием не более 2,51 единицы. Этот предел следует установить аккуратно: при слишком маленьком расстоянии не хватит места для перестановки шариков и повышения плотности, а при слишком большом количество вариантов расстановки соседних шариков станет просто гигантским. Хейлс выяснил, что 2,51 — это эффективный компромисс. Теперь мы можем представить, как располагаются шарики-соседи, и построить в пространстве бесконечную сеть. Узлами в ней станут центры шариков, а соединяться между собой линиями они будут, если соответствующие шарики — соседи. Эта сеть — своеобразный скелет укладки — содержит всю существенную информацию о соседях каждого шарика.

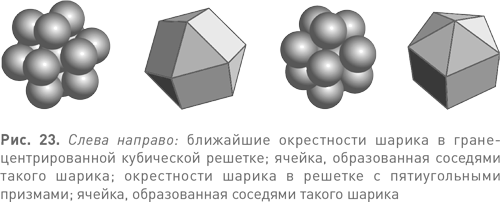
Для любого шарика мы можем взять непосредственно соседствующие с ним шарики и рассматривать далее только линии между ними, исключив сам первоначальный шарик. В результате получим своего рода клетку, или ячейку, вокруг точки в центре первоначальной сферы. На рис. 23 показаны: (левая пара) соседи шарика в гранецентрированной кубической решетке и соответствующая ячейка; (правая пара) то же самое для особой структуры из шариков — пятиугольной призмы; эта структура оказалась ключевым игроком всего доказательства. Вы видите здесь два плоских пятиугольника, параллельные «экватору» центрального шарика и еще по шарику на каждом полюсе конструкции.

Ячейку можно изобразить как твердое тело с плоскими гранями; при этом плотность укладки вблизи центрального шарика будет определяться геометрией этого тела. Ключевая идея состоит в том, чтобы каждой ячейке поставить в соответствие некое число (назовем его мерой ячейки), которое станет способом оценки плотности упаковки соседей центрального шарика. Мера ячейки — это не собственно плотность; это величина, которая ведет себя лучше и вычисляется проще плотности. В частности, меру ячейки можно найти просто как сумму мер ее граней; с плотностью такой метод не работает. В принципе, множество разных определений меры соответствуют этому условию, но все они сходятся в одном: для гранецентрированной кубической и гексагональной решеток мера, как бы вы ее ни определяли, всегда составляет восемь пунктов. В данном случае пункт равняется вполне конкретному числу:

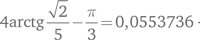
Так что восемь пунктов на самом деле равняются 0,4429888. Это занятное число вычисляется исходя из особой геометрии гранецентрированной кубической решетки. Ключевое наблюдение Хейлса связывает гипотезу Кеплера с этим числом: если любая ячейка имеет меру восемь или меньше, гипотеза Кеплера верна. Таким образом, фокус доказательства смещается на ячейки и их меры.

Ячейки можно классифицировать по топологии: сколько у них имеется граней с тем или иным числом сторон и как эти грани сочетаются друг с другом. Однако при любой заданной топологии стороны граней ячейки могут быть различной длины. Длина сторон влияет на меру, но топология соединяет множество разных ячеек, и их можно рассматривать в общем. В своем доказательстве Хейлс рассмотрел около 5000 типов ячеек, но основные расчеты велись по нескольким сотням вариантов. В 1992 г. он предложил проект доказательства из пяти этапов:

1. Доказать утверждение в случае, когда все грани ячейки представляют собой треугольники.

2. Показать, что гранецентрированная кубическая и гексагональная укладки имеют более высокую меру, чем любая ячейка с той же топологией.

3. Разобраться со случаем, когда все грани ячейки представляют собой треугольники и четырехугольники, за исключением пятиугольной призмы (это более сложный случай).

4. Разобраться с ячейками, грани которых имеют более четырех сторон.

5. Разобраться с единственным оставшимся случаем — с ячейкой в виде пятиугольной призмы.

Часть 1 была реализована в 1994 г., часть 2 — в 1995 г. По ходу программы Хейлс модифицировал определение ячейки так, чтобы упростить рассуждения (он использовал термин «звезда декомпозиции»). Новое определение не изменило две представленные ячейки и почти не затронуло те части доказательства, которые были уже реализованы. К 1998 г. при помощи новой концепции были завершены все пять предложенных Хейлсом этапов. Часть 5 — хитрый случай с пятиугольной призмой — рассмотрел студент Хейлса Сэмюел Фергюсон.

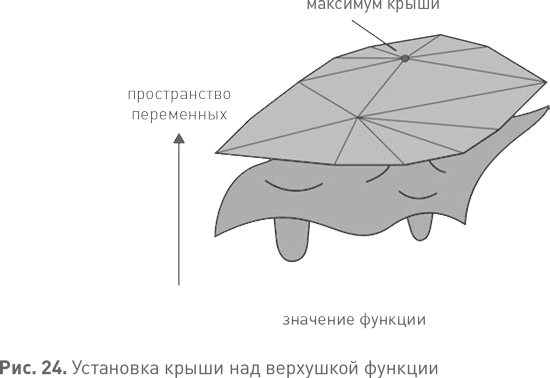
На всех этапах анализа были масштабно задействованы компьютеры. Хитрость здесь в том, чтобы для каждой локальной сети выбрать такое представление о мере, которое сделало бы вычисления сравнительно несложными. Геометрически замена плотности на меру выглядит как сооружение своеобразной крыши над гладким ландшафтом, максимум которого ищет исследователь. Крыша состоит из нескольких плоских участков (см. рис. 24). Работать с такими формами значительно легче, чем с гладкими поверхностями, поскольку максимумы располагаются в углах, для нахождения которых достаточно решить куда более простые уравнения. Для этого существуют эффективные методы, известные как линейное программирование. Если крыша построена так, что ее пик совпадает с пиком гладкой поверхности, то более простые расчеты, предназначенные для поисков пика крыши, позволят найти не только его, но и пик гладкой поверхности.

У всякого упрощения есть своя цена, и у этого тоже: чтобы найти пик крыши, приходится решать около 100 000 линейных задач. Впрочем, достаточно длинные расчеты, необходимые для этого, вполне по силам современным компьютерам. Когда Хейлс и Фергюсон подготовили свою работу к публикации, в ней оказалось около 250 страниц математического текста и 3 Гбайт компьютерных файлов.

В 1999 г. Хейлс подал подготовленное доказательство в Annals of Mathematics, и журнал специально для этого случая набрал жюри из 12 экспертов. К 2003 г. оно объявило, что «с уверенностью на 99 %» представленное доказательство верно. Оставшийся 1 % неуверенности касался компьютерных расчетов; многие из них жюри повторило, а также иными способами проверило стратегию и тактику доказательства, но некоторые его аспекты проверить не удалось. После значительной задержки журнал опубликовал работу. Хейлс признал, что такой подход к доказательству, вероятно, никогда не будет признан на 100 % корректным, и в 2003 г. объявил о старте проекта по переформатированию доказательства в такой вид, в котором его сможет проверить компьютер при помощи стандартных программ автоматической проверки доказательств.

Это может показаться чем-то вроде перехода из огня в полымя, но на самом деле все предельно понятно и логично. Доказательства, которые математики публикуют в журналах, призваны убеждать людей. Как я уже говорил в главе 1, доказательство — это своего рода рассказ. Компьютеры не сильны в литературе, зато прекрасно справляются с заданиями, которые нам не по зубам: они способны безошибочно выполнять длинные нудные расчеты. Компьютеры идеально сочетаются с формальным определением доказательства в университетских учебниках: серия логических шагов, каждый из которых вытекает из предыдущих.

Компьютерщики научились использовать эту способность. Чтобы проверить доказательство, заставьте компьютер проанализировать каждый логический шаг. Звучит просто, но на самом деле доказательства в журналах пишут не так. Эти рассказы оставляют за скобками все рутинное или очевидное… Все привыкли к традиционным фразам: «Несложно убедиться, что…», «Используя методы Чизбургера и Чипса, модифицированные так, чтобы учитывать изолированные сингулярности, видим, что…», «Несложный расчет показывает…». Компьютеры (пока) с подобными задачами не справляются. Но люди-то всегда могут переписать доказательство, заполнив все подобные пропуски, и тогда компьютер вполне может проверить каждый его шаг.

Мы не прыгаем сразу же обратно в огонь по одной простой причине: программы, которые проверяют доказательство, тоже необходимо проверить, но лишь один раз. Вообще-то это универсальное программное обеспечение, которое применимо к любому доказательству, записанному в надлежащем формате. Все, что может вызывать сомнения, сконцентрировано здесь. Проверьте его — и потом с его помощью можно проверять все остальное. Можно даже упростить себе работу, написав программу проверки доказательства на языке, который позволит проверить ее при помощи гораздо более простой программы проверки.

В последние годы таким образом были проверены доказательства многих ключевых математических теорем. Для этого их нередко требовалось перевести в другую форму, более подходящую для компьютерных манипуляций. Один из последних триумфов — проверка и подтверждение доказательства теоремы Жордана: всякая замкнутая кривая без самопересечений на плоскости делит плоскость на две связные области. Утверждение может показаться очевидным, но пионеры топологии долго не могли строго доказать его. В конце концов это удалось в 1887 г. Камилю Жордану, опубликовавшему доказательство на 80 страницах, но позже его нередко критиковали за необоснованные ограничения. Поэтому слава досталась Освальду Веблену, давшему в 1905 г. более подробное доказательство. Веблен заявил: «[Жорданово] доказательство… не удовлетворяет многих математиков. В нем теорема принимается без доказательства в существенном особом случае, когда речь идет о простом многоугольнике; что же касается дальнейшего изложения, то следует признать по крайней мере, что не все детали в нем приведены».

Математики без колебаний приняли критику Веблена, но недавно Хейлс еще раз проанализировал доказательство Жордана и не нашел в нем «ничего, на что можно было бы возразить». Более того, замечание Веблена о многоугольнике звучит странно: теорема для него достаточно прозрачна, да и доказательство Жордана вовсе не опирается на этот частный случай. У доказательств-рассказов есть собственные проблемы. С ними надо держать ухо востро и проверять, совпадает ли популярная версия рассказа с его оригинальным вариантом.

В процессе работы над гипотезой Кеплера Хейлс получил в 2007 г. формальное, проверенное компьютером доказательство теоремы Жордана, на что потребовалось 60 000 строк компьютерного кода. Вскоре после этого группа математиков, воспользовавшись другим программным обеспечением, получила другое формальное доказательство. Компьютерная проверка не застрахована от ошибок на 100 %, но то же можно сказать и о традиционных доказательствах. Более того, многие математические научные труды, вероятно, содержат технические ошибки. Время от времени такие ошибки обнаруживаются и в большинстве случаев оказываются безвредными. Серьезные ошибки, как правило, замечают раньше, чем они приводят к нарушениям и делают что-то явно бессмысленным. Это еще один недостаток доказательства-рассказа — плата за то, что доказательство делается понятным человеку: иногда нестрогая логика выглядит на первый взгляд очень убедительно.

Хейлс называет свой подход Project FlysPecK. Согласно первоначальной оценке, работа над ним должна была занять около 20 лет. За первые девять лет достигнут очень существенный прогресс, так что проект может завершиться досрочно.