9. Закономерности простых чисел. Гипотеза Римана

В главе 2 мы рассматривали индивидуальные свойства простых чисел, и я сравнил их с зачастую непоследовательным и непредсказуемым поведением людей. Но люди обладают свободой воли, они могут принимать решения, исходя из своих соображений. А простые числа делают то, что подсказывает им логика арифметики, хотя нередко создается впечатление, что они тоже обладают собственной волей. Их поведение управляется странными совпадениями и часто лишено какой бы то ни было разумной структуры.

Тем не менее в мире простых чисел не правит анархия. В 1835 г. Адольф Кетле поразил современников, обнаружив математические закономерности в мире социальных явлений, которые зависят от сознательных решений разных людей или вмешательства судьбы: в мире рождений, свадеб, смертей, самоубийств. Закономерности были статистическими и касались не отдельных людей, а усредненного поведения больших человеческих масс. Именно так статистики извлекают порядок из индивидуальной свободы воли. Примерно в то же время математики начали осознавать, что такой фокус можно проделать и с простыми числами. Пусть каждое из них в отдельности — ярый индивидуалист, все вместе они подчиняются закону. Существуют скрытые закономерности.

Статистические закономерности проявляются тогда, когда мы рассматриваем сразу все множество простых чисел. К примеру: сколько простых чисел содержится в натуральном ряду до некоего определенного предела? На этот вопрос очень сложно ответить точно, но существуют прекрасные аппроксимации, и чем выше предел, тем точнее становятся приближенные значения. Иногда можно добиться, чтобы разница между приближенным и точным ответами была очень мала, но, как правило, это означало бы хотеть слишком многого. Большинство приближений в этой области являются асимптотическими. Это означает, что отношение приближенного значения к точному можно сделать очень близким к 1. При этом, хотя ошибка в процентах стремится к нулю, абсолютная ошибка может быть сколь угодно велика.

Если вы пытаетесь понять, как такое может быть, представим последовательность чисел — для некоего трудного для понимания свойства простых чисел — состоящую из степеней 100:

Но реальные числа при этом таковы:

т. е. лишняя единица сдвигается на каждом шаге влево на одну позицию. В этом случае отношение соответствующих чисел, чем дальше, тем ближе подходит к 1, а вот разность между ними приобретает вид:

и может достигать сколь угодно больших значений. Подобное поведение наблюдается в тех случаях, когда ошибка — разность между точным и приближенным ответом — беспредельно растет, но медленнее, чем растут сами числа.

Поиск асимптотических формул, имеющих отношение к простым числам, вдохновил математиков на создание новых методов теории чисел, основанных не на целых числах, а на комплексном анализе. Анализ — это строгое описание дифференциального и интегрального исчисления, включающего, как явствует из названия, два ключевых аспекта. В первом из них — дифференциальном исчислении — речь идет о скорости, с которой некая величина, называемая функцией, растет по отношению к другой величине. К примеру, положение тела зависит от времени, и скорость, с которой это положение изменяется со временем, представляет собой мгновенную скорость тела. Второй аспект — интегральное исчисление — имеет дело с расчетом площадей, объемов и тому подобных величин путем складывания большого числа очень маленьких кусочков. Процесс этот называется интегрированием. Примечательно, что интегрирование — это операция, обратная дифференцированию. Первоначальные формулировки Ньютона и Готфрида Лейбница требовали некоторых маневров с бесконечно малыми величинами, в связи с чем возникали вопросы о логической обоснованности этой теории. Со временем ученые разобрались с этими концептуальными вопросами, определив понятие предела — величины, к которой можно приблизиться на сколь угодно малое расстояние, но которой зачастую невозможно достичь. Именно в таком виде, в более строгих формулировках, метод получил название анализа.

Во времена Ньютона и Лейбница величины, о которых шла речь, представляли собой действительные числа, и результатом их работы, соответственно, стал действительный анализ. Когда же комплексные числа завоевали признание математиков, методы анализа естественным образом распространили и на них. Получился комплексный анализ, оказавшийся необычайно красивым и мощным инструментом. Вообще, когда дело доходит до анализа, комплексные функции ведут себя намного лучше, чем действительные. У них, конечно, есть свои особенности, но преимущества работы с комплексными функциями многократно перевешивают все их недостатки.

В какой-то момент математики с удивлением обнаружили, что арифметические свойства целых чисел можно с большой пользой переформулировать в терминах комплексных функций. До этого две системы ставили перед учеными очень разные вопросы и требовали использования очень разных методов. Но сегодня при помощи комплексного анализа — мощнейшего набора методик — можно открывать особые свойства функций теории чисел, а из них, в свою очередь, можно извлекать асимптотические формулы и многое другое.

В 1859 г. немецкий математик Бернхард Риман взял давнюю идею Эйлера и развил ее совершенно по-новому, определив так называемую дзета-функцию. Одним из результатов этой работы стала точная формула для количества простых чисел до заданного предела. Формула представляла собой бесконечную сумму, но специалистам по анализу к этому не привыкать. И это не было бесполезной игрой ума: благодаря этой формуле удалось получить новые подлинные знания о мире простых чисел. Мешала только одна маленькая неувязка. Хотя Риман мог доказать, что его формула точна, самые важные потенциальные следствия из нее полностью зависели от одного простого утверждения, касающегося дзета-функции, и вот это-то простое утверждение Риман никак не мог доказать. И сегодня, полтора столетия спустя, мы все еще не сумели сделать это. Сегодня это утверждение называется гипотезой Римана и представляет собой, по сути, священный Грааль чистой математики.

В главе 2 мы видели, что простые числа обыкновенно встречаются тем реже, чем они больше. Поскольку казалось, что точных формул для их распределения наверняка не существует, возникало естественное желание поискать статистические закономерности. В 1797–1798 гг. Лежандр подсчитал, сколько простых чисел помещается в натуральном ряду вплоть до различных пределов. Для этого он воспользовался таблицами простых чисел, которые незадолго до того составили Георг Вега и Антон Фелькель. Веге, судя по всему, вообще нравились сложные расчеты: он составил таблицы логарифмов и в 1789 г. стал обладателем мирового рекорда по вычислению числа π, которое он посчитал до 140-го десятичного знака (из них 126 были посчитаны верно). А Фелькелю просто нравилось искать простые числа. Его главная работа вышла в 1776 г. и называлась «Таблица всех простых делителей чисел до 10 000 000, за исключением тех, что делятся на 2, 3 или 5». Для проверки делимости на 2, 3 и 5 есть простые способы, упомянутые в главе 2, и он сэкономил в книге много места, опустив эти числа. Лежандр открыл эмпирическую приближенную формулу для количества простых чисел, меньших заданного числа x, и обозначил это количество π(x). Если вы привыкли воспринимать π только как символ для обозначения числа 3,14159, это потребует привыкания, но в любом контексте несложно понять, что именно имелось в виду, даже если вы не заметили, что символы даны в несколько разном начертании. В 1808 г. в тексте Лежандра по теории чисел утверждалось, что значение π(x), судя по всему, очень близко к значению выражения x/(log x − 1,08366).

В 1849 г. в письме к астроному Иоганну Энке Гаусс сообщил, что в свое время, лет в 15, сделал на полях таблицы логарифмов запись, в которой утверждалось количество простых чисел, меньших или равных x, составляет x/log x для больших x. Гаусс не опубликовал это наблюдение (как и многие другие свои открытия), возможно, потому, что не имел доказательства. В 1838 г. Дирихле сообщил Гауссу об аналогичной приближенной формуле, найденной им самим. По существу, эта формула сводится к логарифмической интегральной функции

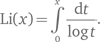
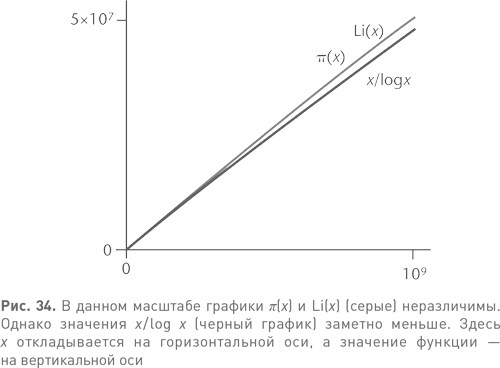
По мере того как x становится большим, отношение Li(x) к x/log x стремится к 1; это означает, что если одно из них асимптотически равно π(x), то асимптотически равно и второе, но рис. 34 позволяет предположить (совершенно верно), что Li(x) — лучшее приближение, чем x/log x. Точность Li(x) впечатляет. К примеру,

Аппроксимация в виде x/log x хуже: в данном случае ее значение 48 254 942,4.

Приближенная формула с использованием Li(x) или x/log x стала известна как теорема о распределении простых чисел, где слово «теорема» использовалось в смысле «предположение». Поиск доказательства того, что эти формулы асимптотичны к π(x), стал одной из ключевых открытых задач теории чисел. Многие математики пытались одолеть ее при помощи традиционных методов этой области науки, и некоторые подошли к ответу достаточно близко, однако всегда оставалась какая-то хитрая посылка, которую никак не удавалось доказать. Нужны были новые методы. Они появились в результате любопытного переформулирования двух древних, еще евклидовых, теорем о простых числах.

Теорема о распределении простых чисел была ответом на евклидову теорему о том, что простые числа уходят в бесконечность и могут быть сколь угодно большими. Другая фундаментальная евклидова теорема говорит о единственности разложения на простые множители: каждое положительное целое число есть произведение простых чисел, причем только одного их набора. В 1737 г. Эйлер понял, что первую теорему можно переформулировать в виде поразительной формулы из действительного анализа, и тогда второе утверждение становится простым следствием этой формулы. Для начала я представлю формулу, а затем попытаюсь разобраться в ней. Вот она:

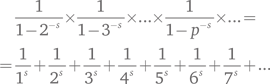
Здесь p принимает все простые значения, а s — константа. Эйлера интересовал в основном случай, при котором s — целое число, но его формула работает и для действительных чисел, в случае если s больше единицы. Это условие необходимо для того, чтобы ряд в правой части сошелся, т. е., будучи продолжен до бесконечности, принял бы осмысленное значение.

Это необыкновенная формула. В левой части мы перемножаем бесконечно много выражений, которые зависят только от простых чисел. В правой — складываем бесконечное число выражений, которые зависят от всех положительных целых чисел. Эта формула выражает, на языке анализа, некоторое отношение между целыми и простыми числами. Главное отношение такого рода — это единственность разложения на простые множители, именно она оправдывает существование формулы.

Я кратко опишу основной этап, чтобы показать, что за всем этим стоит разумная идея. Воспользовавшись школьной алгеброй, мы можем разложить выражение в ряд по p. Этот ряд напоминает правую часть формулы, но включает только степени p. А именно:

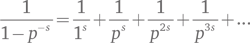
Когда мы перемножим все эти ряды, для всех простых p, и раскроем все скобки, мы получим комбинации с любыми степенями простых чисел, т. е. с любыми целыми положительными степенями. Все они выглядят как величины, обратные (т. е. единица, деленная на) s-й степени данного числа, и все возникают лишь единожды в связи с единственностью разложения на простые множители. Таким образом, получаем ряд в правой части.

Никому до сих пор не удалось найти простой алгебраической формулы для суммы этого ряда, хотя формул с интегралами немало. Поэтому мы присвоили ей особый символ — греческую букву дзета (ζ) — и определили новую функцию:

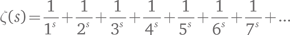
Вообще говоря, Эйлер не использовал символ ζ и рассматривал только положительные целые значения s, но я буду и дальше называть приведенный выше ряд эйлеровой дзета-функцией. Воспользовавшись своей формулой, Эйлер заключил, что существует бесконечно много простых чисел (для этого он рассматривал значения s, близкие к единице). Главной его целью было получить формулы вроде ζ (2) = π²/6 и найти сумму ряда для четных целых s. Развивать свою революционную идею дальше он не стал.

Другие математики заметили упущение Эйлера и рассмотрели нецелые значения s. В двух работах 1848 и 1850 гг. русский математик Пафнутий Чебышев предложил великолепную идею: попытаться доказать теорему о распределении простых чисел при помощи анализа. Начал он со связи между простыми числами и математическим анализом, обеспечиваемой эйлеровой дзета-функцией. Он не добился полного успеха, поскольку считал s действительным числом, а аналитические возможности действительного анализа весьма ограничены. Зато он сумел доказать, что для больших x отношение π(x) к x/log x лежит между двумя константами, одна из которых чуть больше единицы, а вторая — чуть меньше. Это был уже реальный результат, хотя пока еще не такой, как хотелось. Он позволил Чебышеву доказать постулат Бертрана, предложенный в 1845 г.: если взять любое натуральное число (≥2) и удвоить его, то между двумя этими числами обязательно найдется простое число.

Вот теперь сцена была готова к появлению Римана. Он тоже понял, что дзета-функция — это ключ к теореме о распределении простых чисел, но для реализации этого подхода ему пришлось предложить смелое расширение: определить дзета-функцию не только действительной, но и комплексной переменной. А начать можно с ряда Эйлера. Он сходится для любых действительных s больше единицы, и если использовать для комплексного s в точности ту же формулу, то ряд будет сходиться при любых s, у которых действительная часть больше 1. Однако Риман обнаружил, что можно сделать и лучше. Применив процедуру так называемого аналитического продолжения, он расширил определение ζ (s) на все комплексные числа, за исключением 1. Это значение s исключено потому, что при s = 1 значение дзета-функции становится бесконечным.

В 1859 г. Риман собрал все свои мысли о дзета-функции в одну статью, заголовок которой можно перевести как «О количестве простых чисел, не превышающих заданной величины». В ней он привел полную и точную формулу π(x). Я опишу более простую формулу, эквивалентную римановой, чтобы показать, как появляются нули дзета-функции. Идея заключается в том, чтобы подсчитать, сколько простых чисел, или степеней простых чисел, укладывается до любого заданного предела. Однако вместо того чтобы сосчитать каждое число по одному разу, как функция π(x) делает с простыми числами, мы придаем большим простым числам дополнительный вес. Более того, любая степень простого числа учитывается в соответствии с логарифмом этого простого числа. Так, для предела 12 мы имеем следующие степени простых чисел:

поэтому взвешенный подсчет дает

что составляет примерно 10,23.

Воспользовавшись методами анализа, информацию об этом более хитроумном способе подсчета простых чисел можно превратить в информацию об обычном способе. Однако этот метод приводит к более простым формулам, и присутствие логарифма — не слишком дорогая цена за это. В этих терминах точная формула Римана говорит о том, что взвешенный подсчет до предела x эквивалентен

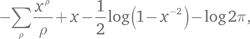
где Σ обозначает сумму по всем числам ρ, для которых ζ(ρ) равна нулю, исключая отрицательные четные целые числа. Эти значения называются нетривиальными нулями дзета-функции. Тривиальные нули — это отрицательные четные целые числа −2, −4, −6… Во всех этих точках дзета-функция равняется нулю из-за формулы, которая используется в определении аналитического продолжения, но, как выяснилось, для римановой формулы эти нули несущественны (как и почти везде в других местах).

На случай, если формула вас немного пугает, я укажу главное: хитрый способ подсчета простых чисел до заданного предела x, который при помощи кое-каких аналитических фокусов можно превратить в обычный способ, в точности эквивалентен сумме по всем нетривиальным нулям дзета-функции простого выражения xρ/ρ плюс некая несложная функция от x. Если вы специалист по комплексному анализу, вы сразу увидите, что доказательство теоремы о распределении простых чисел эквивалентно доказательству того, что взвешенный подсчет до предела x асимптотически сходится к x. Воспользовавшись комплексным анализом, получим: это утверждение верно, если у всех нетривиальных нулей дзета-функции действительная часть лежит между 0 и 1. Чебышев не смог этого доказать, но подошел достаточно близко, чтобы извлечь полезную информацию.

Почему нули дзета-функции так важны? Одна из базовых теорем комплексного анализа утверждает, что при некоторых формальных условиях функция комплексной переменной полностью определяется значениями переменной, при которых функция равна нулю или бесконечности, плюс некоторая дополнительная информация о поведении функции в этих точках. Эти особые точки известны как нули и полюсы функции. В действительном анализе эта теорема не работает — и это одна из причин, по которым комплексный анализ завоевал такую популярность, несмотря на необходимость извлекать корень квадратный из −1. У дзета-функции один полюс (при s = 1), так что все ее характеристики определяются нулями (если, конечно, не забывать о существовании этого единственного полюса).

Для удобства Риман работал в основном с зависимой кси-функцией ξ (x), которая тесно связана с дзета-функцией и получается из метода аналитического продолжения. Он заметил:

Это заявление о кси-функции эквивалентно аналогичному заявлению о зависимой от нее дзета-функции. А именно: все нетривиальные нули дзета-функции представляют собой комплексные числа вида: они лежат на критической линии «действительная часть равна 1/2» (см. рис. 35). Эта версия замечания и есть знаменитая гипотеза Римана.

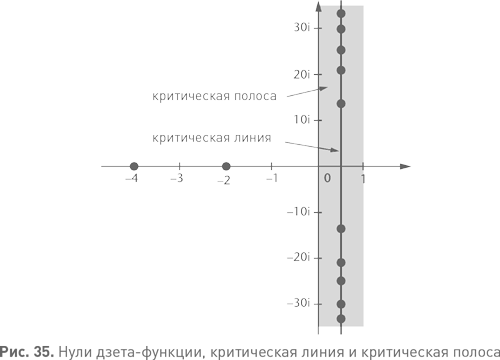
Замечание Римана звучит достаточно небрежно, как будто высказано между делом и эта гипотеза не имеет особого значения. И это действительно так, если говорить только о программе Римана по доказательству теоремы о распределении простых чисел. Но во многих других вопросах верно обратное. Многие считают гипотезу Римана важнейшим из остающихся на сегодняшний день открытыми математических вопросов.

Чтобы понять, почему это так, мы должны последовать за рассуждениями Римана чуть дальше. В тот момент ученый был нацелен на теорему о распределении простых чисел. Его точная формула предлагала верный путь к этому достижению: нужно было разобраться в нулях дзета-функции или эквивалентной ей кси-функции. Полная риманова гипотеза для этого не нужна, достаточно доказать, что у всех нетривиальных нулей дзета-функции действительная часть лежит в промежутке от 0 до 1, т. е. что сами комплексные корни лежат на расстоянии не более 1/2 от римановой критической линии — в так называемой критической полосе. Это свойство нулей подразумевает, что сумма по всем нулям дзета-функции, фигурирующая в приведенной выше точной формуле, представляет собой конечную константу. Асимптотически для больших x она вообще может потеряться. Единственный член формулы, который сохранит свое значение при очень больших x, это сам x. Все остальные сложные слагаемые асимптотически пропадают в сравнении с x. Следовательно, взвешенная сумма асимптотически стремится к x, и это доказывает теорему о распределении простых чисел. Так что, по иронии судьбы, роль нулей дзета-функции заключается в том, чтобы доказать, что они не вносят существенного вклада в точную формулу.

Риман так и не довел свою программу до логического конца. Более того, он никогда больше ничего не писал по этому вопросу. Но два других математика, приняв у него эстафету, показали, что догадка Римана верна. В 1896 г. Жак Адамар и Шарль-Жан де ла Валле Пуссен независимо друг от друга вывели теорему о распределении простых чисел, доказав, что все нетривиальные нули дзета-функции лежат в пределах критической полосы. Доказательства у обоих получились очень сложными и техничными, но тем не менее свою задачу они выполнили. Возникла новая мощная область математики — аналитическая теория чисел. Применение ей нашлось в самых разных уголках теории чисел: с ее помощью решали давние задачи и выявляли новые закономерности. Другие математики позже нашли несколько более простых доказательств теоремы о числе простых, а Атле Сельберг и Пал Эрдеш открыли даже очень сложное доказательство, вовсе не требовавшее применения комплексного анализа. Но к тому моменту при помощи идеи Римана было доказано бесчисленное множество важных теорем, включая аппроксимации многих функций теории чисел. Так что это новое доказательство хоть и добавило в эту историю каплю иронии, но ни на что, в сущности, не повлияло. В 1980 г. Дональд Ньюман нашел гораздо более простое доказательство, для которого достаточно оказалось всего лишь одной из самых базовых теорем комплексного анализа — теоремы Коши.

Хотя Риман объявил свою гипотезу ненужной для достижения ближайших целей, оказалось, что она жизненно необходима для разрешения многих других вопросов теории чисел. Прежде чем обсуждать гипотезу Римана, нам стоит взглянуть на некоторые теоремы, которые — если бы гипотеза была доказана — из нее следуют.

Одно из важнейших следствий — это величина погрешности в теореме о распределении простых чисел. Теорема, как вы помните, утверждает, что для большого x отношение π(x) к Li(x) приближается к 1, причем чем дальше, тем сильнее. Иными словами, разница между двумя функциями снижается до нуля относительно величины x. Однако реальная разница при этом может расти (и растет). Просто она делает это медленнее, чем растет сам x. Компьютерные расчеты позволяют предположить, что величина погрешности примерно пропорциональна √xlogx. Если гипотеза Римана верна, это утверждение можно доказать. В 1901 г. Хельге фон Кох доказал, что гипотеза Римана логически эквивалентна оценке

для всех x ≥ 2657. Здесь вертикальными линиями обозначена абсолютная величина: разность, умноженная на ±1, чтобы сделать ее положительной. Эта формула дает наилучшие возможные ограничения для разницы между π(x) и Li(x).

Из гипотезы Римана можно получить немало других оценок для функций теории чисел. К примеру, из нее прямо следует, что сумма делителей n меньше

для всех n ≥ 5040, где γ — постоянная Эйлера (γ = 0,57721). Эти утверждения могут показаться случайными и странными фактами, но хорошая оценка для важной функции жизненно важна во многих приложениях, и большинство специалистов по теории чисел отдали бы свою правую руку ради того, чтобы доказать любую из них.

Кроме того, гипотеза Римана говорит нам, насколько велико может быть расстояние между последовательными простыми числами. Типичный размер промежутка между ними можно вывести на основании теоремы о распределении простых чисел: в среднем промежуток между простым числом p и следующим простым числом сравним с log p. Некоторые промежутки могут быть меньше, некоторые больше, но математикам жилось бы легче, если бы можно было сказать наверняка, насколько велики могут быть самые большие из них. Харальд Крамер доказал в 1936 г., что если гипотеза Римана верна, то промежуток при простом числе p не может превышать величины √plog p, домноженной на некую константу.

Но подлинное значение гипотезы Римана куда глубже. Существуют далеко идущие обобщения и сильное подозрение, что тот, кто сумеет доказать гипотезу Римана, сможет, вероятно, доказать и связанную с ней обобщенную гипотезу Римана. А это, в свою очередь, даст математикам власть над обширными областями теории чисел.

Обобщенная гипотеза Римана вырастает из более подробного описания простых чисел. Все простые числа, кроме двойки, нечетные, и в главе 2 мы видели, что все нечетные простые можно разделить на два типа: те, что на 1 больше числа, кратного 4, и те, что на 3 больше числа, кратного 4. Говорят, что это числа вида 4k + 1 или 4k + 3, где k — число, на которое вы умножаете 4, чтобы получить данное простое число. Приведем короткий список первых нескольких простых чисел того и другого типа, вместе с соответствующими числами, кратными 4:

Прочерки указывают на то, что соответствующее число не простое.

Сколько существует простых чисел того и другого типа? Как они распределены среди всех простых чисел или среди всех целых чисел? Евклидово доказательство того факта, что простых чисел существует бесконечно много, можно без больших усилий модифицировать, доказав при этом, что существует бесконечно много простых чисел вида 4k + 3. Доказать, что простых чисел вида 4k + 1 тоже бесконечно много, гораздо сложнее, — это можно сделать, но лишь при помощи некоторых достаточно сложных теорем. Разница в подходах обусловлена тем, что любое число вида 4k + 3 имеет делитель того же вида, а в отношении чисел вида 4k + 1 это не всегда верно.

В числах этих двух видов нет ничего чудесного или священного. Все простые числа, кроме 2 и 3, имеют вид 6k + 1 или 6k + 5, и мы можем задать в отношении них аналогичные вопросы. Если уж на то пошло, все простые числа, кроме 5, имеют вид 5k + 1, 5k + 2, 5k + 3, 5k + 4. Мы оставляем в стороне числа вида 5k, поскольку они кратны 5 и, соответственно, все, кроме 5, не являются простыми.

Кстати говоря, на любой из подобных вопросов нетрудно выдвинуть разумное предположение — простые числа в арифметической последовательности. Случай с 5k достаточно типичен. Эксперимент быстро показывает, что числа приведенных выше четырех видов имеют примерно равные шансы оказаться простыми. Вот похожая таблица:

Так что должно существовать бесконечное количество простых чисел каждого вида, и в среднем к каждому виду должна относиться четверть всех простых чисел до заданного предела.

Для некоторых видов доказать, что простых чисел такого вида существует бесконечно много, совсем несложно. Для других видов требуются более изощренные рассуждения. Но до середины XIX в. никому не удавалось доказать, что существует бесконечно много простых чисел каждого возможного вида, не говоря уже о том, чтобы доказать их более или менее равномерное распределение. Лагранж в 1785 г. в работе, посвященной закону квадратичной взаимности — глубокому свойству квадратов простых модулей, — принимал этот факт без доказательства. Результаты дали очевидно полезные следствия, и пора было кому-нибудь это доказать. В 1837 г. Дирихле выяснил, как применить идеи Эйлера, связанные с теоремой о распределении простых чисел, для доказательства обоих этих утверждений. Первым делом следовало определить аналоги дзета-функции для этих типов простых чисел. То, что получилось, называется L-функциями Дирихле. К примеру, в случае 4k + 1/4k + 3 возникает следующая функция:

где коэффициенты равны +1 для чисел вида 4k + 1, −1 для чисел вида 4k + 3 и 0 для остальных. Греческую букву χ называют характером Дирихле, и это напоминает нам о том, какие именно знаки следует использовать.

Для римановой дзета-функции важен не только ряд, но и его аналитическое продолжение, придающее функции значения во всех комплексных точках. То же относится и к L-функции, и Дирихле определил подходящее аналитическое продолжение. Приспособив к случаю идеи, которые использовались для доказательства теоремы о распределении простых чисел, он сумел доказать аналогичную теорему о простых числах особых видов. К примеру, число простых чисел вида 5k + 1, меньших или равных x, асимптотически приближается к Li(x)/4; то же относится и к остальным трем случаям 5k + 2, 5k + 3, 5k + 4. Это означает, что простых чисел каждого вида бесконечно много.

Риманова дзета-функция — это особый случай L-функции Дирихле для простых чисел вида 1k + 0, т. е. для всех простых чисел. Обобщенная гипотеза Римана представляет собой очевидное обобщение оригинальной гипотезы: нули любой L-функции Дирихле либо имеют действительную часть, равную 1/2, либо являются тривиальными нулями, действительная часть которых отрицательна или больше единицы.

Если обобщенная гипотеза Римана верна, то верна и обычная его гипотеза. Многие следствия обобщенной гипотезы Римана аналогичны следствиям обычной. К примеру, схожие границы ошибки можно доказать для аналогичных версий теоремы о распределении простых чисел в применении к простым числам любого конкретного вида. Однако обобщенная гипотеза Римана подразумевает много такого, что совершенно отличается от всего, что мы можем вывести из обычной гипотезы Римана. Так, в 1917 г. Годфри Харди и Джон Литтлвуд доказали, что из обобщенной гипотезы Римана следует гипотеза Чебышева, в том смысле, что (буквально) простые числа вида 4k + 3 встречаются чаще, чем числа вида 4k + 1. Согласно теореме Дирихле, оба вида равновероятны в конечном итоге, но это не мешает простым числам вида 4k + 3 выигрывать у чисел 4k + 1, конечно, в правильной игре.

У обобщенной гипотезы Римана есть также важные следствия, имеющие отношение к проверке на простоту, такие как тест Миллера 1976 г., упомянутый в главе 2. Если обобщенная гипотеза Римана верна, то тест Миллера дает нам эффективный алгоритм проверки. Оценка эффективности более поздних тестов тоже зависит от обобщенной гипотезы Римана. Существуют и важные приложения для алгебраической теории чисел. Помните, в главе 7 говорилось, что новое определение идеальных чисел Куммера, данное Дедекиндом, привело к рождению новой фундаментальной концепции — понятия идеала. Разложение на простые множители в кольцах алгебраических целых чисел существует, но может не быть единственным. Разложение идеалов на простые множители работает много лучше: и существование, и единственность гарантированы. Так что имеет смысл заново рассмотреть все вопросы о множителях в терминах идеалов. В частности, существует понятие «простого идеала» — разумной и удобной аналогии простого числа.

Зная это, естественно спросить, есть ли у эйлеровой связи между обычными простыми числами и дзета-функцией аналог для простых идеалов. Если да, то весь мощный аппарат аналитической теории чисел применим к алгебраическим числам. Оказывается, это можно сделать, с глубокими и очень серьезными последствиями. Результат — дзета-функция Дедекинда — по одной такой функции на каждую систему алгебраических чисел. Существует глубокая связь между комплексными аналитическими свойствами дедекиндовой дзета-функции и арифметикой простых чисел в соответствующей системе алгебраических целых чисел. И, разумеется, существует аналог гипотезы Римана: все нетривиальные нули дедекиндовой дзета-функции лежат на критической линии. Понятие «обобщенная гипотеза Римана» теперь включает в себя и это утверждение.

Даже генерализация — еще не конец истории дзета-функции. Она вдохновила ученых на определение аналогичных функций в нескольких других областях математики — от абстрактной алгебры до теории динамических систем. Во всех этих областях существуют еще более масштабные аналоги гипотезы Римана. Некоторые из них даже доказаны. В 1974 г. Пьер Делинь доказал такой аналог для многообразий над конечными полями. Обобщения, известные как дзета-функции Сельберга, тоже удовлетворяют аналогу гипотезы Римана. То же можно сказать о дзета-функции Госса. Однако существуют другие обобщения — дзета-функции Эпштейна, для которых аналог гипотезы Римана неверен. Здесь бесконечное множество нетривиальных нулей лежит на критической линии, но некоторые — нет, что продемонстрировал Эдвард Титчмарш. С другой стороны, эти дзета-функции не имеют эйлеровой формулы в виде произведения и потому не похожи на римановы дзета-функции в аспекте, который вполне может оказаться принципиально важным.

Имеется множество косвенных свидетельств того, что гипотеза Римана — как оригинальная, так и обобщенная — справедлива. Много хорошего следовало бы из истинности этих гипотез. Ни одно из этих следствий за все время не удалось опровергнуть, а ведь сделать это — то же самое, что опровергнуть гипотезу Римана. Но ни доказательства, ни опровержения пока нет. Широко распространено мнение, что доказательство оригинальной гипотезы Римана открыло бы дорогу и к доказательству обобщенного ее варианта. Но на самом деле, возможно, лучше было бы атаковать сразу обобщенную гипотезу Римана во всей ее грозной красе — воспользоваться всем арсеналом доступных на сегодняшний день методов, доказать, а затем вывести оригинальную гипотезу Римана как ее частный случай.

В пользу гипотезы Римана имеется также огромное количество экспериментальных данных — по крайней мере огромное на первый взгляд, пока кто-нибудь не плеснет холодной воды, чтобы остудить горячие головы. По данным Карла Людвига Зигеля, Риман вычислил несколько первых нулей своей дзета-функции, но не стал публиковать результат. Они находятся в точках

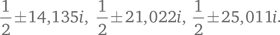
Нетривиальные нули всегда располагаются парами, как здесь. Я написал в них, а не 0,5, потому что действительная часть в этих случаях известна точно, выяснена при помощи общих результатов комплексного анализа и известных свойств дзета-функции. То же можно сказать и о компьютерных расчетах, о которых речь пойдет ниже. Они не просто показывают, что нули находятся очень близко к критической линии; они действительно находятся на ней.

В 1903 г. Йорген Грам продемонстрировал численно, что первые десять нулей (т. е. ±-пар) лежат на критической линии. К 1935 г. Титчмарш увеличил число таких нулей до 195. В 1936 г. Титчмарш и Лесли Комри доказали, что первая 1041 пара нулей лежит на критической линии. Это был последний раз, когда подобные расчеты проводились вручную.

Алан Тьюринг больше всего известен тем, что во время войны работал в Блетчли-парке, где участвовал в разгадывании германского кода «Энигма», а также своими работами, заложившими фундамент компьютерных вычислений и искусственного интеллекта. Но, помимо всего этого, Тьюринг интересовался и аналитической теорией чисел. В 1953 г. он открыл более эффективный способ вычисления нулей дзета-функции и определил при помощи компьютера, что первые 1104 пары нулей лежат на критической линии. Свидетельства того, что все нули до некоторого предела лежат на критической линии, множились и множились. Нынешний рекорд, полученный Янником Саутером и Патриком Демишелем в 2004 г., составляет 10 трлн (10¹³). Тем временем математики и компьютерщики проверяли другие диапазоны нулей. На сегодня все без исключения нетривиальные нули, когда-либо кем-либо рассчитанные, лежат на критической линии.

Все это может показаться исчерпывающим доказательством, но математики не спешат принимать его на веру, и не без причины. Может показаться, что 10 трлн — это очень много, но в теории чисел часто значение имеет не само число, а его логарифм, а он пропорционален числу знаков в числе. Натуральный логарифм от 10 трлн чуть меньше 30. Мало того, во многих задачах фигурирует логарифм от логарифма или даже логарифм от логарифма от логарифма. В этих терминах 10 трлн — это крохотная величина, так что численное доказательство до 10 трлн включительно почти ничего не значит.

Существуют и кое-какие обобщенные аналитические доказательства, к которым эта критика не относится. Харди и Литтлвуд доказали, что на критической линии лежит бесконечное число нулей. Другие математики показали в точном смысле, что почти все нули лежат очень близко к критической линии. Сельберг доказал, что ненулевая доля нулей лежит непосредственно на критической линии. Норманн Левинсон доказал, что эта доля — по крайней мере треть и теперь она увеличена по крайней мере до 40 %. Все эти результаты позволяют предположить, что если гипотеза Римана неверна, то нули, не лежащие на критической линии, очень велики и встречаются очень редко. К несчастью, главное следствие из всего этого заключается в том, что если такие исключения существуют, то найти их будет необычайно трудно.

Но зачем волноваться? Ведь численных свидетельств должно быть достаточно, чтобы убедить любого разумного человека? К несчастью, нет. Численные свидетельства не убеждают математиков, и в данном случае это не просто педантизм и придирки: они действуют разумно. В математике в целом, а особенно в теории чисел, обширные, на первый взгляд, «экспериментальные» данные часто имеют гораздо меньший вес, чем может показаться.

Наглядным примером служит гипотеза Пойа, которую в 1919 г. выдвинул венгерский математик Дьердь Пойа. Он предположил, что по крайней мере половина всех целых чисел вплоть до заданной величины имеет нечетное число простых множителей. Повторяющиеся множители в данном случае учитываются отдельно, а начинаем мы с 2. К примеру, число простых множителей для предела 20 приведено в табл. 2, где последняя колонка отражает процент чисел до данного предела с нечетным числом простых множителей.

Все значения в последней колонке выше 50 %, а более обширные расчеты позволяют предположить, что это всегда так. В 1919 г., без всяких компьютеров, исследователи не смогли найти чисел, которые опровергли бы эту гипотезу. Но в 1958 г. Брайан Хазелгроув доказал при помощи аналитической теории чисел, что гипотеза Пойа неверна для некоего числа — числа, не превосходящего 1,845 × 10³⁶¹, если быть точным. Как только на сцене появились компьютеры, Шерман Леман показал, что гипотеза неверна для 906 180 359. К 1980 г. Минору Танака доказал, что минимальное из таких чисел 906 150 257. Так что вы могли бы собрать экспериментальные данные по всем числам почти до миллиарда и не понять, что гипотеза неверна.

Тем не менее приятно знать, что число 906 150 257 необычайно интересно.

Разумеется, сегодняшние компьютеры, если их как следует запрограммировать, опровергли бы гипотезу Пойа в несколько секунд. Но иногда не помогают даже они. Классический пример — число Скьюза, где первоначально громадное количество численных данных указывало на то, что некая знаменитая гипотеза верна, но на самом деле она неверна. Это гигантское число появилось в задаче, тесно связанной с гипотезой Римана: аппроксимацией π(x) функции Li(x). Как мы только что видели, теорема о распределении простых чисел утверждает, что, когда x становится большим, отношение этих двух величин стремится к 1. Численные расчеты указывают на более сильное утверждение: это отношение всегда меньше 1, т. е. π(x) меньше Li(x). В 2008 г. численные расчеты Тадея Котника показали, что это верно для x меньше 10¹⁴. К 2012 г. Дуглас Столл и Демишель повысили этот предел до 10¹⁸, и такой же результат независимо от них получил Андрей Кульша. А расчеты Томаша Оливейра-и-Сильва позволяют предположить, что предел может быть увеличен до 10²⁰.

Таблица 2. Процент чисел до заданного предела, имеющих нечетное число простых множителей

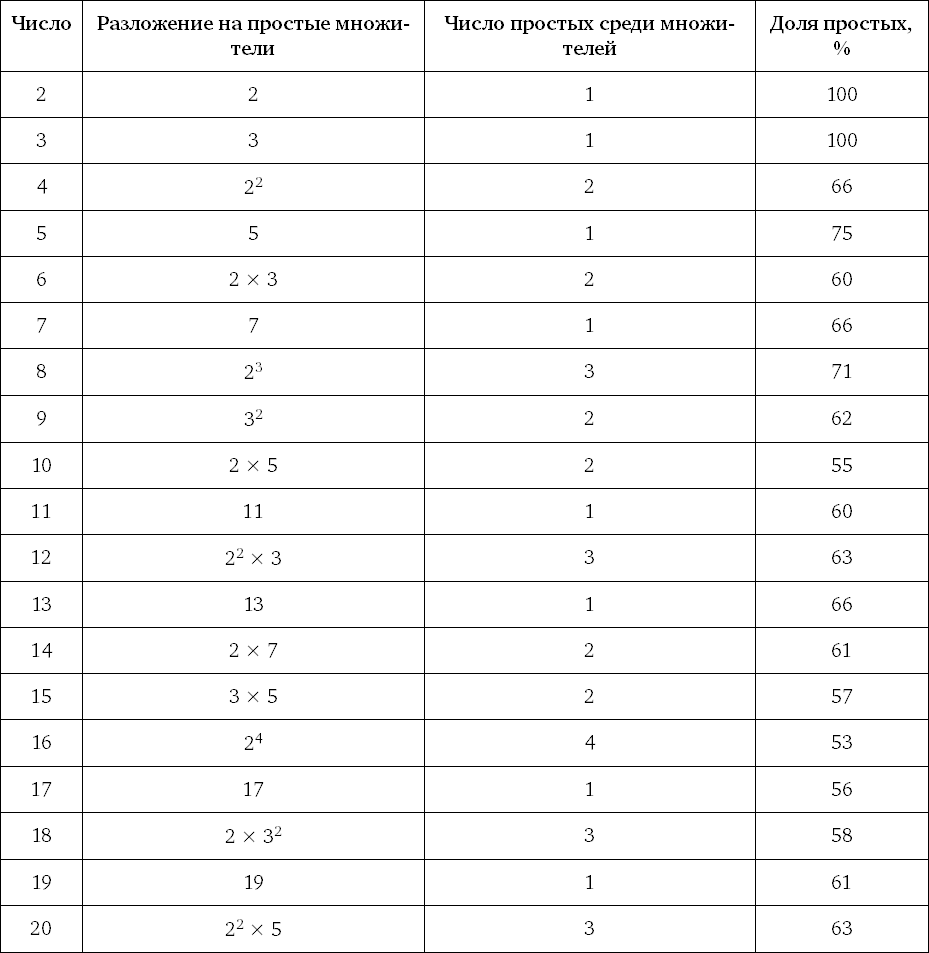
Звучит, кажется, исчерпывающе. Данные здесь сильнее, чем лучшие численные результаты, полученные до сих пор для гипотезы Римана. Но в 1914 г. Литтлвуд доказал, что эта гипотеза неверна — и как доказал! По мере того как x проходит через положительные действительные значения, разность π(x) — Li(x) меняет знак (с отрицательного на положительный или наоборот) бесконечно часто. В частности, π(x) больше Li(x) для некоторых достаточно больших значений x. Однако доказательство Литтлвуда ничего не говорило о конкретных значениях x.

В 1933 г. его ученик, южноафриканский математик Стенли Скьюз, оценил, насколько большим должен быть x: не более 10∧10∧10∧34, где знак ∧ обозначает «возвести в степень». Это настолько гигантское число, что если все его цифры напечатать в книге — довольно скучной книге, состоящей из 1 с бесконечными нулями, — то Вселенная не вместила бы этой книги, даже если бы каждая цифра была размером с элементарную частицу. Более того, чтобы доказательство работало, Скьюзу пришлось принять на веру истинность гипотезы Римана. К 1955 г. он нашел способ обойтись без гипотезы Римана, но не бесплатно: его оценка увеличилась до 10∧10∧10∧963.

Эти числа слишком велики даже для прилагательного «астрономический», но дальнейшие исследования помогли снизить их до величин, которые уже можно охарактеризовать как космологические. В 1966 г. Леман заменил числа Скьюза на 10¹¹⁶⁵. Те Риеле в 1987 г. понизил эту оценку до 7 × 10³⁷⁰, а в 2000 г. Картер Бейз и Ричард Хадсон свели ее к 1,39822 × 10³¹⁶. Затем Чжоу Куок Фай и Роджер Плаймен срезали еще немножко и довели ограничение до 1,39801 × 10316. Это изменение может показаться несущественным, но на самом деле данная оценка меньше предыдущей на 2 × 10³¹². А Саутер и Демишель еще улучшили этот результат, сведя его к 1,3971667 × 10³¹⁶.

Но пока суд да дело, в 1941 г. Аурел Уинтнер доказал, что маленькая, но ненулевая доля целых чисел удовлетворяет неравенству π(x) > Li(x). В 2011 г. Столл и Демишель просчитали первые 200 млрд нулей дзета-функции, что позволяет судить о π(x) для всех x вплоть до ^{1010 000 000 000 000}, и нашли доказательство того, что если x меньше, чем 3,17 × 10¹¹⁴, то π(x) меньше Li(x). Так что для данной конкретной проблемы все свидетельства по крайней мере до 10¹⁸, а очень может быть, что и до 10¹¹⁴ или даже больше, только вводят в заблуждение. Переменчивые боги теории чисел любят пошутить за счет людей.

Было предпринято немало попыток доказать или опровергнуть гипотезу Римана. На сайте Мэттью Уоткинса «Предлагавшиеся доказательства гипотезы Римана» перечислены около 50 таких попыток, сделанных уже после 2000 г. Во многих доказательствах найдены ошибки, и ни одно из них профессиональное сообщество не признало верным.

Одной из самых разрекламированных в последние годы стала попытка Луи де Бранжа, предпринятая в 2002 г. Он распространил среди математиков рукопись, в которой попытался доказать гипотезу Римана при помощи области анализа, имеющей дело с преобразованиями на пространствах бесконечной размерности и известной как функциональный анализ. У специалистов были основания принять попытку де Бранжа всерьез. Незадолго до того он так же распространил доказательство гипотезы Бибербаха о разложении в ряд комплексных функций. В первоначальном доказательстве обнаружились ошибки, но со временем было установлено, что основная его идея работает. Однако в данном случае казалось, что предложенный де Бранжем метод доказательства гипотезы Римана не имеет шансов на успех. Брайан Конри и Ли Сяньцзинь указали на некоторые непреодолимые, как пока представляется, препятствия.

Возможно, самая серьезная надежда на доказательство гипотезы Римана заключается в новых методах или радикально новых подходах к задаче. Как мы неоднократно видели, прорывы в работе по великим математическим задачам происходят, как правило, тогда, когда кому-нибудь удается связать давно известную задачу с совершенно другой, далекой от нее областью математики. Прекрасный пример — Великая теорема Ферма: как только ее удалось интерпретировать как вопрос об эллиптических кривых, прогресс не заставил себя ждать.

Сегодня тактика де Бранжа вызывает вопросы, но сам его подход стратегически вполне оправдан. Своими корнями он уходит в устное предположение, сделанное около 1912 г. Давидом Гильбертом и независимо от него Дьердем Пойа. Эдмунд Ландау тогда спросил у Пойа, по каким таким физическим причинам должна быть верна гипотеза Римана. В 1982 г. Пойа вспоминал, что нашел-таки тогда ответ: нули дзета-функции следует связать с собственными значениями так называемого самосопряженного оператора. Речь идет о характеристических числах, связанных с особым типом преобразования. В квантовой физике — одной из важнейших областей применения — эти числа определяют энергетические уровни системы, и существует стандартная несложная теорема о том, что собственные числа этого особого типа преобразования всегда действительны. Если бы собственные числа некоего самосопряженного оператора совпадали с нулями кси-функции, то гипотеза Римана была бы несложным следствием этого факта. Пойа не стал публиковать эту идею — он не мог привести пример такого оператора, а пока примера нет — все это журавль в небе. Но в 1950 г. Сельберг доказал свою «формулу следа», которая связывает геометрию поверхности с собственными числами соответствующего оператора. Это сделало идею чуть более правдоподобной.

В 1972 г. Хью Монтгомери побывал в Институте перспективных исследований в Принстоне. В разговоре с физиком Фрименом Дайсоном он упомянул замеченные им некоторое время назад удивительные статистические свойства нетривиальных нулей дзета-функции. Дайсон сразу же отметил их сходство со статистическими свойствами случайных эрмитовых матриц — еще одного частного случая оператора, который используется для описания квантовых систем, таких как атомное ядро. В 1999 г. Ален Конн предложил формулу следа, аналогичную формуле Сельберга. Подтвердить ее — означало бы доказать обобщенную гипотезу Римана. В том же 1999 г. физики Майкл Берри и Йон Китинг предположили, что требуемый оператор может быть получен при квантовании одного хорошо известного понятия из классической физики, имеющего отношение к импульсу. Получившуюся в результате гипотезу Берри можно рассматривать как частную версию гипотезы Гильберта — Пойа.

Эти идеи, помогающие соотнести гипотезу Римана с глубинными областями математической физики, очень интересны. Они показывают, что решение может прийти из, казалось бы, никак не связанных с ней областей математики, и внушают надежду на то, что когда-нибудь вопрос с гипотезой Римана будет закрыт. Однако до сих пор они не привели к окончательному прорыву, и у нас нет оснований считать, что решение уже близко. Гипотеза Римана остается одной из самых запутанных и волнующих загадок во всей математике.

Сегодня у исследователей появился новый стимул к борьбе за доказательство гипотезы Римана: крупный приз.

В математике не существует Нобелевской премии. Самой престижной наградой в этой области является Филдсовская премия за выдающиеся открытия, вместе с которой вручается медаль. Эта премия названа в честь канадского математика Джона Филдса, который и завещал на нее средства. Раз в четыре года на Международном конгрессе математиков двум, трем или четырем молодым ученым не старше 40 лет вручают золотую медаль и денежную премию (в настоящее время это $15 000).

Многие представители математической науки считают правильным, что в их области не присуждается Нобелевская премия. В настоящее время она составляет чуть больше миллиона долларов, а такая сумма легко может исказить цели исследователей и породить споры о приоритетах. Однако отсутствие крупной математической премии также может исказить представления общества о значимости и полезности этой науки. Можно подумать, что открытия, за которые никто не хочет платить, не так уж важны. Возможно, поэтому не так давно появились две очень престижные новые математические премии. Одна из них — Абелевская — присуждается ежегодно Норвежской академией науки и словесности и названа в честь великого норвежского математика Нильса Хенрика Абеля. Вторая награда — это премии за решение семи «проблем тысячелетия», объявленные Математическим институтом Клэя. Этот институт основали в 1998 г. в Кембридже (штат Массачусетс) американский бизнесмен Лэндон Клэй и его жена Лавиния. Лэндон Клэй активно занимается паевыми инвестиционными фондами и при этом любит и уважает математику. Его организация проводит встречи, выделяет гранты на исследования, организует публичные лекции и присуждает ежегодную премию за математические исследования.

В 2000 г. сэр Майкл Атья и Джон Тейт, ведущие математики Великобритании и США, объявили, что Математический институт Клэя учредил новую премию, которая должна будет стимулировать работу над семью важнейшими нерешенными задачами математики. Эти задачи будут известны как «проблемы тысячелетия», а надлежащим образом опубликованное и отреферированное решение любой из них будет вознаграждено денежной суммой в $1 млн. Все вместе эти задачи призваны привлечь внимание к некоторым центральным для математики вопросам, до сих пор не имеющим ответов. Вопросы эти были тщательно отобраны лучшими математиками мира. Немалый приз должен ясно показать обществу: математика имеет огромную ценность. Всякий, кто имеет отношение к науке, прекрасно знает, что интеллектуальная ценность вполне может быть выше любых денег, но все же деньги помогают сосредоточиться. Самой известной и давней из задач тысячелетия является гипотеза Римана. Это единственный вопрос, который вошел одновременно и в список Гильберта (1900), и в список задач тысячелетия. Остальные шесть проблем тысячелетия обсуждаются далее в главах 10–15. Тем не менее математики не особенно гонятся за призами, и работа над гипотезой Римана продолжалась бы и без обещанной премии. Все, что для этого нужно, — новая перспективная идея.

Стоит также помнить о том, что гипотезы, даже освященные временем, иногда оказываются ошибочными. Сегодня большинство математиков, судя по всему, считает, что когда-нибудь гипотеза Римана будет доказана. Некоторые, однако, думают, что она, возможно, все-таки неверна, и где-то в дебрях очень больших чисел может скрываться нуль дзета-функции, который не лежит на критической линии. Если такой «контрпример» существует, то он, скорее всего, окажется очень-очень большим.

Однако на переднем крае математики просто мнение стоит немного. Интуиция зачастую очень помогает ученым, но известно немало случаев, когда это замечательное чувство ошибалось. Житейский здравый смысл может лгать, оставаясь при этом и общепризнанным, и здравым. Литтлвуд, один из лучших знатоков комплексного анализа, выразился вполне однозначно: в 1962 г. он сказал, что уверен в ошибочности гипотезы Римана, и добавил, что нет никаких мыслимых причин, по которым она была бы верна. Кто прав? Поживем, увидим.