10. Какой формы сфера? Гипотеза Пуанкаре

Анри Пуанкаре был одним из величайших математиков конца XIX в., слегка эксцентричным, но исключительно прозорливым ученым. Он был членом французского Бюро долгот — организации, созданной для решения астрономических задач для целей навигации, слежения за временем и измерения Земли и других планет. Членство в ней привело Пуанкаре к мысли об установлении международной системы временны`х зон. Кроме того, оно вдохновило ученого на размышления о времени и, в частности, на предвосхищение некоторых открытий Эйнштейна в области теории относительности. Вклад Пуанкаре виден в математике всюду, от теории чисел до математической физики. В частности, он был одним из основателей топологии, математики непрерывных преобразований.

В 1904 г. Пуанкаре наткнулся на простой, казалось бы, вопрос и вдруг понял, что ответ на него, который он прежде использовал в работе как нечто очевидное, доказать не в состоянии. «Этот вопрос увел бы нас далеко в сторону», — написал он, погрешив против истины: на самом деле, этот вопрос упрямо отказывался вести его куда бы то ни было. Хотя сам Пуанкаре сформулировал задачу в виде вопроса, известность она приобрела как гипотеза Пуанкаре — все были уверены в том, что ответом на вопрос должно быть «да». Это еще одна из семи «проблем тысячелетия» по версии Института Клэя, что вполне справедливо, поскольку несложная на вид задача оказалась одной из самых сложных во всей топологии. Ответ на вопрос Пуанкаре дал в 2002 г. молодой русский математик Григорий Перельман. Его решение привнесло в науку массу новых идей и методов — так много, что математическому сообществу потребовалось несколько лет, чтобы «переварить» представленное доказательство и признать его верным.

За свое достижение Перельман был удостоен самой престижной в математике Филдсовской премии, но отказался от нее. Он избегает всякой публичности. Ему предложили миллион долларов — премию Института Клэя, — но и ее Перельман не принял. Деньги ему тоже не нужны. Он хотел лишь, чтобы его труд был принят математическим сообществом. Со временем так и произошло, но, к несчастью, процесс занял немало времени. Да и вообще, наивно было ожидать признания без публичности и премий. Но склонная к затворничеству натура Перельмана не смогла принять эти неизбежные следствия успеха.

Мы уже встречались с топологией в связи с теоремой о четырех красках, и я прибегал тогда к расхожему сравнению: «геометрия на резиновом листе». Евклидова геометрия имеет дело с прямыми линиями, окружностями, длинами и углами. Она разворачивается на плоскости или в пространстве трех измерений, где становится более сложной. Плоскость похожа на бесконечный лист бумаги, и у нее с бумагой есть одна общая черта: она не растягивается, не сжимается и не сгибается. Бумагу можно скатать в трубочку, и она может слегка съежиться или растянуться — особенно если пролить на нее кофе. Но невозможно обернуть бумагой шар так, чтобы на листе не образовалось складок. Математически евклидова плоскость — штука жесткая. В геометрии Евклида две фигуры — два треугольника, квадрата или круга — равны, если один из них получен из другого посредством жесткого перемещения. А «жесткость» перемещения означает, что расстояния при этом не меняются.

Но что если использовать вместо бумаги эластичный резиновый лист? Он, в отличие от бумаги, растягивается и сгибается, при некотором желании его можно даже сжать. Длины и углы на эластичном листе не имеют фиксированных значений. Более того, если лист достаточно эластичен, треугольников, квадратов и кругов на нем тоже нет. Можно деформировать треугольник на резиновом листе так, что у него появится дополнительный угол. Можно даже превратить его в круг (см. рис. 36). Какими бы понятиями ни оперировала геометрия на резиновом листе, ясно, что традиционным евклидовым концепциям в ней места нет.

Может показаться, что «геометрия на резиновом листе» будет настолько гибкой, что в ней вообще не найдется места для сколько-нибудь постоянных смыслов, а значит, и доказать ничего невозможно. Но это не так. Нарисуйте, к примеру, треугольник и поставьте внутри него точку. Если вы начнете растягивать и деформировать лист, превращая треугольник в круг, то одно свойство вашего чертежа все же сохранится: точка останется внутри. Согласен, теперь она находится внутри круга, а не треугольника, но это не важно: она же все равно не снаружи. Чтобы переместить точку наружу, вам придется разорвать лист, а это будет означать нарушение правил игры.

И еще одно свойство не изменяется при искажении. Треугольник — это простая замкнутая кривая. Это линия, замкнутая сама на себя, без свободных концов и самопересечений. Восьмерка — тоже замкнутая кривая, но уже не простая — у нее есть самопересечение. При деформировании резинового листа треугольник может изменить форму, но обязательно останется простой замкнутой кривой. Невозможно, к примеру, превратить его в восьмерку, не разорвав листа.

В трехмерной топологии все пространство становится эластичным. Не так, как куб из резины, который, если снять давление, возвращается к первоначальной форме, а как гель, форму которого можно менять без всякого сопротивления. Топологическое пространство бесконечно эластично: можно взять участок размером с рисовое зернышко и раздуть его до размеров Солнца. Можно тянуть из него щупальца, пока он не начнет напоминать формой осьминога. Единственное, чего делать не разрешается, — это каким бы то ни было образом нарушать непрерывность. Не следует допускать разрывов пространства и вообще проделывать любые операции, способные разделить соседние точки.

Какие свойства пространственных фигур сохраняются при всех непрерывных деформациях? Не длина, не площадь, не объем… А вот заузленность сохраняется. Если завязать кривую узлом и соединить концы, создав замкнутую петлю, то узел уже никуда не денется. Как бы вы ни деформировали пространство, кривая останется завязанной. Таким образом, мы имеем дело с геометрией нового типа, где важные и осмысленные концепции кажутся, на первый взгляд, несколько расплывчатыми: «внутри», «замкнутый», «простой», «завязанный». Называется эта новая геометрия весьма респектабельно: топологией. Нематематику она может показаться странной или даже абсурдной, но на поверку это одна из основных областей математики ХХ в., и свое значение она сохраняет и в XXI в. А Пуанкаре — один из тех, кого мы в первую очередь должны за это благодарить.

История топологии началась почти за столетие до Пуанкаре — в 1813 г. Симон Люилье, швейцарский математик, при жизни не снискал громкой славы, но отверг крупную сумму денег, которую кто-то из его родственников предлагал ему за принятие церковного сана. Люилье предпочел карьеру в математике. Работал он в основном в тихой математической заводи: занимался теоремой Эйлера о многогранниках. В главе 4 мы упоминали один занятный и вроде бы ни с чем не связанный факт: если у многогранника F граней, V вершин и E ребер, то F — E + V = 2. Люилье большую часть жизни исследовал варианты этой формулы, и с высоты сегодняшнего дня ясно, что он сделал важнейший шаг в направлении топологии, когда обнаружил, что формула Эйлера не всегда верна. Ее применимость зависит от качественных характеристик многогранника.

Формула верна для многогранников без отверстий, которые можно нарисовать на поверхности сферы или на поверхности, полученной из сферы непрерывным преобразованием. Но если в многограннике есть отверстия, формула перестает работать. К примеру, рамка для картины, изготовленная из прямоугольного в сечении деревянного бруска имеет 16 граней, 32 ребра и 16 вершин; здесь F — E + V = 0. Люилье доработал формулу Эйлера для подобных экзотических многогранников: если в многограннике g отверстий, то F — E + V = 2 − 2g. Так был открыт первый важный топологический инвариант: величина, которая связана с пространством и не меняется при любых непрерывных преобразованиях пространства. Инвариант Люилье позволяет точно подсчитать, сколько отверстий имеет та или иная поверхность, не определяя строго, что такое «отверстие». Это полезно, поскольку «отверстие» — понятие достаточно сложное. Отверстие — не часть поверхности и не область вне поверхности. Очевидно, это свойство того, как поверхность располагается в окружающем пространстве. Но открытие Люилье показывает, что то, что мы интерпретируем как количество отверстий, есть свойство, изначально присущее поверхности и не зависящее от окружающего пространства. Нет необходимости определять отверстия, а затем считать их; лучше вообще не делать этого.

После Люилье следующей ключевой фигурой в предыстории топологии стал Гаусс. Работая в различных областях математики, он столкнулся с несколькими другими топологическими инвариантами. Работа в комплексном анализе, особенно над доказательством того, что каждое полиномиальное уравнение имеет по крайней мере одно решение в комплексных числах, заставила его рассмотреть порядок кривой на плоскости: сколько оборотов она делает относительно заданной точки. Задачи из области электричества и магнетизма подсказали коэффициент зацепления двух замкнутых кривых: сколько раз одна из них проходит сквозь другую. Эти и другие примеры привели Гаусса к мысли о существовании некоего пока не открытого раздела математики, в котором предлагался бы последовательный взгляд на качественные свойства геометрических фигур. Он ничего не публиковал по этой теме, но упоминал ее в письмах и рукописях.

Кроме того, он сообщил эти соображения своему ученику Иоганну Листингу и своему сотруднику Августу Мёбиусу. Я уже упоминал ленту Мёбиуса — поверхность, у которой есть лишь одна сторона и один край. Статью о ней он опубликовал в 1865 г., а саму ее можно увидеть на рис. 9 в главе 4. Мёбиус указал, что определение «имеющая одну сторону» интуитивно понятно, но тем не менее не точно, и предложил вместо него близкое свойство, которое можно определить совершенно строго. Это свойство — ориентируемость. Поверхность ориентируема, если ее можно покрыть сетью треугольников со стрелками вдоль сторон таким образом, что всюду, где два треугольника имеют общую сторону, стрелки указывают в противоположных направлениях. Если вы разместите такую сеть на плоскости и направите все стрелки в треугольниках, к примеру, по часовой стрелке, то именно так и произойдет. А вот на ленте Мёбиуса такая сеть невозможна.

Первая публикация Листинга по топологии появилась раньше, в 1847 г. Называлась она «Лекции по топологии», и это был первый текст, в котором использовалось это слово. Неформально Листинг пользовался им уже около 10 лет. Кроме того, тогда для той же цели использовалась латинская фраза analysis situs, т. е. «анализ размещения», но со временем она вышла из употребления. Книга Листинга не содержит ничего особенно значительного, но дает одно фундаментальное понятие: покрытие поверхности сетью треугольников. В 1861 г., за четыре года до Мёбиуса, Листинг описал ленту Мёбиуса и исследовал связность — вопрос о том, можно ли разбить пространство на две или более несвязанных областей. На основе работы Листинга другие математики, в том числе Вальтер фон Дик, провели полную топологическую классификацию поверхностей, считая их замкнутыми (не имеющими краев) и компактными (конечной протяженности). Оказалось, что любая ориентируемая поверхность топологически эквивалентна сфере с конечным числом g ручек (см. рис. 11 в середине и справа, глава 4). Число g называют родом поверхности, и именно его определяет инвариант Люилье. Если g = 0, это сфера, а если g > 0, мы имеем тор с g отверстиями. Аналогичный ряд поверхностей, начиная с простейшей неориентируемой поверхности — проективной плоскости, — образуют и неориентируемые поверхности. Этот метод был расширен и на поверхности с краями. Каждый край — это замкнутая петля, и единственное, что нужно знать дополнительно, это количество таких петель.

Гипотезу Пуанкаре легче понять, если рассмотреть для начала один из базовых методов, используемых при классификации поверхностей. Ранее я сравнил топологию с деформированием объекта, изготовленного из резины или геля, и подчеркнул, что преобразование обязательно должно быть непрерывным. По иронии судьбы, один из центральных методов топологии включает операцию, которая, на первый взгляд, нарушает непрерывность: разрезание объекта на кусочки. Однако непрерывность восстанавливается при помощи серии правил, описывающих, какие куски соединены друг с другом и как именно. Примером может служить то, как мы определили тор, отождествив противоположные стороны квадрата (см. рис. 12, глава 4).

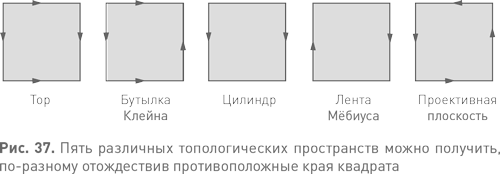
Отождествление четко различимых точек позволяет нам представлять сложные топологические пространства при помощи простых составляющих. Квадрат — это всего лишь квадрат, и ничего больше, но с правилами отождествления квадрат может быть тором, бутылкой Клейна, цилиндром, лентой Мёбиуса или проективной плоскостью, в зависимости от характера правил (см. рис. 37). Так что когда я, объясняя непрерывное преобразование, сравнил его с растягиванием и сгибанием резинового листа, я, строго говоря, требовал больше необходимого. Нам разрешено также разрезать лист на промежуточной стадии при условии, что, в конце концов, мы либо соединим куски в точности так же, как было вначале, либо обозначим правила, которые позволят это сделать. С точки зрения тополога, сформулировать правило склеивания краев — это то же самое, что склеить их. Если, конечно, не забывать это правило в ходе дальнейших операций.

Классический метод классификации поверхностей начинается с рисования на поверхности сети треугольников. Затем мы делаем достаточно много разрезов вдоль сторон треугольника так, чтобы фигура развернулась в плоский многоугольник. Правила склеивания, определяемые тем, как мы делаем разрезы, подскажут нам, как отождествить разные края многоугольника, восстанавливая первоначальную поверхность. В этот момент вся интересующая нас топология заключена в правилах склеивания. Эта классификация доказывается алгебраической обработкой правил и превращением их в правила, определяющие тор с g отверстиями или одну из аналогичных ему неориентируемых поверхностей. У современной топологии есть и другие способы добиться того же самого, но и она часто пользуется техникой «разрезания и склеивания». Этот метод легко обобщается на пространства любой размерности, но он слишком ограничен, чтобы дать возможность классифицировать многоразмерные топологические пространства без дополнительной помощи.

Около 1900 г. Пуанкаре занимался тем, что развивал более раннюю свою работу по топологии поверхностей и разрабатывал значительно более общую методику, применимую к пространствам с любым числом измерений. Основной идеей его исследования был поиск топологических инвариантов: чисел или алгебраических формул, связанных с пространствами, которые при непрерывной деформации остаются неизменными. Если топологические инварианты двух пространств различны, то одно из них невозможно преобразовать в другое и, значит, они топологически различны.

Начал он с обобщения топологического инварианта Люилье F — E + V на многомерные пространства, сделанного итальянским математиком Энрико Бетти в 1870 г. Сейчас оно, отчасти несправедливо, известно как эйлерова характеристика. Бетти заметил, что наибольшее число замкнутых кривых, которые можно нарисовать на поверхности рода g, не поделив ее при этом на несвязные куски, равняется g − 1. Это еще один способ топологически охарактеризовать поверхность. Бетти обобщил эту идею на «числа связности» любой размерности, которые Пуанкаре назвал числами Бетти, и этот термин используется до сих пор. Так, k-мерное число Бетти означает число k-мерных отверстий в пространстве.

Пуанкаре определил на основе чисел Бетти более чувствительный инвариант, получивший название гомологии. Для него характерна гораздо более четкая алгебраическая структура. Подробнее мы поговорим о гомологии в главе 15. Пока же достаточно сказать, что гомология анализирует наборы многомерных «граней» в подобной сети и задается вопросом о том, какие из них образуют границу топологического диска. Диск не имеет отверстий, в отличие от тора, так что мы можем быть уверены, что в пределах любого набора граней, образующего границу, отверстий нет. Напротив, мы можем обнаруживать отверстия путем разделения наборов граней на те, что образуют границу, и на те, что границы не образуют. Таким образом мы можем построить серию инвариантов пространства, известных как его гомологические группы. Слово «группа» здесь используется как термин из абстрактной алгебры, означающий, что из любых двух объектов группы при помощи операции, для которой выполняются несколько соответствующих алгебраических правил, может быть получен объект той же группы. Позже, когда нам потребуется это понятие, я расскажу о нем немного больше. Для каждого измерения от 0 до n существует одна такая группа, и для каждого пространства мы получаем серию топологических инвариантов со всевозможными интереснейшими алгебраическими свойствами.

Листинг классифицировал все топологические поверхности — пространства размерности 2. Очевидным следующим шагом было посмотреть на пространства размерности 3. И простейшим пространством для начала стала сфера, т. е. бесконечно тонкая поверхность шара. Внутренняя часть шара не считается частью сферы: это всего лишь особенность, возникающая вследствие вложения сферической поверхности в пространство. По существу, у нас есть только поверхность, топологически эквивалентная поверхности шара. Можно представить ее себе как пустотелый мяч с бесконечно тонкой оболочкой.

«Правильный» трехмерный аналог сферы, называемой трехмерной, — это не шар. Шар, конечно, трехмерен, но у него есть граница — его поверхность, сфера. Сама сфера границы не имеет, не должен иметь ее и трехмерный ее аналог. Простейший способ определить трехмерную сферу состоит в том, чтобы в точности воспроизвести координатную геометрию обычной сферы. При этом возникает пространство, которое довольно трудно зрительно представить: я не могу показать вам модель в трех измерениях, поскольку трехмерная сфера хотя и имеет всего три измерения, не вкладывается в обычное трехмерное пространство. Для нее необходимо четырехмерное пространство.

Традиционная единичная сфера в трехмерном пространстве включает в себя все точки, расположенные на расстоянии 1 от заданной точки — центра сферы. Аналогично, единичная трехмерная сфера в четырехмерном пространстве включает в себя все точки, расположенные на единичном расстоянии от ее центра. В системе координат мы можем записать формулу для этих точек, воспользовавшись для определения расстояния обобщением теоремы Пифагора. В более общем случае трехмерная сфера представляет собой любое пространство, топологически эквивалентное единичной трехмерной сфере, в точности так же, как всевозможные выпуклые версии единичной двумерной сферы топологически являются двумерными сферами. Разумеется, то же относится и к более высоким размерностям.

Если этого вам недостаточно и нужен более геометрический образ, попробуйте вот что: трехмерную сферу можно представить как заполненный шар, вся поверхность которого отождествляется с точкой. Это еще один пример применения правила склеивания. В данном случае процесс аналогичен одному из способов превращения круглого диска в двумерную сферу. Если протянуть нитку вдоль края тканевого диска, а затем туго стянуть ее, как будто затягивая торбу, то результат будет топологически идентичен двумерной сфере. А теперь проведите аналогичную операцию с шаром, но не пытайтесь зрительно представить себе результат: просто представьте шар и как бы приложите к нему правила склеивания.

В любом случае Пуанкаре очень интересовался трехмерной сферой, потому что это, предположительно, простейшее трехмерное топологическое пространство конечной протяженности, не имеющее границы. В 1900 г. он опубликовал статью, в которой объявил, что группы гомологий представляют собой достаточно мощный инвариант, чтобы топологически охарактеризовать трехмерную сферу. А именно, если трехмерное топологическое пространство обладает теми же группами гомологий, что и трехмерная сфера, то оно топологически эквивалентно трехмерной сфере (т. е. может непрерывно в нее преобразовываться). К 1904 г., однако, он обнаружил, что это заявление ошибочно. Существует по крайней мере одно трехмерное пространство, которое не является трехмерной сферой, но имеет те же группы гомологий, что и она. Это пространство стало настоящим триумфом подхода, связанного с правилами склеивания, а доказательство того, что это не трехмерная сфера, привело к созданию нового инварианта, заведомо более мощного, чем гомология.

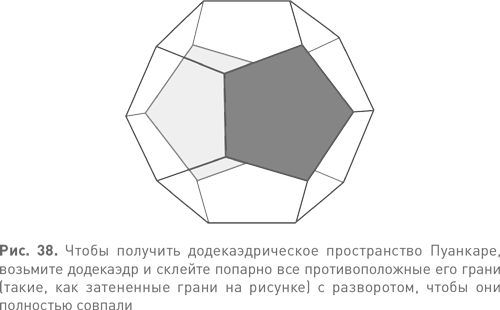
Сначала о пространстве. Оно известно как додекаэдрическое пространство Пуанкаре, потому что в современном построении используется именно заполненный додекаэдр. Пуанкаре не подозревал о родстве своего пространства с додекаэдром. Сам он поступил иначе: склеил два заполненных тора весьма неочевидным способом. Додекаэдрическую интерпретацию опубликовали в 1933 г., через 21 год после смерти Пуанкаре, Герберт Зейферт и Константин Вебер, и она намного проще для понимания. Аналогия, которую здесь следует помнить, это получение тора путем склеивания противоположных сторон квадрата. Как всегда, не нужно пытаться действительно что-то склеить, — достаточно просто помнить, что соответствующие точки рассматриваются именно таким образом. Теперь мы проведем ту же операцию, но возьмем для этого противоположные грани додекаэдра (см. рис. 38).

Пифагорейцы знали о додекаэдре еще 2500 лет назад. Граница додекаэдра состоит из 12 правильных пятиугольников, соединенных в приблизительно сферическую решетку. В каждой его вершине встречаются три пятиугольника. А теперь склеим каждую грань с противоположной… Только для этого их нужно перекрутить. Буквально. Каждую грань, чтобы она совпала с противоположной, нужно повернуть на подходящий угол. Угол берем наименьший из тех, что позволяют совместить соответствующие грани, т. е. 36°. Можно считать это правило своеобразной версией правила изготовления ленты Мёбиуса: конец ленты нужно повернуть на 180°, а затем склеить с противоположным.

Так, пространство получено. А теперь посмотрим на инвариант. Нет, я не растекаюсь мыслью по древу: все это нам потребуется для понимания гипотезы Пуанкаре.

Пуанкаре назвал свой новый инвариант фундаментальной группой. Мы до сих пор пользуемся этим термином, но иногда называем его и иначе: первой гомотопической группой. Гомотопия — это геометрическая конструкция, которая целиком размещается внутри пространства и несет в себе информацию о топологическом типе этого пространства. Она делает это при помощи абстрактной алгебраической структуры, известной как группа. Группа — это набор математических объектов, таких, что комбинация любых двух подобных объектов дает еще один объект той же группы. Для закона комбинирования — его часто называют сложением или умножением, даже если это не те простые операции, которые мы знаем из арифметики — должны выполняться несколько простых и естественных условий. Если мы называем операцию сложением, основные условия такие:

• группа содержит элемент, который ведет себя как нуль: при добавлении к любому другому элементу группы ничего не меняется;

• каждый элемент имеет в группе соответствующий ему элемент с противоположным знаком: при сложении такой пары получается нуль;

• при сложении трех элементов группы не имеет значения, какие два вы складываете первыми. Иными словами, (a + b) + c = a + (b + c). Это называется законом ассоциативности.

Единственный алгебраический закон, который не считается обязательным (хотя иногда и выполняется), — это закон коммутативности a + b = b + a.

Фундаментальная группа Пуанкаре представляет собой своего рода упрощенный скелет пространства. Это топологический инвариант: топологически эквивалентные пространства имеют одну и ту же фундаментальную группу. Чтобы лучше разобраться в этом полезном понятии и, очень может быть, отчасти восстановить мотивы Пуанкаре, посмотрим, как это работает, на примере окружности. Воспользуемся образом, который восходит еще к Гауссу: представьте себе муравья, вся вселенная которого ограничена окружностью. Как он может определить, какой формы его вселенная? Сумеет ли он отличить окружность от, скажем, прямой линии? Не забывайте, что муравей не может выйти за пределы своей вселенной, не может взглянуть на нее со стороны и понять, что она круглая. Он может лишь бродить по вселенной, что бы она собой ни представляла. В частности, муравей не в состоянии понять, что его вселенная изогнута, потому что и свет в ней движется только по кругу. И не обращайте, пожалуйста, внимания на практические сложности, к примеру, на то, что объектам придется, встречаясь, проходить сквозь друг друга, — в любом случае наша аналогия достаточно свободна.

Муравей может определить форму вселенной несколькими способами. Я сосредоточусь на методе, который можно обобщить на любые топологические пространства. Для целей данного обсуждения муравей — точка. Он живет на автобусной остановке, которая тоже представляет собой точку. Каждый день муравей выходит из домика, садится в автобус (который, конечно, тоже точка), а вечером возвращается обратно. Самый простой маршрут — № 0: он просто стоит на остановке и никуда не едет. Для более интересной экскурсии муравей садится в автобус № 1, который объезжает вселенную ровно один раз против часовой стрелки и останавливается, вернувшись домой. Автобус № 2 объезжает вселенную дважды, № 3 — трижды и т. д.; один автобус, движущийся против часовой стрелки, для каждого положительного целого числа. Есть и отрицательные автобусы, которые ездят в противоположном направлении. Автобус № −1 объезжает вселенную один раз по часовой стрелке, № −2 — два раза и т. д.

Муравей быстро замечает, что две последовательные поездки на автобусе № 1, по существу, эквивалентны одной поездке на № 2, а три поездки на № 1 — одной поездке на № 3. Аналогично, следующие одна за другой поездки на автобусах № 5 и № 8 соответствуют одной поездке на автобусе № 13. Более того, для любых двух положительных номеров поездка на автобусе с первым номером плюс следующая за ней поездка на автобусе со вторым номером сводится к поездке на автобусе с номером, соответствующим их сумме.

Следующий шаг тоньше. Примерно то же соотношение сохраняется для автобусов с отрицательными номерами и для № 0. Поездка на № 0 плюс поездка на № 1 очень похожа на поездку на № 1. Однако есть и небольшая разница. В поездке 0 + 1 автобус № 0 некоторое время стоит на остановке, отрабатывая свой маршрут, а в поездке только на № 1 ничего подобного не происходит. Поэтому мы вводим понятие со странным названием гомотопия («то же место» по-гречески). Две петли гомотопичны, если одна из них может быть непрерывно преобразована в другую. Если мы позволим гомотопиям менять расписание автобусов, можно будет постепенно снизить время, которое муравей проводит в стоящем на остановке автобусе № 0, и, в конце концов, период сидения на месте просто исчезнет. Теперь между поездкой 0 + 1 и поездкой 1 нет никакой разницы, так что «с точностью до гомотопии» результат — это просто поездка на автобусе № 1. Иными словами, уравнение для автобусных номеров 0 + 1 = 1 остается верным не для поездок, а для гомотопических классов поездок.

А если за поездкой на автобусе № 1 последует поездка на автобусе № −1? Нам хотелось бы, чтобы в ответе стояла поездка № 0, но это не так. Автобус в этом случае проезжает весь путь сначала против часовой стрелки, а потом — обратно. Это далеко не то же самое, что провести все время поездки в стоящем на остановке автобусе. Поэтому 1 + (−1), т. е. 1−1, не равно 0. На помощь опять же приходит гомотопия. Комбинация автобусов 1 и −1 в целом гомотопна поездке на автобусе 0. Чтобы понять, почему, представьте, что муравей следует по суммарному маршруту автобусов 1 и −1 на автомобиле, но, чуть-чуть не доехав до остановки, разворачивается и едет назад. Такая поездка очень близка к двойной поездке на автобусе: пропущен всего лишь крохотный кусочек маршрута. Таким образом, первоначальное двойное путешествие непрерывно уменьшилось и превратилось в немного более короткую поездку на машине. Теперь муравей может снова чуть-чуть укоротить поездку, повернув назад чуть раньше. Он может таким образом укорачивать поездку, разворачивая автомобиль все раньше и раньше, пока не окажется просто сидящим на остановке. Процесс сжимания поездки — тоже гомотопия. Она показывает, что поездка 1 плюс поездка −1 гомотопна поездке на автобусе № 0. Иными словами, 1 + (−1) = 0 для гомотопических классов поездок.

Теперь любой алгебраист без труда сможет доказать, что поездка на автобусе любого маршрута плюс вторая поездка на каком-нибудь автобусе гомотопна поездке на автобусе, номер которого получается сложением двух автобусных номеров. Это верно для положительных автобусов, для отрицательных автобусов и для автобуса № 0. Так что если мы складываем поездки — или, вернее, гомотопические классы поездок, — то получаем группу. Более того, очень знакомую группу. Ее элементами являются целые числа (номера автобусов), а ее операцией — сложение. Такая группа традиционно обозначается символом Z от немецкого слова Zahl (“целый”).

Гораздо труднее, но все же можно доказать, что в кольцевой вселенной любая кольцевая автомобильная поездка — даже если она предусматривает множество возвратов, отступлений или метаний взад-вперед на одном и том же участке дороги — гомотопична одной из стандартных автобусных поездок. Более того, автобусные поездки с разными номерами не гомотопичны. Доказательство требует некоторых теоретических познаний. Его основа — гауссов порядок кривой, или число вращения. Это число полных обходов окружности против часовой стрелки, которое совершает муравей за всю поездку, и это номер маршрута, которому гомотопична ваша конкретная поездка.

Если заполнить все пробелы и расставить все точки над i, это описание доказывает, что фундаментальная группа окружности совпадает с группой целых чисел Z по операции сложения. Чтобы складывать поездки, нужно просто складывать соответствующие им числа вращения. При помощи этого топологического инварианта муравей может отличить свою кольцевую вселенную от, скажем, бесконечной прямой линии. На прямой любая поездка, как ни мечись, в какой-то момент должна достичь максимально удаленной от дома точки. Тогда мы можем непрерывно сжать поездку, постепенно уменьшая все расстояния от дома в одной и той же пропорции — сначала до 99 %, затем до 98 % и т. д. Поэтому на прямой любая поездка гомотопна нулю: можно просто остаться дома. Фундаментальная группа прямой содержит только один элемент: 0. Ее алгебраические свойства тривиальны: 0 + 0 = 0, и называется она тривиальной группой. А поскольку тривиальная группа не совпадает с группой целых чисел, муравей может понять, живет ли он на прямой или на окружности.

Как я уже говорил, существуют и другие методы, но именно так муравей может заметить разницу при помощи фундаментальной группы Пуанкаре.

А теперь предположим, что наш муравей живет на поверхности и это опять же вся его вселенная. Он не может отойти в сторону и посмотреть, какая именно поверхность является его домом. Может ли он разобраться в топологии своей вселенной? В частности, сможет ли он различить сферу и тор? Ответ по-прежнему «да», а метод тот же, при помощи которого мы исследовали вселенную-окружность: сесть в автобус и совершать круговые поездки, которые начинаются и заканчиваются в одной точке — дома. Чтобы сложить такие поездки, их нужно проделать по очереди — одну за другой. Нулевая поездка — это остаться дома; поездка с обратным знаком — это точно такая же поездка в противоположном направлении. Работая с гомотопическими классами поездок, мы получим группу. Это фундаментальная группа поверхности. По сравнению с вселенной-окружностью здесь куда больше свободы в выборе маршрутов поездок и непрерывном преобразовании их в другие поездки; тем не менее основная идея та же.

Фундаментальная группа здесь тоже является топологическим инвариантом, и муравей может воспользоваться ею, чтобы выяснить, живет ли он на сфере или на торе. Если его вселенная — сфера, то любая поездка, совершенная муравьем, может быть постепенно преобразована в нулевую поездку — пребывание дома. Однако в случае, если вселенная — тор, это не так. Некоторые поездки могут быть преобразованы в нуль, но с поездкой, которая хотя бы раз обойдет вокруг центрального отверстия (см. рис. 39 слева), ничего подобного проделать нельзя. Это утверждение нуждается в доказательстве, но это не проблема. На торе тоже есть стандартные поездки, но теперь номера автобусов представляют собой пары целых чисел (m, n). Первое число m указывает, сколько раз маршрут проходит сквозь центральное отверстие. Второе число n указывает, сколько раз маршрут обвивается вокруг тора. На рис. 39 справа показан маршрут (5, 2), который пять раз проходит сквозь отверстие и дважды обвивается вокруг тора. Чтобы сложить поездки, нужно сложить соответствующие числа маршрутов, к примеру: (3, 6) + (2, 4) = (5, 10). Фундаментальная группа тора — группа пар целых чисел.

Любое топологическое пространство имеет фундаментальную группу, определенную в точности так же, с использованием поездок — или, точнее, петель, — которые начинаются и заканчиваются в одной точке. Пуанкаре придумал фундаментальную группу, чтобы доказать, что его додекаэдрическое пространство не является трехмерной сферой, хотя и имеет те же гомологические инварианты. Его первоначальный метод прекрасно приспособлен к вычислению фундаментальной группы. Более современный метод «скручивания и склеивания» приспособлен к нему еще лучше. Ответом оказывается группа из 120 элементов, связанная с додекаэдром. А вот фундаментальная группа трехмерной сферы, напротив, состоит лишь из одного элемента: нулевой петли. Так что додекаэдрическое пространство топологически не эквивалентно сфере, несмотря на одинаковые группы гомологий, и Пуанкаре доказал, что утверждение, сделанное им в 1900 г., ошибочно.

Пуанкаре продолжал рассуждать о своем новом инварианте: может быть, это и есть недостающий ингредиент топологической характеристики трехмерной сферы? А может, любое трехмерное пространство с той же фундаментальной группой, как у трехмерной сферы, т. е. с тривиальной группой, должно на самом деле быть трехмерной сферой? Он сформулировал это предположение как отрицание в виде вопроса: «Рассмотрим компактное трехмерное многообразие [топологическое пространство] V, не имеющее границы. Возможно ли, чтобы фундаментальная группа многообразия V была тривиальной, хотя V не есть трехмерная сфера [топологически не эквивалентно ей]?» Он оставил вопрос открытым, но очень правдоподобно мнение, что ответ при такой постановке вопроса очевиден — «нет». И вскоре это предположение получило известность как гипотеза Пуанкаре. И столь же быстро стало одним из самых знаменитых открытых вопросов топологии.

Фраза «тривиальная фундаментальная группа» означает, в сущности, что «любая петля может быть непрерывно преобразована в точку». Таким свойством обладает не только трехмерная сфера, но и любая аналогичная ей n-мерная сфера любой размерности n. Так что мы можем выдвинуть точно такое же предположение для сферы любой размерности. Такое утверждение известно как n-мерная гипотеза Пуанкаре. Это верно для n = 2, согласно теореме классификации для поверхностей. И это все, чего удалось достичь математикам за 50 с лишним лет.

В 1961 г. Стивен Смейл взял прием классификации поверхностей и применил его к более высоким измерениям. Один из способов представить себе тор с g отверстиями заключается в том, чтобы взять сферу и приделать к ней мысленно g ручек — точно таких, какие бывают у чайной чашки или кружки. Смейл обобщил это построение для любой размерности и назвал процесс разложением на ручки. Он проанализировал, как могут изменяться ручки при неизменной топологии пространства, и вывел гипотезу Пуанкаре во всех размерностях, больших или равных 7. Для более низких размерностей его доказательство не работало, но другие математики нашли способы с этим справиться: Джон Столлингс провел доказательство для размерности 6, а Кристофер Зиман — для 5. Однако один из существенных этапов доказательства, известный как трюк Уитни, упрямо отказывался работать в размерностях 3 и 4, потому что в таких пространствах просто не хватает места для необходимых маневров, и никто не мог найти эффективной замены этому приему. Постепенно сформировалось мнение о том, что топология пространств для этих двух размерностей может оказаться весьма необычной.

Это мнение, однако, было поколеблено в 1982 г., когда Майкл Фридман получил доказательство четырехмерной гипотезы Пуанкаре, для которого не требовался трюк Уитни. Доказательство было чрезвычайно сложным, но работало. Итак, после 50 лет топтания на месте и 20 лет лихорадочной активности топологи расправились наконец с гипотезой Пуанкаре для всех размерностей, кроме той, о которой, собственно, и шла речь изначально. Успехи впечатляли, но методы, при помощи которых они были достигнуты, не позволяли сказать почти ничего о трехмерном случае. Требовался новый подход.

Перечень того, что позволило, наконец, сдвинуться с мертвой точки, отчасти напоминает традиционный список подарков к свадьбе: что-то старинное, антикварное, что-то новенькое, что-то взятое взаймы и, наконец, если немного выходить за рамки, что-то из даров небес. Старинная идея заключалась в обращении к той области топологии, которая на фоне активной работы с пространствами более высоких размерностей представлялась почти исчерпанной: в топологию поверхностей. Новая идея была в том, чтобы заново рассмотреть классификацию поверхностей с позиции, на первый взгляд, совершенно чуждой: с позиции классической геометрии. Одолженной идеей можно считать поток Риччи, источником вдохновения для которого послужил математический аппарат общей теории относительности Эйнштейна. Ну а к дарам небес можно отнести нечто вроде попадания «пальцем в небо»: далеко идущие предположения, опирающиеся отчасти на интуицию, но куда больше — на надежду.

Вспомним, что ориентируемые поверхности без границы можно проклассифицировать: каждая из них топологически эквивалентна тору с некоторым числом отверстий. Это число — род поверхности, и когда род равен нулю, поверхность представляет собой сферу без ручек, т. е. просто сферу. Это слово сразу же напоминает нам о том, что среди всех топологических сфер одна поверхность стоит особняком и является архетипом. Конкретно речь идет о единичной сфере в евклидовом пространстве. Забудьте на мгновение все разговоры о резиновом листе — пока отложим это в сторону. Сосредоточьтесь на старой доброй евклидовой сфере. У нее много разных дополнительных математических свойств, проистекающих из жесткости и однозначности евклидовой геометрии. Важнейшее из этих свойств — кривизна. Кривизну можно квантифицировать: для каждой точки геометрической поверхности существует число, говорящее о том, насколько изогнута поверхность вблизи этой точки. Сфера — единственная в евклидовом пространстве замкнутая поверхность, кривизна которой во всех точках одинакова и положительна.

Это странно, потому что постоянная кривизна — не топологическое свойство. Еще загадочнее то, что сфера не одинока. Существует еще одна стандартная геометрическая поверхность, которая стоит особняком и представляет собой архетипический тор. А именно: начнем с квадрата на плоскости и отождествим противоположные его стороны (см. рис. 12 из главы 4). Результат в трехмерном пространстве после скатывания рулона и соединения тождественных сторон выглядит изогнутым. Однако, по существу, мы можем работать непосредственно с квадратом, применив дополнительно правила склеивания. Квадрат имеет естественную геометрическую структуру: это участок на евклидовой плоскости. Плоскость, кстати говоря, тоже имеет постоянную кривизну, на этот раз нулевую. Тор с данной конкретной геометрией тоже имеет нулевую кривизну и называется плоским тором. Возможно, название звучит как оксюморон, но для муравья, живущего на плоском торе и пользующегося линейкой и транспортиром для измерения расстояний и углов, местная геометрия вполне соответствовала бы плоской геометрии.

Геометры XVIII в., стараясь разобраться в аксиоме Евклида о существовании параллельных линий, пытались вывести ее из остальных евклидовых постулатов, но раз за разом терпели поражение. В конце концов пришло понимание, что такой вывод невозможен. Существует три различных типа геометрии, в каждом из которых выполняются все условия и требования Евклида, за исключением аксиомы о параллельных прямых. В настоящее время эти геометрии известны как евклидова (это плоскость, на которой аксиома о параллельных прямых верна), эллиптическая (геометрия на поверхности сферы с некоторыми финтифлюшками: здесь две прямые всегда пересекаются, а параллельной прямой не существует) и гиперболическая геометрия (где некоторые прямые не пересекаются, а параллельная прямая не единственна). Более того, классические математики интерпретируют эти геометрии как геометрии искривленных пространств. Евклидова геометрия соответствует нулевой кривизне, эллиптическая/сферическая геометрия — постоянной положительной кривизне, а гиперболическая геометрия — постоянной отрицательной кривизне.

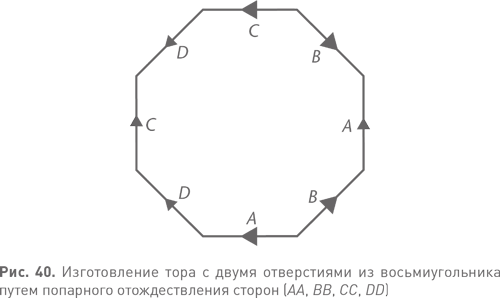
Мы только что видели, как можно получить две из трех перечисленных геометрий: они возникают на сфере и на плоском торе. В терминах теоремы классификации это торы рода g для g = 0 и 1. Единственное, чего у нас пока не хватает, это гиперболической геометрии. Может быть, каждый тор с g дырками обладает естественной геометрической структурой, основанной на том, что в гиперболическом пространстве взяли некий многоугольник и отождествили у него некоторые стороны? Ответ поразителен: «да» для любой величины g, большей или равной 2. На рис. 40 показан пример для g = 2 на основе восьмиугольника. Я опущу гиперболическую геометрию и идентификацию этой поверхности как двумерного тора, но скажу, что разобраться в этом можно. Различные g возникают, если мы берем разные многоугольники, но исключений нет — можно получить любой g. Используя профессиональную лексику, скажем, что тор с двумя и более дырками имеет естественную гиперболическую структуру. Теперь можно пересмотреть список стандартных поверхностей:

• сфера: g = 0 — эллиптическая геометрия;

• тор: g = 1 — евклидова геометрия;

• тор с g дырками: g = 2, 3, 4… — гиперболическая геометрия.

Может показаться, что мы выплеснули с водой и ребенка, ведь топология должна иметь дело с геометрией на резиновом листе, а не с жесткой геометрией. Но теперь мы легко можем вернуть резину на место. Жесткая геометрия используется здесь только для того, чтобы определить стандартные поверхности. Она позволяет дать простые описания, которые оказываются еще более жесткими. А теперь ослабим жесткость, т. е. позволим пространству стать резиновым и разрешим деформироваться, что невозможно при жесткой структуре. При этом мы получим поверхности, топологически эквивалентные стандартным, но не получаемые из них путем жестких сдвигов. Согласно теореме о классификации, таким образом можно получить любую топологическую поверхность.

Топологи знали о существовании такой связи между геометрией и теоремой о классификации поверхностей, но в то время она представлялась забавным совпадением, дающим, несомненно, весьма ограниченные возможности в двух измерениях. Все понимали, что трехмерный случай намного богаче и, в частности, пространствами постоянной кривизны его возможности не исчерпываются. Но понять, что жесткая геометрия может оказаться полезной при рассмотрении трехмерной топологии, сумел лишь Уильям Терстон — один из лучших геометров мира. Несколько указаний на это уже имелось: трехмерная сфера Пуанкаре, исходя из ее определения, обладает естественной эллиптической/сферической геометрией. Хотя стандартный додекаэдр обитает в евклидовом пространстве, угол между его смежными гранями меньше 120°, так что три таких угла не образуют полной окружности. Чтобы исправить это, нам придется слегка надуть додекаэдр, чтобы его грани стали немного выпуклыми: это сразу превращает естественную геометрию фигуры из евклидовой в сферическую. Аналогично, треугольники на сфере тоже становятся выпуклыми. Трехмерный тор, полученный путем отождествления противоположных граней куба, обладает плоской, т. е. евклидовой, геометрией, в точности так же, как его двумерный аналог. Макс Ден и другие исследователи открыли несколько трехмерных топологических пространств, обладающих естественной гиперболической геометрией.

У Терстона появились первые подозрения о возможности существования общей теории, но, чтобы она обрела хотя бы относительную правдоподобность, требовались два нововведения. Во-первых, необходимо было расширить диапазон трехмерных геометрий. Исходя из здравого смысла, Терстон сформулировал некоторые условия и выяснил, что им удовлетворяет ровным счетом восемь геометрий. Три из них — это классика: сферическая, евклидова и гиперболическая геометрия. Еще две напоминают цилиндры: плоские в одном направлении, изогнутые в двух других. Изогнутая часть имеет либо положительную кривизну, как у двумерной сферы, либо отрицательную, как у гиперболической плоскости. Наконец, есть еще три, достаточно формальные, геометрии.

Во-вторых, было ясно, что некоторые трехмерные пространства не поддерживают ни одну из восьми геометрий. Но нашелся и выход: разрезать пространство на куски. Один кусок, возможно, обладает сферической геометрической структурой, другой — гиперболической и т. д. Чтобы разрезание было полезным, его надо проводить по очень строгим правилам, чтобы обратный процесс — собирание кусков в единое целое — позволил получить полезную информацию. Хорошей новостью стало то, что во многих случаях это возможно. В 1982 г. Терстон в приступе вдохновения сформулировал гипотезу о геометризации: любое трехмерное пространство может быть разрезано на куски, каждый из которых обладает естественной геометрической структурой, соответствующей одной из восьми возможных геометрий. Он доказал также, что если его гипотеза о геометризации верна, то гипотеза Пуанкаре окажется простым ее следствием.

Тем временем появилось и второе направление атаки, тоже геометрическое и тоже основанное на кривизне, но исходящее из совершенно иной области: математической физики. Гаусс, Риман и целая школа итальянских геометров создали общую теорию искривленных пространств, получивших название многообразий, причем концепция расстояния у них необыкновенно расширила и евклидову, и классическую неевклидову геометрию. Кривизна уже не обязана быть постоянной: она может плавно меняться от одного конца к другому. К примеру, фигура, напоминающая собачью косточку, имеет положительную кривизну на концах, но отрицательную посередине, и величина кривизны изменяется плавно от одного участка к другому. Кривизна квантифицируется при помощи математических инструментов, известных как тензоры. Около 1915 г. Альберт Эйнштейн понял, что тензоры кривизны — это именно то, чего ему не хватало для расширения специальной теории относительности, описывающей пространственно-временные отношения, до общей теории относительности, включающей также и гравитацию. В этой теории гравитационное поле представлено как кривизна пространства, а эйнштейновы уравнения поля описывают, как соответствующая мера кривизны — тензор кривизны — изменяется в зависимости от распределения материи. В результате кривизна пространства плывет со временем; вселенная или некая ее часть спонтанно меняет форму.

Ричард Гамильтон, специалист по римановой геометрии, понял, что тот же фокус можно применить в более общем плане и что результатом этого может стать доказательство гипотезы Пуанкаре. Идея состояла в том, чтобы работать с одной из простейших мер кривизны, именуемой кривизной Риччи в честь итальянского геометра Грегорио Риччи-Курбастро. Гамильтон записал уравнение, определявшее, как кривизна Риччи должна изменяться со временем: уравнение потока Риччи. Согласно этому уравнению, кривизна должна была постепенно перераспределиться и стать как можно более равномерной. Картина немного напоминает кошку под ковром из главы 4, но теперь кошка, хотя и не может сбежать, способна растечься по полу ровным слоем. (Говоря иначе, кошка здесь должна быть топологической.)

К примеру, в двумерном случае начнем с грушевидной поверхности (см. рис. 41). На одном конце она имеет область сильной положительной кривизны. Область на другом, более толстом конце тоже положительно искривлена, но не так сильно, а в промежутке грушу опоясывает область с отрицательной кривизной. По существу, поток Риччи переносит кривизну с сильно искривленного конца (и в меньшей степени с другого конца) в отрицательно искривленную область до тех пор, пока вся отрицательная кривизна не будет поглощена. На этой стадии результат — бугристая поверхность с повсеместно положительной кривизной. Поток Риччи продолжает перераспределять кривизну, забирая ее из сильно искривленных областей и перенося в менее искривленные. Время идет, и поверхность становится все ближе и ближе к той единственной форме, что имеет постоянную положительную кривизну, т. е. к евклидовой сфере. Топология остается прежней, хотя форма, если посмотреть подробнее, меняется. Следуя потоку Риччи, можно доказать что первоначальная грушевидная поверхность топологически эквивалентна сфере.

В этом примере топологический тип поверхности был очевиден с самого начала, однако та же общая стратегия действует для любого многообразия. Начните со сложной формы и следуйте за потоком Риччи. Со временем кривизна перераспределяется более равномерно, и форма упрощается. В конце концов вы должны получить простейшую форму с той же топологией, что и у первоначального многообразия, какой бы эта топология ни была. В 1981 г. Гамильтон доказал, что такая стратегия работает в двух измерениях, обеспечивая новое доказательство теоремы о классификации для поверхностей.

Кроме того, он добился значительного прогресса в аналогичной стратегии для трехмерных многообразий, но здесь возникло серьезное препятствие. В двух измерениях любая поверхность автоматически упрощается, следуя потоку Риччи. Это верно и в трех измерениях, если первоначальное многообразие во всех точках имеет строго положительную кривизну и нигде — нулевую или отрицательную. К несчастью, если в многообразии есть точки с нулевой кривизной — а они часто есть, — пространство, двигаясь в потоке, может запутаться. При этом возникают сингулярности — места, где многообразие перестает быть гладким. В таких точках уравнение потока Риччи не работает, и перераспределение кривизны прекращается. Естественный способ обойти это препятствие заключается в том, чтобы понять, что представляют собой сингулярности, и изменить многообразие — может быть, разрезать его на куски, чтобы можно было дать стартовый толчок потоку Риччи. Такая стратегия может оказаться успешной, если вы в достаточной степени контролируете связь топологии измененного многообразия к первоначальной. К несчастью, Гамильтон понял также, что для трехмерных пространств сингулярности потока Риччи могут быть чрезвычайно сложными — судя по всему, слишком сложными, чтобы применять подобные уловки. В общем, поток Риччи быстро стал в геометрии стандартным методом, но для доказательства гипотезы Пуанкаре его не хватило.

К 2000 г. гипотеза по-прежнему оставалась не доказанной; после вхождения в число семи проблем тысячелетия она приобрела еще более широкую известность и признание. К тому моменту стало ясно, что если каким-то образом удастся все же добиться, чтобы идея Гамильтона сработала, то тем самым будет доказана не только гипотеза Пуанкаре, но и гипотеза Терстона о геометризации. Приз был соблазнителен и близок, но в руки не давался.

В математике, как и в остальных отраслях науки, работа, чтобы ее признали, должна быть опубликована, а для этого — пройти рецензирование. Специалисты в соответствующей области должны внимательно прочитать работу, проверить логические выкладки и убедиться в безошибочности вычислений. Для сложной и значительной математической работы этот процесс может занять немало времени. Как упоминалось в главе 4, раньше выходом в каких-то ситуациях становился препринт, но сегодня существует стандартный веб-сайт arXiv.org, своеобразный архив, где после частичного рассмотрения и утверждения (чтобы отсечь всякие глупости) разрешается размещать электронные препринты. В настоящее время большинство исследователей знакомится с новыми результатами на сайте arXiv или на собственном сайте автора.

В 2002 г. Григорий Перельман разместил на сайте arXiv препринт о потоке Риччи. В работе было сделано замечательное утверждение: поток Риччи градиентоподобен. Иными словами, существует вполне определенное направление вниз — единственная числовая величина, связанная с формой многообразия, и многообразие всегда течет вниз в том смысле, что эта величина всегда уменьшается со временем. Она чем-то напоминает высоту в ландшафте и позволяет количественно оценить «упрощение» многообразия. Градиентоподобные потоки имеют немало ограничений: к примеру, они не могут ходить кругами или вести себя хаотично. Никто, похоже, не подозревал, что поток Риччи окажется таким ручным. Но Перельман не просто выдвинул предположение: он доказал это. В конце он наметил цепочку рассуждений, которые должны были бы доказать гипотезу Терстона о геометризации — а она, если помните, подразумевает гипотезу Пуанкаре, но заходит на самом деле гораздо дальше, — и пообещал подробнее изложить все это в следующих статьях на сайте arXiv. В течение следующих восьми месяцев он разместил там две статьи, содержавшие большую часть обещанных подробностей.

Первая статья вызвала немалый переполох. Перельман утверждал, что ему удалось реализовать всю программу Гамильтона — использовать поток Риччи для упрощения трехмерного многообразия и доказать, что результат получился в точности таким, как предсказывал Терстон. Две другие статьи добавили рассуждениям Перельмана убедительности: у математиков возникло чувство, что это человек знает, о чем говорит, и что его идеи — не просто очередная правдоподобная стратегия с неизменной логической прорехой или недоказанным допущением. Обычный скепсис математического сообщества по отношению к любым заявлениям о решении одной из великих задач слегка поутих. Возникло ощущение, что его попытка вполне может увенчаться успехом.

Однако дьявол, как всегда, кроется в деталях, а в математике детали бывают дьявольски непокорными! Работу необходимо было проверить, не спеша и на полную глубину, причем сделать это должны были те, кто разбирается в соответствующих областях и в состоянии распознать потенциальные ловушки. А это было непросто, поскольку Перельман в своей работе свел воедино по крайней мере четыре очень разные области математики и математической физики, а мало кто из математиков может похвастать знаниями более чем в одной-двух областях. Анализ корректности его доказательства потребовал бы много усилий и командной работы. Более того, в препринтах на сайте arXiv не было всех подробностей, необходимых в публикуемой статье. Для препринтов они были написаны довольно ясно, но точки над i там были расставлены не все. Так что экспертам нужно было реконструировать часть рассуждений Перельмана — при том, что сам-то он занимался этой работой несколько лет!

На все это требовалось время. Перельман читал лекции по своему доказательству и отвечал по электронной почте на вопросы, касавшиеся различных его этапов. Всякий раз, как кто-нибудь находил кажущуюся прореху, он быстро откликался, объяснял необходимое и заполнял пробелы. Все выглядело обнадеживающе. Однако никто не собирался рисковать репутацией и заявлять публично, что Перельман доказал гипотезу Пуанкаре и, тем паче, еще более сложную гипотезу о геометризации. Нужна была полная уверенность в том, что доказательство безошибочно. Поэтому, несмотря на общее благосклонное отношение к работе Перельмана, публичного признания она поначалу не получила. Это было ожидаемо, но время шло, и Перельмана все больше охватывало раздражение, потому что, как ему казалось, он впустую тратил время. Он-то знал, что его доказательство верно, и не мог понять, почему у остальных возникают такие сложности. Он отказался написать о своей работе подробнее или представить статью в какой-нибудь журнал. С его точки зрения, дело было сделано, а препринты на arXiv содержали всю необходимую информацию. Он перестал отвечать на вопросы, касавшиеся недостающих вроде бы деталей. Для него все было очевидно. Да ладно, ребята, вы и сами можете разобраться в этом, без моей помощи. Это не так уж сложно.

Некоторые писали, что математическое сообщество было несправедливо к Перельману. Но те, кто так говорят, просто не понимают, как принято действовать, когда появляется заявка на решение одной из великих задач. Было бы безответственно просто похлопать автора по плечу, сказать: «Отлично! Молодец!» — и забыть о том, чего не хватает в его препринтах. Вполне справедливо было попросить его подготовить более подробное изложение доказательства, пригодное для публикации. Когда речь идет о столь важной задаче, спешить нельзя. Специалисты из кожи вон лезли, тратили кучу времени на доказательство Перельмана и больше обычного старались сдержать свой естественный скептицизм. Сказать по правде, к автору отнеслись даже более благожелательно, чем обычно. И со временем, когда процесс проверки был завершен, его работу приняли и признали.

К этому моменту, однако, Перельман успел потерять терпение. Возможно, сказалось и то, что решенная им задача была настолько значительной, что ничто, по существу, уже не могло с ней сравниться. Он был как альпинист, сумевший подняться на Эверест в одиночку и без кислорода. Сравнимых вызовов просто не осталось. Успех в средствах массовой информации его не прельщал: он ждал признания со стороны равных, а не со стороны телеведущих всех сортов. Потому можно понять, почему, когда коллеги наконец признали, что он прав и предложили ему Филдсовскую медаль и премию Института Клэя, он не захотел принять эти награды.

Доказательство Перельмана отличается глубиной и элегантностью и открывает перед исследователями целый новый мир топологии. Автор сумел реализовать план Гамильтона по потоку Риччи, придумав хитрые способы обойти существование сингулярностей. Один из таких способов заключается в том, чтобы изменить масштабы пространства и времени и таким образом избавиться от сингулярности. Когда такой подход не работает, говорят, что сингулярность схлопывается. В подобных случаях Перельман анализирует геометрию потока Риччи в подробностях и разбирает, как именно может произойти схлопывание. По существу, пространство как бы выпускает бесконечно тонкие щупальца, иногда во множестве, как ветви дерева. Если какая-то ветка близка к схлопыванию, ее можно срезать и заменить гладкой крышечкой. Перед некоторыми из этих щупальцев поток Риччи буксует: если так, оставляем их в покое. Если же нет, поток Риччи можно запустить заново. В итоге некоторые щупальца заменяются гладкими крышками, а другие временно прерываются, но поток продолжает работать.

Процедура срезания и замазывания щупалец рубит пространство примерно так же, как терстоново рассечение на куски, каждый со своей геометрией (одной из восьми). Оказывается, что обе процедуры приводят к более или менее одинаковым результатам. Но есть один принципиально важный технический момент: операция обрезки не должна бесконечно ускоряться, так чтобы за конечное время проводилось бесконечное число операций. Это часть доказательства — одна из сложнейших.

Некоторые комментаторы критикуют математическое сообщество за несправедливое отношение к Перельману. Конечно, никто не должен быть закрыт для критики, да и инциденты, в которых, в принципе, можно разглядеть несправедливость или по крайней мере необдуманность, действительно имели место, но в целом математическое сообщество отреагировало на работу Перельмана быстро и положительно. Кроме того, реакция была осторожной, что абсолютно естественно в математике и науке вообще, и не без причин. Неизбежная публичность и слава, еще более яркая благодаря премии в миллион долларов, сказалась бы на любом человеке, и Перельман не исключение.

С момента размещения первой статьи Перельмана на arXiv в ноябре 2002 г. до объявления в марте 2010 г. о присуждении ему премии Института Клэя прошло восемь лет. Кажется, что это серьезная и, возможно, безосновательная задержка. Однако та, первая, публикация содержала лишь часть доказательства. Остальное по большей части было размещено на сайте в марте 2003 г. К сентябрю 2004 г., полтора года спустя после этой второй публикации, сообщество специалистов по потоку Риччи и топологии успело проработать доказательство — следует отметить, что этот процесс начался всего через несколько дней после первой публикации, — и ведущие эксперты объявили, что «поняли его». Они нашли в нем ошибки, нашли пробелы, но выразили уверенность в том, что все это можно исправить. Полтора года — совсем немного, когда речь идет о таком важном вопросе.

В конце 2005 г. Международный математический союз связался с Перельманом и предложил ему Филдсовскую премию, высшую математическую награду. Присудить ее предполагалось на Международном математическом конгрессе в 2006 г. Конгресс проводится раз в четыре года, так что это была бы первая возможность почтить ученого за серьезное достижение. Поскольку в полноте доказательства гипотезы Пуанкаре оставались некоторые сомнения — в нем все еще время от времени обнаруживались ошибки, — премия официально присуждалась за успехи в понимании потока Риччи (эта часть препринтов Перельмана к тому моменту уже считалась свободной от ошибок).

Условия присуждения премии за решение проблем тысячелетия размещены на сайте Института Клэя. В частности, предлагаемое решение должно быть опубликовано в рецензируемом журнале и принято математическим сообществом, причем отношение к нему не должно измениться за два года после публикации. После этого специальный консультативный комитет должен рассмотреть вопрос и выдать рекомендацию: присуждать автору премию или нет. Перельман не выполнил первого условия и, судя по всему, никогда уже этого не сделает. С его точки зрения, препринтов на сайте arXiv достаточно. Тем не менее Институт Клэя махнул на это рукой и объявил о начале уставного двухлетнего срока: требовалось посмотреть, не всплывут ли еще какие-нибудь ошибки или вопросы. Срок истек в 2008 г.; теперь нужно было следовать строгой (чтобы, не дай бог, не выдать премию преждевременно) процедуре.

Это правда, что некоторые эксперты не спешили выражать свою уверенность в корректности доказательства Перельмана. Причина понятна: они действительно не были в ней уверены. Не будет преувеличением сказать, что единственным человеком, способным быстро разобраться в доказательстве Перельмана, мог бы быть только второй Перельман. Невозможно читать математическое доказательство с листа, как музыканты читают ноты. Необходимо убедить самого себя в том, что здесь все разумно и имеет смысл. Всякий раз, когда аргументация усложняется, ты понимаешь, что возрастает и вероятность ошибки. То же можно сказать и о ситуации, когда излагаемые идеи становятся слишком простыми: многие перспективные доказательства споткнулись на утверждениях настолько очевидных, что ничего доказывать, казалось бы, вообще не требовалось. До тех пор, пока эксперты не убедились окончательно в том, что доказательство верно в своей основе — а именно в этот момент они признали достижение Перельмана, несмотря на оставшиеся пробелы и ошибки, — разумно было воздержаться от суждений. Вспомните, к примеру, шумиху вокруг холодного синтеза, данные о котором через некоторое время были опровергнуты. Осторожность — верная профессиональная реакция, и в данном случае вполне применимо известное изречение: чрезвычайные заявления требуют чрезвычайных доказательств.

Почему же Перельман отверг Филдсовскую премию и отказался от награды Института Клэя? Это известно лишь ему самому, но вообще-то его никогда не интересовало признание такого рода, и он не раз говорил об этом. Он и раньше отказывался от премий и призов, правда, не таких престижных и крупных. Перельман с самого начала дал понять, что не хочет преждевременной известности. По иронии судьбы, именно это стало одной из причин, по которым специалисты не спешили высказывать свое мнение. Но, по правде говоря, не было ни единого шанса на то, что средства массовой информации не заметят его работу. Много лет математическое сообщество всеми силами старалось заинтересовать этой темой газеты, радио и телевидение, и нет смысла жаловаться на то, что эти усилия увенчались успехом, или ждать, что СМИ пропустят самую громкую математическую сенсацию со времен Великой теоремы Ферма. Но Перельман смотрел на все это иначе и спрятался в раковину. Поступило предложение — и оно остается в силе — использовать премиальные деньги на образовательные или иные цели, если он согласится. До сих пор ответа на это предложение нет.