Как выиграть в лотерею?

Книга: Тайны чисел: Математическая одиссея

Назад: Насколько вы сильны в случайности?

Дальше: Как обманывать в покере и показывать фокусы, используя задачу о простых числах на миллион долларов

Этот вопрос чаще всего задают мне, когда я говорю, что провожу свою жизнь в играх с числами. Но, как и при подбрасывании монеты, числа, выпавшие в розыгрыше предыдущей недели, не могут повлиять на числа ближайшей субботы. В этом и состоит принцип случайности, но некоторых людей не убедить никогда.

Розыгрыши итальянской государственной лотереи проводятся два раза в неделю, они проходят в десяти городах страны. Участники выбирают числа от 1 до 90. В какой-то момент шар с номером 53 отказывался выпадать в Венеции на протяжении почти двух лет розыгрышей. Разумеется, после столь долгого отсутствия он наверняка выпадет на следующей неделе – так думали многие итальянцы. Одна женщина поставила все сбережения своей семьи на то, что выпадет шар с номером 53. Когда он снова не появился, женщина утопилась в море. Были и другие трагические случаи, например когда мужчина застрелил свою семью, а потом убил себя. У него образовался огромный долг после того, как он поставил на шар 53. Как оценивается, итальянцы вложили £ 2,4 миллиарда – в среднем £ 150 на семью – в ставки, что выпадет 53.

Были даже призывы к правительству запретить номер 53 в лотерее, чтобы положить конец общенациональной одержимости этим числом. Когда плотина наконец-то была прорвана, и 9 февраля 2005 г. шар 53 показался в розыгрыше, было выплачено £ 400 миллионов неназванному числу игроков. С неизбежностью нашлись те, кто обвинил правительство в подтасовке лотереи, чтобы не проводить огромные выплаты. Подобный слух циркулировал не впервые. В 1941 г. шар с номером 8 не появился после 201 розыгрыша в Риме. Многие полагали, что Муссолини подтасовал его невыпадение, чтобы направить ставки нации на шар номер 8 на финансирование итальянских военных расходов.

А теперь давайте проверим, насколько вы удачливы, и сыграем в нашу маленькую лотерею. Я не могу обещать вам миллионы фунтов, но зато участие в ней не будет вам стоить ничего. Чтобы сыграть в лотерею, сначала выберите 6 из 49 чисел билета (рис. 3.02).

Рис. 3.02. Лотерея «Тайн 4исел»

Выбрали числа? Чтобы посмотреть, оказались ли они выигрышными, зайдите на веб-сайт .

Чтобы проверить, выиграли ли вы, зайдите на веб-сайт, приведенный выше в тексте в рамке. Выберите 1 ticket, United Kindom and National Lottery (1 билет, Соединенное Королевство и Национальная лотерея), а затем щелкните «Pick Tickets» – «Вытянуть билеты». Если у вас нет доступа к интернету, то посмотрите на заранее выбранные шесть чисел в конце этой главы. Только не надо жульничать. Как и при решении математических головоломок, вы получите значительно большее удовольствие, если получите ответ сами, а не подглядите его.

Каков ваш шанс выбрать правильно все шесть чисел и выиграть в лотерею? Чтобы сосчитать вероятность, нужно найти число всех различных способов выбрать 6 чисел, назовем это число N. Тогда у вас будет 1 шанс из N выиграть в лотерею. Для разогрева давайте найдем число различных способов выбрать 2 числа. У вас есть 49 вариантов для вашего первого числа. Второе число вы можете выбрать 48 способами. Каждый выбор первого числа может сочетаться с одним из 48 оставшихся чисел. Итак, у вас имеется 49 × 48 различных пар чисел. Но постойте, ведь каждый выбор был сосчитан дважды. Например, если вы выбрали 27 в качестве вашего первого числа, а затем 23 в качестве второго, то получится то же самое, если вы выбрали 23 первым, а 27 вторым. Итак, возможных пар в 2 раза меньше, чем вы подумали сначала, что означает, что число пар, которые вы можете выбрать, равно ½ × 49 × 48.

Теперь перейдем к шести числам. Имеется 49 вариантов выбора первого числа, 48 второго, 47 третьего, 46 четвертого, 45 пятого и, наконец, 44 варианта выбора последнего числа. Что дает 49 × 48 × 47 × 46 × 45 × 44 комбинаций шести чисел. Однако мы опять учли каждую комбинацию более одного раза. Например, сколько раз мы сосчитали комбинацию 1, 2, 3, 4, 5, 6? Что же, мы могли выбрать в качестве первого любое из этих шести чисел (и выбрали, скажем, 5). Тогда у нас останется пять возможных способов выбрать второе число (скажем, 1), четыре варианта для следующего числа (скажем, 2), три для последующего (скажем, 6), два для предпоследнего числа (скажем, 4), а последнее число – единственное, которое осталось (в данном случае 3). Итак, имеется 6 × 5 × 4 × 3 × 2 × 1 различных способов выбрать шесть чисел 1, 2, 3, 4, 5, 6. То же самое относится к любой комбинации шести чисел. Значит, нам нужно разделить 49 × 48 × 47 × 46 × 45 × 44 на 6 × 5 × 4 × 3 × 2 × 1, чтобы получить правильное число всех возможных вариантов заполнить наш лотерейный билет. И каков ответ? 13 983 816.

Это число определяет также ваш шанс выиграть, потому что оно дает число всех возможных комбинаций шаров при розыгрыше. Другими словами, ваш шанс выбрать правильную комбинацию среди всех возможных будет 1 из 13 983 816.

А какова вероятность того, что вы не угадали ни одно число? Мы можем найти ее тем же способом, как и ранее. Ваше первое число должно быть одним из 43 невыпавших, второе число – одним из остающихся 42 и т. д. Это дает 43 × 42 × 41 × 40 × 39 × 38 разных комбинаций. Но каждая из комбинаций была учтена 6 × 5 × 4 × 3 × 2 × 1 раз. Итак, число всех комбинаций, в которых нет ни одного правильного числа, равно 43 × 42 × 41 × 40 × 39 × 38, поделенному на 6 × 5 × 4 × 3 × 2 × 1, или 6 096 454. Итак, у чуть менее чем половины всех возможных выборов нет ни одного выигрышного числа. Чтобы сосчитать ваш шанс не угадать ни одного числа, нужно разделить 6 096 454 на 13 983 816. Это приблизительно равно 0,436, другими словами, вероятность того, что вы не угадаете ничего, составляет 43,6 %.

Итак, у вас есть шанс 56,4 % угадать хотя бы одно число. А каков шанс, что у вас будет ровно два верных числа? Чтобы найти его, нужно сначала определить количество комбинаций с двумя верными числами. У вас есть выбор из шести для одного правильного числа и выбор из пяти для второго правильного числа. Получается 6 × 5, но это число опять нужно разделить на 2 в силу двойного учета. Для четырех неверных чисел у вас имеется 43 × 42 × 41 × 40 комбинаций, что нужно разделить на 4 × 3 × 2 × 1 из-за многократного учета. Значит, количество комбинаций, в которых верны ровно два числа, составляет

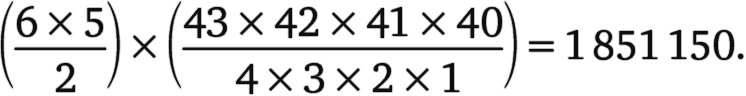
В таблице 3.01 приведены ваши шансы угадать правильно от 0 до шести чисел, все вероятности рассчитаны таким же способом. Чтобы представить эти числа в перспективе, отметим, что если вы будете покупать билет национальной лотереи каждую неделю, то примерно через год вы можете ожидать, что у одного из ваших билетов будут по крайней мере три правильных числа. Примерно через двадцать лет вы могли бы увидеть билет по крайней мере с четырьмя верными числами. Король Альфред, покупай он билет каждую неделю, смог бы к настоящему времени увидеть один билет с пятью выигравшими числами. А если бы первой мыслью, появившейся в голове первого Homo sapiens, была бы идея зайти в ближайший киоск и начать покупать один лотерейный билет каждую неделю, то к настоящему времени он мог бы выиграть один большой приз.

Таблица 3.01. Шанс правильно угадать от 0 до 6 номеров национальной лотереи

Почему числа любят собираться вместе

Ниже приведен способ расчета количества лотерейных билетов, у которых есть хотя бы два последовательных числа. Математики часто применяют хитроумный трюк, состоящий в решении противоположной задачи, это мы сейчас и сделаем. Сначала мы сосчитаем количество билетов без последовательных чисел, затем вычтем результат из полного числа возможных комбинаций, чтобы найти, у какого количества комбинаций будут последовательные числа.

Сначала выберите любые шесть чисел от 1 до 44 (заметьте, что разрешается выбирать именно до 44, а не до 49, вскоре вы поймете почему). Назовите ваш выбор чисел А(1), …, А(6), причем число А(1) – меньшее из выбранных, а А(6) – самое большое. Хотя числа А(1) и А(2) могут быть последовательными, числа А(1) и А(2) + 1 уже не будут таковыми. Так что, если вы возьмете шесть чисел A(1), A(2) + 1, A(3) + 2, A(4) + 3, A(5) + 4 и A(6) + 5, никакие два из них не будут последовательными. (Ограничение на выбор чисел до 44 теперь становится понятным, потому что если А(6) равно 44, то А(6) + 5 равняется 49.)

Используя этот трюк, вы можете сгенерировать все билеты без последовательных чисел. То есть вы просто выбираете шесть чисел от 1 до 44 и разрежаете их, увеличивая каждое из них. Значит, мы найдем число возможных комбинаций, в которых нет последовательных чисел, и оно будет таким же, как число возможных комбинаций по выбору шести чисел от 1 до 44. Последнее равно

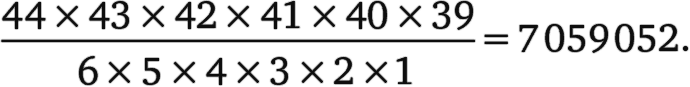
Итак, полное количество билетов с последовательными числами будет

13 983 816 – 7 059 052 = 6 924 764.

Если вам когда-либо настолько повезет, что вы выиграете большой приз, вам не захочется, чтобы произошло то, что случилось в Великобритании 14 января 1995 г. Тогда шла лишь девятая неделя национальной лотереи, а джекпот превзошел немалую сумму в £ 16 миллионов. Когда шесть шаров выпали из лототрона, то победители наверняка прыгали у диванов и кричали от счастья. Но когда они пришли за выигрышем, то каждый из них обнаружил, что ему придется поделить джекпот с другими 132 обладателями счастливых билетов. Каждый из победителей получил пустяк в £ 122 510.

Но как получилось, что так много людей угадали правильную комбинацию? Дело заключается в том обстоятельстве, которое я отметил, когда мы рассматривали игру «Камень, ножницы, бумага»: мы, люди, печально известны своим неумением выбирать случайные числа. Нужно принять во внимание, что 14 миллионов человек играют в национальную лотерею, и многих из них притягивают схожие числа, например число удачи 7 либо дни рождений или юбилеев (что исключает числа 32–49). Также для выбора многих людей характерно то, что они стремятся распределить свои числа равномерно.

Вот выигравшие числа девятой недели лотереи:

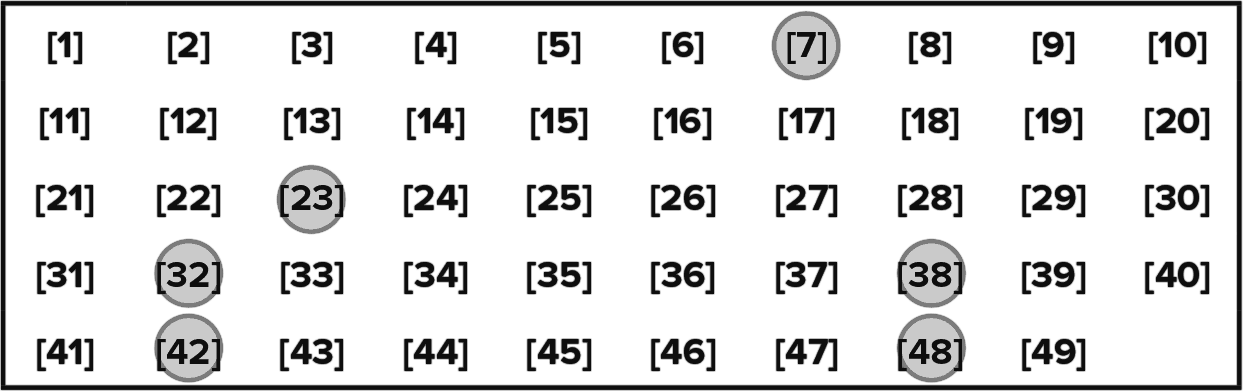
Рис. 3.03

Такое равномерное распределение чисел не слишком-то характерно для случайных процессов: числа могут собираться вместе и отталкиваться с одинаковой вероятностью. Из 13 983 816 различных возможных комбинаций лотерейных билетов у 6 924 764 будут хотя бы два последовательных номера. Это составляет 49,5 %, что очень близко к половине всех комбинаций. Например, в предшествовавшую неделю выпали номера 21 и 22. А в последовавшую неделю были 30 и 31.

Однако не привязывайтесь слишком к последовательным числам. Вы могли бы решить, что комбинация 1, 2, 3, 4, 5, 6 будет умным выбором. В любом случае, как я надеюсь, к настоящему времени вы понимаете, что эта комбинация столь же вероятна, как и любая другая (то есть крайне маловероятна). Если вы сорвете джекпот с этой комбинацией, вы, наверное, рассчитываете получить выигрыш целиком. Но, оказывается, более 10 000 человек в Великобритании используют эту комбинацию каждую неделю – что лишь показывает, насколько разумно британское население. Единственная проблема состоит в том, что в случае выигрыша вам придется делиться джекпотом с другими 10 000 умными людьми.

Назад: Насколько вы сильны в случайности?

Дальше: Как обманывать в покере и показывать фокусы, используя задачу о простых числах на миллион долларов