Четкое следование динамики роста многих «быстрых» фирм почти совершенной экспоненте вселяет надежду на успех моделирования соответствующего процесса. Это один из случаев, когда математическая форма анализа не навязывается экономике извне, а прямо следует из фактических данных. При этом очевидна не только теоретическая, но и практическая значимость подобной модели, если ее удастся построить. Представим, к примеру, как радикально изменится деятельность биржевых аналитиков, если они смогут надежно прогнозировать количественные параметры развития наиболее динамичных фирм.

Приводимые ниже соображения не претендуют на решение столь амбициозной задачи, но лишь намечают возможный путь движения в данном направлении. Исходным пунктом, вероятно, целесообразно взять биологические модели популяционной динамики. В частности, рост численности популяции при неограниченных ресурсах (те самые кролики в Австралии) описывается уравнением, имеющим экспоненциальное решение

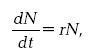(6.1)

где N – число особей; t – время;

r – естественный темп размножения.

С учетом ограниченности ресурсов и возникающей вследствие этого внутривидовой конкуренции экспоненциальное уравнение (6.1) заменяется логистической кривой 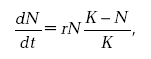(6.2)

(6.2)

где К – предельное число особей, существование которых возможно при данных объемах ресурсов.

Легко видеть, что, пока N << К, дробь в правой стороне формулы (6.2) близка к единице, т. е. при малом (относительно объема ресурсов) числе особей данная формула вырождается в формулу (6.1). Соответственно, развитие популяции, как и в первом случае, идет по экспоненте. Однако при приближении реального числа особей N к предельно возможному числу К дробь стремится к нулю, т. е. рост прекращается. Экспонента выходит на плато, собственно, и превращаясь в логистическую кривую.

Эти простейшие построения в дальнейшем были обобщены с учетом существования межвидовой конкуренции, что было проделано в знаменитой модели Лотки-Вольтерры (Lotka, 1925; Volterra, 1926). Для случая конкуренции двух видов она складывается из двух уравнений

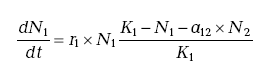(6.3)

и

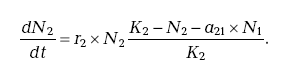(6.4)

Индексы при переменных отражают их принадлежность к первому или второму виду, а коэффициенты а₁₂ и а₂₁ называются коэффициентами конкуренции и отражают в первом случае силу конкурентного давления каждой особи второго вида на первый, а во втором случае, наоборот, особи первого вида на второй.

Рост популяции каждого из видов в модели Лотки-Вольтерры замедляется по мере нарастания численности как исследуемого, так и конкурирующего с ним видов (нехватку травы может вызвать нетолько размножение самих кроликов, но и увеличение численности коз). Поскольку, однако, коэффициенты a₁₂ и a₂₁ могут различаться, то при разных комбинациях их величин конкуренция приводит к качественно разным результатам: вытеснению первого вида вторым, второго вида первым или к различным режимам их сосуществования. Собственно, возможность количественно оценивать условия реализации принципиальных исходов конкурентной борьбы и обеспечила огромный авторитет модели Лотки-Вольтерры в науке.

Представляется, что модель Лотки-Вольтерры естественным образом подходит для моделирования развития «быстрых» фирм, поскольку (6.1) исходно приспособлена для описания экспоненциального роста, (6.2) объясняет процесс его затухания, (6.3) и (6.4) имеют простой механизм учета влияния других претендентов на ресурсы. Вместе с тем необходима содержательная интерпретация данной модели применительно к экономике, а также ее серьезная модификация с целью учета тех реалий, которые в биологии не встречаются.

Прежде всего, представляется, что в качестве ресурсов в микроэкономической версии модели должен фигурировать спрос. Не отрицая значимости материальных ресурсов, следует помнить, что рыночная экономика относится к типу спросоограниченных экономических систем. Само устройство рынка таково, что, имея деньги, в обычном случае (исключения, разумеется, есть) можно приобрести любые материальные ресурсы. Источником же денежных средств для компаний является спрос на их продукцию.

Далее, модель корректно применить к отдельной фирме, а не ко всей «популяции» фирм отрасли. Это в биологии один кролик не может так разрастись по размерам, что индивидуальное поедание им травы постепенно станет сопоставимым с общим объемом данного ресурса. Фирма же в состоянии собственным производством покрыть заметную часть спроса или даже весь совокупный спрос.

Таким образом, N разумно интерпретировать как объем реализации отдельной фирмы. Соответственно, параметр К в этом случае понимается как размер спроса на ее продукцию. Замедление роста «быстрой» фирмы (сход с экспоненты) в этом случае вполне непринужденно объясняется тем, что ее объем производства наткнулся на границы спроса.

Очень важно и содержательное истолкование параметра г, определяющего скорость роста фирмы, крутизну ее экспоненты. Обратим внимание на то, что он не зависит от размеров спроса. Даже если спрос многократно превышает объем предложения, фирма не может расти сколь угодно быстро. Неизбежно возникнут трудности со вводом в строй производственных мощностей, подбором кадров и т. п. Представляется, что в экономике г отражает предельно возможный темп расширения производственного потенциала фирмы.

Мы выходим, таким образом, на экономически внятное объяснение наиболее шокирующего исследователей факта: идеального совпадения динамики реальных цифр реализации продукции многими «быстрыми» фирмами с математически точной экспонентой (напомним, как мы установили, коэффициент качества аппроксимации достигает порой R² = 0,999). Здравый смысл экономиста просто не желает мириться с тем, что объем реализации, т. е. величина, зависящая от множества факторов (автономных колебаний спроса, динамики цен, действий конкурентов, рекламной активности и так далее, и так далее), без малейших отклонений подчиняется простому математическому правилу. Невольно хочется воскликнуть: так не бывает!

Между тем большинство факторов, обычно влияющих на объем реализации, в данном случае просто не являются лимитирующими. Напомним, спрос на экспоненциальном участке роста неограничен (N << К), он «переваривает» любое увеличение предложения. Компания просто в состоянии продать все, что сможет произвести. Соответственно, и скорость роста продаж зависит от единственного фактора – от того предельного темпа, с которым фирма способна расширять свои мощности. Скажем, банк без снижения качества персонала и потери управляемости способен ежегодно осуществлять увеличение численности своих сотрудников не более, чем на 70 %. Если производительность сотрудников не меняется, то и ежегодный прирост объема предлагаемых услуг составит примерно 70 %, что и выражается точной экспонентой.

Что касается дополнительных эффектов, которые возможны в экономике, но не в биологии, то следует, во-первых, учитывать возможность фирмы влиять на объем спроса на свою продукцию. Это бактерия никакими усилиями не может увеличить запас питательного бульона в чашке Петри, а компания способна подстегивать спрос за счет улучшения качества, усиления рекламы, расширения территории сбыта и т. п. 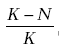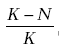Поэтому кроме «изъятий» в дроби , показывающей приближение выпуска продукции к пределу спроса, должны быть учтены и «добавки» к этому максимальному размеру спроса, которые своими действиями может индуцировать сама фирма.

То же самое можно сказать и об описанных выше синергетических эффектах внутри кластеров фирм. Взаимодействие быстрорастущих фирм увеличивает спрос на продукцию каждой из них и, следовательно, поддерживает их рост, поскольку увеличивает притягательность для потребителя всего комплекса товаров и услуг, производством разных компонентов которого они заняты.

Очевидно, что в этих условиях полный потенциал спроса (обозначим его М) уже не будет сводиться к первоначальному максимальному размеру К, но расширится на два названных компонента, т. е.:

М = K + А + B, (6.5)

где А – положительное воздействие фирмы на объем спроса;

В – положительное воздействие синергии с другими фирмами;

М – полный потенциал спроса.

Именно М должен в дальнейшем фигурировать вместо К в уравнениях модели Лотки-Вольтерры.

С другой стороны, на потенциальный спрос, предъявляемый на продукцию данной фирмы, может претендовать и аналогичная продукция конкурентов, что явится, естественно, вычетом из его объема, «достающегося» данной компании. И вычет этот, если учесть описанный выше эффект подражания, может нарастать самым стремительным образом.

В целом принципиальный вид уравнения, описывающего темпы роста каждой из фирм, преобразуется в

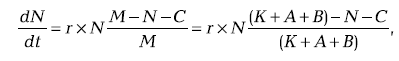(6.6)

где

С – отрицательное воздействие конкурентов на объем спроса.

Переменная А очевидным образом положительно связана с «мощью» фирмы и, следовательно, с объемом реализации N. Чем крупнее фирма, тем больше у нее возможностей с помощью рекламы, стимулирования сбыта и т. п. способствовать росту спроса на свою продукцию. Переменная В, вероятно, окажется разной для разных участников кластера. Логично ожидать формирование ядра кластера из фирм, на которых сконцентрируется наибольшая часть положительных синергетических эффектов, и для которых в силу этого естественно прогнозировать повышенную длительность периода экспоненциального роста. Наконец, переменная С, как и в модели Лотки-Вольтерры, не обязательно окажется симметричной для разных участников конкурентной борьбы. Кто-то будет страдать от конкурентов в большей степени, кто-то в меньшей.

Интересно, что, несмотря на свою простоту, уравнение (6.6) хорошо описывает многие известные рыночные ситуации. А именно, значение переменных:

✓ А = В = 0 описывает случай «Me too»-продуктов;

✓ А > 0, В = 0 типично для фирм, добивающихся успехов маркетинговыми средствами в отсутствие заметных синергетических эффектов;

✓ В > 0 отражает ситуацию синергетического роста целого кластера фирм;

✓ В = f(N₁, N₂) > 0 возникает при так называемых «сетевых эффектах».

Так, при А = В = 0 экспоненциальный рост может выдохнуться, почти не начавшись. Именно это часто происходит, когда фирма находит перспективную нишу, но оказывается неспособной позиционировать в ней свой продукт как уникальный. Из-за высокой прибыльности у новатора оказывается много подражателей (величина С быстро растет), и его рыночная доля стремительно сокращается. Противодействовать же этому, скажем, за счет интенсификации рекламы (повышающей величину А) новатор не может, так как его товар воспринимается как «близнец» конкурирующих с ним изделий. Реклама пойдет на пользу не столько собственному товару, сколько всей товарной категории, т. е. фирма безвозмездно проплатит продвижение конкурирующих продуктов.

Не с этим ли явлением мы имели дело главе 3, когда рассматривали плачевные последствия копирования отечественными фирмами («Акрихином» и др.) новейших иностранных препаратов? Все затраты на вывод на рынок «первого российского дженерика» нес новатор, а плоды успеха вкушали подражатели. И не случайно: как рекламировать собственный пирацетам, когда точно так же называющихся препаратов других фирм не менее 20 штук?

Стоит, напротив, фирме озаботиться формированием бренда, и товар психологически выделится на фоне чужих клонов. Это откроет дорогу к подстегиванию спроса на него (А > 0), и новатор сможет пожать плоды своей первопроходческой деятельности. Вспомним ситуацию с кондитерской фабрикой «Ударница», которая почти проиграла битву с производителями более дешевых (и, обычно, менее качественных) зефира и пастилы, но в последний момент спасла положение, сделав ставку на создание бренда «Шармэль». И все же возможности этого пути продления экспоненциального роста не безграничны: фирма подстегивает расширение рынка, но сама же и заполняет его выпускаемыми товарами. Рано или поздно закон убывающей отдачи снизит эффективность дальнейшего наращивания рекламы, и рост замедлится.

Иным оказывается экономический смысл ситуации, когда опережающими темпами растет переменная В – положительное воздействие синергии с другими фирмами. Ведь в этом случае возникает устойчивая положительная обратная связь роста участников кластера. Фирма n растет быстро потому, что рынок сбыта ее продукции расширяется благодаря выпуску сопутствующих изделий фирмой m. А та, в свою очередь, постоянно ускоряет свое развитие, профитируя от успехов первой фирмы. Как уже отмечалось, это наиболее правдоподобное объяснение фаномена «экономического чуда».

Возможно с помощью уравнения (6.6) описание даже таких экономических «диковинок», как сетевые эффекты. Известно, например, что спрос на интернет-услуги растет по мере роста числа пользователей, поскольку общепринятость этого средства коммуникаций повышает пользу, которую человек извлекает от подключения к сети. Для описания подобных эффектов достаточно допустить, что синергетический эффект зависит от выпущенного всеми конкурентами числа товаров, т. е. В = f(N₁, N₂).

Если учесть, что все перечисленные варианты наблюдаются в экономике одновременно, то становится очевидным, что, в отличие от принципиальной формулы, реальная система уравнений, описывающая процессы внутри кластера, неизбежно окажется достаточно сложной. В настоящее время не вполне ясно и то, как осуществить количественную оценку переменных А, В и С. Представляется, однако, что перечисленные трудности в принципе преодолимы, а задача, как в интеллектуальном, так и в прагматическом отношении, столь привлекательна, что оправдывает усилия.