ГЛАВА XVII: Чёрч, Тюринг, Тарский и другие
Формальные и неформальные системы
НАСТАЛ МОМЕНТ, когда мы уже можем сформулировать один из основных тезисов этой книги любой аспект мышления можно рассматривать как описание на высшем уровне некой системы, которая на низшем уровне управляется простыми и даже формальными правилами. Под «системой» здесь, разумеется, имеется в виду мозг — если не упоминать мыслительные процессы, протекающие в другой среде, такой, скажем, как электрические цепи компьютера. Это создает образ формальной системы, лежащей в основе «неформальной системы» — такой, которая сочиняет каламбуры, находит численные закономерности, забывает имена, «зевает» фигуры в шахматной партии и так далее. То, что мы видим снаружи, — это ее неформальный, явный уровень, уровень программ. С другой стороны, в системе есть также формальный, скрытый уровень (или «субстрат»), уровень аппаратуры — удивительно сложный механизм, переходящий от одного состояния к другому по определенным, физически встроенным в него правилам, согласно поступающим извне сигналам (входным данным).
Нет нужды говорить, что такой взгляд на мозг имеет множество философских и других следствий. Некоторые из них я попытаюсь описать в этой главе. Среди прочего, из этого взгляда, как кажется, следует то, что в своей основе мозг является неким «математическим» объектом. На самом деле, это, в лучшем случае, довольно неуклюжая модель мозга. Дело в том, что даже если в техническом и абстрактном смысле мозг и представляет собой некий тип формальной системы, математики работают с системами простыми и элегантными, в которых все четко определено. Мозгу же, с его десятью миллиардами частично независимых нейронов, соединенных почти случайным образом, далеко до такой ясности, так что он никогда не станет объектом изучения математиков. Если определить «математику» как нечто, чем математикам нравится заниматься, то приходится признать, что свойства мозга — не математические.
Единственный способ понять такую сложную систему как мозг — это использовать блочную картину на все более высоких уровнях, при этом, разумеется, при каждом следующем шаге приходится жертвовать точностью. На высшем уровне мы получаем «неформальную систему», подчиняющуюся такому количеству сложных правил, что у нас пока не хватает слов для ее описания. Именно это — объект поисков специалистов по Искусственному Интеллекту, поисков, которые весьма отличны от математических изысканий. Однако между ними существует некоторая связь — эксперты по ИИ часто имеют математическое образование, а математики часто интересуются работой собственного мозга. Следующий отрывок из автобиографической книги Станислава Улама «Приключения математика» (Stamslaw Ulam, «Adventures of a Mathematician») иллюстрирует этот факт:
Мне кажется, что можно лучше выявить … природу ассоциаций, используя для экспериментов компьютеры. Такое исследование включало бы подразделение на понятия, символы, классы символов, классы классов и так далее, так же, как это делается при исследовании сложных математических или физических систем.
В нашем мышлении должен быть некий метод, некая рекурсивная формула. Группа нейронов начинает работать автоматически, иногда даже без внешнего импульса. Результатом этого повторяющегося процесса является растущая область возбужденных нейронов, которая передвигается по мозгу в зависимости от памяти или чего-то подобного.
Интуиция и Магическая Мистификация Краба
Искусственный интеллект для краткости часто называют ИИ. Мне кажется, что сокращение ИИ могло бы также обозначать Искусственную Интуицию. Цель ИИ — понять, что происходит, когда в мозгу из мириад возможностей делается бесшумный и невидимый выбор той единственной, которая кажется наиболее подходящей в данной сложной ситуации. Во многих жизненных ситуациях дедуктивные рассуждения не годятся — не потому, что они привели бы к неправильным ответам, но потому, что существует огромное множество истинных, но неважных для данной ситуации суждений; приходится принимать в расчет слишком много факторов, и потому логические рассуждения оказываются неэффективными. Взгляните на этот мини-диалог:
— На днях я прочитал в газете, что…
— О, вы прочитали? Из этого следует, что у вас есть глаза. Или, по крайней мере, один глаз. Или, скорее, что у вас в тот момент был по крайней мере один глаз.
Здесь необходимо понимание того, что важно и что неважно; с этим связано чувство простоты и красоты. Откуда берутся эти интуитивные понятия? Каким образом они могут родиться из формальной системы мозга? В Диалоге «Магнификраб» мы встречаемся с некими необычными свойствами Крабьего мозга. По его словам, он просто слушает музыку и отличает красивые мелодии от некрасивых. (По-видимому, для него существует четкая граница.) Ахилл, однако, находит другой способ описания Крабьих способностей: Краб подразделяет суждения теории чисел на истинные и ложные. Но Краб утверждает, что если он это и делает, то только случайно, поскольку он в математике профан. Ахилл более всего удивлен тем, что Краб, как кажется, прямо нарушает знаменитую теорему метаматематики:
ТЕОРЕМА ЧЁРЧА: Не существует универсального метода, позволяющего отличать теоремы ТТЧ от не-теорем.
Это утверждение было доказано в 1936 году американским логиком Алонзо Чёрчем, оно находится в тесной связи с тем, что я называю:
ТЕОРЕМОЙ ТАРСКОГО-ЧЁРЧА-ТЮРИНГА: Не существует универсального метода, позволяющего отличать истинные суждения теории чисел от ложных.
Тезис Чёрча-Тюринга
Чтобы лучше понять Теорему Чёрча и Теорему Тарского-Чёрча-Тюринга, рассмотрим сначала одну из идей, на которых они основаны, — Тезис Чёрча-Тюринга (часто называемый «Тезисом Черча») Это, безусловно, одно из важнейших понятий в философии математики, мозга и мышления.
Этот Тезис напоминает чай тем, что его можно сделать разных степеней крепости. Я изложу здесь различные версии и мы увидим, что из них вытекает.
Первая версия звучит весьма невинно и, пожалуй, даже бессмысленно:
ТЕЗИС ЧЁРЧА-ТЮРИНГА, ТАВТОЛОГИЧЕСКАЯ ВЕРСИЯ: Математические задачи можно решать только математическими методами.
Разумеется, смысл этого утверждения может быть выведен из смысла составляющих его частей. Под «математической задачей» я имею в виду определение того, обладает ли данное число неким арифметическим свойством. Оказывается, что при помощи Геделевой нумерации и родственных ей приемов кодификации, почти любую проблему в любой области математики можно представить в этой форме, таким образом, выражение «математическая задача» сохраняет свое обычное значение. А как насчет «математических методов»? Пытаясь решить, обладает ли некое число определенными свойствами, мы используем лишь ограниченное число операций, комбинирующихся друг с другом сложение, умножение определение равенства или неравенства. Кажется, что циклы, состоящие из этих операций, — единственный инструмент, позволяющий нам заглянуть в мир чисел. Заметьте, что я сказал «кажется». Это слово — основное в Тезисе Черча-Тюринга. Ниже — другая версия этого Тезиса:
ТЕЗИС ЧЁРЧА-ТЮРИНГА, СТАНДАРТНАЯ ВЕРСИЯ: Предположим, что существует метод при помощи которого разумное существо может разделять числа на два класса. Предположим также, что этот метод всегда приводит к ответу за конечный отрезок времени, и что этот ответ — всегда один и тот же для одного и того же числа. В таком случае существует некая конечная программа на Флупе (то есть, некая общерекурсивная функция), которая будет давать точно такие же ответы, как и разумное существо.
Основная идея здесь состоит в том, что любой мыслительный процесс, делящий числа на две категории, может быть описан в форме программы на Флупе. Интуиция утверждает, что других методов, чем имеющиеся во Флупе, не существует, и что невозможно использовать эти методы иначе, чем путем бесчисленных повторений (которые Флуп допускает). Тезис Черча-Тюринга невозможно доказать как Теорему математики — это всего лишь гипотеза о процессах протекающих в человеческом мозгу.
Версия Коллективных Процессов
Некоторые люди могут подумать, что предыдущая версия утверждает слишком много. Такие люди могли бы сформулировать свои возражения следующим образом: «Может существовать некто, подобный Крабу, — некто с почти мистической математической интуицией, кто при этом не умеет объяснить своих удивительных способностей. Возможно, что в мозгу такого человека происходят процессы, непредставимые на Флупе.» Идея заключается в том, что, возможно в нас заложен подсознательный потенциал для совершения вещей, превосходящих сознательные процессы — и это невозможно выразить с помощью элементарных операций Флупа. Для тех, кто выдвигает подобные возражения, мы сформулируем более слабую версию Тезиса, различающую индивидуальные и коллективные мыслительные процессы:
ТЕЗИС ЧЁРЧА-ТЮРИНГА, ВЕРСИЯ КОЛЛЕКТИВНЫХ ПРОЦЕССОВ: Предположим, что существует метод, при помощи которого разумное существо может разделять числа на два класса. Предположим также, что этот метод всегда приводит к ответу за конечный отрезок времени и что этот ответ — всегда один и тот же для одного и того же числа. Если этот метод может быть эффективно сообщен одним разумным существом другому при помощи языка, то в таком случае существует некая конечная программа на Флупе (то есть, некая общерекурсивная функция), которая будет давать точно такие же ответы, как и разумное существо.
Эта версия утверждает, что коллективные методы подвержены «Флупификации», но обходит молчанием индивидуальные методы. Она не говорит, что их невозможно «Флупифицировать», но, по крайней мере, оставляет эту возможность открытой.
Шриниваса Рамануян
Как доказательство против более сильных версий Тезиса Чёрча-Тюринга давайте рассмотрим случай знаменитого индийского математика первой четверти двадцатого века, Шринивасы Рамануяна 1887-1920). Рамануян (рис. 105) родился на юге Индии, в Тамилнаду; он немного изучал математику в старших классах школы. Однажды кто-то, заметив способности мальчика к математике, подарил ему слегка устаревший учебник по математическому анализу, который Шриниваса немедленно проглотил (разумеется, не в буквальном смысле!). После этого Рамануян начал собственные исследования в этой области, и к тому времени, когда ему исполнилось двадцать три года, у него на счету было несколько открытий, которые казались ему важными. Он не знал, к кому обратиться, но однажды он услышал о некоем профессоре математики по имени Г. X. Харди, живущем в далекой Англии. Рамануян записал свои лучшие результаты и послал эту пачку листков ничего не подозревавшему Харди вместе с письмом, которое друзья помогли ему написать по-английски.
Ниже следуют некоторые отрывки, описывающие реакцию Харди, когда он получил эту «посылку»:
Вскоре мне стало ясно, что Рамануян знал гораздо более общие теоремы, но держал их в рукаве… [Некоторые формулы] меня совершенно поразили — я никогда не видел ничего подобного. Одного взгляда на них достаточно, чтобы понять, что они написаны математиком высшего класса. Они, скорее всего, истинны, поскольку никто не может обладать достаточным воображением, чтобы высосать из пальца нечто подобное. Наконец,… автор письма был, по-видимому, абсолютно честен, поскольку гениальные математики встречаются чаще, чем шарлатаны, обладающие таким невероятным талантом.
Результатом этой переписки был приезд Рамануяна в Англию в 1913 году по приглашению Харди и начало тесного сотрудничества между ними, которое было прервано преждевременной смертью Рамануяна от туберкулеза в возрасте тридцати трех лет.
Среди прочего, Рамануян отличался от большинства математиков тем, что его доказательствам не хватало строгости. Иногда он просто называл результат, полученный, по его словам, чисто интуитивно, без какого бы то ни было сознательного поиска. Часто Рамануян говорил, что богиня Намагири сообщила ему ответ во сне. Это повторялось снова и снова, и самое удивительное — даже мистическое — заключалось в том, что многие из его «интуитивных теорем» оказывались ложными! В связи с этим интересен парадокс, заключающийся в том, что иногда событие, которое, как кажется, должно было бы добавить доверчивым людям немного скептицизма, в действительности вызывает обратный эффект. Оно затрагивает эти доверчивые души, соблазняя их намеками на некие удивительные, иррациональные свойства человеческой природы. Именно это произошло с ошибками Рамануяна; многие образованные люди, жаждущие поверить в чудеса, увидели в интуитивных способностях Рамануяна доказательство его мистического прозрения и знания Истины — и его ошибки только усилили их веру.
Возможно, что этому способствовал тот факт, что Рамануян происходил из самой отсталой части Индии, где факиризм и подобные мистические индийские ритуалы практиковались тысячелетиями — и продолжали встречаться во времена Рамануяна, возможно, чаще, чем высшая математика. И его ошибки, вместо того, чтобы подтвердить, что он — всего лишь человек, парадоксальным образом породили веру в то, что заблуждения Рамануяна на самом деле являлись «правотой высшего порядка», некой «восточной истиной», недоступной западному уму. Какая замечательная, почти неотразимая мысль! Даже Харди, кто должен был бы первым опровергнуть идею о мистических способностях Рамануяна, однажды написал: «И все же я не уверен, что, каким-то образом, его промах не является более замечательным, чем любой из его успехов».
Другой выдающейся чертой Рамануяна была его «дружба с целыми числами», по выражению его коллеги Литтлвуда. Многие математики до какой-то степени разделяют эту черту, но у Рамануяна она была развита до крайности. Об этой его характеристике ходили легенды. Одна из них была рассказана Харди:
Однажды я пришел навестить его, когда он лежал больной в Путни. Я сказал ему, что приехал на такси с номерным знаком 1729 и заметил, что в этом номере нет ничего интересного и что как бы это не оказалось дурным предзнаменованием. «Напротив», — ответил он, — «это очень интересный номер: это наименьшее, число, которое можно выразить как сумму двух кубов двумя разными способами». Я, естественно, спросил его, знает ли он ответ на аналогичную задачу для четвертой степени, на что он после минутного раздумья ответил, что он точно не знает, но что ему кажется, что это будет очень большое число.
Ответом на эту задачу оказывается:
635 318 657 = 1344 + 1334 = 1584 + 594
Читатель может попробовать решить аналогичную задачу для квадратов, что намного легче.
Интересно подумать, почему Харди сразу перешел к четвертой степени. В конце концов, существуют несколько других естественных обобщений уравнения:
u 3 + v 3 = x 3 + у 3
Например, можно подумать о том, как представить некое число в виде суммы двух кубов тремя различными способами:
r 3 + s 3 = u 3 + v 3 = x 3 + у 3
или использовать три различных куба:
u 3 + v 3 + w 3 = x 3 + у 3 + z 3
r 4 + s 4 + t 4 = u 4 + v 4 + w 4 = x 4 + у 4 + z 4
Однако в каком-то смысле задача Харди оказывается наиболее «математической». Возможно ли будет когда-либо запрограммировать это чувство математической эстетики?
Другой рассказ о Рамануяне взят из его биографии, написанной его соотечественником С. Р. Ранганатаном. Этот рассказ носит название «Прозрение Рамануяна» и принадлежит его товарищу по Кембриджскому университету, П. С. Махаланобису, также выходцу из Индии:
Однажды я пришел к нему в комнату, чтобы пообедать вместе. Дело было некоторое время спустя после начала Первой мировой войны. В руках у меня был экземпляр ежемесячника «Странд Магазин», в котором в то время печатались всяческие головоломки для читателей. Рамануян, стоя у плиты, размешивал что-то в кастрюльке. Я сидел у стола, листая журнал; вдруг меня заинтересовала задача об отношении двух чисел. Я забыл подробности и помню только тип задачи. Два британских офицера были расквартированы в Париже в двух различных домах на длинной улице; номера этих домов соотносились определенным образом, и задача заключалась в том, чтобы их найти. На вид проблема казалась нетрудной — пользуясь методом проб и ошибок, я нашел ответ за несколько минут.МАХАЛАНОБИС (шутливо): Вот тут для вас задача.РАМАНУЯН (не переставая мешать): Что за задача?Я прочитал ему задачу.РАМАНУЯН: Записывайте ответ (диктуя непрерывную дробь).Первый член в дроби был равен моему ответу, остальные представляли собой следующие решения. При этом число домов на улице росло до бесконечности.Я был поражен.МАХАЛАНОБИС: Неужели вы решили это сразу?РАМАНУЯН: Разумеется. Как только я услышал задачу, я сразу понял, что ответом должна быть непрерывная дробь; тогда я подумал: «Какая именно?» — и тут же увидел решение. Это было очень просто.
После смерти Рамануяна Харди, как его ближайшего сотрудника, часто спрашивали, не было ли в стиле мышления Рамануяна каких-либо мистических и необычных элементов. Вот один из ответов Харди:
Меня часто спрашивают, не было ли у Рамануяна какого-нибудь особого секрета, не пользовался ли он методами иного типа, отличными от методов других математиков и было ли его мышление действительно необычным. Не могу ответить на эти вопросы с достаточной уверенностью, но лично я в это не верю. Я считаю, что все математики в основном думают примерно одинаково, и что Рамануян не являлся исключением.
Здесь Харди формулирует свою собственную версию Тезиса Чёрча-Тюринга. В перифразе она звучит так:
ТЕЗИС ЧЁРЧА-ТЮРИНГА, ВЕРСИЯ ХАРДИ: На низшем уровне все математики изоморфны.
Это не приравнивает математический потенциал математиков к потенциалу общерекурсивных функций; для этого надо лишь показать, что умственные способности какого-либо одного математика не более общие, чем рекурсивные функции. Тогда, если вы принимаете Версию Харди, то вы должны принять ее для всех математиков. Далее Харди сравнивает Рамануяна с людьми, обладающими удивительной способностью к вычислениям.
Его память и его способности к вычислениям были весьма необычны, но их нельзя было назвать «ненормальными». Если ему нужно было перемножить два больших числа, он делал это обычным способом — правда, с необычной скоростью и аккуратностью — но не быстрее и не аккуратнее, чем любой другой математик, кто от природы быстро соображает и имеет опыт в вычислениях.
Харди описывает то, что казалось ему выдающимися чертами интеллекта Рамануяна:
Кроме памяти, терпения и способности к вычислениям, он обладал такой способностью к обобщениям и к быстрому изменению своих гипотез и таким чувством формы, что в то время ему не было равных в его области.
Те места этого отрывка, которые я выделил курсивом, кажутся мне блестящей характеристикой некоторых наиболее тонких и неуловимых черт разума вообще. Харди заключает, с некоторой грустью:
(В его трудах) не было той простоты и неизбежности, которая отличает величайшие математические открытия; они были бы более великими, если бы они были менее странными. Но зато его работы имели нечто, чего не может отрицать никто — они были глубоко и непобедимо оригинальны. Возможно, что он был бы более великим математиком, если бы его «поймали» и «приручили» в юности; он открыл бы много нового и, без сомнения, более важного. С другой стороны, он был бы менее похож на Рамануяна и более — на европейского профессора, и потеря от этого могла быть больше, чем выигрыш.
По тому, как романтично говорит Харди о Рамануяне, видно, какое уважение он питал к своему индийскому коллеге.

Рис. 105. Шриниваса Рамануян и одна из его странных индийских мелодий.
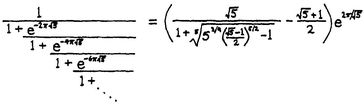
«Гениальные идиоты»
Существует еще один тип людей, чьи математические способности кажутся необъяснимыми с рациональной точки зрения — так называемые «гениальные идиоты», могущие производить сложные расчеты в уме (или где бы там ни было) с быстротой молнии. Иоганн Мартин Захарий Дэйз, живший с 1824 по 1861 и работавший для нескольких европейских правительств, был выдающимся примером. Он не только мог перемножить в уме два стозначных числа, но также имел удивительное чувство количества. Он мог сказать, не считая, сколько овец на поле, сколько слов в предложении и так далее, приблизительно до 30 — в отличие от большинства из нас, имеющих это чувство примерно до 6. При этом Дэйз вовсе не был идиотом…
Я не буду пересказывать здесь множество интересных историй о «людях-калькуляторах», поскольку моя цель иная. Но мне кажется важным опровергнуть мнение, что они совершают свои расчеты при помощи неких таинственных, не поддающихся анализу методов. Хотя часто вычислительные способности таких гениев намного превосходят их способности объяснять свои результаты, иногда среди них появляется человек, наделенный и другими талантами. Из наблюдений таких людей и из работ психологов можно сделать заключение, что в голове людей-калькуляторов не происходит ничего сверхъестественного — просто их мозг совершает промежуточные действия очень быстро и уверенно, подобно умелому атлету, быстро и грациозно делающему сложные упражнения. Свои ответы они получают не благодаря мгновенному озарению (хотя субъективно некоторым из них может казаться именно так), но, как и все мы, при помощи последовательных вычислений — то есть при помощи Флупо- или Блупоподобных действий.
Одним из наиболее очевидных подтверждений того, что не существует никакого мистического «прямого телефона к Богу», является тот факт, что, по мере того как числа становятся больше, ответы становятся медленнее. Если бы ответы исходили от Бога или некоего «оракула», этого бы не происходило. Было бы интересно составить некий график, соотносящий время раздумий «человека-калькулятора» с величиной данных ему чисел и количеством требуемых операций, и вычислить по нему алгоритмы этого процесса.
Изоморфная Версия Тезиса Чёрча-Тюринга
Это вплотную подводит нас к усиленной стандартной версии Тезиса Чёрча-Тюринга:
ТЕЗИС ЧЁРЧА-ТЮРИНГА, ВЕРСИЯ ИЗОМОРФИЗМА: Предположим, что существует метод, при помощи которого разумное существо может разделять числа на два класса. Предположим также, что этот метод всегда приводит к ответу за конечный отрезок времени и что этот ответ — всегда один и тот же для одного и того же числа. Тогда существует некая конечная программа на Флупе (то есть, некая общерекурсивная функция), которая будет давать точно такие же ответы, как и разумное существо. Более того, мыслительный процесс и эта программа Флупа будут изоморфны в том смысле, что на каком-то уровне будет существовать соответствие между операциями выполняемыми компьютером и мозгом.
Заметьте, что здесь не только усилено заключение, но и опущено условие сообщаемости, характеризовавшее более слабую Коллективную Версию. Давайте рассмотрим эту смелую версию Тезиса.
Эта версия утверждает, что когда человеческое существо что-то вычисляет, его умственная деятельность может быть изоморфно отображена в некой программе Флупа. Это не означает, разумеется, что в мозгу действует настоящая программа Флупа, написанная на языке Флуп с командами НАЧАЛО КОНЕЦ ПРЕРВАТЬ и так далее. Это значит только то, что операции выполняются в том же порядке в каком они могли бы выполняться в программе Флупа, и что логическая структура вычислений может быть отображена во Флупе.
Чтобы эта идея имела смысл, мы должны различать уровни как в компьютере, так и в мозгу — иначе эта мысль может показаться совершенной чепухой. Предположительно, операции вычисления в наших головах совершаются на высшем уровне, опирающемся на низшие уровни и, в конечном счете, на «аппаратуру». Таким образом, говоря об изоморфизме, мы подразумеваем, что высший уровень может быть изолирован и что мы можем обсуждать происходящие там процессы независимо от того, что делается на других уровнях — и затем проимитировать этот высший уровень в программе Флупа. Точнее, наше предположение заключается в том что существуют некие блоки мысленной «программы», которые играют роль математических построений и активируются таким образом, который может быть в точности отображен в программе Флупа (см. рис. 106). Эти блоки существуют благодаря инфраструктуре мозга, которую мы обсуждали в главах ХI и XII, а также в «Прелюдии» и в «Муравьиной фуге». Мы не предполагаем изоморфной деятельности на низших уровнях мозга и компьютера (нейроны и биты).
Если не букву, то дух Версии Изоморфизма можно передать, говоря, что гениальный идиот, вычисляя, скажем логарифм π, проделывает операции, изоморфные операциям карманного калькулятора, решающего ту же задачу. Изоморфизм существует на уровне арифметических действий, а не на уровне нейронов мозга и электрических цепей калькулятора. (Разумеется, при решении любой задачи можно следовать различными путями — но, в принципе, если не человек, то карманный калькулятор может быть запрограммирован вычислить ответ каким-то определенным путем.)
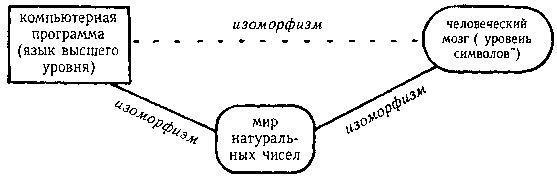
Рис. 106. Поведение натуральных чисел может быть представлено в человеческом мозгу или в компьютерной программе. Эти два представления могут быть затем отображены друг на друга на соответствующем абстрактном уровне.
Представление знаний о мире
Все это кажется убедительным, когда мы говорим о теории чисел, поскольку события там происходят в весьма ограниченном и чистом мире. Его границы, правила и обитатели определены четко, словно в хорошо построенном лабиринте. Такой мир намного менее сложен, чем открытый и неопределенный мир, в котором мы обитаем. Будучи поставлена, задача теории чисел полностью самодостаточна; задача реального мира, напротив, никогда не может быть с уверенностью изолирована от воздействия этого мира. Например, чтобы заменить перегоревшую лампочку, вам может понадобиться подвинуть помойное ведро; при этом вы можете нечаянно толкнуть стоящий поблизости столик и уронить на пол лежавшие на нем таблетки; после чего вам придется подмести пол, чтобы ваша собака их не съела… и так далее, и тому подобное. Таблетки, помойное ведро, собака и электрическая лампочка весьма мало соотносятся между собой, но здесь, благодаря некоему повседневному событию, они оказались в тесной связи. И невозможно предсказать, какие еще предметы оказались бы вовлечены в эти отношения, если бы события немного изменились. С другой стороны, решая задачу теории чисел, вам никогда не придется иметь дело с такими посторонними предметами, как таблетки, собаки, помойные ведра и щетки. (Разумеется, ваше интимное знакомство с означенными предметами может сослужить вам службу, когда вы пытаетесь представить себе задачу в форме геометрических фигур — но это совершенно другое дело.)
Реальный мир так сложен, что трудно вообразить себе маленький карманный калькулятор, который мог бы ответить на ваши вопросы путем нажатия кнопок с надписями «собака», «помойное ведро», «лампочка» и так далее. На самом деле, до сих пор очень трудно заставить даже большой и быстрый компьютер отвечать на вопросы о ситуациях, которые кажутся нам весьма простыми. Кажемся, что для того, чтобы компьютер «понял» задачу, необходимы много знаний и умение соотносить их друг с другом должным образом. Процессы мышления можно сравнить с деревом, чья видимая часть твердо стоит на земле, но, при этом зависит от невидимых корней, протягивающихся далеко под землей, поддерживающих и питающих дерево. В данном случае под корнями понимаются сложные процессы, происходящие на подсознательных уровнях — процессы, результаты которых управляют нашим мышлением, но о которых мы сами не подозреваем. Они работают как «пусковые механизмы символов», которые мы обсуждали в главах XI и XII.
Размышления о реальном мире очень отличаются от того, что происходит, когда мы перемножаем два числа — в последнем случае все находится, так сказать, над землей, открытое для обозрения. В арифметике высший уровень может быть выделен и промоделирован на аппаратуре различных типов: механические складывающие аппараты, карманные калькуляторы, компьютеры, человеческие мозги и так далее. Именно это и утверждает Тезис Чёрча-Тюринга. Но когда дело касается понимания реального мира, то трудно представить себе, что высший уровень возможно выделить и запрограммировать отдельно. Пусковые механизмы символов слишком сложны. Мысль должна «просочиться», профильтроваться сквозь многие уровни. В частности — и это возвращает нас к основным темам глав XI и XII — представление в мозгу реального мира, хотя и основанное до некоторой степени на изоморфизме, включает некоторые элементы, не имеющие никакого соответствия в окружающей нас действительности. Оно гораздо сложнее элементарных мысленных образов «собаки», «щетки» и так далее. Конечно, все эти символы существуют, но их внутренняя структура необыкновенно сложна и почти недоступна сознательному исследованию. Более того, стараться найти соответствие внутренней структуре какого бы то ни было символа в реальном мире было бы напрасным трудом.
Процессы, которые не так легко выделить
Мозг является весьма необычной формальной системой, поскольку на низшем, нейронном уровне там где действуют «правила», меняющие состояние системы, может не существовать интерпретации примитивных элементов (таких как возбуждение отдельных нейронов или, может быть, даже события еще более низкого уровня). Однако, на высшем уровне возникает осмысленная интерпретация — соответствие между крупными «облаками» нейронной активности, которые мы назвали «символами» и событиями реального мира. Это напоминает Геделево построение тем, что в обоих случаях изоморфизм высшего уровня позволяет наделять строчки смыслом более высокого уровня, однако в Геделевом построении значение высшего уровня опирается на значение низших уровней — то есть оно выводится из значения низших уровней при помощи Геделевой нумерации. С другой стороны, события, происходящие в мозгу на нейронном уровне не имеют соответствующей интерпретации в реальном мире — они совершенно ничего не имитируют Они являются всего лишь субстратом, поддерживающим высший уровень, подобно тому, как транзисторы в карманном калькуляторе поддерживают его числовую деятельность Из этого следует что невозможно выделив высший уровень в чистом виде, создать изоморфную копию программы если мы хотим отобразить мозговые процессы, участвующие в понимании реального мира, нам придется отобразить также и некоторые процессы происходящие на низшем уровне, — так сказать, «языки мозга». Может оказаться, что при этом нам придется спуститься до уровня самой «аппаратуры».
В процессе создания программы с целью добиться «разумного» (то есть человекоподобного) внутреннего представления об окружающей действительности в какой-то момент приходится использовать структуры и процессы, не допускающие прямолинейной интерпретации — иными словами, не имеющие прямого соответствия в реальном мире. Эти низшие уровни программы могут быть поняты не благодаря их прямой связи со внешним миром а благодаря их каталитическому воздействию на лежащие над ними уровни. (Конкретное воплощение этой идеи было предложено Муравьедом в «Муравьиной фуге»: неописуемо скучный кошмар прочтения книги на низшем уровне.)
Лично мне кажется, что такая многоуровневая структура концептуальных систем становится необходимой в тот момент, когда процессы, включающие образы и аналогии становятся значимыми элементами программы — в отличие от процессов которые управляют дедуктивными рассуждениями. Процессы, управляющие дедуктивными рассуждениями могут быть запрограммированы на практически единственном уровне и таким образом являются выделимыми по определению. Согласно моей гипотезе, мыслительные процессы, использующие воображение и аналогию изначально требуют нескольких уровней субстрата и следовательно являются невыделимыми. Кроме того, я считаю что именно в этот момент начинают возникать способности к творчеству — из чего вытекает что эти способности изначально зависят от неких «неинтерпретируемых» процессов низшего уровня. Разумеется, весьма интересно выяснить, на что опирается творческое мышление; в следующих двух главах мы обсудим некоторые существующие на этот счет гипотезы.
Символы редукционистской веры
Одним из способов представлять отношения между высшими и низшими уровнями мозга является следующий. Возможно построить такую нейронную сеть, которая на местном уровне (то есть на уровне отдельных нейронов) работала бы точно так же, как нейронная сеть мозга, но в которой не возникало бы никакого значения на высшем уровне. То, что низший уровень состоит из взаимодействующих нейронов, еще не гарантирует появления значения на высшем уровне, подобно тому, как наличие макаронных буковок в алфавитном супе не гарантирует того, что в тарелке будут плавать слова и предложения. Значение высшего уровня — это факультативная черта нейронных сетей, которая может возникнуть в процессе эволюции, как результат воздействия окружающей среды.
Диаграмма на рис. 107 иллюстрирует тот факт, что рождение значения на высшем уровне необязательно. Стрелка, указывающая наверх, означает, что может существовать субстрат, не имеющий высшего значения, — но не наоборот: высшие уровни должны опираться на низшие уровни.
Эта диаграмма подразумевает возможность компьютерной симуляции нейронных сетей. В принципе такое возможно, как бы сложны ни были эти сети, если возможно описать поведение отдельных нейронов в терминах операций, выполнимых на компьютере. Это важное утверждение, которое почти никем не ставится под сомнение. Тем не менее, это является одним из символов «редукционистской веры», нечто вроде «микроскопической версии» тезиса Чёрча-Тюринга. Ниже эта версия сформулирована целиком:
ТЕЗИС ЧЁРЧА-ТЮРИНГА, МИКРОСКОПИЧЕСКАЯ ВЕРСИЯ: Поведение отдельных компонентов человеческого существа может быть симулировано на компьютере. Следовательно, поведение отдельных компонентов (обычно ими считаются клетки) может быть вычислено на Флупе (общерекурсивная функция) с любой степенью аккуратности, если дано достаточно точное описание как внутреннего состояния данного компонента, так и его окружения.
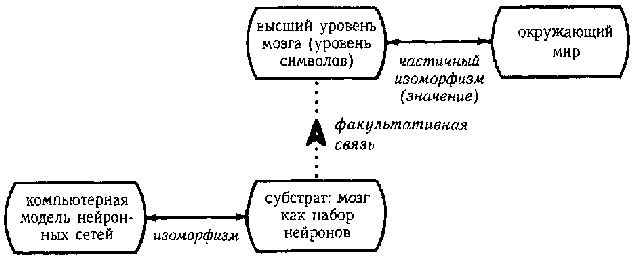
Рис. 107. Нейронная и символическая деятельность мозга.
Эта версия Тезиса утверждает, что процесс мышления, хотя он и имеет больше уровней организации, не более загадочен, чем, скажем, процесс пищеварения. В наше время никто не осмелился бы выдвинуть предположение, что люди переваривают пищу не благодаря обыкновенным химическим процессам, а благодаря некой магической и мистической «ассимиляции». Эта версия Тезиса Ч-Т просто применяет те же рассуждения к мышлению. Короче, в ней высказывается предположение, что мозговые процессы, в принципе, возможно понять. Поэтому я и назвал это мнение символом редукционистской веры.
Ниже дано резюме Микроскопического Тезиса Ч-Т в этом новом, макроскопическом виде:
ТЕЗИС ЧЁРЧА-ТЮРИНГА, РЕДУКЦИОНИСТСКАЯ ВЕРСИЯ Все процессы, происходящие в мозгу, опираются на субстрат, поддающийся вычислению.
Это утверждение является, пожалуй, сильнейшей теоретической поддержкой для возможности создания Искусственного Интеллекта. Разумеется, целью исследований по Искусственному Интеллекту не является симуляция нейронных сетей, поскольку эти исследования основаны на другой вере, что важные характеристики интеллекта могут опираться на иные, чем органический мозг, субстраты. На рис. 108 показаны предполагаемые отношения между Искусственным Интеллектом, естественным разумом и реальным миром.
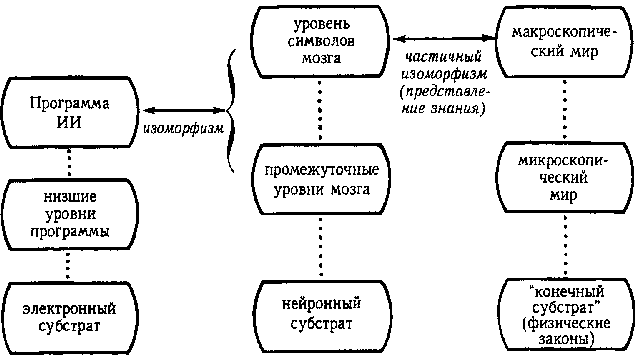
Рис. 108. Центральным понятием в исследованиях по Искусственному Интеллекту является то, что уровень символов мозга может быть «выделен» из их нейронного субстрата и пересажен в другую среду, такую, например, как электронные цепи компьютера. Пока неясно, насколько глубоко должен зайти этот процесс имитации мозга.
Параллельный прогресс в ИИ и симуляции мозга?
В настоящее время предположение, что для достижения ИИ придется проимитировать всю аппаратуру мозга, звучит ужасно для большинства специалистов по ИИ. И тем не менее, возникает вопрос: «Насколько точно необходимо скопировать мозг, чтобы получить ИИ?» Ответ, скорее всего, зависит от того, какие человеческие характеристики мы хотим имитировать.
Является ли умение хорошо играть в шашки показателем интеллекта? Если так, то ИИ уже существует, поскольку шашечные программы могут соревноваться на равных с игроками мирового класса. Или интеллектом является умение символически интегрировать функции, чем занимаются первокурсники на математическом факультете? В таком случае, ИИ уже существует, поскольку программы символического интегрирования делают это лучше, чем люди. Или же на интеллект указывает умение хорошо играть в шахматы? В этом случае, ИИ быстро прогрессирует, поскольку шахматные программы уже выигрывают у большинства сильных любителей, и уровень компьютерных шахмат, скорее всего, будет постепенно улучшаться.
История показывает, что в прошлом люди весьма приблизительно представляли себе, какими качествами должен обладать механизм, чтобы его можно было признать разумным. Иногда кажется, что каждый новый шаг на пути создания ИИ, вместо того, чтобы произвести нечто такое, что все признали бы разумным, углубляет наше понимание того, что интеллектом не является. Если разум включает возможность познания, творческие способности, эмоциональные реакции, чувство красоты, самосознание, то специалистам по ИИ еще предстоит долгий путь — и, возможно, что эти черты удастся воспроизвести, только целиком симулировав человеческий мозг.
Красота, Краб и душа
Имеет ли все это какое-либо отношение к Крабьему музицированию перед Ахиллом? Здесь затронуты два вопроса, а именно:
(1) Может ли какой-либо мозговой процесс с абсолютной точностью отличать истинные утверждения ТТЧ от ложных, не нарушая при этом Тезиса Чёрча-Тюринга, или же подобное в принципе невозможно?
(2) Является ли восприятие красоты мозговым процессом?
Прежде всего заметим, в ответ на (1), что, если допустить нарушения Тезиса Чёрча-Тюринга, то, по-видимому, не существует никаких серьёзных препятствий для того, чтобы странные события Диалога стали возможны. Таким образом, мы хотим знать, должен ли человек, верящий в Тезис Чёрча-Тюринга, сомневаться в способностях Краба. Ответ на этот вопрос зависит от того, о какой версии Тезиса Чёрча-Тюринга идет речь. Например, если вы принимаете Коллективную Версию Тезиса, то легко можете согласовать с ней поведение Краба, указав на то, что его способность невозможно выразить словами. С другой стороны, если вы верите в Редукционистскую Версию, вам будет трудно поверить в способности, которыми хвастается Краб (из-за Теоремы Чёрча, которая будет доказана ниже). Вера в промежуточные версии Тезиса позволяет некоторую степень приспособляемости в этом вопросе. Разумеется, меняя свои взгляды в зависимости от обстоятельств, можно добиться еще большей гибкости.
Давайте рассмотрим еще одну версию Тезиса Т-Ч — версию, с которой молчаливо соглашаются многие люди и которая была по-разному изложена разными авторами. К числу самых знаменитых сторонников этой версии принадлежат философы Губерт Дрейфус, С. Жаки, Мортимер Таубе, и Ж. Р. Лукас, биолог и философ Майкл Полани (убежденный холист) и знаменитый австралийский нейрофизиолог Джон Экклз. Я уверен, что многие другие авторы выражали подобные идеи и что многие читатели им симпатизировали. Ниже я попытался суммировать их общие взгляды. Возможно, что мне не совсем удалось воздать должное этим идеям, но я попытался здесь передать их дух так точно, как только мог.
ТЕЗИС ЧЁРЧА-ТЮРИНГА, ВЕРСИЯ ДУШИ: Некоторые происходящие в мозгу процессы могут быть приблизительно воспроизведены на компьютере — но не большинство этих процессов и, безусловно, не самые интересные из них. Но даже если бы удалось симулировать все процессы мозга, то все равно осталось бы объяснить душу, на что не способен никакой компьютер.
Эта версия имеет двойное отношение к ситуации Диалога «Магнификраб». С одной стороны, ее сторонники, скорее всего, нашли бы эту ситуацию глупой и неправдоподобной, но в принципе возможной. С другой стороны, они, возможно, сказали бы, что понимание красоты — это одно из свойств неуловимой души и, следовательно, оно доступно только людям, а не машинам.
Мы еще вернемся к этому, но сначала, раз уж мы заговорили о «душистах», мы должны выразить их версию Тезиса в еще более сильной форме, поскольку именно в нее верит на сегодняшний день множество образованных людей.
ТЕЗИСА ЧЁРЧА-ТЮРИНГА, ВЕРСИЯ ТЕОДОРА РОСЗАКА: Компьютеры просто смешны — как, впрочем, и вся наука.
Подобное мнение преобладает среди тех людей, которые видят угрозу человеческим ценностям во всем, что пахнет числами или точностью. Жаль, что они не видят всей глубины, сложности и красоты исследования таких абстрактных структур, как человеческий мозг — исследования, которое ставит нас лицом к лицу с вопросом о том, что такое человек.
Возвращаясь к красоте — мы собирались ответить, является ли восприятие красоты мозговым процессом и, если так, то можно ли симулировать этот процесс на компьютере. Те, кто не верит, что красота воспринимается мозгом, вряд ли согласятся с тем, что компьютер сможет это сделать. Те же, кто считают, что этот процесс происходит в мозгу, в свою очередь делятся на две группы в зависимости от того, в какую версию Тезиса Черча-Тюринга они верят. Крайний редукционист сказал бы, что любой происходящий в мозгу процесс в принципе может быть трансформирован в компьютерную программу, однако другие могут считать, что красота — слишком неопределенное понятие, чтобы она могла быть выражена в компьютерной программе. Может быть, они думают, что понятие красоты включает элемент иррациональности и поэтому оно несовместимо с самим духом компьютеров.
Иррациональное и рациональное могут сосуществовать на разных уровнях
Мысль о «несовместимости иррационального с самим духом компьютеров» основана на серьёзном смешении уровней. Это ошибочное мнение опирается на идею, что поскольку компьютеры — безошибочно функционирующие машины, они, таким образом, должны быть «логичными» на всех уровнях. Однако совершенно очевидно, что компьютер может быть запрограммирован таким образом, чтобы напечатать серию нелогичных высказываний — или, для разнообразия, несколько высказываний со случайными значениями истинности. И все же, следуя подобным инструкциям, компьютер не совершит никакой ошибки! Наоборот, ошибкой было бы, если бы компьютер выдал что-либо отличное от высказываний, которые ему было приказано напечатать. Это показывает, как безошибочная работа на одном уровне может лежать в основе манипуляций символами на высшем уровне — и цель высшего уровня может быть совершенно отлична от провозглашения истины.
С другой стороны, не следует забывать, что мозг также состоит из безошибочно функционирующих элементов — нейронов. Как только сумма входящих сигналов превышает порог чувствительности нейрона, он возбуждается. Нейрон никогда не забывает своих арифметических познаний, он никогда не ошибается, складывая входящие сигналы. Даже после своей смерти, нейрон продолжает действовать правильно, в том смысле, что его составные части продолжают повиноваться законам математики и физики. Однако мы все прекрасно знаем, что, несмотря на это, нейроны удивительным образом способны порождать ошибочное поведение высшего уровня. На рис. 109 я попытался показать такое столкновение уровней: неверное мнение, существующее на уровне программы, порождено безошибочно функционирующей аппаратурой мозга.
Дело в том, что, как я уже сказал ранее в других контекстах, значение может существовать на двух или более различных уровнях оперирующей символами системы и вместе со значением на каждом из этих уровней может существовать истинность или ложность. Присутствие значения на данном уровне определяется тем, есть ли на этом уровне изоморфное (в какой-либо степени) отображение реальности.
Таким образом, тот факт, что нейроны никогда не ошибаются в сложении (и даже в гораздо более сложных вычислениях) совершенно не влияет на правильность заключений высшего уровня, который опирается на эту аппаратуру. Чем бы не занимался наш высший уровень — попыткой доказать коаны булева буддизма или медитацией над теоремами дзеновой алгебры, — нейроны нашего мозга функционируют рационально. Совершенно так же, символические процессы высшего уровня, порождающие чувство красоты у нас в мозгу, полностью рациональны на безошибочно функционирующем низшем уровне; вся иррациональность, если таковая имеется, принадлежит высшему уровню и является эпифеноменом — следствием событий, происходящих на низшем уровне.
Попытаюсь проиллюстрировать ту же идею в ином контексте: представьте себе, что вы пытаетесь выбрать между тортами «Прага» и «Птичье молоко». Значит ли это, что ваши нейроны тоже колеблются и не могут решить, возбуждаться им или нет? Разумеется, нет. Ваши гастрономические колебания — это состояние высшего уровня, которое полностью зависит от возбуждения тысяч нейронов определенным образом. Это кажется нелепым, но если подумать, становится ясно, что это только естественно. Однако я думаю, что было бы справедливо сказать, что почти вся путаница насчет мозгов и компьютеров происходит именно из-за этого элементарного смешения уровней.
Нет причин полагать, что безошибочное функционирование компьютерной аппаратуры не может породить таких сложных состояний высшего уровня как замешательство, забывчивость или восприятие красоты. Для этого было бы необходимо наличие множества подсистем, взаимодействующих друг с другом согласно сложной «логике». Явным следствием этого было бы логичное или нелогичное поведение, опирающееся на скрытый уровень надежной, безошибочной аппаратуры.

Рис. 109. Мозг рационален, разум может не быть таковым. (Рисунок автора.)
Новые доводы против Лукаса
Этот тип различения между уровнями дает нам новые аргументы в споре с Лукасом. Он основывает свои рассуждения на идее, что Гёделева Теорема по определению приложима к машинам. На самом деле, Лукас делает еще более выразительное заявление:
Теорема. Гёделя должна быть приложима к кибернетическим машинам, поскольку сама суть таких машин — в том, что они являются воплощениями формальных систем.
Как мы видели, это верно на низшем уровне — уровне аппаратуры; но поскольку могут существовать и высшие уровни, это не является последним словом в данном вопросе. Лукас создает впечатление, что в имитирующих разум машинах, которые он обсуждает, имеется только один уровень, где происходит манипуляция символами. Например, Правило Отделения (называемое в его статье «Модус Поненс») было бы встроено в аппаратуру и было бы неизменной чертой подобной машины. Он идет еще дальше и сообщает, что если бы Модус Поненс не был непоколебимым столпом этих машин и его иногда можно было бы обойти, то:
Система перестала бы быть формальной логической системой, и подобная машина с трудом могла бы быть названа моделью разума.
Необходимо учитывать, что многие программы, разрабатываемые специалистами по Искусственному Интеллекту, сильно отличаются от программ с жесткими правилами и наборами аксиом — программ, занятых поисками численно-теоретических истин. И все же они безусловно задуманы как «модели разума». На их высшем — «неформальном» — уровне может идти манипуляция символами, создание аналогий, забывание идей, перепутывание понятий, стирание различий и. т. д. Но это не противоречит тому, что все эта деятельность зависит от безошибочного функционирования лежащей в их основе аппаратуры, так же как мозг зависит от правильного функционирования его нейронов. Так что программы ИИ все еще являются «конкретными воплощениями формальных систем» — но они вовсе не те машины, к которым применимо преобразованное Лукасом доказательство Гёделя. Аргументы Лукаса приложимы только к их низшему уровню — уровню, на котором их интеллект, каким бы он ни был, не находится.
Лукас также показывает свой сверхупрощенный взгляд на то, как возможно представить мыслительные процессы на компьютере, когда он пишет о непротиворечивости:
Если бы мы в действительности являлись противоречивыми машинами, мы были бы довольны собственной противоречивостью и не моргнув глазом утверждали бы обе части противоречивого высказывания. Более того, мы вообще могли бы утверждать все, что угодно — но этого не происходит. Легко показать что в противоречивой формальной системе любое высказывание доказуемо.
Это последнее предложение показывает, что Лукас считает, что Исчисление Высказываний должно быть по необходимости встроено в любую формальную систему, которая способна на рассуждения. В частности, он имеет в виду теорему <<Р Λ ~Р>эQ>. Исчисления Высказываний, явно придерживаясь ошибочного мнения, что это — неотъемлемая черта механизированных рассуждений. Однако вполне вероятно, что процессы логической мысли возникнут как следствие работы программ ИИ, вместо того, чтобы быть предварительно запрограммированными. Это именно то, что происходит с людьми! Нет причин полагать, что Исчисление Высказываний, с его жесткими правилами и довольно глупым определением непротиворечивости, которое из этих правил вытекает, возникнет в результате действия такой программы.
Фундамент ИИ
Теперь мы можем подвести итоги нашему обсуждению различия между уровнями и дать последнюю, наиболее сильную версию Тезиса Черчй-Тюринга.
ТЕЗИС ЧЁРЧА-ТЮРИНГА ВЕРСИЯ ИИ: Любые мыслительные процессы могут быть симулированы при помощи компьютерной программы, написанной на языке, равномощном Флупу (то есть языке, на котором возможно запрограммировать все частично-рекурсивные функции).
Нужно заметить, что на практике многие специалисты по ИИ верят в идею, родственную тезису Ч-Т, я называю ее Тезисом ИИ.
ТЕЗИС ИИ: По мере того, как машинный разум прогрессирует, механизм, на котором он основан, постепенно становится все ближе к механизму, на котором основан человеческий разум. Иными словами, любой разум — лишь вариация одной и той же темы, чтобы создать настоящий разум, работники ИИ должны подойти как можно ближе к низшим уровням, к механизмам мозга, если они хотят, чтобы машины обладали теми же возможностями, что и мы.
Теорема Чёрча
Вернемся к Крабу и к вопросу о том, совместима ли с реальностью его разрешающая процедура, устанавливающая теоремность (представленная в виде фильтра музыкальной красоты). На самом деле, из событий Диалога мы не можем с уверенностью заключить, является ли дар Краба способностью отличать теоремы от не-теорем, или же способностью отличать истинные высказывания от ложных. Разумеется, во многих случаях это одно и то же, но Теорема Геделя показывает, что так бывает не всегда. Однако это не так уж важно, поскольку, если вы принимаете Версию ИИ Тезиса Ч-Т, ни одна из этих альтернатив невозможна. Утверждение, что ни в какой формальной системе не существует разрешающей процедуры, способной отличать теоремы от не-теорем называется Теоремой Черна. Утверждение, что ни в какой формальной системе не существует разрешающей процедуры для Истины ТТЧ — если таковая существует, в чем легко начать сомневаться после рассмотрения всех разветвлений ТТЧ, — следует из Теоремы Тарского (опубликованной в 1933 году, хотя Тарский был знаком с подобными идеями значительно раньше).
Доказательства этих двух важных результатов метаматематики весьма схожи. Оба вытекают из автореферентных построений. Давайте сначала рассмотрим вопрос о разрешающей процедуре для теоремности ТТЧ. Если бы существовал некий способ, при помощи которого можно было бы сказать, принадлежит ли данная формула X к классу «теорем» или «не-теорем», то, согласно Стандартной Версии Тезиса Ч-Т, должна была бы существовать некая конечная программа Флупа (общерекурсивная функция), которая могла бы проделать то же самое, когда входными данными является Гёделев номер формулы X. Важно помнить, что любое свойство, которое может быть проверено при помощи конечной программы Флупа, представимо в ТТЧ. Но, как мы вскоре увидим, это было бы источником проблем, поскольку если теоремность — представимое свойство, то Гёделева формула G становится так же порочна, как и парадокс Эпименида.
Все зависит от того, что утверждает G: «G — не теорема ТТЧ». Предположим, что G была бы теоремой. Тогда, поскольку теоремность, по предположению, представима, то формула ТТЧ, утверждающая «G — теорема ТТЧ», была бы теоремой ТТЧ. Но эта формула — не что иное как ~G, отрицание G; выходит, что ТТЧ непоследовательна. Предположим теперь, что G — теорема. Тогда опять, поскольку мы предполагаем, что теоремы представимы, формула, утверждающая «G — не теорема» являлась бы теоремой ТТЧ. Но эта формула — не что иное, как G; мы снова получаем парадокс. В отличие от ранее описанной ситуации, этот парадокс не имеет решения. Проблема заключается в начальном предположении, что свойство теоремности представлено некоей формулой ТТЧ; следовательно, нам придется отказаться от этого предположения. Это заставляет нас признать, что не существует программы Флупа, способной отличить Гёделевы номера теорем от Гёделевых номеров не-теорем. Наконец, если мы принимаем Версию ИИ Тезиса Ч-Т, мы должны пойти еще дальше и заключить, что не существует такого метода, при помощи которого люди могут отличать теоремы от не-теорем (и это включает методы, основанные на восприятии красоты). Сторонники Версии Коллективных Процессов все еще могут полагать, что Крабьи способности возможны; но из всех версий именно эту труднее всего подтвердить фактами.
Теорема Тарского
Теперь давайте рассмотрим результат Тарского. Тарский хотел выяснить, существует ли способ выразить в ТТЧ понятие теоретико-численной истины. То, что теоремность можно выразить (но не представить), мы уже видели; Тарский задался аналогичным вопросом в приложении к понятию истины. Точнее, он хотел определить, есть ли формула ТТЧ с единственной свободной переменной а, которая может быть интерпретирована как:
«Формула, чей Гёделев номер — а, выражает истину.»
Предположим, вместе с Тарским, что такая формула существует. Для краткости назовем ее ISTIN{a}. Теперь используем метод диагонализации и построем высказывание, утверждающее о себе самом, что оно ложно. Для этого мы точно повторим метод Гёделя, начиная с «дяди»:
Ea:<~ISTIN{a}ΛARITHMOQUINE{a'',a}>
Предположим, что Гёделев номер этого дяди — t. Арифмоквайнируем теперь самого дядю и получим формулу Тарского Т:
Ea:<~ISTIN{a}ΛARITHMOQUINE{SSS...SSS/a'',a}>
. |______| S повторяется t раз
В интерпретации эта формула читается как:
«Арифмоквайнификацией t является ложное утверждение.»
Но, поскольку арифмоквайнификация t — это собственный Гёделев номер Т, формула Тарского Т в точности воспроизводит парадокс Эпименида внутри ТТЧ, говоря о себе «Я — ложь». Разумеется, это ведет к заключению, что это высказывание одновременно является и истинным и ложным (либо ни тем, ни другим). Возникает интересный вопрос: что плохого в воспроизведении парадокса Эпименида? Какие от этого могут быть последствия? В конце концов, этот парадокс уже существует в русском языке, и русский язык пока от этого не погиб.
Магиификраб невозможен
Ответ заключается в том, что здесь имеются два уровня значения. Один из них мы только что использовали; другой уровень — это утверждение теории чисел. Если бы формула Т Тарского действительно существовала, то она являлась бы высказыванием о натуральных числах, которое одновременно и истинно и ложно! Именно в этом вся загвоздка. В то время как мы можем отмахнуться от парадокса Эпименида в русском языке, сказав, что его тема (его собственная истинность) — это нечто абстрактное, дело меняется, когда речь идет о конкретных высказываниях о числах! Если мы решим, что такая путаница не должна существовать, то нам придется отказаться от предположения о существовании формулы ISTIN{a}. Следовательно, в ТТЧ невозможно выразить понятие истинности. Заметьте, что это делает истину еще более неуловимым понятием, чем теоремность, поскольку та, по крайней мере, выразима. Те же самые аргументы приводят нас к заключению, что:
крабий ум не способен распознавать истину, точно так же как он не способен распознавать теоремность ТТЧ.
Первое противоречило бы Теореме Тарского-Чёрча-Тюринга («Не существует разрешающей процедуры для арифметических истин»), а второе — Теореме Чёрча.
Два вида формы
Интересно подумать о значении слова «форма» в приложении к построению сложных фигур. Например, что заставляет нас признать картину красивой? «Форма» линий и точек на нашей сетчатке? По-видимому, так и должно быть, поскольку именно в этой форме картина передается анализирующим механизмам у нас в голове; однако сложность обработки этих данных вызывает у нас чувство, что мы смотрим на что-то большее, чем простая двухмерная поверхность, — мы отвечаем на некое внутреннее значение картины, ее многомерный аспект, заключенный внутри этих двух измерений. Здесь важно слово «значение». Наш разум оснащен переводчиками, производящими на основе двухмерных схем многомерные значения, такие сложные, что мы не можем их описать сознательно. То же самое можно сказать и о нашей реакции на музыку.
Субъективно может показаться, что механизм, извлекающий внутреннее значение, совершенно отличен от механизма, проверяющего наличие или отсутствие некоего определенного качества, такого, например, как правильно-сформированность строчек. Возможно, это потому, что внутреннее значение — это что-то, что проявляется со временем.
Из этого следует, что в схемах, которые мы анализируем, можно говорить о двух видах формы. Прежде всего, там существуют такие качества, как правильно-сформированность, наличие которой можно определить с помощью предсказуемо конечных тестов, как в программах Блупа. Я предлагаю называть это синтаксическими характеристиками формы. Интуитивно можно сказать, что синтаксические аспекты формы лежат близко к поверхности и, таким образом, не создают многомерных познавательных структур.
С другой стороны, семантические характеристики формы не могут быть проверены с помощью предсказуемо конечных тестов; для них требуются открытые тесты. Примером такого аспекта, как мы видели, является теоремность строчек ТТЧ. Мы не можем, использовав некий стандартный тест, установить, является ли данная строчка теоремой ТТЧ. Почему-то тот факт, что здесь идет речь о значении, важным образом соотносится с трудностью определения теоремности ТТЧ. Акт извлечения значения из строчки означает, по сути, установление всех связей данной строчки с остальными строчками, и это, в свою очередь, выводит нас на бесконечную дорогу. Таким образом, «семантические» характеристики соотносятся с открытым поиском, поскольку — и это очень важно — значение объекта не заключается внутри самого объекта. Это не означает, что никакой объект вообще никогда невозможно понять, поскольку со временем его значение становится все яснее. Однако некоторые аспекты значения останутся скрыты очень надолго.
Значение вытекает из отношения к познавательным структурам
Давайте перейдем от строчек ТТЧ к музыкальным произведениям. Если вам так больше нравится, можете продолжать употреблять слово «строчка» в применении к музыкальным пьесам. Это обсуждение весьма общее, но мне кажется, что его смысл легче передать на примере музыки. Значение музыкального произведения странным образом дуалистично: с одной стороны оно тесно соотносится с огромным количеством других вещей в мире, а с другой стороны, оно явно выводится из самой музыки, то есть, оно должно быть расположено где-то внутри музыкального произведения.
Решение этой дилеммы включает понятие интерпретатора — механизма, извлекающего значение. (Под «интерпретатором» в этом контексте я подразумеваю не музыканта-исполнителя, а механизм в мозгу у слушателя, извлекающий значение из пьесы, которую тот слышит.) Интерпретатор может заметить многие важные аспекты значения пьесы, слушая ее в первый раз; это, по-видимому, подтверждает гипотезу о том, что значение находится в самой пьесе и просто извлекается из нее. Но это только полдела. Музыкальный интерпретатор действует, создавая многомерную мысленную структуру — внутреннее представление о пьесе, — которую он пытается соотнести с ранее известной информацией, находя связи с другими многомерными мысленными структурами, в которых закодирован предыдущий опыт. По мере того, как происходит этот процесс, полное значение пьесы постепенно выходит на поверхность. В действительности, могут пройти годы прежде чем мы почувствуем, что наконец-то поняли сокровенное значение определенной пьесы. Это, как кажется, поддерживает гипотезу о том, что значение музыкального произведения также находится и вне его и что роль интерпретатора — постепенно собрать это значение воедино.
Без сомнения, истина лежит где-то посередине значения — как музыкальное, так и лингвистическое — до какой-то степени локализованы только отчасти. Используя терминологию главы VI, мы можем сказать, что музыкальные произведения и куски текста отчасти являются триггерами, и отчасти — носителями явного значения. Яркая иллюстрация этого дуализма — табличка со старинной надписью значение здесь частично хранится в библиотеках и мозгах ученых всего мира, и в то же время явно содержится в самой табличке.
Таким образом, еще один способ охарактеризовать различие между «синтаксическими» и «семантическими» свойствами (в только что описанном смысле) заключается в том, что синтаксические свойства безусловно находятся внутри самого объекта, в то время как семантические свойства зависят от отношений этого объекта с потенциально бесконечным множеством других объектов и, следовательно, не являются полностью локализуемыми В синтаксических свойствах в принципе нет ничего спрятанного и загадочного, в то время как спрятанность — суть семантических свойств. Именно поэтому я предложил различать между «синтаксическим» и «семантическим» аспектами зрительных образов.
Красота, Истина и Форма
А как насчет красоты? Согласно вышеизложенным идеям, это, безусловно, не синтаксическое свойство Семантическое ли это свойство? Свойство ли это, скажем, отдельной картины? Давайте рассмотрим этот вопрос в применении к единственному зрителю С каждым из нас бывало, что то, что когда-то казалось красивым, некоторое время спустя выглядит серым и скучным, а в промежутках, возможно, кажется нейтральным Значит ли это, что красота — свойство преходящее? Можно повернуть ту же ситуацию другим концом и сказать, что изменился зритель. Но, имея в виду определенного зрителя, определенную картину и определенный момент времени, можно ли утверждать, что красота — качество, которое либо присутствует, либо нет? Или же красота неопределима и неуловима?
Возможно, что в каждом человеке в зависимости от обстоятельств могут действовать различные уровни интерпретаторов. Эти разные интерпретаторы выдают разные значения, устанавливают разные связи и обычно оценивают все глубокие аспекты по-разному. Из-за этого понятие красоты кажется почти неопределимым. Именно по этой причине я решил связать красоту в Диалоге «Магнификраб» с истиной, которая, как мы видели, является одним из самых неуловимых понятий математики.
Нейронный субстрат парадокса Эпименида
В заключение этой главы я хочу привести некоторые идеи, касающиеся основной проблемы истины, парадокса Эпименида. Мне кажется, что воспроизведение Тарским этого парадокса в ТТЧ позволяет глубже понять его природу в русском языке. Тарский нашел, что в его версии парадокса есть два разных уровня. На одном уровне это суждение о себе самом, которое было бы истинно, если бы оно было ложно и ложно, если бы оно было истинно. На другом уровне — который я буду называть арифметическим субстратом — это суждение о целых числах, истинное тогда и только тогда, когда оно ложно.
Почему-то это последнее раздражает нас гораздо больше первого. Некоторые люди просто отмахиваются от первого уровня, как от «бессмыслицы», из-за его автореферентности. Но отмахнуться от парадоксального суждения о целых числах невозможно. Суждения о целых числах просто не могут быть одновременно и истинными, и ложными.
Мне кажется, что превращение Тарским парадокса Эпименида учит нас искать субстрат также в языковой версии парадокса. В арифметической версии высший уровень значения опирается на низший арифметический уровень. Аналогично, автореферентное суждение, которое мы воспринимаем («Это высказывание ложно») может являться только высшим уровнем некой конструкции с двумя уровнями. Что же тогда играет здесь роль низшего уровня? Какой механизм порождает язык? Мозг. Значит, необходимо искать нейронный субстрат парадокса Эпименида — низший уровень противоречащих друг другу физических событий, то есть событий, которые не могут произойти одновременно. Если такой физический субстрат существует, то тогда понятно, почему нам не удается разрешить парадокс Эпименида, — наш мозг пытается сделать нечто невозможное.
Что же это за конфликтующие физические события? Предположительно, когда вы слышите парадокс Эпименида, ваш мозг «кодирует» это предложение как внутреннюю конструкцию взаимодействующих символов. После этого он пытается классифицировать предложение как «истинное» или «ложное». В процессе этого определения некоторые символы обязательно должны взаимодействовать. (Предположительно это происходит при обработке любого предложения.) Если при этом физически прерывается процесс кодификации предложения — нечто, чего обычно не происходит, — тогда начинаются неприятности, поскольку это все равно что пытаться заставить патефон проигрывать собственную разбивальную музыку. Мы описали происходящий конфликт в физических терминах, а не в терминах нейронов. Если наш анализ правилен, то мы сможем продолжить обсуждение, когда нам станет известно, как участвуют нейроны и схемы их возбуждения в построении символов в мозгу и каким образом там «кодируются» предложения.
Этот набросок нейронного субстрата парадокса Эпименида наводит (по-крайней мере, меня) на мысль о том, что решение языковой версии парадокса Эпименида может быть подобно решению версии Тарского — то есть, что нам придется отказаться от мысли, что мозг может когда-либо с точностью представить понятие истины. Новым здесь является предположение, что полное воспроизводство истины невозможно по физическим причинам, поскольку оно включало бы физически несовместимые мозговые процессы.
Назад: Магнификраб в пирожоре
Дальше: ШРДЛУ

