ГЛАВА IV: Непротиворечивость, полнота и геометрия
Смысл явный и неявный
В главе II мы видели пример того, как смысл — по крайней мере, в относительно простом контексте формальных систем — рождается из изоморфизма между управляемыми правилами символами и вещами реального мира. В большинстве случаев, чем сложнее изоморфизм, тем больше «техники» — как аппаратуры, так и программного обеспечения — бывает необходимо, чтобы извлечь смысл из символов. Если изоморфизм очень прост (или хорошо нам знаком), то есть соблазн считать, что смысл, который мы замечаем, выражен явно. Мы видим смысл, не замечая изоморфизма. Один из самых ярких тому примеров — человеческий язык. Люди часто приписывают значения самим словам, абсолютно не осознавая существования сложного «изоморфизма», эти значения порождающего. Эту ошибку совершить нетрудно; она состоит в том, что значение приписывается скорее объекту (слову), чем связи между данным объектом и реальностью. Вы можете сравнить это с наивным представлением о том, что шум является необходимым побочным эффектом столкновения двух предметов. Это, разумеется, неверно если два предмета столкнутся в вакууме, столкновение будет совершенно бесшумным. Здесь ошибка также заключается в том, что шум приписывается исключительно столкновению, и при этом игнорируется роль среды, переносящей звук от столкнувшихся предметов к уху.
Выше я использовал слово «изоморфизм» в кавычках, чтобы показать, что его здесь надо понимать с долей скептицизма. Символические процессы, лежащие в основе человеческого языка, настолько неизмеримо сложнее символических процессов в формальных системах, что, если мы хотим по-прежнему считать, что значение — порождение изоморфизмов, то нам придется принять более гибкое определение изоморфизма, чем то, каким мы пользовались до сих пор. Мне кажется, что именно понимание природы изоморфизма, стоящего за значением, — ключ к загадке человеческого сознания.
Явный смысл «Акростиконтрапунктуса»
Все это было подготовкой к обсуждению «Акростиконтрапунктуса» — исследованию уровней его значения. В Диалоге есть как явный, так и неявный смысл. Самое явное значение — та история, которая в нем рассказана. Это «явное» значение, строго говоря, крайне неявно — ведь мозгу приходится проделать невероятно сложную работу, чтобы, основываясь на черных значках на бумаге, понять происходящие в этой истории события. Несмотря на это, мы будем считать эти события явным значением Диалога, предполагая, что любой русскоязычный читатель, извлекая смысл из значков на бумаге, использует более или менее одинаковый «изоморфизм».
И все же, я хотел бы сделать явное значение истории еще более явным. Сначала немного о пластинках и патефонах. Обратите внимание на то, что дорожки на пластинке имеют два уровня значения. Первый уровень — музыка. Но что же такое музыка — последовательность колебаний в воздухе или последовательность эмоциональных реакций в человеческом мозгу? И то и другое, скажете вы. Но для того, чтобы эти эмоции возникли, сначала необходимы колебания. Колебания «извлекаются» из звуковых дорожек при помощи патефона — относительно несложного устройства. На самом деле, вы можете сделать то же самое, ведя по дорожкам булавкой. После этого ухо превращает колебания в реакции слуховых нейронов мозга, которые, в свою очередь, трансформируют линейную последовательность вибраций в схему взаимодействующих эмоциональных откликов. Схема эта настолько сложна, что мне придется, вопреки желанию, воздержаться от ее обсуждения здесь. Так что давайте пока считать, что звуки в воздухе — это «Первый Уровень» значения звуковых дорожек. Что же является «Вторым Уровнем» их значения? Это та вибрация, которая возникает в патефоне. Поэтому Второй Уровень значения зависит от цепи двух изоморфизмов:
(1) изоморфизм между произвольным узором звуковых дорожек и колебаниями воздуха;
(2) изоморфизм между произвольными колебаниями воздуха и вибрацией патефона.
Эта цепь двух изоморфизмов изображена на рис. 20. Обратите внимание, что изоморфизм 1 порождает Первый Уровень значения. Второй Уровень значения — менее явный, чем Первый, поскольку он порожден двумя изоморфизмами. Именно Второй Уровень значения является виновником того, что патефон разбивается. Интересно то, что рождение Первого Уровня значения немедленно влечет за собой рождение Второго Уровня значения — один уровень невозможен без другого. Таким образом, именно неявное значение пластинки «атаковало» и разрушило патефон. Те же комментарии приложимы и к бокалу. Разница лишь в том, что здесь имеется еще один уровень изоморфизма — соответствие между музыкальными нотами и буквами алфавита — который мы будем называть «транскрипцией». За ней следует «перевод»: превращение музыкальных нот в звуки, после чего вибрация действует на бокал точно так же, как она действовала на серию все усложняющихся патефонов.
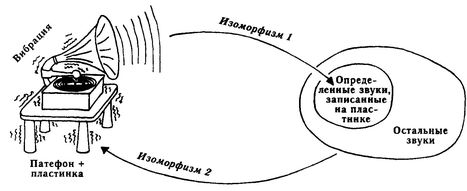
Рис. 20. Наглядное объяснение принципа, лежащего в основе Теоремы Геделя: два тесно связанных изоморфизма, дающие неожиданный эффект бумеранга. Первый — от звуковых дорожек к звуку, получаемый при помощи патефона. Другой — знакомый всем нам, но обычно оставляемый без внимания — от звука к вибрации патефона. Обратите внимание на то, что второй изоморфизм существует независимо от первого: не только музыка, играемая на патефоне, но и вообще все звуки вблизи от него вызывают в нем вибрацию. Перефразировка Теоремы Геделя звучит так: для любого патефона существуют такие пластинки, которые нельзя на нем проигрывать, так как это косвенно способствует разрушению патефона. (Рисунок автора.)
Неявные значения «Акростиконтрапунктуса»
Что же можно сказать о неявных значениях Диалога? (Множественное число не случайно — в Диалоге их несколько.) О самом простом из них мы уже упомянули выше — события в двух частях Диалога приблизительно изоморфны: патефон становится скрипкой, Черепаха — Ахиллом, Краб — Черепахой, звуковые дорожки — выгравированным автографом, и т. д. После того, как вы заметили этот простой изоморфизм, вы можете продвинуться дальше. Обратите внимание, что в первой половине истории Черепаха — виновник всех проказ, в то время как во второй половине она — жертва. Ее же собственный метод обратился против нее! Не напоминает ли это вам об «атаке» на патефон пластинок, которые на нем проигрывают, или о надписи на бокале, явившейся «виновницей» его гибели, или о Черепахиной коллекции бумерангов? Безусловно. Это — история о «плевках против ветра» на двух уровнях:
Первый уровень: «самоатакующие» бокалы и пластинки;
Второй уровень: «самоатакующий» дьявольский метод Черепахи, использующий для «самоатаки» неявные значения.
Таким образом, мы можем установить изоморфизм между двумя уровнями истории, сравнив то, как пластинки и бокалы, подобно бумерангам, «замыкаются» сами на себя и в результате гибнут, с тем, как предательский метод Черепахи оборачивается против нее самой. Рассматриваемая таким образом, сама история — пример «самоатак», которые в ней обсуждаются. Поэтому мы можем считать, что «Акростиконтрапунктус» косвенно говорит о себе самом, в том смысле, что его структура изоморфна событиям, которые в нем происходят. (Совершенно так же, как пластинки и бокал косвенно «говорят» о себе самих путем соседствующих изоморфизмов между игрой и вызыванием вибрации.) Конечно, можно прочитать Диалог, не замечая этого изоморфизма; тем не менее, он там присутствует.
Соответствие между «Акростиконтрапунктусом» и Теоремой Гёделя
Читатель, возможно, уже чувствует некоторое головокружение — однако это еще только цветочки, а ягодки впереди. (На самом деле, некоторые уровни неявного значения даже не будут здесь затронуты — если пожелаете, можете попробовать докопаться до них сами.) Я написал этот Диалог в основном для того, чтобы проиллюстрировать Теорему Гёделя, которая, как я уже говорил во введении, зависит от двух различных уровней значения высказываний теории чисел. Каждая из двух половин Диалога — «изоморфная копия» Теоремы Гёделя. Поскольку это сложное соответствие — центральная идея диалога, я попытался представить его на следующей диаграмме.
патефон <==> система аксиом теории чисел
патефон низкого качества <==> «слабая» система аксиом
качественный патефон <==> «сильная» система аксиом
«совершенный» патефон <==> полная система для теории чисел
«схема устройства» патефона <==> аксиомы и правила формальной системы
пластинка <==> строчка формальной системы
«проигрываемая» пластинка <==> теоремы формальной системы
«непроигрываемая» пластинка <==> не-теоремы формальной системы
звук <==> истинное высказывание теории чисел
воспроизводимый звук <==> интерпретированная теорема системы
невоспроизводимый звук <==> истинное высказывание, не являющееся теоремой
название песий «Меня нельзя воспроизвести на патефоне X» <==> неявное значение строчки Геделя «Меня нельзя вывести в формальной системе X»
На этой диаграмме приводится основа изоморфизма между Теоремой Гёделя и «Акростиконтрапунктусом». Не волнуйтесь, если вы пока не вполне понимаете суть Теоремы Гёделя — мы дойдем до нее только через несколько глав! Однако, прочитав этот Диалог, вы уже до некоторой степени прониклись духом этой Теоремы, даже если это и произошло незаметно для вас самих. Теперь я оставляю вас, читатель, с тем, чтобы вы попытались найти другие типы неявных значений в «Акростиконтрапунктусе». «Quaerendo invenietis»
«Искусство фуги»
Несколько слов об «Искусстве фуги»… Написанное в последний год жизни Баха, оно состоит из восемнадцати фуг, основанных на одной и той же теме. По-видимому, создание «Музыкального приношения» вдохновило Баха еще на один цикл фуг, на этот раз с менее сложной исходной темой, где он решил показать все возможности этой формы. Простую тему «Искусства фуги» Бах обыгрывает множеством разных способов. Большинство фуг четырехголосные; их сложность и глубина выражения постепенно возрастают. Ближе к концу фуги достигают такой степени сложности, что кажется невероятным, что композитору удается поддерживать этот уровень. Однако это ему удается… до последнего «Контрапункта».
«Искусство фуги» (а также жизнь композитора) были прерваны следующими обстоятельствами: Бах, у которого в течение многих лет были проблемы со зрением, наконец решился на операцию. Операция прошла неудачно, и Бах ослеп. Однако это не остановило его от работы над монументальным проектом, целью которого было описание всех возможностей искусства полифонической композиции; одной из важных черт проекта было использование многих тем. В композицию, которая была задумана как предпоследняя, Бах включил собственное имя, закодированное в третьей теме. Однако сразу после этого его здоровье так ухудшилось, что работу над любимым проектом пришлось прекратить. Несмотря на болезнь, Баху удалось продиктовать своему зятю финальную хоральную прелюдию, о которой Форкель, биограф композитора, написал следующее: «Когда я исполняю эту прелюдию, я всегда бываю глубоко тронут духом набожного смирения и веры; не могу сказать, чего мне не хватало бы больше: этого Хорала, или окончания последней фуги.»
Незадолго до смерти к Баху неожиданно вернулось зрение. Через несколько часов после этого с ним случился удар, и десять дней спустя он скончался, оставив загадку неполноты своего «Искусства фуги». Не связано ли это с тем, что Бах использовал там автореференцию?
Проблемы, связанные с Гёделевским результатом
Черепаха утверждает, что никакой достаточно мощный патефон не может быть совершенен — то есть способен воспроизвести любые звуки, записанные на пластинке. Гёдель утверждает, что никакая достаточно мощная формальная система не может быть совершенна — то есть способна представить любое истинное высказывание в виде теоремы. Так же, как и в случае с патефонами, это кажется дефектом только тогда, когда мы предъявляем слишком высокие требования к возможностям формальных систем. Однако для математиков начала столетия подобные завышенные требования были обычным делом; в то время во всемогуществе логических рассуждений никто не сомневался. Доказательство обратного было найдено в 1931 году. Тот факт, что в любой достаточно сложной формальной системе истинных утверждений больше, чем теорем, называется «неполнотой» этой системы. Удивительно то, что методы рассуждения, используемые Гёделем в его доказательстве, по-видимому, невозможно заключить в рамки формальных систем. С первого взгляда кажется, что Гёделю впервые удалось выразить необычайно глубокую и важную разницу между человеческой логикой и логикой машины. Это загадочное несоответствие между мощью живых и неживых систем отражено в несоответствии между понятием «истинности» и понятием «теоремности»; таков возможный романтический взгляд на эту ситуацию.
Модифицированная система pr и противоречивость
Чтобы взглянуть на ситуацию более реалистично, нам необходимо глубже понять, почему и каким образом смысл выражается в формальных системах при помощи изоморфизма. (Мне кажется, что на самом деле это приводит к еще более романтическому взгляду на вещи.) Итак, сейчас мы приступаем к изучению некоторых новых для нас аспектов отношения между значением и формой. Первым делом, давайте создадим новую формальную систему, чуть-чуть изменив нашу старую знакомую, систему пр. Добавим к ней еще одну схему аксиом, сохранив при этом как старую схему, так и единственное правило вывода.
СХЕМА АКСИОМ II: Если x является строчкой тире, то xp-rx будет аксиомой.
Ясно, что как --p-r--, так и --p-r--- будут теоремами новой системы. Однако они интерпретируются, соответственно, как «2 плюс 1 равняется 2» и «2 плюс 2 равняется 3». Легко увидеть, что такая система будет содержать массу ложных высказываний (если считать строчку высказыванием). Таким образом, наша новая система противоречива по отношению к окружающему миру.
Как говорится, беда не приходит одна, в новой системе есть также и внутренние проблемы. Она содержит высказывания, противоречащие друг другу, такие как -p-r-- (старая аксиома) и -p-r- (новая аксиома). Это означает, что наша система противоречива также и в другом смысле — внутренне.
Так что же, лучше совсем отказаться от новой системы?
Ни в коем случае! Я нарочно описал эти «противоречия» в «лапшевешательном» стиле, изложив довольно туманные аргументы с уверенностью, призванной запутать читателя. Вполне возможно, что вы уже заметили ошибки в моих рассуждениях. Основная ошибка состоит в том, что я безоговорочно принял для новой системы ту же интерпретацию, что была верна для прежней системы. Вспомните, что мы тогда остановились на словах «плюс» и «равняется» только потому, что в такой интерпретации символы действовали изоморфно понятиям, с которыми мы их сравнивали. Когда мы изменяем правила системы, этот изоморфизм неизбежно страдает. С этим ничего не поделаешь. Таким образом, проблемы, на которые я жаловался в предыдущих абзацах, могут рассеяться как дым, как только мы найдем подходящую интерпретацию для некоторых символов новой системы. Обратите внимание, что я сказал «некоторых» — совсем не обязательно в каждом случае менять интерпретацию всех символов. Некоторые из них могут сохранить прежнее значение, в то время как другие изменятся.
Снова непротиворечивость
Предположим, например, что мы интерпретируем по-новому лишь символ r, оставляя все остальные символы без изменения; в частности, символ r будет означать «больше или равно». Теперь наши «противоречивые» теоремы -p-r- и -p-r-- звучат совершенно безобидно: «1 плюс 1 больше или равно 1» и «1 плюс 1 больше или равно 2». Мы одновременно избавились от противоречий (1) с окружающим миром и (2) внутри системы. К тому же, наша новая интерпретация значима, в то время как прежняя не имела смысла. Я имею в виду, что она не имела смысла в новой системе — в нашей первоначальной системе pr она работала превосходно. Пытаться же использовать ее в новой системе так же глупо, как использовать интерпретацию «лошадь-яблоко-счастливая» в старой системе pr.
История эвклидовой геометрии
Несмотря на мои попытки застать вас врасплох и сбить с толку, этот урок по интерпретации символов при помощи слов, возможно, не показался вам слишком трудным, как только вы поняли, в чем тут дело. Действительно, это несложно. Однако это было одним из глубочайших прозрений математики девятнадцатого века! Все началось с Эвклида, который около 300 года до нашей эры собрал и систематизировал все, что было известно о геометрии в то время. Получившийся труд оказался таким солидным, что в течение более чем двух тысячелетий он практически считался библией геометрии — одна из наиболее «долголетних» работ! Почему так получилось?
Основная причина в том, что Эвклид был основоположником строгости в математических рассуждениях. Его «Элементы» начинаются с простых понятий, определений и так далее; при этом постепенно накапливается множество результатов, организованных таким образом, что каждый данный результат строго основан на предыдущих. В результате, работа имела определенный план, архитектуру, делавшую ее мощной и прочной.
Однако эта архитектура весьма отличалась от, скажем, архитектуры небоскреба. (См. рис. 21.) В последнем случае, сам факт того, что небоскреб стоит и не падает, доказывает, что его структура «правильна». С другой стороны, в книге по геометрии, где предполагается, что каждое утверждение логически следует из предыдущих, одно ошибочное доказательство не вызовет видимого краха всей структуры. Перекладины и подпорки здесь не физические, а абстрактные. На самом деле, в Эвклидовых «Элементах» доказательства были построены из весьма капризного материала, полного скрытых ловушек. Этим материалом был человеческий язык. Как же в таком случае быть с архитектурной мощью «Элементов»? Верно ли, что они основаны на прочной структуре, или же в ней есть некие изъяны?

Рис. 21. М. К. Эшер «Вавилонская башня» (гравюра на дереве, 1928)
Каждое слово, которое мы произносим, имеет определенный смысл, диктующий нам, как это слово использовать. Чем обычнее слово, тем больше ассоциаций связано с ним и тем глубже укоренилось в нас его значение. Таким образом, когда кто-то пытается дать определение какому-либо употребительному слову, в надежде на то, что все мы с этим определением согласимся, обычно происходит следующее: вместо того, чтобы принять данное нам определение, мы, по большей части бессознательно, предпочитаем руководствоваться ассоциациями, хранящимися на «складе» нашего мозга. Я упоминаю об этом потому, что именно с такой проблемой столкнулся Эвклид, пытаясь дать определения таких обыденных слов как «точка», «прямая линия», «круг» и так далее. Как можно определить нечто, о чем у каждого уже есть вполне сформировавшаяся идея? Единственный способ заключается в том, чтобы указать, что ваше слово — технический термин, который не должно путать с обычным, повседневным словом. Необходимо подчеркнуть, что связь с обычным значением слова здесь лишь кажущаяся. Эвклид этого не сделал, так как он был убежден в том, что точки и прямые в его «Элементах» были, на самом деле, точками и прямыми реального мира. Эвклид не предостерег читателей от ложных ассоциаций, тем самым пригласив их к свободной игре воображения…
Это звучит почти анархично и, пожалуй, немного несправедливо по отношению к Эвклиду — ведь он установил аксиомы или постулаты, которые должны были использоваться при доказательстве утверждений. На самом деле, он считал, что доказательства должны были быть основаны исключительно на этих аксиомах и постулатах. К несчастью, именно здесь и случилась осечка! Неизбежным следствием использования ординарных слов явилось то, что некоторые вызванные этими словами ассоциации проникли и в Эвклидовы доказательства. Однако не думайте, что, читая «Элементы», вы найдете там зияющие «провалы» в рассуждениях. Напротив, ошибки там почти незаметны, поскольку Эвклид был слишком глубоким и проницательным мыслителем, чтобы допускать элементарные промахи. Тем не менее, в его рассуждениях все-таки есть «прорехи» — небольшие дефекты в классическом труде. Однако вместо того, чтобы жаловаться, мы можем выучить кое-что новое о разнице между абсолютной и относительной строгостью математических рассуждений. На самом деле, именно отсутствие абсолютной строгости в работе Эвклида явилось причиной многих плодотворных открытий в математике более чем через две тысячи лет после того, как он написал свой труд.
Эвклид привел пять постулатов, легших в фундамент бесконечного небоскреба геометрии (Эвклидовы «Элементы» составили лишь первые несколько сотен этажей этого небоскреба). Четыре первые постулата кратки и элегантны:
(1) Любые две точки могут быть соединены отрезком прямой;
(2) Любой отрезок прямой может быть продолжен бесконечно и превращен в прямую линию;
(3) На основе любого отрезка прямой можно нарисовать круг, принимая этот отрезок за радиус и один из его концов — за центр круга;
(4) Все прямые углы конгруэнтны.
Пятый постулат далеко не так грациозен:
(5) Если две прямые пересекают третью так, что сумма внутренних углов с одной стороны меньше двух прямых углов, то это прямые рано или неизбежно пересекутся на этой стороне.
Хотя Эвклид нигде не сказал об этом прямо, он считал свой пятый постулат в каком-то смысле хуже других, поскольку он нигде не использовал его в доказательстве первых двадцати восьми утверждений. Таким образом, мы можем сказать, что эти утверждения составляют так называемую «геометрию четырех постулатов» — ту часть геометрии, которая может быть выведена на основе первых четырех постулатов «Элементов», без помощи пятого. (Ее также часто называют абсолютной геометрией.) Безусловно, Эвклид предпочел бы найти доказательство этого «гадкого утенка», но за неимением такового, утенка пришлось принять на веру…
Ученики Эвклида также были не в восторге от пятого постулата. В течение многих лет несказанное количество математиков посвящало несказанное число лет своей жизни попыткам доказать, что сам пятый постулат — всего лишь часть геометрии четырех постулатов. К 1763 году были опубликованы по крайней мере двадцать восемь доказательств — и все ошибочные! (Они были раскритикованы в диссертации некоего Г. С. Клюгеля.) Во всех этих ошибочных доказательствах присутствовала путаница между повседневной интуицией и строго формальными свойствами. Пожалуй, можно сказать, что на сегодняшний день эти «доказательства» не представляют интереса ни для математиков, ни для историков; однако имеются и некоторые исключения.
Многоликий Неэвклид
Во времена Баха жил некий Джироламо Саккери 1667-1733), питавший надежду освободить труд Эвклида от всех его недостатков. Основываясь на своих работах в области логики, он решил подойти к доказательству пятого постулата по-новому: предположим, что мы принимаем за истинное утверждение, обратное данному постулату. Теперь попробуем работать с этим утверждением в качестве пятого постулата. Через некоторое время мы наверняка придем к противоречию. Поскольку никакая математическая система не может содержать противоречия, тем самым мы докажем несостоятельность нашего пятого постулата — а следовательно, состоятельность пятого постулата Эвклида. Необязательно вдаваться в подробности истории; достаточно сказать, что Саккери с большой изобретательностью начал работать над «Саккерианской геометрией», выводя одно утверждение за другим, пока ему не надоело. В один прекрасный день он решил, что очередное выведенное им утверждение «противно самому понятию прямой линии». Это, как ему показалось, было именно тем, чего он так долго искал — желанным противоречием! Сразу после этого, незадолго до смерти, Саккери опубликовал свой труд под названием «Эвклид, освобожденный от недостатков».
Этим он лишил себя большей доли посмертной славы, так как не подозревал, что открыл то, что стало позже известно под именем «гиперболической геометрии». Через пятьдесят лет после Саккери, Ж. Г. Ламберт повторил ту же попытку, на этот раз подойдя еще ближе к цели. Наконец, через сорок лет после Ламберта и через пятьдесят лет после Саккери, неэвклидова геометрия была признана как новая, полноправная область геометрии. На доселе прямой дороге математики появилась развилка. В 1928 году неэвклидова геометрия одновременно, по одному из необъяснимых совпадений, была открыта венгерским математиком Яношем (Иоганном) Больяйем, которому тогда был двадцать один год, и тридцатилетним русским, Николаем Лобачевским. По иронии судьбы, в том же году великий французский математик Адриен-Мари Лежандр решил, что он нашел доказательство пятого постулата Эвклида. Его рассуждения весьма напоминали рассуждения Саккери.
Кстати, отец Яноша, Фаркаш (или Волфганг) Больяй, близкий друг великого Гаусса, также вложил много сил в попытку доказать Пятый постулат. В письме к своему сыну он пытался отговорить того от подобных занятий:
Не пытайся пробовать этот подход к параллельным линиям. Я прошел этот путь до самого конца. Я пережил эту бездонную ночь, погасившую всякий свет и радость в моей жизни. Молю тебя, оставь науку о параллельных прямых в покое. Я думал, что жертвовал собой во имя истины. Я был готов стать мучеником, который освободил бы геометрию от ее недостатков и, очищенную, возвратил бы ее человечеству. Я предпринял огромный, чудовищный труд; мои создания — неизмеримо лучше, чем у моих предшественников. И все же я не смог добиться полного удовлетворения. Поистине, si paullum a summo discessit, vergit ad imum . Убедившись, что ни один смертный не может достичь дна этой темной бездны, я повернул обратно, безутешный, жалея себя и все человечество… Я проплыл мимо всех рифов этого дьявольского мертвого моря, всегда возвращаясь со сломанной мачтой и разодранными в клочья парусами. Именно в это время у меня испортился характер и в жизни моей началась осень. Я легкомысленно поставил на карту мое счастье и саму мою жизнь — aut Caesar aut nihil.
Однако позже, убежденный, что его сын действительно чего-то достиг, Фаркаш настоятельно советовал ему опубликовать свои результаты, правильно предвидя такую частую в науке проблему одновременности:
Когда для определенных вещей пришло время, они появляются в разных местах, подобно тому, как фиалки появляются на свет ранней весной.
Насколько верным это оказалось в случае с неэвклидовой геометрией! В Германии сам Гаусс и еще несколько человек одновременно набрели на неэвклидовы идеи. Среди них были адвокат Ф. К. Швайкарт, который в 1818 году послал Гауссу письмо с описанием новой «астральной» геометрии, племянник Швайкарта Ф. А. Тауринус, который занимался неэвклидовой тригонометрией и Ф. Л. Вахтер, студент Гаусса, который умер в 1817 году в возрасте двадцати пяти лет, успев получить несколько глубоких результатов в неэвклидовой геометрии.
Ключом к неэвклидовой геометрии являлось «принятие всерьез» постулатов, на которых основаны такие геометрии как геометрия Саккери или Ламберта. Постулаты Саккери кажутся «отвратительными самой природе понятия прямой линии» только в том случае, если вы не можете освободиться от предвзятого мнения о том, что называть «прямой линией». Однако если вы можете отказаться от подобных идей и считать, что «простая линия» — это то, что удовлетворяет новым постулатам, то ваша точка зрения радикально изменится.
Неопределяемые понятия
Эти рассуждения, вероятно, уже начинают звучать знакомо. В частности, они возвращают нас к теме системы pr и ее варианта, где символы приобретали пассивное значение, зависящее от их роли в теоремах. Особенно интересен был символ r, поскольку его «значение» изменилось, когда мы прибавили новую схему аксиом. Совершенно так же значения понятий «точка», «линия» и т. д. могут определяться множеством теорем (или постулатов), в которых они встречаются. Очень важно, что открыватели неэвклидовой геометрии это осознали. Они нашли различные неэвклидовы геометрии, по-разному отрицая пятый постулат Эвклида и изучая последствия этого. Строго говоря, они (как и Саккери) не отрицали пятого постулата прямо; вместо этого они отрицали эквивалентный, так называемый параллельный постулат:
Через точку, лежащую вне прямой, можно провести одну и только одну прямую, не пересекающуюся с первой прямой, сколько бы мы их не продолжали.
В таком случае мы говорим, что вторая линия параллельна первой. Предполагая, что таких линий вообще не существует, вы входите в область эллиптической геометрии; утверждая же, что таких прямых существует по крайней мере две, вы оказываетесь в гиперболической геометрии. Говоря об этих вариантах, мы все еще используем термин «геометрия» поскольку в них присутствует основной элемент — абсолютная геометрия или геометрия четырех постулатов. Именно это «ядро» позволяет нам считать, что эти варианты — описания свойств некого геометрического пространства, хотя это пространство не так легко интуитивно представить, как обычное.
На самом деле, эллиптическую геометрию нетрудно представить зрительно. Все «точки», «линии» и т. д. должны быть частью поверхности обыкновенной сферы. Давайте условимся писать «ТОЧКА» когда имеется в виду технический термин, и «точка» — когда речь идет о повседневном значении. Мы можем сказать что ТОЧКА состоит из пары диаметрально противоположных точек на поверхности сферы. ЛИНИЯ — это большой круг на сфере (круг, центр которого, как и центр экватора, совпадает с центром самой сферы). В этой интерпретации утверждения эллиптической геометрии, хотя и содержат такие слова как «ТОЧКА» и «ЛИНИЯ», описывают происходящее на сфере, а не на плоскости. Обратите внимание, что две ЛИНИИ всегда пересекаются в диаметрально противоположных точках — а значит, в одной ТОЧКЕ! И, точно так же как две ЛИНИИ определяют ТОЧКУ, две ТОЧКИ определяют ЛИНИЮ.
Считая, что значения таких слов как «ТОЧКА» и «ЛИНИЯ» полностью зависят от утверждений, в которых эти слова встречаются, мы делаем шаг к полной формализации геометрии. Эта полуформальная версия еще употребляет множество слов русского языка в их обыденном значении («и», «если», «имеет», «соединяет» и т. п.), однако такие слова как «ТОЧКА» и «ЛИНИЯ» своего обыденного значения здесь лишены — поэтому мы называем их неопределяемые понятия. Неопределяемые понятия, такие как p и r системы pr, в каком-то смысле определены косвенно, — совокупностью всех утверждений, в которых они встречаются, — скорее чем прямо, в некоем определении.
Можно было бы утверждать, что полное определение неопределяемых понятий находится только в постулатах, так как там уже содержатся все вытекающие из них утверждения. Подобная точка зрения означала бы, что постулаты являются косвенными определениями всех неопределяемых понятий, поскольку те получают определение через какие-либо другие понятия.
Возможность множественных интерпретаций
Полная формализация геометрии означала бы, что каждый термин превратился бы в неопределяемое понятие, то есть стал бы «бессмысленным» символом какой-либо формальной системы. Я заключил слово «бессмысленный» в кавычки, поскольку, как вы знаете, символы автоматически приобретают различные пассивные значения, зависящие от теорем, в которых эти символы встречаются. Однако обнаружат ли люди эти значения — это уже другой вопрос, так как для этого необходимо найти такое множество понятий, которое может быть связано изоморфизмом с символами данной формальной системы. По идее, желая формализовать геометрию, мы обычно уже имеем в виду определенную интерпретацию для каждого символа, так что пассивные значения оказываются уже встроенными в систему. Именно это я и сделал с символами p и r, когда придумывал систему pr.
Но ведь могут существовать и другие пассивные значения, которые, в принципе, возможно подметить — только до сих пор еще никто этого не сделал! Например, первоначальная система pr допускала довольно неожиданную интерпретацию r как «равняется» и p как «отнятое от». Хотя это довольно тривиальный пример, он неплохо передает суть идеи о том, что символы могут иметь множество значимых интерпретаций; искать их — дело наблюдателя!…
Все, что мы до сих сказали, может быть сведено к понятию «непротиворечивости». Мы начали с введения формальной системы, которая, на первый взгляд, не только находилась в противоречии с внешним миром, но и имела внутренние противоречия. Однако через несколько минут нам пришлось взять эти «обвинения» обратно и признать свою ошибку; оказывается, дело было в том, что мы выбрали неудачную интерпретацию для символов системы. Изменив интерпретацию, мы вернули системе ее непротиворечивость! Становится ясно, что непротиворечивость — не свойство формальных систем как таковых, но зависит от интерпретации, предложенной для данной системы. Совершенно так же не является свойством формальных систем как таковых и противоречивость.
Разные виды непротиворечивости
Все это время мы говорили о «непротиворечивости» и «противоречивости», не давая определений этим понятиям. При этом мы опирались на старый добрый здравый смысл. Давайте теперь точно определим, что имеется в виду под непротиворечивостью формальной системы (вместе с ее интерпретацией). Это означает, что каждая теорема, будучи интерпретирована, становится истинным утверждением. С другой стороны, если среди интерпретированных теорем найдется хоть одно ложное утверждение, мы говорим о противоречивости данной системы.
Это определение говорит нам о противоречивости по отношению к внешнему миру — а как насчет внутренних противоречий? По идее, система была бы внутренне противоречива, если бы она содержала по крайней мере две теоремы, чьи интерпретации были бы несовместимы друг с другом, и непротиворечива, если бы все теоремы были совместимы между собой. Рассмотрим, например, формальную систему, имеющую только следующие три теоремы: ЧвЗ, ЗвЭ и ЭвЧ. Если Ч интерпретируется как «Черепаха», З — как «Зенон», Э — как «Эгберт» и x в y — как x всегда выигрывает в шахматы у «y», то мы имеем следующие интерпретированные теоремы:
Черепаха всегда выигрывает в шахматы у Зенона.
Зенон всегда выигрывает в шахматы у Эгберта.
Эгберт всегда выигрывает в шахматы у Черепахи.
Эти утверждения нельзя назвать несовместимыми, хотя они и описывают довольно странную компанию шахматистов. Таким образом, в этой интерпретации формальная система, в которой эти три строчки являются теоремами, внутренне непротиворечива, хота на самом деле ни одна из ее теорем не является истинной! Внутренняя непротиворечивость требует от теорем не того, чтобы все они были истинными, а лишь того, чтобы все они были совместимы друг с другом.
А теперь давайте предположим, что x в y интерпретируется как «x был изобретен y». Тогда у нас было бы:
Черепаха была изобретена Зеноном
Зенон был изобретен Эгбертом
Эгберт был изобретен Черепахой
В этом случае неважно, какие из отдельных высказываний истинны — а может быть, вообще нельзя установить, какие из них истинны и какие ложны. Однако мы можем с уверенностью сказать, что все три высказывания не могут быть истинными одновременно. Таким образом, данная интерпретация делает систему внутренне противоречивой. Противоречие здесь зависит не от интерпретации заглавных букв, а от интерпретации в и от того, как заглавные буквы передвигаются по кругу вокруг в. Следовательно, можно говорить о внутренней противоречивости, не интерпретируя всех символов системы. (В данном случае хватило интерпретации одного-единственного символа) Возможно, что интерпретировав достаточное количество символов, мы уже ясно увидим, что никакая дальнейшая интерпретация не сделает все теоремы истинными. Дело здесь, однако, не только в истине, а в возможности. Все три теоремы оказались бы ложными, если бы мы интерпретировали заглавные буквы как имена реальных персонажей, однако мы называем систему внутренне противоречивой по другой причине. Мы основываем наше суждение на интерпретации буквы в в сочетании с кругообразностью (Еще кое-что об этом «авторском треугольнике» вы найдете в главе XX).
Гипотетические миры и непротиворечивость
Мы привели два взгляда на непротиворечивость: первый утверждает, что система вместе с ее интерпретацией непротиворечива по отношению к внешнему миру, когда любая из ее интерпретированных теорем оказывается истинной. Другой говорит нам, что система вместе с ее интерпретацией внутренне непротиворечива, когда все ее теоремы, будучи интерпретированы, совместимы друг с другом. Эти два типа непротиворечивости тесно связаны. Чтобы определить совместимы ли друг с другом несколько высказываний, мы пытаемся представить себе такой мир, в котором все они могут быть истинными одновременно. Таким образом, внутренняя непротиворечивость зависит от непротиворечивости с внешним миром — только теперь «внешний мир» может быть любым воображаемым миром, вместо того, в котором мы живем. Однако это весьма неопределенное и неудовлетворительное заключение. Что составляет такой «воображаемый мир»? В конце концов, возможно вообразить и такой мир, в котором три героя изобретают друг друга по очереди. Или нет? Возможно ли вообразить мир, в котором есть квадратные круги? Или мир, в котором действительны законы Ньютона, а не законы относительности? Возможно ли вообразить такой мир, в котором что-то было бы одновременно зеленым и не зеленым? Или мир, в котором животные не сделаны из клеток? Мир, в котором Бах сымпровизировал восьмиголосную фугу на тему короля Фридриха Великого? В котором комары умнее людей? В котором Черепахи умеют играть в футбол и говорить? Разумеется, Черепаха, говорящая о футболе, была бы аномалией.
Некоторые из этих миров кажется легче вообразить, чем другие, так как некоторые из них включают логические противоречия — например, зеленый и не зеленый — в то время как другие кажутся, за неимением лучшего слова, возможными, сюда например, относятся Бах, импровизирующий восьмиголосную фугу, или животные, состоящие не из клеток. Или даже такие миры, в которых законы физики отличаются от наших… Пожалуй, можно сказать, что имеются разные типы непротиворечивости. Например, самым широким был бы «логически непротиворечивый» класс, так как для вхождения в него не существует никаких ограничений, кроме логических. Система является логически непротиворечивой, когда никакие из ее двух теорем, будучи интерпретированы как суждения, прямо не противоречат одна другой; математически непротиворечивой, когда интерпретированные теоремы не нарушают законов математики и физически непротиворечивой, когда интерпретированные теоремы совместимы с законами физики. За этим следует биологическая непротиворечивость и так далее. В биологически непротиворечивой системе может существовать теорема, интерпретация которой — суждение «Шекспир написал оперу», но не теорема, интерпретируемая как «Существуют неклеточные животные». Подобные причудливые типы противоречивости никто не изучает, так как их весьма сложно различить. Какая именно противоречивость заключена в задаче о трех героях, изобретающих друг друга по кругу? Логическая? Физическая? Биологическая? Литературная?
Обычно граница между интересным и неинтересным проводится между физической и математической непротиворечивостью. (Разумеется, эту линию проводят сами математики и физики — компания, которую вряд ли можно назвать беспристрастной!…) Это значит, что при рассмотрении формальных систем «учитываются» два типа противоречивости — математическая и логическая. В соответствии с этим критерием мы еще не нашли такой интерпретации, в которой тройка теорем ЧвЗ, ЗвЭ, ЭвЧ была бы противоречива. Для этого мы могли бы интерпретировать в как «больше чем». Как насчет Ч, 3, и Э? Они могут быть интерпретированы, например, как 0, 2 и 11, соответственно. Обратите внимание, что таким образом две теоремы оказываются истинными, и одна — ложной. Если бы мы интерпретировали З как 3, у нас получилось бы две ложных и одна истинная теорема. Однако в обоих случаях система была бы противоречива. На самом деле неважно, какое значение мы придаем Ч, З и Э, если мы не выходим за пределы натуральных чисел. Здесь мы опять сталкиваемся со случаем, когда, для того чтобы обнаружить внутреннюю противоречивость, необходима лишь частичная интерпретация символов системы.
Включение одной формальной системы в другую
Предыдущий пример, в котором были интерпретированы только некоторые из символов, чем-то напоминает занятия геометрией на натуральном языке, когда мы используем некоторые слова как неопределяемые понятия. В таком случае слова делятся на два класса: те, чье значение неизменно и четко определено, и те, чье значение меняется до тех пор, пока система не станет непротиворечивой.(Последние и являются неопределяемыми понятиями). Такой подход к геометрии требует, чтобы слова первого класса уже имели определения, приобретенные вне геометрии. Эти слова формируют скелет системы, ее глубинную структуру, которая может быть затем наполнена различным материалом (эвклидова или неэвклидова геометрия).
Формальные системы часто строятся именно по такому последовательному или иерархическому типу. Например, можно придумать Формальную Систему I, с правилами и аксиомами, дающими некие пассивные значения ее символам. Эта Формальная Система I включается в более широкую систему с большим количеством символов — Формальную систему II. Поскольку правила и аксиомы Формальной Системы I являются частью Формальной Системы II, пассивные значения символов Формальной Системы I остаются в силе и формируют жесткий скелет, играющий важную роль в определении пассивных значений новых символов Формальной Системы II. Вторая система может, в свою очередь, являться скелетом для третьей системы, и так далее. Может также существовать система (например, абсолютная геометрия) которая частично дает пассивные значения своих неопределяемых понятий и которая может быть дополнена правилами и аксиомами, далее ограничивающими эти значения. Именно это и происходит в случае эвклидовой геометрии в сравнении с неэвклидовой.
Уровни стабильности в зрительном восприятии
Подобным иерархическим образом мы приобретаем новые знания, расширяем наш словарный запас или воспринимаем незнакомые предметы. Это особенно интересно, когда мы пытаемся понять картины Эшера, скажем, такие, как «Относительность» (рис. 22), где часто встречаются совершенно невозможные образы. Можно предположить, что в таком случае мы должны пытаться интерпретировать картину снова и снова, пока не найдем непротиворечивой интерпретации — однако мы поступаем совершенно иначе. Мы сидим перед картиной, заинтригованные лестницами, ведущими во всех воображаемых направлениях, и людьми, идущими по одной и той же лестнице в противоречащих друг другу направлениях. Лестницы являются тем «островком уверенности», на котором мы основываем нашу интерпретацию всей картины. Увидев в них знакомый предмет, мы пытаемся затем установить, как они связаны друг с другом. На этом этапе мы сталкиваемся с проблемой. Однако если бы мы попытались отказаться от своих взглядов и поставить под сомнение сами «островки уверенности», то столкнулись бы с трудностями иного рода. Мы никак не можем «перерешить» то, что лестницы — это лестницы. Не рыбы, кнуты или руки, а именно лестницы. (На самом деле, выход у нас все-таки есть: можно оставить все линии картины вообще без интерпретации, как «бессмысленные символы» формальной системы. Этот путь — пример «способа U», или отношения дзен-буддизма к символизму.)

Рис. 22. М. К. Эшер. «Относительность» (литография, 1953).
Таким образом, иерархическая природа нашего восприятия заставляет нас видеть либо сумасшедший мир, либо кучу бессмысленных линий. Так же можно проанализировать и многие другие картины Эшера, опирающиеся на какие-либо стандартные формы, соединенные нестандартным образом. Когда зритель видит парадокс на высшем уровне, уже поздно возвращаться и пытаться поменять исходные интерпретации объектов нижнего уровня. Разница между рисунками Эшера и неэвклидовой геометрией заключается в том, что в последней возможно найти значимые интерпретации для неопределяемых понятий таким образом, что система становится понятной, в то время как в первой конечный результат несовместим с нашей концепцией мира, как бы долго мы не рассматривали картину. Конечно, можно придумать такие гипотетические миры, в которых Эшеровские события могут произойти… но эти миры подчинялись бы законам биологии, физики, математики и даже логики на одном уровне, одновременно нарушая их на другом уровне. Что за странные миры! (Примером этого может служить «Водопад» (рис. 5), где вода подчиняется нормальным законам гравитации, в то время как природа пространства идет вразрез с законами физики.)
Одинакова ли математика во всех возможных мирах?
До сих пор мы подчеркивали тот факт, что внутренняя непротиворечивость формальной системы (взятой вместе с ее интерпретацией) требует наличия некоего возможного мира, в котором все интерпретированные теоремы были бы истинны; единственным ограничением этого мира было бы то, что математика и логика работали бы в нем так же, как и в нашем мире. С другой стороны, внешняя непротиворечивость — непротиворечивость с внешним миром — требует того, чтобы все теоремы были бы истинны в реальном мире. В том случае, когда мы хотим создать непротиворечивую формальную систему, теоремы которой интерпретировались бы как математические суждения, разница между этими двумя типами непротиворечивости, по всей видимости, должна исчезнуть, поскольку мы только что сказали, что математика во всех воображаемых мирах такая же, как и в нашем мире. Таким образом, во всех возможных мирах 1+1 должно равняться 2, в любом мире должно быть бесконечно много простых чисел, прямые углы должны быть конгруэнтны и, разумеется, через точку, лежащую вне прямой должна проходить только одна прямая, параллельная данной.
Минуточку! Последнее — постулат параллельности, и утверждать, что он универсален, было бы ошибкой, как мы только что показали. Если бы постулат параллельности был верен во всех воображаемых мирах, то неэвклидова геометрия была бы невозможна! Это отбрасывает нас назад, в ту же ситуацию, в которой находились Саккери и Ламберт — безусловно, не лучший выход! Что же, если не математика, является общим для всех воображаемых миров? Может быть, логика? Или и она тоже находится «под подозрением»? Могут ли существовать миры, в которых противоречия — нормальное и обыденное явление, миры, где противоречия не являются противоречиями?
В каком-то смысле уже лишь потому, что мы изобрели подобное понятие, такие миры, действительно возможны — однако в более глубоком смысле они также весьма невероятны (Что уже само по себе маленькое противоречие). Говоря серьезно, если мы хотим хоть как-то общаться, то, по видимости, нам придется установить некую общую базу, включающую логику. (Существуют системы верований, отрицающие подобную точку зрения за то, что она слишком логична. В частности, дзен-буддизм с одинаковой готовностью принимает как противоречия, так и непротиворечия Это может показаться непоследовательным, но непоследовательность — органическая часть дзен-буддизма, ну что тут можно сказать?)
Является ли теория чисел одинаковой во всех возможных мирах?
Если мы допустим, что именно логика — одна и та же во всех возможных мирах (заметьте, что мы еще не определили, что такое логика — определение будет дано в последующих главах), будет ли этого достаточно? Возможно ли, что в каких-то мирах количество простых чисел не бесконечно? Не должны ли числа подчиняться одним и тем же законам во всех возможных мирах? Или же лучше вообще считать число неопределяемым понятием, как «ТОЧКА» или «ЛИНИЯ»? В этом случае, теория чисел раздвоилась бы, подобно геометрии, на стандартную и нестандартную. Тогда должно было бы существовать соответствие абсолютной геометрии, некая центральная теория, общая для всех теорий чисел, отличающая их, скажем, от теорий какао, бананов или резины. Большинство современных математиков считают, что такая центральная теория чисел существует — вкупе с логикой она является необходимой частью всех возможных миров. Эта сердцевина теории чисел, соответствующая абсолютной геометрии, называется арифметика Пеано, ее определение будет дано в главе VIII. Также уже точно установлено, что теория чисел действительно разветвляется на стандартную и нестандартные версии. (Это прямое следствие Теоремы Гёделя.) В отличие от ситуации с геометрией, однако, количество «сортов» теории чисел бесконечно, что делает положение с ней значительно более сложным.
Для практических целей все теории чисел одинаковы. Иными словами, если бы конструкция мостов зависела бы от теории чисел (и в каком-то смысле так оно и есть), было бы совершенно неважно, что существует множество ее вариантов — в аспектах, касающихся реального мира, все теории чисел совпадают. Этого нельзя сказать о различных геометриях; например, сумма углов в треугольнике равняется 180 градусам только в эвклидовой геометрии, она больше в эллиптической геометрии и меньше — в гиперболической. Говорят, что однажды Гаусс попытался измерить сумму углов в огромном треугольнике, образованном вершинами трех гор, чтобы раз и навсегда определить, какой именно тип геометрии управляет нашей вселенной. Через сто лет Эйнштейн открыл теорию (общую теорию относительности), утверждающую, что геометрия вселенной определяется количеством материи, в ней содержащейся — таким образом, никакой тип геометрии не присущ пространству как таковому. Это значит, что на вопрос «какой тип геометрии является истинным?» природа дает двусмысленный ответ не только в математике, но и в физике. А как же насчет соответственного вопроса «какой тип теории чисел истинен?»? Мы вернемся к нему после детального разбора Теоремы Гёделя.
Полнота
Если непротиворечивость — это минимальное условие, при котором символы приобретают пассивные значения, то ее дополнение, полнота — максимальное признание этих пассивных значений. Непротиворечивость означает, что «все, что производит система, истинно»; полнота же, наоборот, утверждает, что «все истинные утверждения производятся данной системой». Точнее, мы не имеем в виду все истинные утверждения в мире, а только находящиеся в области, которую мы пытаемся воспроизвести в данной системе. Таким образом, более точное определение полноты следующее: «Каждое истинное утверждение, которое может быть выражено в нотации данной системы, является теоремой.»
Непротиворечивость: когда каждая теорема, будучи интерпретирована, оказывается истинной (в каком-либо из возможных миров).
Полнота: когда все утверждения, которые истинны (в каком-либо из возможных миров) и выразимы в виде правильно сформированных строчек системы, являются теоремами.
Пример формальной системы, полной на своем скромном уровне — наша система pr в ее первоначальной интерпретации. Все правильные суммы двух положительных целых чисел представлены теоремами данной системы. Можно сказать то же самое по-другому: «Все правильные суммы двух положительных целых чисел доказуемы в данной системе.» (Внимание: используя термин «доказуемые утверждения» вместо термина «теоремы», мы начинаем стирать границу между формальными системами и их интерпретациями. Это не страшно, если мы четко осознаем этот факт, а также то, что некоторые системы допускают множественные интерпретации.) Система pr в первоначальной интерпретации полна; она также непротиворечива, поскольку не содержит таких ложных утверждений, которые были бы — используем наш новый термин — доказуемы внутри системы.
Некоторые читатели могут возразить, что система вовсе не полна, так как она не включает сложения трех положительных целых чисел (например, 2+3+4=9), хотя оно и может быть записано в нотации системы (--p---p----r---------). Однако эта строчка не является хорошо сформированной и поэтому должна считаться такой же бессмысленной как и prp---rpr. Тройное сложение просто не может быть выражено в данной системе, поэтому полнота системы сохраняется.
Несмотря на полноту системы pr в данной интерпретации, эта система, безусловна, далека от того, чтобы полностью выразить понятие истины в теории чисел. Она, например, не может сказать нам, сколько всего простых чисел. Теорема Гёделя о неполноте говорит, что любая «достаточно мощная» система уже в силу своей мощности является неполной, в том смысле, что имеются хорошо сформированные строчки, которые выражают истинные утверждения теории чисел, не являясь при этом теоремами. (Иными словами, в теории чисел имеются истинные утверждения, не доказуемые внутри самой системы.) Системы типа pr, полные но не очень мощные, напоминают патефоны низкого качества — мы сразу видим, что они настолько несовершенны, что никак не могут сделать то, чего бы нам от них хотелось — а именно, сказать нам все о теории чисел.
Как интерпретация может создать или разрушить полноту
Что означает выражение, употребленное мною выше, что «полнота — это максимальное подтверждение пассивных значений»? Оно означает, что если система непротиворечива, но не полна, то существует несоответствие между символами системы и их интерпретациями. Система недостаточно мощна, чтобы оправдать данную интерпретацию. Иногда, если интерпретации немного «подправить», система может стать полной. Для иллюстрации этой идеи давайте взглянем на модифицированную систему pr (включая схему аксиом II) и на выбранную нами интерпретацию.
Изменив систему pr, мы изменили также и интерпретацию символа r с «больше» на «больше или равняется». Мы нашли, что измененная система pr в такой интерпретации непротиворечива; однако в новой интерпретации есть что-то сомнительное. Проблема весьма проста: теперь имеется множество истинных утверждений, не являющихся теоремами. Например, «2 + 3 больше или равняется 1» выражено не-теоремой --p---r-. Просто эта интерпретация слишком небрежна! Она не отражает того, что делают теоремы системы. В такой неряшливой интерпретации система pr неполна. Мы могли бы поправить дело одним из двух способов: (1) прибавив к системе новые правила и, таким образом, сделав ее более мощной и (2) заменив интерпретацию на более аккуратную. В данном случае, заменить интерпретацию кажется более разумной альтернативой. Вместо того, чтобы интерпретировать r как «больше или равняется», мы должны сказать «равняется или больше на 1». После такой модификации система pr становится как непротиворечивой, так и полной. И эта полнота подтверждает правильность нашей интерпретации.
Неполнота формализованной теории чисел
В теории чисел мы снова встретимся с неполнотой; но в этом случае, чтобы исправить ситуацию, нам придется пойти в другом направлении — сделать систему более мощной путем прибавления новых правил. Ирония здесь заключается в том, что каждый раз, когда мы прибавляем новое правило, мы думаем, что уж теперь-то система станет полной! Эта дилемма может быть проиллюстрирована с помощью следующей аллегории.
Представьте себе, что у вас есть патефон и пластинка, которой мы пока дадим пробное название «Канон на тему В-А-С-H». Однако, когда мы проигрываем запись на нашем патефоне, вибрации, производимые записью, создают сильные помехи, мешающие нам узнать мелодию. Следовательно, заключаем мы, что-то должно быть не в порядке — или пластинка, или наш патефон. Чтобы проверить качество пластинки, мы должны прослушать ее на патефоне товарища; а чтобы проверить качество патефона, нам придется проигрывать на нем пластинки товарища, и смотреть, соответствует ли музыка этикеткам на них. Если наш патефон выдержит экзамен, тогда мы заключим, что дефект был в пластинке; с другой стороны, если пластинка пройдет свое испытание, то мы решим, что дефект — в нашем патефоне. Однако каково будет наше заключение, если тест выдержат оба? Вспомните цепь двух изоморфизмов (рис. 20) и подумайте над ответом!
Назад: Акростиконтрапунктус
Дальше: Маленький гармонический лабиринт

