Книга: Камень ломает ножницы. Как перехитрить кого угодно: практическое руководство
Назад: 11 Как распознать фальшивые числа
Дальше: 13 Как распознать финансовые пирамиды
12
Как распознать числа, которыми манипулировали
Один нью-йоркский страховой агент (фирма щедро оплачивала ему представительские расходы) оказался талантливым мошенником. Желая перейти на безбумажную документацию, его компания требовала сканы выписанных квитанций, а не сами квитанции. Страховой агент обнаружил: можно черной ручкой переправить в документе 1 на 7 или на 9, и на сканере с низким разрешением такое изменение незаметно.
Затем он пошел еще дальше и стал следить за тем, чтобы суммы, указанные в квитанциях, начинались с 1. Страховой агент мог позавтракать за 18 долларов и останавливаться в гостинице, где номер стоил 178 долларов. После этого он подправлял суммы и получал возмещение в размере 98 долларов за завтрак или 778 за гостиницу.
Одним росчерком пера он увеличил суточные расходы с 70 до 800. Но ему не повезло – аудиторский отдел страховой компании был одним из первых, применявших для анализа закон Бенфорда. В данном случае оказалось достаточно первых цифр, чтобы вызвать подозрения. Обнаружилось преобладание семерок и девяток и недостаток единиц. Расследование подтвердило факт обмана, и компания подала на страхового агента в суд, потребовав возмещения ущерба.
Подвергшиеся манипуляции числа могут представлять бо́льшую проблему, чем полностью выдуманные. В данном случае манипуляция означает, что кто-то ради личной выгоды уменьшил или увеличил реальную цифру. Изменение не обязательно должно быть таким грубым, как переправка 1 на 7. Зачастую достаточно достичь какого-то предела, цели или порога. Средства на представительские расходы обычно ограничены, при превышении либо не возмещаются суммы, либо требуются дополнительное подтверждение или документы. Можно ожидать, что предъявленные к возмещению цифры сосредоточатся чуть ниже границы.
«Это обычная практика для государственных чиновников», – заметил Марк Нигрини. Он изучил одно правительственное агентство. В нем сотрудникам выдавались закупочные карточки на сумму до 2500 долларов. Результат: «масса закупок на сумму 2500, 2499, 2496 долларов… Очевидно, это гениальные люди, которые говорили: “Не пишите 2501, пишите 2496 долларов. Я единственный из 35 000 правительственных чиновников знаю арифметику!” Однако все мы склонны думать как все, и поэтому каждый считает себя единственным».
Один из способов выявить исправления – проверка второй цифры. Сосчитайте, сколько раз каждая из десяти цифр встречается во втором знаке числа, справа от первой цифры. Для 74991 доллара вторая цифра – 4, и именно ее нужно учитывать при подсчете. Изобразите результаты в виде гистограммы.
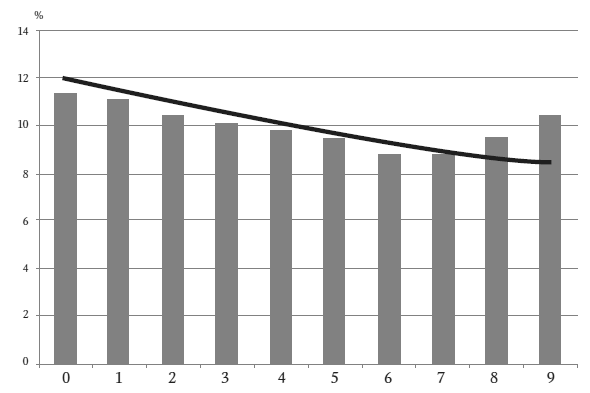
Вторые цифры: числа, подвергшиеся манипуляции
С реальными числами не следует ожидать слишком большой вариации в частоте вторых цифр. Закон Бенфорда предсказывает, что самой распространенной второй цифрой будет 0, с частотой появления 12 процентов, а реже всего должна встречаться 9 – в 8,5 процента случаев. Однако зачастую вы видите такую диаграмму, как представлена на рисунке на следующей странице. Сплошная линия – это идеальная кривая Бенфорда для вторых цифр, а столбики – реальные результаты подсчета. На первый взгляд разница не очень велика, однако она существенна. В столбиках показан избыток цифр 8 и 9, а также нехватка всех остальных. Это может произойти при «круглом» лимите, например, 1000 долларов. Обычно люди указывают расходы, немного не дотягивающие до порога.
Эффект порога – довольно распространенное явление, но не стоит делать поспешных выводов, когда вы сталкиваетесь с чем-то подобным. Наемный работник, знающий, что компания оплачивает расходы на еду до 50 долларов, может попробовать питаться на 49 с мелочью. Он не делает компании одолжение, а просто играет по установленным правилам.
С другой стороны, работник, преувеличивший расходы на еду – или фальсифицирущий их, – тоже имеет все основания не превышать установленного порога. Получив такие результаты, вы, возможно, захотите проверить поведение сотрудника – либо он представляет к оплате чеки, не превышающие порога, либо не переходит установленные границы, либо тут есть признаки подделки.
Иногда установленные пороги оканчиваются цифрой 5, например, 25 долларов. В таком случае на манипуляцию может указывать избыток троек и четверок во второй цифре.
Кевин Лоуренс приходил к инвесторам с беспроигрышным бизнес-планом. Его компания под названием Health Maintenance Centers (HMC) разрабатывала электронное оборудование и программное обеспечение для оздоровительных клубов: благодаря аппаратуре проще следить за состоянием клиентов на тренажерах. Это превратило бы каждое занятие в стрессовый тест, позволяя тренеру или врачу регулировать нагрузки и режим тренировок. Лоуренс продал акции и ценные бумаги HMC на сумму 74 миллиона долларов 5000 инвесторам по всей стране.
17 января 2002 г. Комиссия по ценным бумагам и биржам подала иск против Лоуренса и HMC, обвинив в мошенничестве в инвестиционной сфере. Обещанное IPO так и не состоялось. Вместо этого принадлежавшие инвесторам 163 миллиона долларов ушли к Лоуренсу и его подельникам. Комиссия обвиняла Лоуренса, что он потратил 2,1 миллиона долларов на 23 роскошных автомобиля, 1 миллион долларов на яхты 1,7 – на недвижимость и драгоценности, в том числе на обручальное кольцо стоимостью 330 тысяч долларов для Стейси Грей, еще одной обвиняемой.
Вероятно, Лоуренс не собирался мошенничать. Просто он принадлежал к тому типу предпринимателей, у которых привлекать деньги получается лучше, чем вкладывать их в успешные проекты, – его можно сравнить не с Берни Мэдоффом, а скорее с Максом Бялыстоком . Числа в бухгалтерской документации HMC отражали реальные операции. Но результаты некоторых цифровых тестов выглядели в высшей степени подозрительно. К сожалению, тесты провели только после того, как проблемы HMC получили огласку (органы судебно-бухгалтерской экспертизы г. Лейк-Освего, и независимо от них Марк Нигрини). Если бы инвесторы HMC проанализировали распределение цифр раньше, то могли бы сохранить деньги и избежать ущерба.
В гистограмме вторых цифр платежей компании HMC (см. следующую страницу) цифры 0 и 5 встречаются гораздо чаще, чем в кривой Бенфорда. Цифра 9 игнорировалась и встречалась значительно реже, чем 8. Это указывает, что кто-то часто использует круглые числа, такие как 10 (всего 459 раз), 15 000 (122 раза) или 1 000 000 долларов (4 раза). HMC часто оперировала круглыми числами.
Точно так же поступают колумбийские наркокартели и бабушки, выписывающие чек внукам на день рождения. Круглые цифры не обязательно должны вызывать подозрение. Вы идете к банкомату и снимаете со счета круглую сумму, например, 300 долларов. Вы не знаете, на что потратите деньги, и поэтому просто выбираете сумму из предложенных на сенсорном экране вариантов круглых чисел. Когда мы придумываем денежные суммы, не пытаясь никого обмануть и делая их похожими на случайные, то почти всегда выбираем круглые числа.
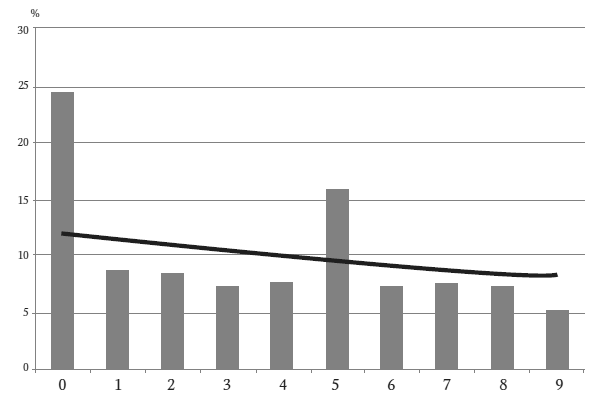
Вторые цифры: Health Maintenance Centers
Единственное, что отличает круглые числа от остальных – в некоторых обстоятельствах они не похожи на реально бывающие в бизнесе. Компании обязаны торговаться за наиболее выгодное соглашение и не покупать больше, чем необходимо. Даже если цены представляют собой круглые числа, броуновское движение скидок, льгот, транспортных расходов и налогов делают подавляющее большинство цен некруглыми. Наука честного ведения дел излучает гравитационное поле, подтягиваюее величины, выраженные в долларах, к кривой Бенсона. Когда с деньгами обращаются небрежно или пытаются что-то скрыть, долларовые величины имеют тенденцию отклоняться от идеала.
Руководители HMC пользовались средствами компании как личными чековыми счетами. Или банкоматом. Выяснилось, что 111 платежей HMC составляли 301,50 доллара. Сотрудникам выдали банковские карты с доступом к счетам компании. Лимит снятия наличности составлял 300, и банк брал комиссионные в размере 1,50.
Большое количество таких выплат, как 10, 15, 20 и 25 долларов, объяснялось банковской комиссией за выдачу наличных по чекам за телеграфные переводы. Эти услуги предназначены для частных клиентов. У компаний есть более дешевые способы перемещения денежных потоков. В лучшем случае это указывает, что сотрудники HMC не были заинтересованы в экономии средств инвесторов. Кроме того, возникает вопрос, почему собственные чеки HMC были недостаточно хороши?
Ответ тоже дают числа. Еще одно подтверждение дала банковская комиссия.
Расследование показало, что HMC использовала чеки и переводы, чтобы перемещать большие круглые суммы от одной сомнительной организации в другую, и в конечном итоге большая часть этих денег оседала в карманах руководителей компании. Финансовое мошенничество, вероятно, должно было затруднить понимание происходящего.
На протяжении пяти лет до краха энергетическая компания Enron, печально знаменитая своим мошенничеством, публиковала следующие данные о доходах:
1996 – 13 289 миллиардов долларов1997 – 20 273 миллиардов долларов1998 – 31 260 миллиардов долларов1999 – 40 112 миллиардов долларов2000 – 100 789 миллиардов долларов
Задним числом мы знаем, что эти числа фиктивны, и сочинил их финансовый директор компании Эндрю Фастоу. Руководство Enron попало под гипноз прямой зависимости между доходом и стоимостью акций. Цена на акции компании вывешивалась даже в лифте. Фастоу нашел способ сообщать о доходах, подтверждавших ту цену, которую все хотели видеть.
Президент Enron Джеффри Скиллинг большую часть рабочего дня тратил на переубеждение последователей «Фомы неверующего». На конференции по телефону, впоследствии ставшей знаменитой, Ричард Грабман, аналитик компании Highfields Capital, заметил: Enron – единственная среди известных ему компаний, не публикующая бухгалтерский баланс или отчет о движении денежных потоков вместе с данными о доходах. «Да, большое спасибо, – ответил Скиллинг. – Мы ценим ваше замечание… козел!»
Немногие данные, опубликованные компанией Enron, выглядели подозрительно. Когда компания намеревается продать миллион устройств, то результат 998 300 неудовлетворительный. Три из пяти сумм, указанных как доход, лишь немного превышали психологически значимые круглые числа – 20, 40 и 100 миллиардов долларов.
Каждая из превышающих порог сумм имеет вторую цифру 0. Закон Бенфорда предсказывает, что вероятность появления 0 в качестве второй цифры составляет 11,97 процента. Если вы имеете дело с несколькими числами, немного превышающими порог, эта вероятность уменьшается. Шансы на то, что три из пяти чисел будут иметь второй цифрой 0, составляют 1 из 75.
Доход – самый яркий показатель, обычно упоминаемый в СМИ. Подобных показателей не так много, однако именно они влияют на цену акций. Еще одна часто цитируемая цифра – прибыль на акцию. Вот как она выглядит у компании Enron:
1996 – 1,08 доллара1997 – 0,16 доллара1998 – 1,01 доллара1999 – 1,10 доллара2000 – 1,12 доллара
Прибыль на акцию впечатляет гораздо меньше, чем доход компании. В Enron стремились поддерживать ее выше одного доллара за акцию, и данные за пять лет показывают небольшой рост. Из общего тренда выбивался 1997 г. В объяснении указывалось, что доход до выплаты налогов и процентов составлял 0,87 доллара на акцию, но «факторы, влияющие на сопоставимость» уменьшили его до 0,16 доллара. Творческий подход к бухгалтерии позволил Enron собрать расходы и снижение цен в одну большую кучу – ужасный 1997 год – и сохранить для остальных годов прибыль на акцию выше одного доллара.
Идея Enron состояла в том, что значение имеет доход компании, а не прибыль на акцию. Доходом легче манипулировать. В начале 2001 г. сотрудники Enron снова заговорили об удвоении дохода до красивого круглого числа, 200 миллиардов долларов. Осуществлению великолепного плана помешали длительные сроки тюремного заключения, а именно к ним приговорили руководителей компании.
Так поступали не только в Enron. В проведенных позже исследованиях анализировались вторые цифры опубликованных доходов или прибыли всех крупных американских корпораций. Компаний много, они разной величины, в самых разных отраслях, а значит, опубликованные числа должны довольно точно соответствовать закону Бенфорда. Так и оказалось – за исключением вторых цифр 0 и 9. Нулей было больше, а девяток меньше ожидаемого.
Назовем это аномалией Enron. Вместо того чтобы показать прибыль в размере 99 центов на акцию, компании находят способы сделать так, чтобы она превысила 1 доллар. Исследования совокупных данных не позволяют определить, какие именно корпорации лукавят, но их доля должна быть существенной.
Присутствует также небольшая аномалия для второй цифры 5. 24 цента на акцию компании обычно округляют до 25.
Нигрини отмечает, что в данных об убытках наблюдается противоположная тенденция. Самая большая сумма убытков, о которой сообщили американские корпорации, составила 99 280 миллионов долларов.
Это число взято из формы 10-К компании American International Group (AIG) за 2008 г.
Теперь посмотрим на вторые по величине убытки американских корпораций:
99 696 миллионов долларов
Это убытки компании AOL TimeWarner’s за 2002 г. Замечаете сходство? Самые большие убытки американских корпораций выглядят как цены в магазине, где все товары продаются по 99 центов.
С учетом того, что крупные и предположительно уважаемые корпорации имеют тенденцию выбирать психологически более комфортную сторону круглых чисел, можно представить, насколько хуже обстоят дела в стартапах и развивающихся компаниях. Банкам, венчурным капиталистам и инвесторам часто нужно сформировать представление о кредитоспособности компании из ограниченного объема данных. Значимыми показателями могут быть не только доход или выручка, но также количество проданного товара, число загрузок или кликов. Эти показатели могут публиковаться поквартально, ежемесячно, еженедельно или ежедневно. Но независимо от системы измерения наблюдается тенденция превышения значимых порогов.
Эффективный тест на реальность данных – проверить вторые цифры на избыток 0. Сколько чисел, едва превышающих важный порог, считать подозрительными? Первым делом сосчитаем, сколько значимых показателей вам предоставили. Обозначим это число как N. Затем сосчитаем, в скольких из этих чисел вторая цифра 0. Обозначим это число Z.
Откроем таблицу. Вам потребуется использовать так называемую функцию биномиального распределения. Знать, что это такое, вовсе не обязательно. Эта функция встроена в Excel или в любую совместимую финансовую программу. Наберите в ячейке Excel:
=1-BINOM.DIST (Z-1, N, 0,1197, TRUE)
Введите числа или ссылки на содержащие их ячейки для Z и N. Программа рассчитает вероятность того, что в списке из N чисел окажется Z нулей в качестве второй цифры.
Пример. Допустим, в начале 2001 г. вы задумались о покупке компании Enron, и ее руководство предоставило вам десять приведенных выше цифр – доход компании и прибыль на одну акцию в течение пяти лет. Тогда N будет равняться 10, а Z — 5.
Вычтем 1 из Z и полученное число 4 вставим на место первого аргумента функции. Значение второго аргумента будет 10, а третий аргумент – вероятность, согласно закону Бенфорда, что вторая цифра будет 0, то есть 0,1197. По поводу аргумента «TRUE» волноваться не следует – просто напечатайте его.
Результат вычислений – 0,368 процента, или 1 из 272. Это значит, есть серьезные основания подозревать, что компания Enron просто завысила все эти важные показатели, выбирая их случайно.
Какая вероятность заставит вас отказаться от покупки? Ни один статистик вам этого не скажет. Происходят и совпадения. Для венчурного капиталиста цель не в обеспечении точности финансовых показателей, а в том, чтобы доказать благонадежность и установить комфортный уровень.
Сравним. При испытаниях нового лекарства для публикации в медицинском журнале обычно требуется уровень уверенности 1 из 20 (5 процентов). Исследователю нужно показать: вероятность того, что наблюдаемый эффект случаен, не превышает 5 процентов.
Критерий 5 процентов произволен. Он не должен иметь какого-либо значения для бизнеса. Тем не менее, вы можете выбрать его как отправную точку для принятия решения. Если шансы меньше 5 процентов, считайте это предупреждением. В таком случае следует запросить дополнительные данные.
Повторите процесс с новыми числами, проведя расчеты для изменившихся N и Z. Снова вероятность меньше 5 процентов? Это немного напоминает оценку нового ресторана. Вы идете туда один раз и остаетесь недовольны – но возможно, у шеф-повара просто был неудачный день. Посетите ресторан несколько раз, и вы получите более точное представление об истинном положении дел.
Означает ли высокая доля нулей в качестве второй цифры, что компания завышает показатели? Стоит ли иметь с ней дело? Решать вам. Но есть вероятность, что она не совсем честна.
В 1980-х и 1990-х гг. налогоплательщики больше всего боялись аудиторских проверок Налогового управления США, выполнявшихся под эгидой Национальной исследовательской программы (NRP). Генератор случайных чисел выбирал девятизначный номер. «Счастливый» обладатель карточки социального страхования с этим номером подвергался доскональному аудиту и должен был представить документы, подтверждающие каждую запись в налоговой декларации. Проверка случайно выбранного налогоплательщика и анализ всех данных позволили Налоговому управлению понять, какие строчки декларации подделываются чаще всего. С научной точки зрения все было идеально – но не с политической. Многие налогоплательщики выражали недовольство, и в середине 1990-х конгресс вынудил Налоговое управление свернуть NRP.
После закрытия программы налоговые органы сосредоточились на аналитике. Мало кто сомневался, что анализ данных использует закон Бенфорда, однако не склонное к откровенности Налоговое управление этого не подтверждало. Тем не менее, еще в 1998 г. газета New York Times сообщала: «Налоговые органы нескольких государств и нескольких американских штатов, включая Калифорнию, для проверок крупных компаний и финансовых фирм используют программное обеспечение на основе закона Бенфорда».
Макс Нигрини занимался этим задолго до сборщиков налогов. В одном из первых исследований налоговых деклараций США он проанализировал такие записи, как процентный доход и выплаты по ипотеке, благотворительные взносы, доходы от прироста капитала и расходы малого бизнеса, подпадающие в «раздел С». Они значительно отличались от распределения Бенфорда. Больше всего подозрений вызывали арендная плата и административные расходы малого бизнеса из раздела С.
Нигрини обнаружил: незадокументированные расходы налогоплательщиков с низким доходом выглядят подозрительнее, чем у налогоплательщиков с высоким доходом. Небогатые люди знают, что риск проверки для них невелик, и поэтому чаще фальсифицируют данные. С другой стороны, богатые имеют возможность нанять профессионалов для составления финансовых отчетов, и те их убедят не делать глупостей.
Парадокс в том, что Нигрини не мог сказать, какие именно декларации неточны. Малый бизнес по большей части сообщает всего одну сумму в качестве арендной платы. Какие-то из этих чисел реальные, а какие-то преувеличены. И только массив из многих тысяч сумм аренды заставил заподозрить мошенничество.
Открытия Нигрини необыкновенно полезны для налоговых органов, причем не только потому, что указывают на строки налоговой декларации и типы доходов, требующие особого внимания, но и при составлении инструкций и изменении законодательства. В настоящее время Налоговая служба США требует от ипотечных заимодателей сообщать о процентных ставках в форме 1098, а проценты по потребительскому кредиту больше вообще не рассчитываются. С 2011 г. биржевые маклеры, а с 2012 г. паевые инвестиционные фонды обязаны сообщать в налоговые органы базовую стоимость ценных бумаг В 2012 г. Налоговое управление провело выборочные проверки лиц с высоким движением наличности.
Несколько лет назад Управление налоговых сборов Великобритании применило цифровые тесты к британским налоговым декларациям и выяснило: у владельцев малого бизнеса в суммах продаж слишком часто встречаются две первые цифры 14. Причина очевидна – в то время британское законодательство позволяло малому бизнесу пользоваться упрощенной формой отчетности, если сумма продаж не превышала 15 тысяч фунтов стерлингов. С тех пор этот порог поднимался несколько раз. И каждый раз вместе с ними на новый уровень поднимались манипуляции.
Для расчета федерального подоходного налога американские налогоплательщики со средним доходом используют налоговую таблицу. Эти таблицы составлены с шагом 50 долларов. В 2011 г. не состоящий в браке человек с облагаемым налогом годовым доходом 71 049 долларов должен был заплатить подоходный налог в размере 13 894 долларов. Но если он заработал на один доллар больше (71 050), то его доход попадал в другую строчку таблицы, и сумма налога увеличивалась на 12 долларов (13 906).
Вы, наверное, подумаете, что никто не станет мошенничать с налоговой декларацией из-за 12 долларов. Нигрини проанализировал две последние цифры сумм облагаемого налогом дохода и обнаружил свидетельства, что при заполнении декларации налогоплательщики подправляли суммы дохода, чтобы они оказывались чуть ниже границы. Слишком много чисел оканчивались на 48 или 49, 98 или 99. А количество сумм дохода, немного превышавших границу (оканчивавшихся на 50 или 51, 00 или 01) было меньше ожидаемого.
Чтобы доказать сознательное уклонение от налогов, Нигрини сравнил налогоплательщиков, пользовавшихся налоговыми таблицами, с теми, которые должны умножать облагаемый налогом доход на предельную налоговую ставку. Во втором случае в числах не обнаружилось никаких признаков манипуляции.
Облагаемый налогом доход вычисляется из других записей декларации, и его невозможно изменить – в противном случае появится математическая ошибка. Налогоплательщик, слега превысивший порог, должен вернуться назад и найти способ прибавить пару долларов к вычетам или на несколько долларов сократить поступления. В самом невинном случае это может указывать на налогоплательщика с остро отточенным карандашом в руке: он порылся в памяти и обнаружил там забытый налоговый вычет. Менее оптимистичный вариант – налогоплательщик не откажется от мелкого мошенничества, если шанс быть пойманным невелик.
Формула аудита для Налоговой службы США генерируется при помощи прогнозной аналитики. Статистические корреляции позволяют предсказать, какие налоговые декларации имеют наибольшую вероятность оказаться нечестными и поэтому заслуживают дополнительной проверки. В компьютерах Налоговой службы США хранятся все налоговые декларации, и не приходится сомневаться, что эта информация используется должным образом. То, что в этом году ваш облагаемый налогом доход оказался на доллар меньше порогового значения, может быть совпадением. Но если за последние десять лет сумма слегка не дотягивает до …00 или …50, это уже не совпадение.
Эффект порога позволяет выполнить очень простой тест на честность. И вполне возможно, что такой тест присутствует в процедуре аудита. Дело не в том, что налоговые органы волнуются из-за нескольких долларов. Но если налогоплательщик постоянно жульничает с налоговой сеткой и в его декларации присутствуют другие настораживающие признаки, такие как расходы малого бизнеса, подпадающие в «раздел С», или крупные пожертвования на благотворительность, это вызывает подозрение.
Поэтому лучше быть кристально честным в мелочах. Машина для предсказаний наблюдает за вами и знает больше, чем вы думаете.
Политическая блогосфера с огромным энтузиазмом восприняла закон Бенфорда. Он приобрел репутацию волшебного черного ящика: для выявления мошенничества на выборах требуются лишь результаты подсчета голосов на избирательных участках, доступные любому блогеру, сидящему в гостиной у матери. Результатом стало растущее количество заявлений о подтасовках. Обвинения в украденной победе, пересыпанные жаргоном статистиков (а его почти никто не понимает), были подхвачены журналистами (а им следовало бы проявить больше ответственности). В интернете ошибки можно опровергнуть, но не стереть. А еще нужно учитывать, что существует новая теория заговора, и у нее имеются приверженцы.
Подавляющее большинство заявлений такого рода основаны только на проверке первых цифр. Такой тест никогда не бывает окончательным, а в некоторых случаях вообще ничего не значит. Необходимо сравнивать тенденции, проявившиеся на этих выборах, с теми, что наблюдались на предыдущих. Это делается редко.
Фанатичные блогеры также занимаются «добычей данных». На федеральных выборах и выборах штатов избиратели голосуют на нескольких тысячах участков. Проверьте достаточно большое количество участков, и вы обязательно наткнетесь на те, где статистика выглядит подозрительно. Они не подозрительны, если смотреть на общую картину, но именно общая картина ускользает от внимания фанатиков.
Идею проверки выборов посредством анализа цифр приписывают Александру Собянину. Он изучил коррупционные парламентские выборы 1993 г. в России, получившие печальную известность. Собянин предложил несколько статистических тестов. Один из них основывался на законе Бенфорда и все строились на допущении, что придуманные числа будут отличаться от аутентичных. Собянин утверждал: проверка выборов 1993 г. выявила подтасовки. Вывод этот по меньшей мере неопровержим. За этим последовали и другие подобные заявления. После выборов 2009 г. в Иране, когда президентом на второй срок был избран Махмуд Ахмадинеджад, Нигрини проанализировал результаты по участкам и обнаружил свидетельства фальсификации.
Недавняя статья Джозефа Декерта, Михаила Мягкова и Питера С. Ордешука называется «Неприменимость закона Бенфорда для выявления мошенничества на выборах» (The Irrelevance of Benford’s Law for Detecting Fraud in Elections). Авторы предупреждают, что у нас нет достаточного количества исследований, показывающих, насколько хорошо результаты честных выборов согласуются с законом Бенфорда. Один из неизвестных факторов – разница в размерах округов. Обычно предполагается, что избирательные комиссии делают округа приблизительно равными, избегая существенных различий. Если только нет тайных причин для манипуляций избирательными участками… Кто знает?
Представьте себе сельскую местность в штате Айова, где избирательные участки одинаковые – по 5000 избирателей на каждом. Это консервативный регион, предпочитающий Митта Ромни Бараку Обаме в соотношении 70 на 30 процентов. Ромни набирает в среднем 3500 голосов на каждом участке, а Обама 1500 – с небольшими вариациями. Первые цифры количества голосов на участке у Ромни будут 3, а у Обамы 1. Волшебный черный ящик зажигает красный сигнал! Но все в порядке. Просто мы анализируем регион, где распределение участков и политических предпочтений ровное, как кукурузное поле.
В этой ситуации результаты обоих кандидатов могут вызвать ложную тревогу. Еще большее беспокойство вызывают случаи, когда подозрения связаны только с одним из кандидатов. Довольно часто какой-либо кандидат в городских районах пользуется большей популярностью, чем в сельских (или наоборот). В таких ситуациях результаты одного из кандидатов лучше согласуются с законом Бенфорда, чем у другого.
Чтобы использовать распределение цифр для выявления мошенничества на выборах, необходимо понимать, как происходит мошенничество. В некоторых странах коррумпированные аппаратчики садятся и придумывают числа, а затем выдают их за результаты голосования на участках. В российских выборах результаты на многих участках бесстыдно круглые (оканчиваются на 0) – без каких-либо попыток скрыть обман. «Разумеется, мошенничество было, – говорит Владимир Шевчук, член избирательной комиссии Татарстана, о российских выборах 2000 г., – но одна из его причин – неэффективный механизм подсчета бюллетеней… Чтобы соблюсти процедуру, требуется не одна ночь, а больше. Люди смертельно устают и поэтому прибегают к уловкам».
В Америке мошенники могут зарегистрировать избирателей, взяв фамилии с местного кладбища, и этими голосами заполнить избирательные урны в пользу своего кандидата, или просто «потерять» бюллетени, поданные за соперника. Суммарное воздействие большинства фальсификаций определяется умножением результатов кандидата на коэффициент, зависящий от того, сколько голосов, по мнению фальсификаторов, нужно для победы. Это сложно определить с помощью закона Бенфорда. Одно из свойств закона в том, что можно умножить весь массив данных на любой коэффициент, и при этом числа по-прежнему будут соответствовать распределению Бенфорда.
Для выявления сфальсифицированных общих результатов больше подходят тесты последних цифр. Хотя маловероятно, что придумывать числа будет один человек. Если целая армия нечестных сотрудников избирательных комиссий придумает по одному числу каждый, то групповой эффект нивелирует любые персональные особенности. Придется оперировать лишь относительно универсальными характеристиками придуманных чисел.
Анализируя выборы 2012 г. в Нигерии, Бернд Бербер и Александра Скакко предложили исследовать сдвоенные последние цифры (00, 11, 22… 99). Как мы уже видели, они реже всего встречаются среди придуманных чисел, и это обстоятельство может послужить сигналом, предупреждающим о необходимости дальнейшей проверки.
Трудность анализа цифровых результатов выборов в том, что фанатиков зачастую не интересуют поиски истины. Они хотят, чтобы любая аномалия воспринималась как неопровержимое доказательство нечестности. Если последующее расследование не выявляет мошенничества, они все равно могут заявить о фальсификации, опираясь только на анализ цифр. К таким заявлениям следует относиться скептически.
Любой анализ цифр основан на допущении, что «плохие парни» о нем не знают. Пока это верно, но когда-нибудь ситуация изменится.
В прошлом лишь немногие криминалисты знали об отпечатках пальцев. Теперь даже самые тупые взломщики пользуются резиновыми перчатками. Есть множество способов противостоять анализу цифр, и они не очень сложны.
Нигрини оптимистично предположил: распространение знаний о законе Бенфорда может стать средством устрашения, подобно знанию об отпечатках пальцев и анализе ДНК. Тот, кто решится на мошенничество, должен будет спланировать искажение данных, а затем скорректировать числа так, чтобы они соответствовали распределению Бенфорда. Это дополнительная работа. Кроме того, корректировка данных уменьшит степень фальсификации или потребует дополнительных действий, а они-то выдадут мошенника – или то и другое вместе.
Проблема в том, что преступников не так просто испугать – на то они и преступники. Такие люди плохо представляют отдаленные последствия своих действий. Это палка о двух концах. Все видели полицейские сериалы, однако криминалистические методы остаются эффективными, поскольку большинство преступлений совершаются под влиянием эмоций, без планирования. Это справедливо и для многих финансовых и электоральных преступлений. Растратчик начинает красть потому, что проигрывает в Лас-Вегасе. Предприниматель «улучшает» бухгалтерский баланс перед встречей с инвестором. Правящая партия начинает жульничать в последнюю минуту, когда выясняется, что проигрыш возможен.
При любом применении анализа цифр полезно задать себе вопрос: какова вероятность, что лицо, предоставляющее данные, знает о законе Бенфорда, предполагает, что числа могут быть подвергнуты криминалистическому анализу, и обладает достаточной математической подготовкой, чтобы принять контрмеры.
Резюме: Как распознать числа, которыми манипулировали
• Вторые цифры финансовых данных могут помочь в выявлении манипуляции. Переходя границу круглого числа, манипулятор в качестве второй цифры относительно часто выбирает 0 и относительно редко 9.
• Если цель – не превысить круглое число, манипулятор в качестве второй цифры относительно часто выбирает 9 и относительно редко 0. Такое часто встречается в затратах на представительские расходы.
• Сам по себе анализ цифр не может ничего «доказать». Его ценность состоит в том, что он выявляет данные, заслуживающие дополнительной проверки опытным аудитором. Следует скептически относиться к заявлениям (например, о фальсификациях на выборах), основанным на проверке первых цифр с помощью закона Бенфорда.

