Книга: Камень ломает ножницы. Как перехитрить кого угодно: практическое руководство
Назад: 10 Как интерпретировать рейтинги, полученные с помощью краудсорсинга
Дальше: 12 Как распознать числа, которыми манипулировали
11
Как распознать фальшивые числа
Марк Нигрини, выросший в южно-африканском Кейптауне, был очарован магией цифр. Он приехал на учебу в США, надеясь получить докторскую степень в области финансов. В апреле 1989 г. он учился в аспирантуре и подбирал тему для будущей диссертации. Однажды в университете Цинциннати он наткнулся на краткое упоминание закона Бенфорда. «В тот же вечер я отправился в библиотеку и взял статью Бенфорда», – вспоминал Нигрини. Знакомство с ней изменило всю его жизнь.
Физик Фрэнк Бенфорд в 1920-х гг. работал в компании General Electric в городе Скенектади. В то время для научных расчетов использовались таблицы логарифмов. Бенфорд заметил: первые страницы книжки с таблицами логарифмов истрепались от многократного использования, а последние выглядели почти новыми. Именно это случайное наблюдение, а не работа, за которую ему платила General Electric, послужило причиной того, что имя Бенфорда осталось в истории.
Числа, которые требовались Бенфорду, обычно начинались с маленьких величин, а именно они находятся в начале логарифмических таблиц. Так, например, Бенфорд обнаружил, что около 30 процентов чисел, с которыми имеют дело ученые и инженеры, начинаются с цифры 1. И только 5 процентов – с цифры 9. Поэтому последние страницы книги с таблицами логарифмов оставались практически нетронутыми.
Бенфорд рассказал об открытии химику Ирвингу Ленгмюру (будущему лауреату Нобелевской премии). Ленгмюр убедил его опубликовать статью на эту тему. Отличавшийся методичностью Бенфорд исследовал непонятную закономерность еще десять лет. Выяснилось, что она справедлива не только для научных расчетов. Бенфорд попытался проанализировать первые цифры бейсбольной статистики и обнаружил такое же распределение. Он выписал все числа, встречавшиеся в журнале Reader’s Digest. То же самое. Счет теннисных матчей, котировки на бирже, длина рек, атомные веса, счета за электричество на Соломоновых островах и числа, встречающиеся на первой странице New York Times – все подчинялось одной и той же закономерности. Похоже на теорию заговора. Все взаимосвязано.
Наконец, в 1938 г. Бенфорд опубликовал результаты в журнале Proceedings of the American Philosophical Society. В статье он привел точную формулу для вычисления пропорции чисел, начинающихся с каждой цифры. Вот они:
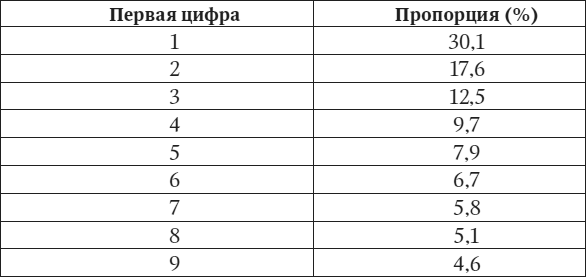
Вы можете спросить, почему здесь отсутствует цифра 0. Бенфорд анализировал только первые ненулевые цифры. Поэтому числа 7129600 и 0,000072002 начинаются с одной и той же цифры 7.
Формула Бенфорда также предсказывает распределение вторых, третьих и так далее цифр числа. В этих случаях уже присутствует 0. Однако преобладание низких величин здесь уже менее выражено. По этой причине выявленную Бенфордом закономерность иногда называют законом первой цифры.
Сам Бенфорд выбрал для статьи другое название, «Закон аномальных чисел» (The Law of Anomalous Numbers). В настоящее время он известен как закон Бенфорда. Как выяснилось, это несправедливо. Данное явление обнаружил (и опубликовал статью) другой, гораздо более известный ученый – астроном Саймон Ньюком. Его статья в номере журнала American Journal of Mathematics за 1881 г. начиналась с констатации факта: «То, что десять цифр встречаются с разной частотой, должно быть очевидно всякому, кто часто пользуется логарифмическими таблицами и замечает, насколько первые страницы истрепаны сильнее последних».
Мне кажется, это очередное доказательство того, как трудно придумать что-то свое и как часто остаются незамеченными даже оригинальные идеи. По какой-то причине о статье Ньюкома вскоре забыли, а статья Бенфорда получила поддержку. Одно из возможных объяснений в том, что статья Бенфорда «выехала» на знаменитой статье физика Ханса Бете, которая была помещена в журнале сразу же вслед за ней.
В настоящее время известно, что закон Бенфорда применим ко всем видам данных, которые не догадался проверить даже сам неутомимый автор. Известно также, что закон Бенфорда не применим ко многим числовым комбинациям (телефонные номера, обозначение возраста и веса, номера карточек социального страхования, коэффициенты умственного развития, победившие номера лотерейных розыгрышей и почтовые индексы). Примером может служить вес взрослых американцев. Совершенно очевидно, что 1 – самая распространенная первая цифра, ее доля гораздо выше, чем 30 процентов, предсказанных законом Бенфорда. Самая редкая – шестерка, даже реже, чем в распределении Бедфорда: немногие мужчины весят от 60 до 69 и от 600 до 699 фунтов.
Неприменим закон Бенфорда и к назначенным номерам, таким как номер телефона или карточки социального страхования. Тот, кто назначает номера, использует все или почти все возможные варианты. Номера, начинающиеся на 1, встречаются так же часто, как и те, которые начинаются с любой другой цифры.
Те, кто обладает математической интуицией, могут прийти к тому же выводу самостоятельно. Для всех остальных это неразрешимая загадка. Почему закон Бенфорда применим к номерам домов на улице, но не применим к почтовым кодам? Откуда в газете New York Times знают, будто числа, начинающиеся на 1, нужно упоминать в шесть раз чаще, чем те, которые начинаются на 9?
Закон Бенфорда справедлив для некоторых чисел, отражающих результаты измерений, например, городского населения или сумм, списанных с кредитных карт. Попробуем привести быстрое и интуитивное объяснение. Представьте, что вы положили на счет для инвестиционных операций 1000 долларов, которые удваиваются каждые десять лет. Первая цифра баланса вашего счета будет оставаться 1 на протяжении первых десяти лет. Сумма будет увеличиваться до 1100, 1200, 1300 долларов и так далее, до 1900, пока в конце первого десятилетия не достигнет 2000 долларов.
До следующего удвоения пройдет еще 10 лет. За это время сумма на счете постепенно увеличится с 2000 до 3000, а затем до 4000 долларов. Это значит, что на 2 и 3 в качестве первых цифр баланса счета приходится столько же времени, сколько на цифру 1.
В третьей декаде сумма на счете увеличится с $4000 до $8000, причем первыми цифрами будут 4, 5, 6 и 7. На протяжении четвертого десятилетия сумма увеличится до 16 000, и первыми цифрами сначала будут 8 и 9, а остальное время снова 1.
Итак, в сумме на инвестиционном счете 1 будет присутствовать больше времени, чем 2, 2 больше, чем 3, и так далее. Если выбрать случайный момент времени, то вероятность каждой из девяти цифр оказаться на первом месте будет точно соответствовать распределению Бенфорда.
В нашем мире есть множество вещей, от колоний микроорганизмов до социальных сетей, которые растут экспоненциально, хотя и не обязательно так занудно, как в моем примере. Но когда естественный рост рассеивает числа на несколько порядков величины, они приближаются к распределению Бенфорда. Если бы шимпанзе бросала дротик дартса в листок с финансовыми отчетами или ценами на бирже, то попадания с достаточной точностью соответствовали бы закону Бенфорда.
Закон Бенфорда напоминает, что числа – это искусственный способ отображения количественных соотношений в окружающем нас мире. Как писал сам Бенфорд, «в действительности это теория явлений и событий, а числа всего лишь играют незначительную роль безжизненных символов живого».
«Я подумал, что если предсказуемые закономерности для чисел действительно существуют, то аудиторы, наверное, смогут определить, какие данные соответствуют действительности, а какие вымышлены», – вспоминал Марк Нигрини.
Бухгалтеры и налоговые органы были бы рады иметь формулу для определения, какие цифры показаны честно, а какие нет. Нигрини быстро решил: его диссертация будет посвящена применению закона Бенфорда для выявления финансового мошенничества.
Он обнаружил, что после статьи Бенфорда на эту тему почти ничего не написано. Единственным, кто увидел практическую ценность открытия, оказался Хэл Вэриан (в настоящее время главный экономист Google). В 1972 г. Вэриан предложил использовать закон Бенфорда в качестве «индикатора чепухи». В политике решения основываются на сложных прогнозах издержек и выгод. Цифры в этих прогнозах должны соответствовать распределению Бенфорда, утверждал Вэриан. Если это не так, значит, составитель прогноза брал цифры с потолка или подгонял в соответствии со своими целями.
Вэриан не стал развивать эту идею – как и другие. Это подогрело энтузиазм Нигрини, но не его руководителя. «Он хотел бы, чтобы я был восьмидесятым ученым, исследовавшим этот вопрос», – объяснял Нигрини. Он настоял на теме диссертации, однако одобрение получил только после того, как написал две трети текста. Четыре месяца спустя работа была закончена.
Идея Вэриана и Нигрини может быть проиллюстрирована. Имея массив чисел, вы можете нарисовать столбиковую диаграмму (гистограмму), показывающую, сколько раз каждая цифра появляется первой. Просто сосчитайте, сколько чисел начинается с цифры 1, сколько с 2 или 3, и так далее. Для честных данных, подчиняющихся закону Бенфорда, диаграмма будет выглядеть так:
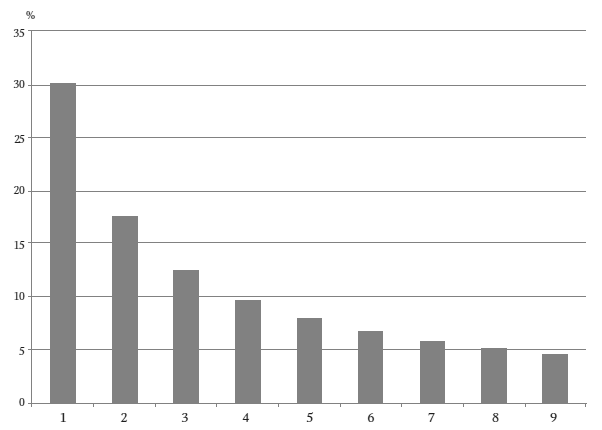
Закон Бенфорда
Гладкая кривая – это закон Бенфорда в визуальной форме.
Блестящая идея Вэриана и Нигрини состояла в том, что люди, фальсифицирующие цифры, не знают о законе Бенфорда. У растратчика или налогового мошенника нет причин думать, что какая-либо цифра должна встречаться чаще, чем другие. Поэтому массив искусственных чисел должен иметь равномерное распределение первых цифр.
Как бы то ни было, это упрощенная идея. Эксперименты по имитации случайности (о них не было широко известно) уже показали, что в сфабрикованных числах все цифры почти никогда не используются в равной мере. Альфонс Чапанис представил гистограммы полученных результатов, и распределение в них равномерным не было.
Другая проблема в том, что честные финансовые данные чаще всего в точности соответствуют кривой Бенфорда, но иногда – нет. И заранее бывает трудно сказать, с каким случаем вы имеете дело. Одним из таких примеров могут служить данные продаж магазина, где все товары стоят 99 центов. Анализ выявит большое количество девяток. Как замечает Нигрини, это указывает, что цены выдуманы, специально разработаны людьми как часть маркетинговой стратегии. Но если вы руководите таким магазином, это ваша реальность, а не мошенничество. Можно найти множество других ситуаций, когда природа бизнеса способствует распределению первых цифр, не отвечающему закону Бенфорда – по абсолютно невинным причинам.
Тем не менее, основная идея Нигрини оказалась верна: придуманные цифры отличаются от настоящих. Он стал частым гостем в здании суда Цинциннати, где разбирал преступления, в которых фигурировали цифры.
Один из первых исследованных им случаев мошенничества произошел в Аризоне. Уэйн Джеймс Нельсон, 43-летний менеджер отделения государственного казначейства в Аризоне, начал короткую карьеру растратчика с того, что выписал чек на 1927,48 доллара от штата Аризона на имя фиктивного поставщика. За следующие несколько дней он выписал еще 22 фальшивых чека на общую сумму почти 1,9 миллиона долларов.
Будучи пойманным, Нельсон утверждал: он выписывал чеки из благородных побуждений, чтобы продемонстрировать уязвимость принятой в Аризоне системы предъявления чеков к оплате. Он просто «забыл» проинформировать сотрудников казначейства об этих недостатках, а деньги направлял на собственные счета.
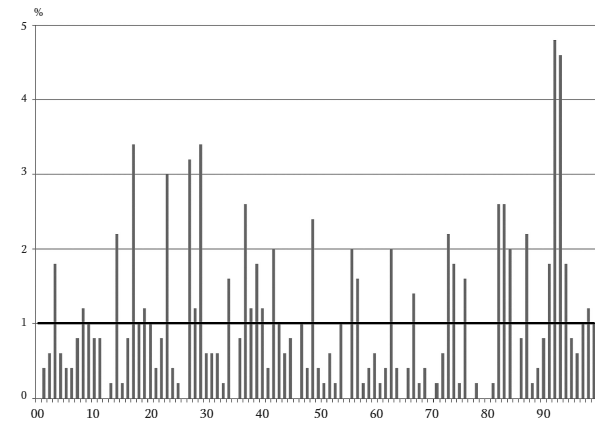
Последние две цифры: 500 придуманных чисел
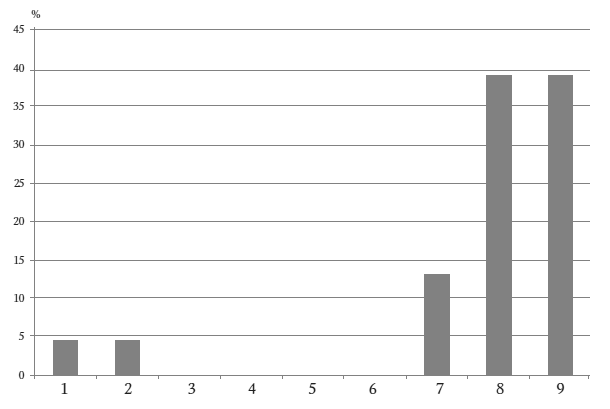
Первые цифры чеков растратчика
На первый взгляд в чеках, выписанных Нельсоном, присутствовали некоторые закономерности.
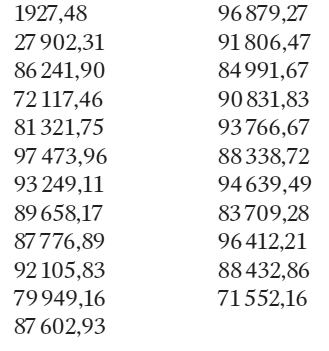
Нельсон был «анти-Бенфордом», как выразился Нигрини. Все суммы на чеках, за исключением двух, начинались с больших цифр 7, 8 и 9. Нельсон не превышал порога $100 000, вероятно, потому, что числа с шестью нулями привлекли бы нежелательное внимание.
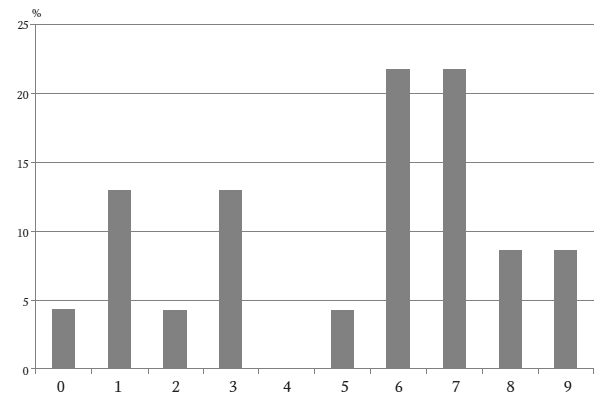
Последние цифры чеков растратчика
Ниже приведена гистограмма первых цифр в чеках Нельсона.
Фальшивые числа обычно смешиваются с настоящими. Аудитор будет анализировать не только суммы фальшивых чеков (откуда ему знать, что они фальшивые?). Он проверит все чеки Нельсона или все суммы, проходившие через его отдел. Но даже в этом случае предпочтение Нельсоном цифр 8 и 9 в фальшивых счетах выделит цифры 8 и 9 и в общем массиве данных. И это влияние можно выявить.
Нигрини обнаружил: в чеках Нельсона проявляются те же типичные особенности, что и в остальных придуманных числах. Предположим, мы пытаемся подсчитать последние (самые правые) цифры в чеках. Это единицы центов, и с финансовой точки зрения они Нельсона явно не интересовали. Тем не менее, в них наблюдается определенная закономерность. Нельсон отдавал предпочтение таким последним цифрам, как 6 и 7. Цифра 4 вообще не встречается.
Эта гистограмма очень похожа на гистограммы Чапаниса. Точно так же, как добровольцы Чапаниса, Нельсон повторялся, не отдавая себе в этом отчета. В 23 чеках он умудрился повторить 87, 88, 93 и 96 в качестве двух первых цифр. Аналогично, в качестве центов повторялись числа 16, 67 и 83.
Внутренняя налоговая служба США продает исследователям информацию из налоговых деклараций, предварительно удалив личные данные. Нигрини приобрел 100 000 налоговых деклараций за 1985 и 1988 г. и начал анализировать их на университетской мини-ЭВМ VAX. Он хотел проверить, можно ли определить, кто из налогоплательщиков жульничает.
Многие записи в налоговой декларации представляют собой сумму, разницу или производную других записей. Рассматривать их нет смысла, поскольку компьютеры налоговой службы проверяют правильность вычислений. Другие записи подтверждаются документацией третьей стороны, например, форма W-2 для заработной платы или 1099-INT для дохода от процентов. Это обеспечивает полезную возможность сравнения. Нигрини обнаружил: данные о доходе от процентов с высокой точностью соответствуют закону Бенфорда. Однако выплаченные проценты не соответствовали кривой. В то время ипотечные заимодатели не сообщали о процентах в налоговую службу. Проценты по потребительскому кредиту подлежали вычету из налогооблагаемой базы (и тоже не подтверждались документами). Это означало, что налогоплательщики испытывали искушение преувеличить выплаченные проценты, надеясь, что их не проверят. Анализ Нигрини показал, что многие именно так и поступали.
Во время президентской кампании Билл Клинтон опубликовал свои налоговые декларации начиная с 1977 г. Нигрини сумел отбраковать из налоговых деклараций Клинтона 380 сумм дохода и 511 сумм вычетов, относящихся к системе доверия. Он не обнаружил ничего подозрительного, за исключением преобладания круглых чисел – весьма распространенное явление. Так, например, старый мужской костюм, пожертвованный благотворительной организации, был оценен в 100 долларов. Совершенно очевидно, что сумма эта приблизительна – одним из признаков служит круглое число. Но указать $100 – честнее, чем придумывать точную цену вроде $107,03.
Одним из первых, кто поверил Нигрини, был Роберт Бертон, главный финансовый инспектор из прокуратуры Бруклина. В 1995 г. Бертон использовал программное обеспечение Нигрини для анализа чеков семи компаний, подозреваемых в связях с преступным миром. Бертон обнаружил свидетельства придуманных чисел и после дальнейшего расследования обвинил в мошенничестве бухгалтеров и сотрудников, выписывавших чеки. Действия инспектора удостоились хвалебной статьи в Wall Street Journal. Закон Бенфорда был назван «инструментом, достойным Шерлока Холмса». Приводились также слова Бертона: «В точку. Это мошенничество».
Статья в Wall Street Journal принесла славу закону Бенфорда, но в то же время породила миф, что он представляет собой нечто вроде волшебного детектора лжи. С тех пор метод Нигрини получил широкое распространение в правоохранительных и налоговых органах, а также в частном секторе. Сегодня повседневный анализ данных о потребителях позволяет без труда выделить для дальнейшего изучения подозрительные числа. Тем не менее, анализ цифр остается относительно новым методом, недостаточно проверенным. Очень важно понимать, чего можно, а чего нельзя добиться с его помощью.
«Я регулярно расстраиваюсь, читая о том, как люди неправильно используют закон Бенфорда», – признался мне Нигрини. Вне всякого сомнения, человек услышал о законе Бенфорда, просмотрел статью в «Википедии» и решил, что любые числа, первая цифра которых не соответствует кривой распределения, – фальшивые. Этот вывод ни в коем случае нельзя назвать верным. Существует множество причин, когда первые цифры легитимных чисел могут не подчиняться распределению Бенфорда, и поэтому проверка первой цифры редко бывает полезной. Нигрини считает, что гораздо эффективнее анализ первых двух. В результате получается гистограмма из 100 столбиков. При достаточном массиве информации (тысячи чисел) соответствующие распределению Бенфорда данные образуют на графике гладкую кривую.
Другой полезный тест анализирует две последние цифры больших чисел. Это даже не проверка «закона Бенфорда». Таким способом выявляются характерные особенности придуманных чисел, выявленные Чапанисом. Обратите внимание что тест последних двух цифр работает даже в том случае, когда данные не должны подчиняться закону Бенфорда.
В руках профессионала анализ цифр состоит из множества разных тестов, а также вычисления их статистической значимости. Первичным этапом сравнения должна быть история одного и того же набора данных. Расходы текущего квартала должны сравниваться с расходами предыдущих кварталов. Нигрини называет этот принцип «Мое правило» – по модели базовых имен, предложенных программным обеспечением для новых файлов («Мой файл», «Моя таблица» и так далее). «Мое правило» позволяет избежать самой распространенной ошибки дилетантской нумерологии, предполагающей, что все числовые базы данных в точности описываются законом Бедфорда. Это ошибочное допущение. Признаки придуманных чисел, выявленные Чапанисом, тоже не обеспечивают стопроцентной защиты. По необъяснимым причинам эти методы могут оказаться применимыми или не применимыми в каждой конкретной ситуации. Проще и надежнее использовать в качестве основы прошлые распределения цифр.
В конце концов, любое мошенничество начинается в какой-то момент времени. Если Стэн из бухгалтерии начнет жульничать в следующий вторник, это изменит распределение цифр в его суммах – независимо от того, насколько настоящие данные близки к «случайным» или соответствовали кривой Бенфорда.
В качестве иллюстрации «Моего правила» Нигрини приводит эксперимент, придуманный в 2011 г. на занятиях по математике 17-летним студентом Ка Буи из немецкого города Кобленц. Класс был поделен на пять групп по четыре студента в каждой. Одним группам выдали газеты и предложили составить список из 500 чисел, встреченных в новостях. Другим группам предложили придумать 500 чисел. Смысл эксперимента в том, чтобы проверить, можно ли отличить числа, взятые из новостей, от придуманных, только по распределению составляющих их цифр.
Чтобы максимально затруднить задачу, группам, придумывавшим числа, предложили имитировать те, что могли быть найдены в газете (в противоположность случайным). В этом случае усиливалось сходство с настоящим мошенничеством, ведь преступник похож на хамелеона.
Ни один из пяти наборов данных, настоящих и поддельных, не соответствовал кривой Бенфорда, однако с первого взгляда можно было определить, что они составляют две группы. В одной наблюдались «высокие пики» – пары двух первых цифр, встречавшиеся гораздо чаще, чем ожидалось. Во второй пики были меньше, и распределение в большей степени соответствовало кривой Бенфорда. Как мы уже убедились, повторяющиеся пары цифр могут свидетельствовать о неосознанности – или о мошенничестве. Вы можете подумать, что группа с «маленькими пиками» состояла из настоящих чисел, взятых из газет. И ошибетесь.
Вспомните, что фальшивые числа придумывали группы из четырех человек. Из-за того, что разные люди неосознанно предпочитают разные цифры, вклад каждого члена группы делился на четыре. Это затруднило выявление обмана.
Реальный признак был следующим. В газетах много раз встречалось упоминание текущего года (2011) и нескольких предшествующих. Поэтому на гистограммах отмечался пик для 20 как пары первых цифр. Составители таблицы фальшивых чисел также использовали числа, обозначающие год, но в недостаточном количестве.
Тот, кто использует закон Бенфорда и признаки Чапаниса в качестве критерия, придет к выводу, что группы данных с маленькими пиками настоящие. Однако разумнее было бы проанализировать распределение цифр в числах, взятых из других газет. Это выявило бы массовое упоминание текущего года и помогло бы правильной идентификации.
Когда цифры в числах, имеющих важное значение, не соответствуют ожидаемому распределению, хороший следователь способен выяснить причину. Тем не менее, существует пара несложных, пригодных для самостоятельного применения тестов, помогающих быстро выявить подозрительные данные. На следующих нескольких страницах я продемонстрирую некоторые способы обнаружить вероятность фальсификации или манипулирования числами. Эти тесты предназначены в основном для различения реальных данных и на 100 процентов сфальсифицированных одним человеком. Столь резкий контраст вы увидите не всегда. Тем не менее, во многих случаях именно один-единственный мошенник снабжал своих жертв полностью фальшивыми данными. Эти тесты, используемые в качестве предварительной оценки, быстры и не связаны с дальнейшим анализом, а ведь вы, скорее всего, захотите его провести.
Каждое воскресенье владелица ресторана быстрого питания начинала с того, что придумывала объем продаж в долларах за предыдущую неделю. Ей нужно было отчитываться в налоговые органы. Любая цифра была фальшивой!
Совершенно случайно бухгалтер ресторана оказался одним из студентов Нигрини. Нигрини посмотрел на придуманные числа. «Ее выдали не первые цифры», – объяснил он. Ресторан быстрого питания с устойчивым бизнесом может иметь выручку, скажем, $5000 в день, с не очень большими отклонениями. Первые цифры данных не будут соответствовать распределению Бенфорда – и не должны. Подлог выдали две последние цифры. Ни одно из чисел не оканчивалось на 00. Это весьма распространенный признак, поскольку мошенники считают, что круглые числа выглядят недостаточно случайными. Кроме того, около 6,5 процента чисел оканчивались на 40 (при ожидаемой величине всего 1 процент). Использование пары 40 для двух последних цифр – неосознанная склонность владелицы ресторана.
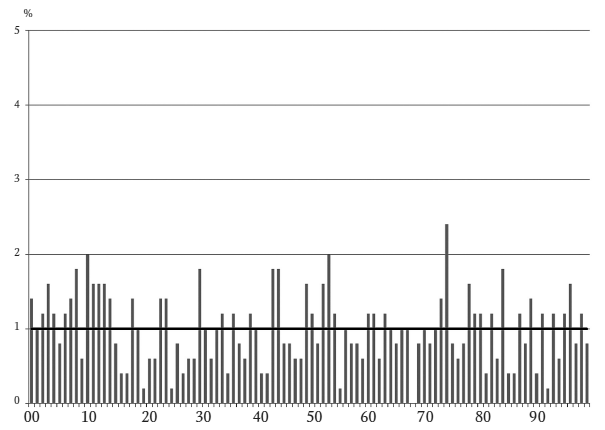
Последние две цифры: 500 случайных чисел
Когда-нибудь ресторан быстрого питания выставят на продажу, и покупатели внимательно изучат бухгалтерские документы. Возможно, для демонстрации владелица придумает новые, раздутые числа. Возникнет ли у покупателей подозрение, что вся отчетность взята с потолка?
В мелком бизнесе показатели ежедневных продаж – это сумма большого количества граф «итого» в кассовых аппаратах. Последние две цифры этих сумм обычно бывают случайными – каждая пара от 00 до 99 появляется приблизительно в 1 проценте случаев.
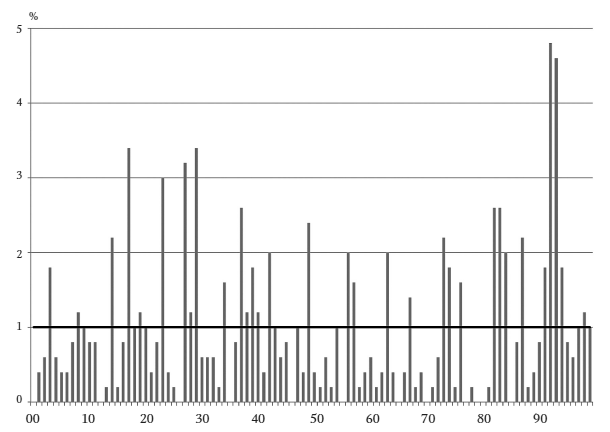
Последние две цифры: 500 придуманных чисел
Однако не во всех документах указываются суммы с точностью до цента. Иногда их округляют до долларов или даже до тысяч долларов. В таких случаях нужно использовать две крайние цифры справа.
Чтобы провести тест последних цифр, подсчитайте, сколько раз каждая из возможных пар встречается в имеющемся наборе данных. Всего таких пар 100, и поэтому потребуется составить гистограмму из 100 столбиков.
Ниже приведена гистограмма, дающая представление, как выглядят реальные данные. Она характеризует выборку из 500 случайных чисел (сгенерированных программой Excel). Число 500 достаточно репрезентативно для мелкого бизнеса – это около 17 месяцев ежедневных продаж или десять лет еженедельных. Но даже при 500 числах гистограмма получается неравномерной, с довольно большими вариациями. В данном случае одна пара цифр (68) не появляется совсем, а три пары (10, 53 и 74) встречаются в два раза чаще, чем ожидаемый 1 процент. Это нормальные отклонения, характерные для случайных данных.
Теперь посмотрим на сфабрикованные данные.
Следующая гистограмма отображает распределение двух последних цифр в 500 числах, придуманных человеком. Более сильные вариации видны даже с первого взгляда. Две пары (93 и 94) встречаются более чем в 4 процентах чисел, что маловероятно для реальных данных. Двенадцать пар не встречаются вообще, и это тоже крайне маловероятно.
Задайте себе следующие три вопроса. Утвердительный ответ на любой из них должен усилить ваши подозрения.
a) По непонятной причине есть пара (или пары) цифр, встречающиеся чаще остальных?
б) Частота повторения сдвоенных цифр (особенно 00 и 55) меньше средней?
в) Убывающие пары (10, 21, 32, 43, 54, 65, 76, 87, 98) явно встречаются чаще других?
В приведенном примере ответ на вопрос (a) утвердителен. Кроме того, в массиве данных нет сдвоенных цифр (б). Приблизительно 10 процентов всех чисел должны оканчиваться на сдвоенные цифры. У нас таких 20 из 500, всего 4 процента. Пары 00, 55 и 77 вообще не встречаются.
Из 500 пар последних цифр 44 – убывающие. Это почти точно ожидаемые 9 процентов (из 100 возможных пар девять убывающие). Так, по критерию (в) данные не вызывают подозрений.
Наш набор данных не прошел два из трех тестов. Будь это суммы продаж мелкого бизнеса, стоило бы запросить дополнительную или более подробную информацию – и посмотреть, как отреагирует продавец.
Нет нужды беспокоиться, что вам придется считать вручную. На практике все это делается с помощью функций «копировать» и «вставить». Попросите данные в виде таблицы Excel или в совместимом с ней формате, чтобы без труда перенести их в шаблон теста, использующего закон Бенфорда. Примеры таких тестов можно бесплатно найти в интернете, в том числе один тест Нигрини (NigriniCycle.xlsx). Перенеся данные, выполните инструкции и заполните определенные столбцы заранее известными формулами. Результатом будут отформатированные гистограммы для двух последних цифр и итоги других распространенных тестов. Кроме того, программа вычисляет математическую оценку статистической значимости, что, конечно, гораздо надежнее простого просмотра полученных данных.
Резюме: Как распознать фальшивые числа
• Когда распределение цифр в последней группе данных отличается от обычного распределения, характерного для данной компании, это может быть признаком подлога.
• Растратчики и мошенники, придумывающие числа, неосознанно отдают предпочтение убывающим парам цифр (таким как 10, 21, 32 и так далее).
• Мошенники реже пользуются сдвоенными цифрами (например, 00 или 55), полагая, что они выглядят недостаточно «случайными».
Назад: 10 Как интерпретировать рейтинги, полученные с помощью краудсорсинга
Дальше: 12 Как распознать числа, которыми манипулировали

