ЧТО ТАКОЕ ВЕРОЯТНОСТЬ

Вероятность наступления какого-либо события измеряется в простых дробях или процентах. Если что-то произойдет наверняка (например, насколько вероятно, что в следующем году пойдет дождь?), вероятность равна 1, или 100%. Если что-то определенно не должно случиться (например, насколько вероятно, что у вас вырастут крылья?), вероятность равна 0, или 0%. Если же событие в равной степени либо произойдет, либо нет (например, каковы шансы, что вы подбросите монетку и выпадет «орел»?), вероятность равна 1/2, или 50%.

Когда событие крайне маловероятно, то проще сказать нечто вроде «вероятность выиграть джекпот в национальной лотерее Британии — примерно один шанс из 14 миллионов». Или, если точнее, это один шанс из 13 983 816, что соответствует дроби 1/13983816. Переводим ее в проценты и получаем 0,00000715%.

Игральные кости

У обычной игральной кости шесть граней, поэтому шанс выбросить какое-либо конкретное число равен 1/6, или 16,7%. Если же кидать две кости, может выпасть любая из 36 различных комбинаций.

Предположим, вам нужно выбросить 12 очков. Для этого должны выпасть две шестерки, и такой вариант только один среди 36 возможных комбинаций. Поэтому вероятность этого события составляет 1/36 = около 2,8%.

Теперь допустим, что вы хотите получить сумму костей, равную 3. Для этого должно выпасть 2 и 1 либо 1 и 2, то есть всего две подходящие комбинации. Ваши шансы: 2/36 = 1/18 = около 5,6%.

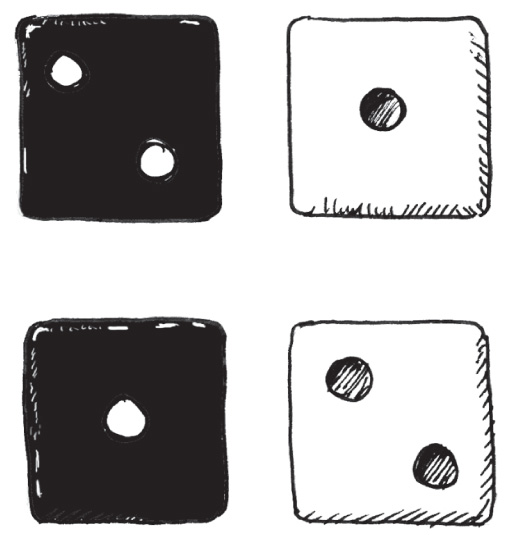
Чаще всего на костях выпадает сумма 7, поскольку для этого подходят шесть различных комбинаций. Вероятность такого события равна 6/36 = 1/6 = 16,7%.

Дни рождения

А теперь, пожалуй, самое странное утверждение в этой книге: если в результате случайного отбора собрать в одной комнате 30 человек, вероятность того, что двое из них родились в один день, составит 70%!

Чтобы это доказать, сперва выясним, каковы шансы, что ни у кого из 30 собравшихся дни рождения не совпадают (будем считать за совпадение одинаковый день и месяц, без учета года). Сначала в комнате находится один Фред, затем входит Джанет. Какова вероятность, что она родилась не в один день с Фредом? Будем считать, что в году 365 дней, и игнорировать високосные годы, потому что на ответ это практически не повлияет, но существенно усложнит вычисления.

Вероятность того, что Джанет родилась в один день с Фредом, равна 1/365. Следовательно, вероятность, что она не родилась с ним в один день, составит 364/365.

Третьим появляется Барни, и если день рождения Джанет не совпадает с днем рождения Фреда, то вероятность, что Барни не родился в один день с кем-то из них, равна 363/365. А вероятность того, что все трое родились в разные дни, составит:

364/365 × 363/365 = 99,18%

Входит Агнесс. Вероятность, что ее день рождения не совпадает с другими, равна 362/365, а вероятность, что все четверо родились в разные дни, составит:

364/365 × 363/365 × 362/365 = 98,37%

Постепенно комната заполняется, и мы перемножаем все больше и больше дробей, вычисляя вероятность несовпадения дат дней рождений. Когда в комнату заходит двадцать третий человек, происходит нечто странное. И наше уравнение приобретает следующий вид:

364/365 × 363/365 × 362/36 x… и так далее… × 345/365 × 344/365 × 343/365 = 49,27%

То есть шансов, что все родились в разные дни, теперь меньше 50%, а значит, вероятность совпадения дней рождения у двух человек уже немного превышает 50%. Выходит, такое совпадение скорее имеет место быть, чем не имеет!

К тому моменту, как в комнате соберется 30 человек, вероятность, что дни рождения у всех разные, снизится примерно до 30%, а вероятность, что двое из присутствующих родились в один день, составит около 70%. Если вам сложно в это поверить, в следующий раз, когда рядом окажутся 30 человек, поинтересуйтесь, когда они родились. Да, это удивительно, но факт.

Карты и покерные комбинации

Предположим, у вас есть обычная колода из 52 игральных карт и вы хотите знать, какова вероятность выпадения той или иной карточной комбинации. Некоторые из этих вероятностей довольно легко просчитать.

Каковы шансы, что вверху колоды будут две совпадающие по номиналу карты

Если перетасовать колоду и снять верхнюю карту, она может оказаться любой, например четверкой треф. В колоде есть еще три совпадающие с ней по номиналу карты: четверка червей, четверка пик и четверка бубей. Всего остается 51 карта, следовательно, вероятность, что следующая карта совпадает с уже открытой, составит 3/51. Эту дробь можно сократить, разделив числитель и знаменатель на 3, получаем 1/17.

Иначе говоря, если многократно перетасовывать колоду и открывать две верхние карты, две совпадающие карты в среднем будут выпадать один раз из 17.

Каковы шансы, что вам сдадут пять карт одной масти

Если вы играете в покер, это, к вашей великой радости, будет флеш. Но насколько это вероятно?

Первое, что нужно понимать: не имеет значения, берете ли вы пять карт сверху перетассованной колоды или сидите за одним столом с другими игроками и получаете карты по одной во время раздачи. Так что представим, что вы просто взяли из колоды пять верхних карт.

Верхняя карта может быть любой. Очевидно, что по масти она совпадает с собой же, то есть вероятность совпадения равна 1 (или 100%). Положим, это семерка бубей. Из оставшейся 51 карты 12 имеют ту же масть, стало быть, шанс, что и следующая карта совпадет по масти, составит 12/51.

Для третьей карты вероятность совпадения равна 11/50, поскольку среди 50 оставшихся карт 11 нужной масти, для четвертой карты — 10/49, а для пятой — 9/48. Чтобы вычислить вероятность совпадения масти для всех пяти карт, перемножим все эти вероятности.

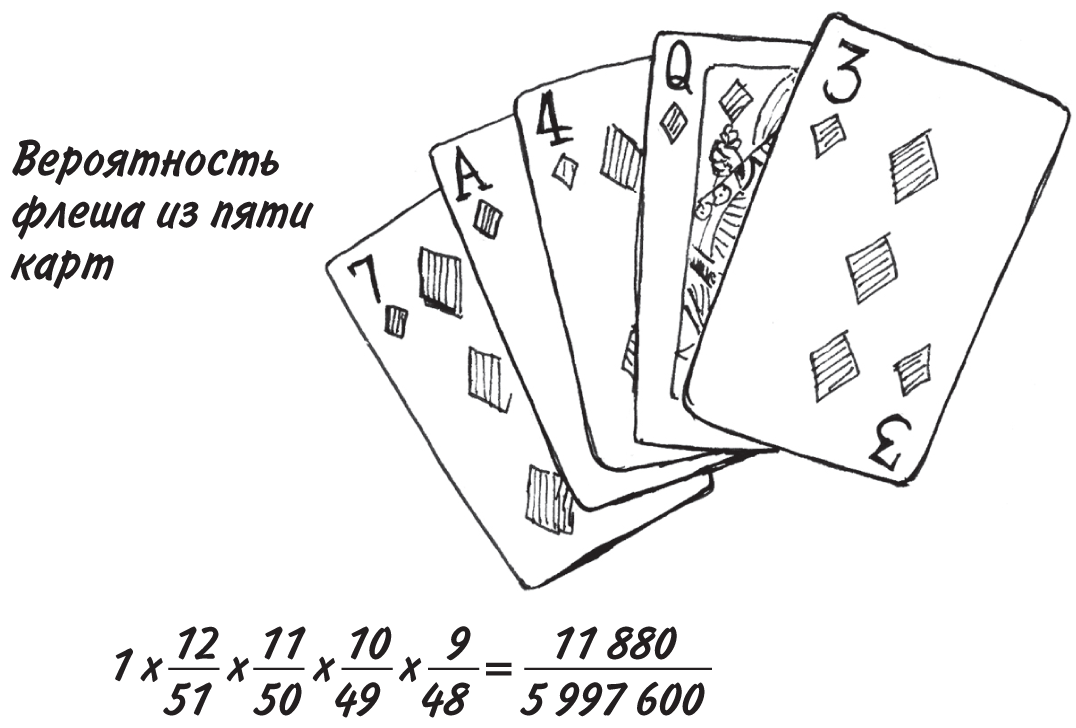
Округлим последнюю некрасивую дробь: число 11 880 близко к 12 000, а 5 997 600 к 6 000 000. Это даст нам

12 000/6 000 000 = 1/500

Таким образом, ваш шанс получить подряд 5 карт одной масти примерно равен 1 из 500, или 0,2%.

Покерный трюк на 10 карт

Как видите, любой фулл-хауз бьет тройку, а тройка бьет две пары. Вот трюк, которому я научился в Дублине у своего коллеги Роба Истэвея, тоже автора книг по математике. Предупреждаю: мы не несем никакой ответственности за то, как вы будете использовать эти сведения.

Вам понадобятся десять карт из колоды: три тройки и любая одиночная карта.

Играть нужно с другом — вы раздаете по пять карт ему и себе. Коварство фокуса в том, что вы с самого начала знаете, кто победит, а кто проиграет!

Секрет исключительно прост. Независимо от того, как перетасованы карты, игрок, которому достанется одиночная карта, проиграет! Если вы привыкли обращаться с картами, вам не составит труда придержать одну карту вверху или внизу колоды и убедиться, что она досталась нужному игроку. Если же вы не уверены в себе, слегка согните уголок одиночной карты, чтобы видеть, кому она досталась, и знать, кто победит.

Имеет смысл позволить вашему другу несколько раз вы­играть, а затем, когда он утратит бдительность, поднять ставки и отыграться.

Некоторые забавные вероятности

Люди обожают судачить о всяких странных случайностях. Вот их небольшая подборка, но не принимайте ее слишком всерьез!

• Шансы найти четырехлистный клевер: 1 из 10 000, или 0,01%.
• Вероятность, что беременная женщина вынашивает более чем одного ребенка, постепенно возрастает. На сегодняшний день шанс зачать двойню, тройню, а то и больше составляет примерно 3%.
• Если во время того, как вы целитесь в мишень, играя в дартс, кто-то вдруг завяжет вам глаза и несколько раз повернет на месте, вероятность, что вы попадете в мишень вслепую, равна примерно 2%. При этом шанс попасть в яблочко составит 1 из 100 000. Но, пожалуйста, не стоит проверять это на практике.
• Вероятность при игре в гольф забить мяч с одного удара составляет предположительно 1 из 5000.
• Вероятность, что вас поразит молния, примерно 1 из 3 000 000. По любопытному совпадению, такова же вероятность повстречать инопланетянина.
• Вероятность, что в следующем столетии в нашу Землю врежется астероид, составляет 1 из 5000. И если этот огромный гадкий астероид таки сделает свое грязное дело, каковы шансы, что аккурат перед этим вы повесите сушиться белье? Примерно 100%.
• Какова вероятность получить высший балл на экзаме­национном тесте, отмечая варианты наобум? Если в тес­те 30 вопросов, каждый с четырьмя вариантами ответа, то вероятность составит 1 из 4³⁰ = 1 152 921 504 606 846 976. Если же для прохождения теста достаточно угадать не менее 50% ответов, шансы на победу вычислить гораздо сложнее, но это будет примерно 1 шанс из 364. Впрочем, есть и хорошие новости: вероятность ответить неправильно на все вопросы составляет лишь 1 из 5600.

Две обманчивые вероятности

Люди часто заблуждаются, оценивая свои шансы на удачу, а вокруг, увы, полно бессовестных типов, которые этим пользуются, вовлекая доверчивых искателей легкого счастья во всевозможные аферы, а затем облапошивая их. Если вы один из таких прощелыг, вот пара несложных трюков вам на радость. Суть их в том, чтобы сначала убедить жертву, что удача на ее стороне, а затем обчистить до нитки.

Черные и белые карточки

И вот вы сидите за столом с бедным стариной Малькольмом и показываете ему три карточки: одна черная с обеих сторон, другая — белая, а третья с одной стороны черная, а с другой — белая.

Попросите Малькольма перетасовать не глядя карточки под столом, затем вытащить одну карточку и положить ее на стол так, чтобы никто из вас не заметил цвета нижней стороны. Остальные две карточки никто не должен видеть. Пусть верхняя сторона лежащей на столе карточки будет черная.

— Очевидно, это не белая с двух сторон карточка, — говорите вы, — значит, она или черная с белым, или черная с обеих сторон.

Малькольм глубокомысленно кивает в ответ.

— Выходит, что с равными шансами это та или другая карточка. (Малькольм снова кивает.) Спорим на один фунт, что другая сторона черная!

— Нет, спасибо, — отвечает Малькольм. Он что-то подозревает, хотя и не понимает, в чем подвох.

— Ой, да ладно, — подначиваете вы. — Знаешь, давай так: если другая сторона черная, ты платишь мне один фунт, а если белая, я плачу тебе полтора фунта. Годится?

Малькольму это предложение кажется слишком заманчивым, он кладет деньги на стол… и с вероятностью 2 шанса из 3 вы выигрываете. Иными словами, в среднем за три кона игры вы заплатите Малькольму полтора фунта, а он вам два.

А секрет вот в чем: какого бы цвета ни была верхняя сторона карточки, всегда ставьте на то, что другая сторона того же цвета. У двух карточек цвета сторон совпадают, и лишь у одной — разные. Поэтому у Малькольма всего один шанс на вы­игрыш из трех.

Если Малькольм всерьез задумается, он может догадаться, в чем дело, так что пора переходить ко второму трюку.

Трюк с двумя монетами

Этот трюк очень прост, но при этом весьма необычен! Идеально будет провернуть его с Малькольмом, когда он придет вместе со своей подругой Сандрой. Сандра поможет вам облегчить карманы Малькольма; нужно лишь, чтобы она выполняла ваши просьбы и не подсказывала Малькольму.

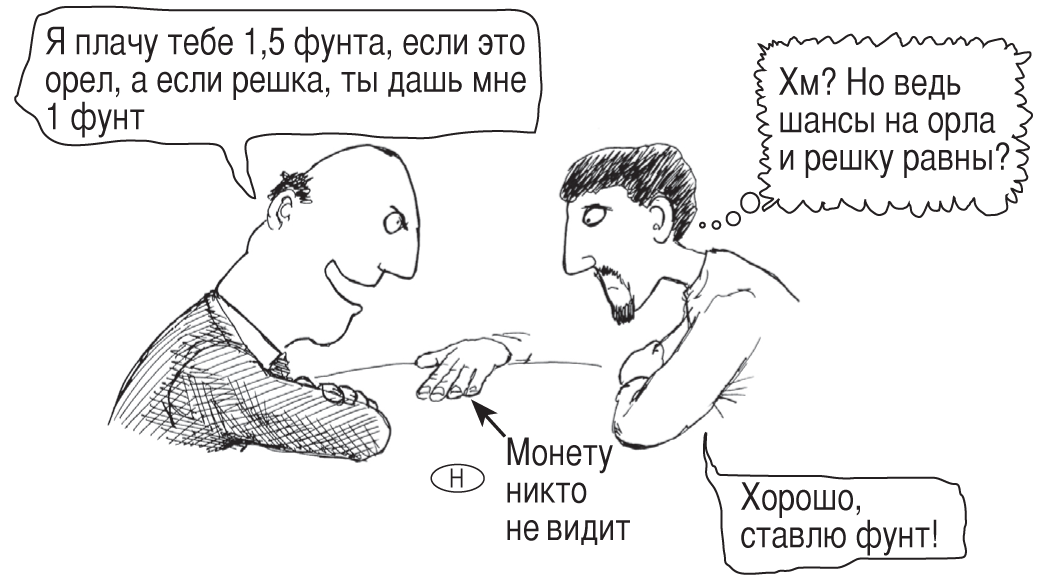
И что же получается, сделка выгодна для Малькольма? Конечно, нет. На самом деле вы снова должны выиграть с вероятностью 2 из 3. Хитрость в том, что при бросании монет кажется, будто есть три варианта того, как они могут лечь: два орла, две решки или орел и решка. Однако, взяв монеты разных размеров, вы увидите, что вариантов четыре:

Вы просили Сандру заново бросить монеты, если выпадут две решки, так что этот вариант исключен. Значит, когда дело дойдет до ставок, останется только три варианта. Когда Сандра покажет орла, в двух вариантах вторая монета лежит решкой. Поэтому в двух случаях из трех вы должны выиграть.

Прибыль букмекера

Предположим, перед вами стоит мешок с 12 шариками: один черный, 8 белых и 3 серых. Ваша задача — с закрытыми глазами вынуть один шарик из мешка. Если он черный, вы выиграли, но каковы шансы на победу? Очевидно, 1 из 12, что можно записать как 1/12.

Или же можно сказать, что есть 11 вариантов не вынуть черный шарик против одного варианта выигрыша. Получается коэффициент против выигрыша 11 к 1, который букмекеры обычно записывают как 11/1. Так они и рассчитывают ставки.

Букмекер, который не планирует получить прибыль, предложит вам коэффициент 11/1 против того, что вам попадется черный шарик. Если вы поставите 1 фунт и проиграете, фунт останется у букмекера. Если вы поставите 1 фунт и выиграете, он вернет ваш 1 фунт плюс еще 11 фунтов выигрыша.

Предположим, вы вынимаете шарики из мешка по одному. Вам известно, что 11 раз вы проиграете, а 1 раз выиграете. Если букмекер каждый раз будет предлагать вам коэффициент 11/1 после того, как вы достанете последний шарик, вы заплатите ему 11 × 1 фунт = 11 фунтов. Он же заплатит вам 1 × 11 фунтов = 11 фунтов, так что это честный, или чистый, коэффициент.

Вы решаете, что шансы вытащить черный шарик слишком малы, и потому хотите попытаться достать один из 8 белых шариков. Тогда вероятность вашего выигрыша составит 8/12. Букмекер говорит, что шансы против вашего выигрыша 4 к 8, то есть чистый коэффициент равен 4/8, или, после сокращения, 1/2. Если вы поставите 1 фунт и вытащите белый шарик, вы выиграете 1/2 × 1 фунт = 50 пенсов.

Как переводить букмекерские коэффициенты в вероятности

Наш букмекер также предлагает коэффициент 3 к 1 против того, что вы достанете один из серых шариков. Чтобы убедиться, что это чистый коэффициент, нужно преобразовать его в вероятность выбора серого шарика и посмотреть, верна ли она.

Из букмекерского коэффициента следует вероятность 1/4. Поскольку в мешке 3 серых шарика из 12, это дает вероятность 3/12, то есть 1/4. Выходит, это чистый (честный) коэффициент!

А вот хитрый момент. Положим, нам неизвестно, сколько в мешке шариков, мы только знаем, что они белые, серые и черные. Можно определить, насколько букмекер честен, посмотрев на все его коэффициенты, преобразовав их в вероятности и сложив их.

Черный шарик: коэффициент = 11/1, вероятность = 1/12

Белый шарик: коэффициент = 1/2, вероятность = 2/3

Серый шарик: коэффициент = 3/1, вероятность = 1/4

Если букмекер абсолютно честен, сумма вероятностей даст 1. Можно сложить три простые дроби или взять калькулятор, перевести их в десятичные и уже затем складывать, но в любом случае сумма вероятностей равна 1. Какой благородный букмекер! Жаль, что в реальности таких не существует.

Ставки в спорте (и вероятность того, что Элвис работает в кафетерии)

Что касается ставок в спорте, то здесь не получится столь же легко найти вероятности, как для шариков в мешке. Более того, букмекер не может быть честным в том смысле, о котором мы говорили выше, ведь ему нужно получать прибыль, чтобы платить за свою спортивную машину, массивный золотой браслет и виллу в Португалии.

Давайте полюбуемся на Честного Сида и выясним, какую прибыль он надеется получить.

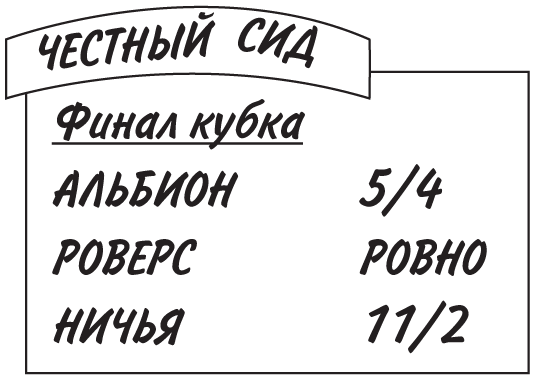
Сперва преобразуем коэффициенты Сида в вероятности: для 5/4 вероятность будет 4/9 или 0,444, «ровно» означает 1/1, то есть вероятность 1/2, или 0,5, а для 11/2 вероятность составит 2/13, или 0,154. Если сложить все десятичные дроби, получится 1,098.

Это говорит о том, что на каждые 100 фунтов, выплачиваемые Сидом, по его ожиданиям должно прийтись 100 фунтов × 1,098 = 109,80 фунта, то есть его прибыль должна составить 9,80 фунта.

Некоторые букмекеры также принимают ирреальные ставки: к примеру, на то, что Элвиса Пресли найдут живым-здоровым и что он работает в кафетерии. Уж лучше купить лотерейный билет, и хотя шанс сорвать джекпот составляет лишь 1/13983816, по сути, это куда более вероятно. Как сказал бы сам Король рок-н-ролла: «Ну что же, раз (из примерно 14 миллионов) это ради денег...».

Отправить