ДЛИНА, ПЛОЩАДЬ И ОБЪЕМ
Если вы испекли торт, перевязали его ленточкой и завернули в кулинарную пленку, то вы имели дело с длиной (ленточки), площадью (размером куска кулинарной пленки) и объемом (торта). Предположим, вы разделили содержимое большой миски с тестом на три равные части, а затем испекли из них три пирожных разной формы.
Несмотря на то что объем всех трех частей одинаков, количество пленки и длина ленточки для каждого пирожного могут отличаться. Так происходит потому, что длина, площадь и объем описывают разные свойства предметов. И в этом нужно разбираться независимо от того, занимаетесь вы готовкой или планируете ремонт в доме.
Длина
Длина — это расстояние между двумя точками. Каким бы оно ни было, с ним связано только одно измерение. Длина карандаша может равняться 130 мм, длина беговой дорожки — 100 м, а расстояние от Килмарнока до Нориджа — 705 км (или 438 миль). Миллиметры (мм), метры (м) и километры (км) — это единицы измерения длины.
Предположим, вам нужно установить новую телевизионную розетку, а для этого понадобится купить кусок кабеля. Вы идете в магазин, вооружившись планом своей гостиной.
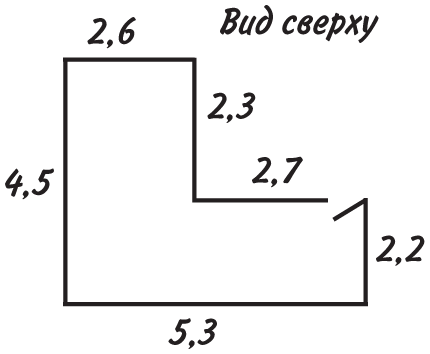
Кабель требуется протянуть от старой розетки до новой. Вы знаете длину всех стен, кроме тех, что помечены буквами a и b. Какой длины нужен провод?
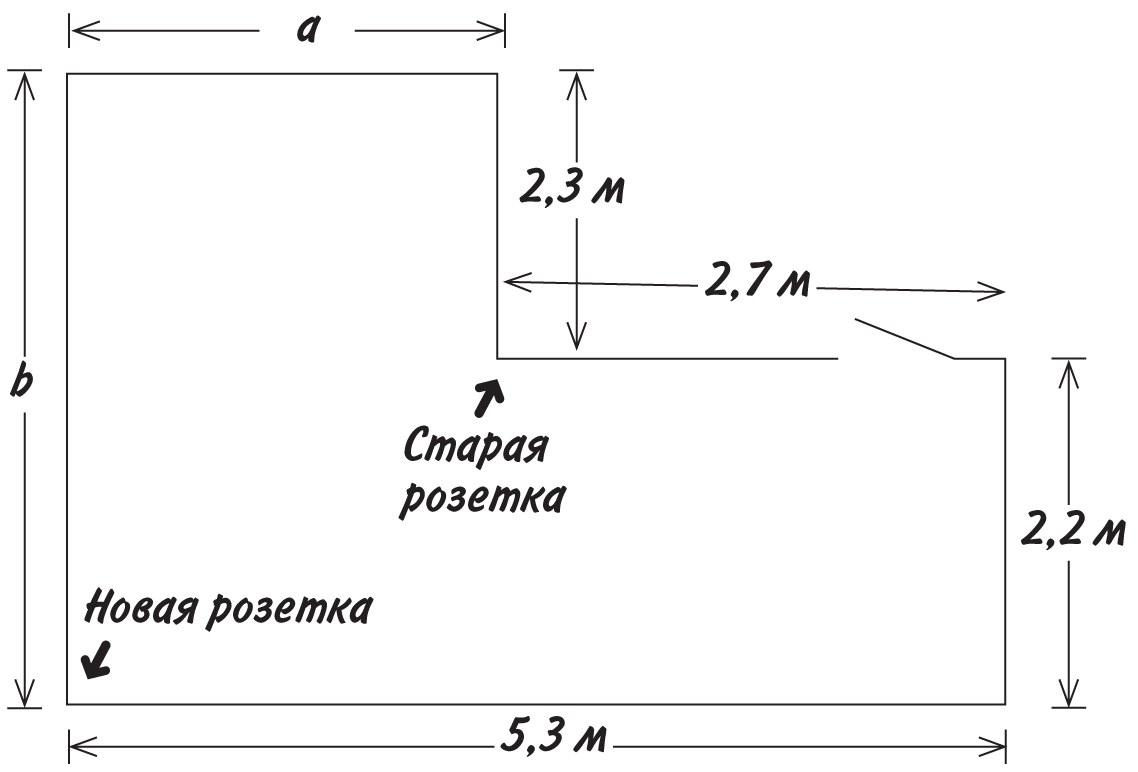
Самый простой подход — не связываться с лишними расчетами и проложить провод рядом с дверью. В этом случае его длина составит 2,7 + 2,2 + 5,3 = 10,2 м плюс еще немного понадобится, чтобы обвести кабель вокруг двери. Однако более разумный способ — вычислить a и b. Из плана комнаты следует, что длина большой стены равна 5,3 м, а той, что поменьше, — 2,7 м. Значит, длина стены а равна 5,3 − 2,7 = 2,6 м. Аналогично b = 2,2 + 2,3 = 4,5 м. Если не связываться с дверью и тянуть кабель в другую сторону, его длина должна составить 2,3 + a + b. Подставив значения a и b, получим 2,3 + 2,6 + 4,5 = 9,4 м.
Искривление пространства
Прямая линия представляет собой кратчайшее расстояние между двумя точками… если только мы не имеем дело с искривленным пространством! Обычно мы считаем, что прямая линия проведена на двумерной поверхности, например на листе бумаги. Можно взять карту мира и провести прямую линию, обозначив кратчайшее расстояние между Северным и Южным полюсом, но действительно ли оно будет кратчайшим?
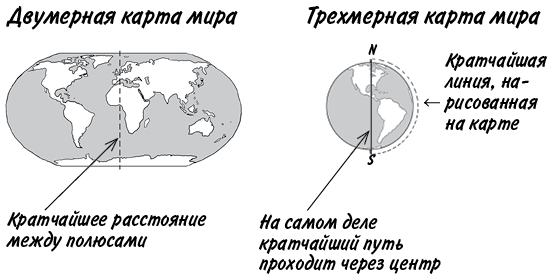
Реальный мир, в котором мы живем, представляет собой трехмерное пространство. В нем наша прямая линия становится кривой, а действительно кратчайший путь от полюса к полюсу проходит через центр Земли. (Его длину мы рассчитаем чуть позже.) Вот бы выйти в четырехмерное пространство — возможно, там найдется еще более короткий путь! О похожих вещах думал Эйнштейн, когда разрабатывал теорию относительности.
Площадь
Что ж, с длиной мы разобрались, теперь выясним, сколько понадобится краски на покраску стены b, длина которой, как мы уже знаем, равна 4,5 м.
Итак, вы покупаете в строительном магазине 750-миллилитровую банку замечательной краски цвета подгоревшей яичницы. На этикетке указано, что одного литра хватает на 12 м2 поверхности.
Первое, на что стоит обратить внимание, это обозначение м², то есть квадратные метры — единица измерения площади. Вы можете красить поверхность любой формы, но, как бы то ни было, 1 литра краски хватит на площадь 12 квадратов 1 м × 1 м. Так сколько же вы покрасите содержимым одной банки? 750 миллилитров — это 0,75 литра, следовательно, одной банки достаточно для покраски 12 × 0,75 = 9 м2.
Вычисляем площадь стены
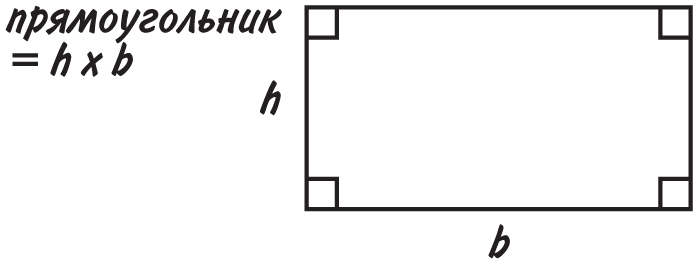
Я думаю, вы уже поняли, что знать длину стены недостаточно, поскольку расход краски также зависит от ее высоты. Существует множество формул для вычисления площадей разных фигур, и все они тем или иным образом связаны с перемножением двух длин. Сейчас мы имеем дело с самой распространенной фигурой — прямоугольником, и формула в этом случае исключительно проста:
площадь прямоугольника = ширина × высота
Предположим, что высота стены комнаты 2,5 м, а длина 4,5 м. Чтобы узнать площадь, нужно перемножить высоту и длину: 2,5 м × 4,5 м = 11,25 м2.
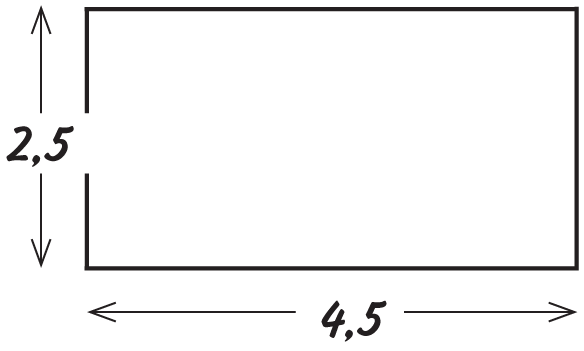
Как видите, при умножении метров на метры получаются квадратные метры.
Итак, теперь мы знаем, что площадь стены равна 11,25 м2, а банки хватает на 9 м2. Без всяких подсчетов становится очевидно, что одной банкой мы не обойдемся. Однако если мы купим две банки, останется много лишней краски, да и красить только одну стену как-то неправильно. Так что давайте поднатужимся и выясним, сколько краски понадобится для покраски всех стен в комнате. Есть два способа это сделать. Первый — вычислить площадь каждой стены и затем сложить результаты. Поскольку высота всех стен 2,5 м, получается вот что: (4,5 × 2,5) + (5,3 × 2,5) + (2,2 × 2,5) + (2,7 × 2,5) + (2,3 × 2,5) + (2,6 × 2,5)… Тьфу!
Гораздо проще вообразить, что все стены расположены в ряд.
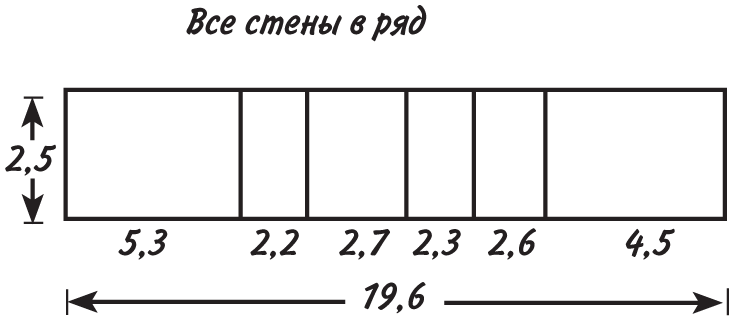
Сложив длины всех стен, мы узнаем, что их общая длина равна 19,6 м, а умножив это число на 2,5, вычислим общую площадь стен: 19,6 × 2,5 = 49 м2.
Банки краски хватает на 9 м2, стало быть, нам нужно: 49 ÷ 9 = 5,44, то есть шести банок будет вполне достаточно.
Если хотите рассчитать площадь для покраски более точно, можно измерить дверной проем и окна и вычесть их. Размер двери обычно равен 0,75 м × 2 м = 1,5 м2. Теперь подумайте об окнах: они такие же, как дверь? В половину двери? Или еще меньше? Впрочем, если вам неохота возиться с окнами, просто закрасьте их — сэкономите на занавесках.
Кирпичи и блоки
Если вы решили возвести стену из стандартного строительного кирпича, вам понадобится около 60 кирпичей на 1 м2. Если же использовать строительные блоки, то 10 блоков на 1 м2.
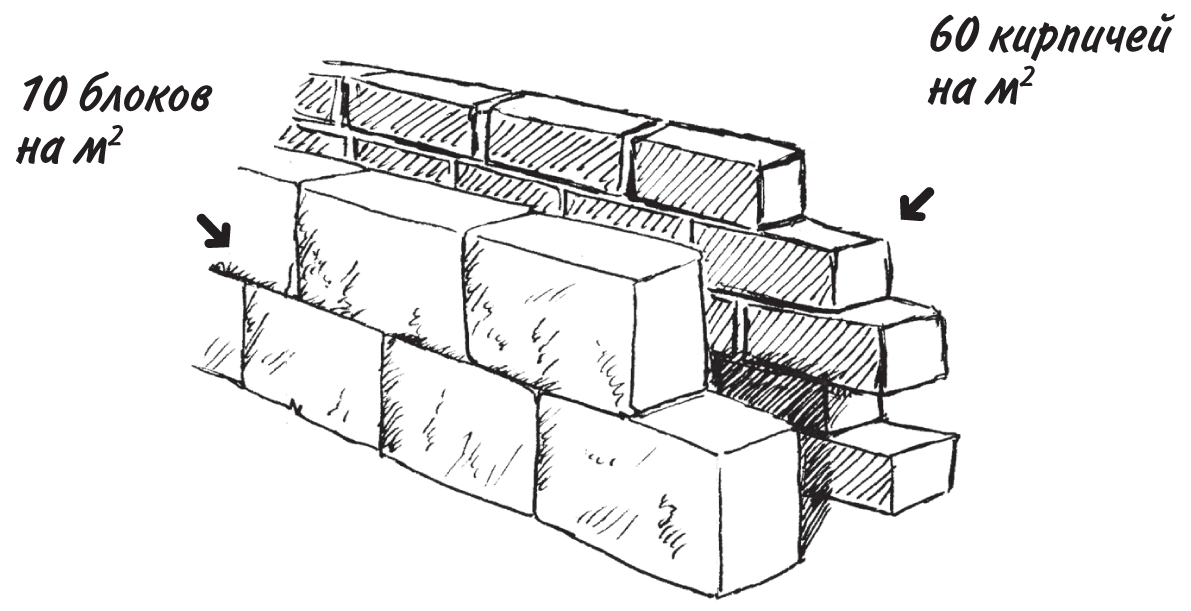
Так что если заблудший дорожный каток мимоходом развалит стену вашего дома, размер которой 5,3 м × 2,5 м, то на восстановление ее внешней части понадобится 5,3 × 2,5 × 60 = около 800 кирпичей, а внутренней — 5,3 × 2,5 × 10 = примерно 135 блоков. Если бы мой приятель Блейки знал об этом, ему бы не пришлось краснеть, когда каменщику, которого он нанял на день, уже к 11 утра не хватило материалов.
Покраска потолка
Краска цвета подгоревшей яичницы настолько вам приглянулась, что вы решили покрасить ею и потолок тоже. Так что нам опять нужно вычислять площадь. Увы, это не идеальный прямоугольник, но мы можем разделить потолок на два прямоугольника, по отдельности подсчитать их площадь и сложить результаты. Сделать это можно двумя способами.
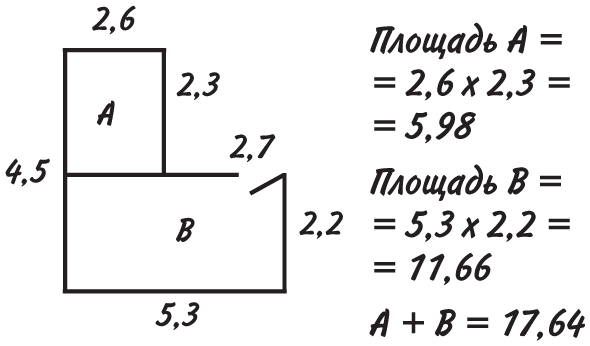
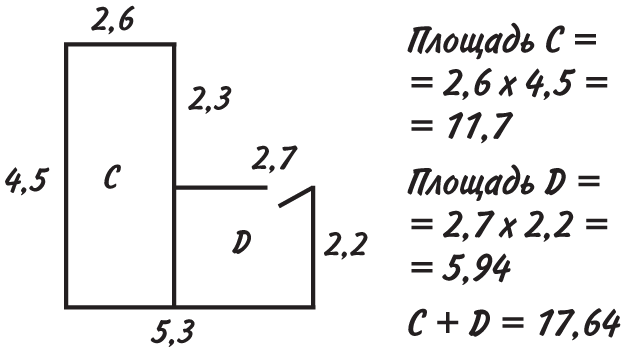
Теперь мы знаем, что площадь потолка равна 17,64 м2. Поскольку банки краски хватает на 9 м2, для потолка двух банок будет достаточно.
Формулы площадей для других фигур
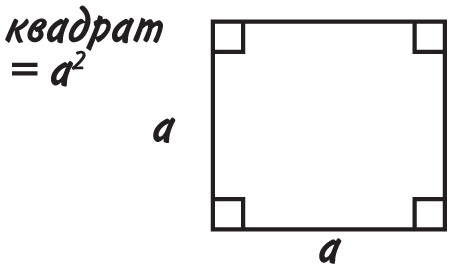
Мы уже использовали формулу площади прямоугольника. Квадрат — это тоже прямоугольник, только с одинаковыми сторонами, поэтому, чтобы вычислить его площадь, нужно умножить длину стороны саму на себя.
Прямоугольный треугольник — это прямоугольник, разрезанный пополам по диагонали. Поэтому все просто, его площадь = 1/2 × (две короткие стороны треугольника [катеты], помноженные друг на друга).
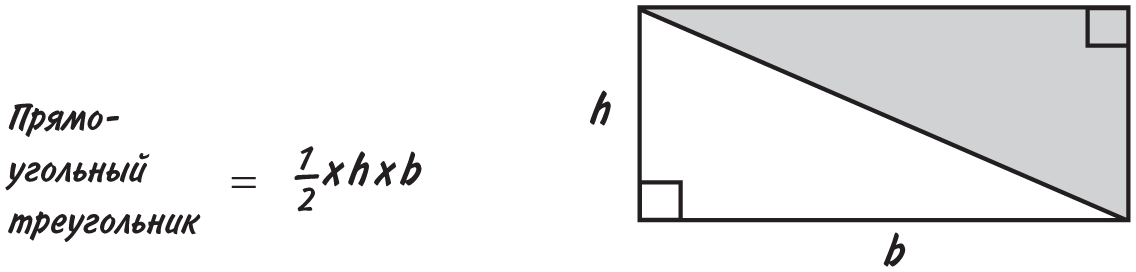
В сущности, площадь любого треугольника равна половине площади наименьшего прямоугольника, в который его можно вписать. На рисунке видно, что две серые области равны двум половинам треугольника. Формула записывается так: площадь = 1/2 × основание × перпендикулярная высота.
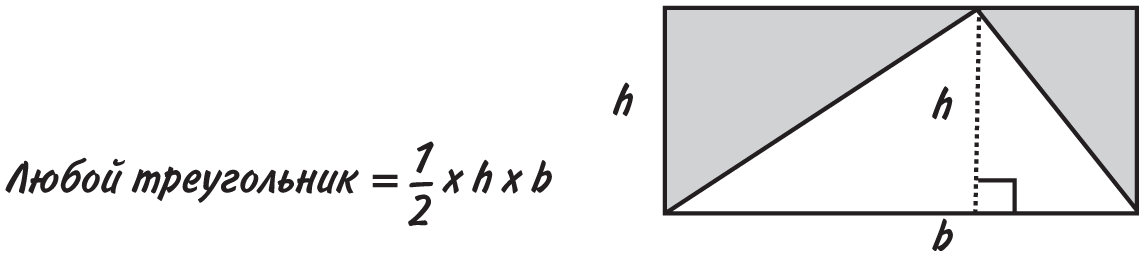
Несмотря на то что этим формулам для треугольников уделяется много внимания на уроках геометрии, вам вряд ли доведется применять их в жизни. А вот еще две более бесполезные формулы (разве что стены и потолки в вашем доме уж очень экзотической формы).
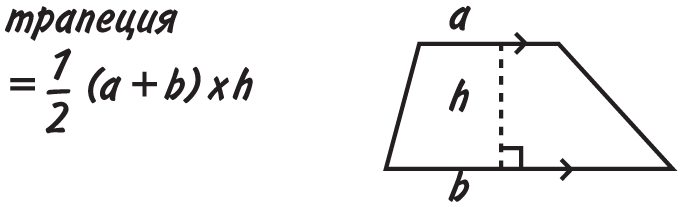
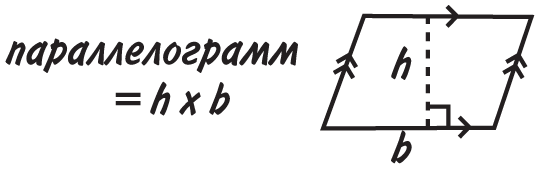
Маленькими стрелочками отмечены параллельные линии. Для использования этих формул обязательно нужно знать перпендикулярную основанию высоту h.
И наконец, вот как вычислить размер некоей области на карте. Если сторона каждой клетки соответствует 0,1 км, то площадь клетки равна (0,1)2 = 0,01 км2. Допустим, озеро занимает около 35 клеток, тогда его площадь составит примерно 0,35 км2.

Объем кубоида
Длина требует одного измерения, площадь — двух перемноженных измерений, а объем — трех. Проще всего вычислять объемы кубоидов, то есть ящиков с прямоугольными стенками. Достаточно перемножить длину, ширину и высоту — и объем получен!
Если вы решите превратить одну из своих спален в огромный аквариум для своего домашнего питомца осьминога, вам будет интересно знать вес того количества воды, которым ее можно заполнить доверху. Сначала нужно рассчитать объем комнаты: при размерах 4 м × 3 м × 2,5 м он будет равен 4 × 3 × 2,5 = 30 м3. Как видите, объем измеряется в м³, или кубических метрах. Объем 30 м3 соответствует количеству воды, которое поместится в 30 кубах с размером стороны 1 м. Как мы знаем из подраздела «Метры, литры и граммы», один кубический метр воды весит 1 тонну, значит, ваша наполненная водой спальня будет весить 30 тонн. Что ж, удачи!
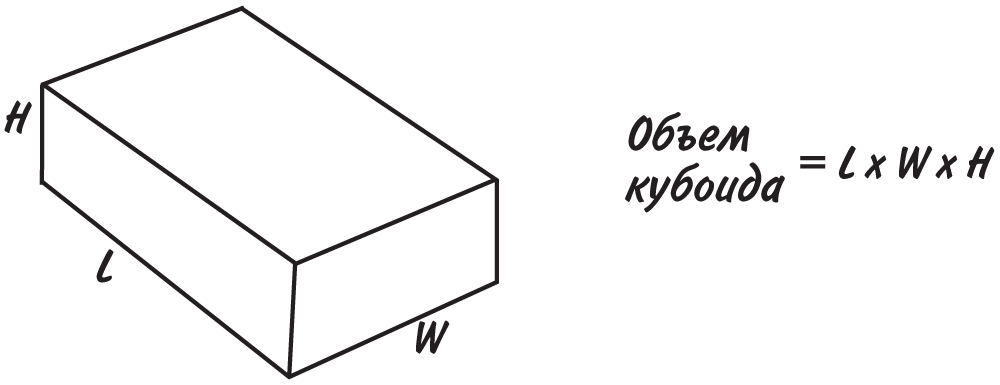
В повседневной жизни, кроме объема кубоида, вам, возможно, еще пригодится умение вычислять объем цилиндра, но для этого сперва следует познакомиться с числом π.
Окружность и π
Граница круга называется окружностью, отрезок между противоположными точками окружности, проходящий через центр круга, — диаметром, а расстояние от центра до окружности — радиусом, и все эти величины связаны между собой посредством числа π. Эта греческая буква называется «пи» и обозначает особое число, которое получится в результате деления длины любой окружности на ее диаметр.
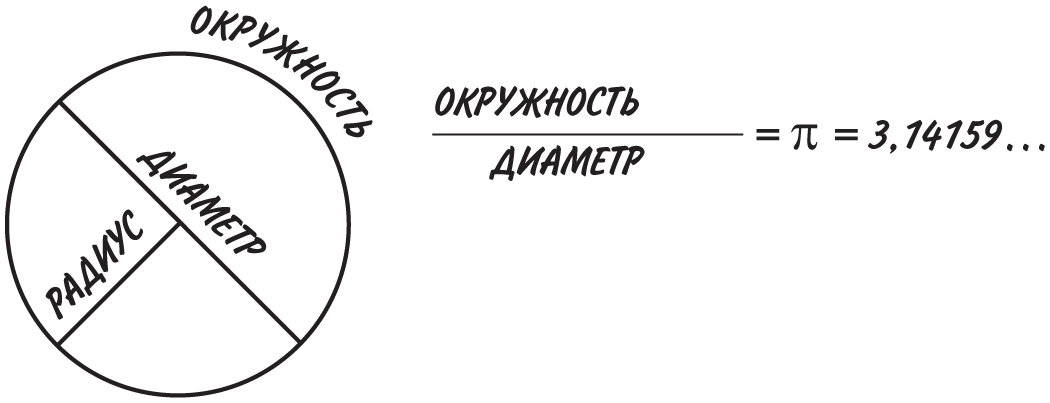
Эта десятичная дробь бесконечна, поэтому нам достаточно запомнить ее как 3,14, или 22/7. Число π нужно для расчета площади круга, а также объемов цилиндра и сферы.
В поисках π
Число π с давних пор занимает людские умы, поскольку его очень сложно точно рассчитать. Древнегреческий математик Архимед начертил близкую к окружности фигуру с 96 миниатюрными сторонами и с ее помощью вычислил, что значение π лежит где-то между 3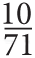 и 3
и 3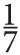 , то есть получил π с точностью до 0,001.
, то есть получил π с точностью до 0,001.
В XVI веке голландский математик Людольф ван Цейлен использовал фигуру с более чем 32 миллиардами сторон, потратив двадцать лет жизни на поиски первых 35 знаков числа π после запятой. Вероятно, он считал, что дальше этого зайти никому не удастся, но сразу после его смерти Исаак Ньютон и другие ученые обнаружили менее сложные способы получения еще большего количества знаков. В наши дни с помощью компьютеров найдены триллионы десятичных знаков π, но даже это лишь капля в море...
Основные формулы для круга таковы.
диаметр = 2 × радиус (обычно записывается как d = 2r)
длина окружности = π × диаметр (c = πd или c = 2πr)
площадь круга = πr2
Помните врезку о кратчайших расстояниях? Если взлететь с Северного полюса и, обогнув Землю, приземлиться на Южном полюсе, расстояние перелета составит 20 000 км. А какой будет длина подземного хода, ведущего с одного полюса на другой через центр Земли?
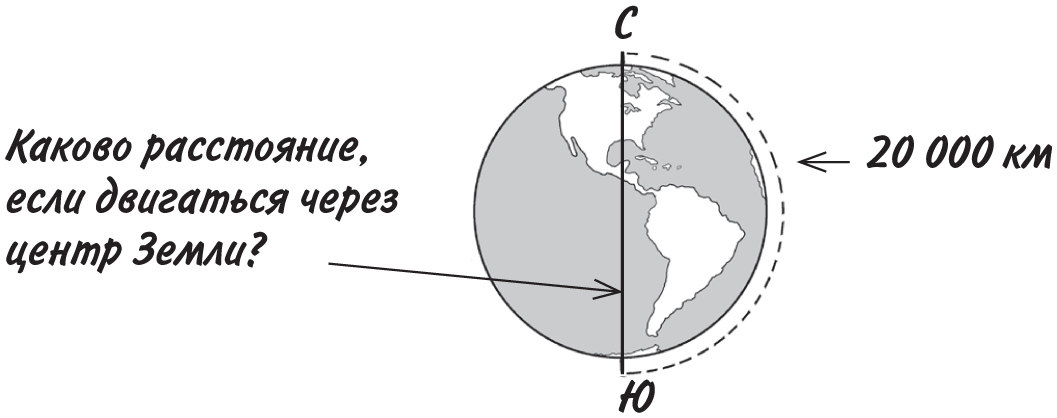
Нам известно, что 20 000 км — это половина пути вокруг Земли, значит, полная длина окружности составит 2 × 20 000 = 40 000 км. Путь через центр — диаметр d; воспользуемся формулой c = πd. Мы знаем, что π × d = 40 000. Следовательно, d = 40 000 ÷ π = 12 732 км.
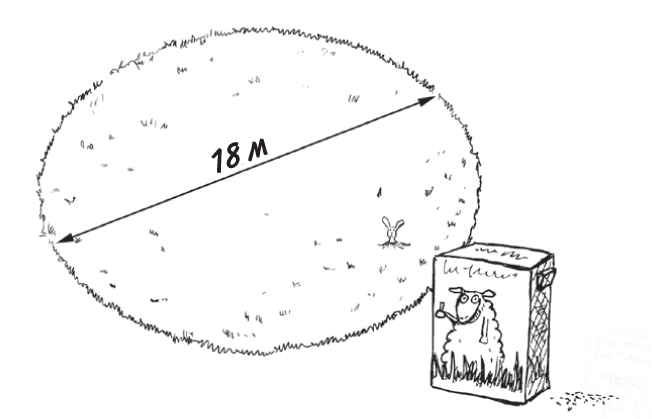
Давайте перейдем к более насущным вопросам. Допустим, вы решили засеять травой круглый газон шириной 18 м. Одной упаковки семян хватает на 10 м2. Сколько всего понадобится упаковок? Нам нужно вычислить площадь газона, поэтому воспользуемся формулой площадь круга = πr2. Мы знаем, что ширина газона составляет 18 м; по сути, это его диаметр. Следовательно, r = 18/2 = 9 м. Теперь можно рассчитать площадь: πr2 = π × r × r = π × 9 × 9 = π × 81 = 254 м2. Поскольку одной упаковки семян хватает на 10 м2, нам понадобится 254 ÷ 10 = 25,4 упаковки.
Цилиндр
Основная формула для расчета объема, куда входит число π, относится к цилиндру. Чтобы узнать его объем, нужно умножить площадь его основания (это круг) на высоту — или число π на квадрат радиуса на высоту.
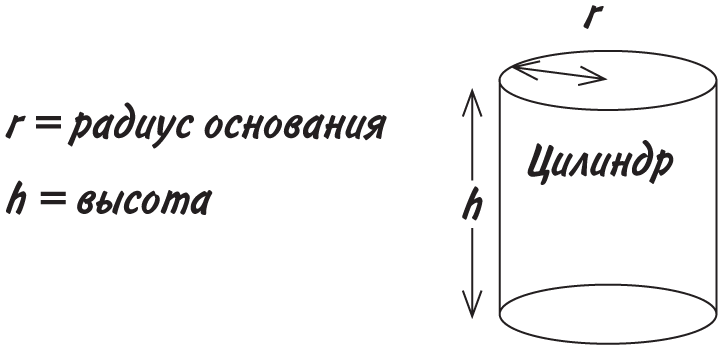
Объем цилиндра = πr2h
Предположим, вы зашли в строительный магазин и увидели огромную банку вашей любимой краски цвета подгоревшей яичницы. Вам стало интересно, а сколько краски она вмещает? Так как радиус измерить сложно, измерим ширину основания — получим диаметр 160 мм. Разделим его пополам и узнаем радиус: r = 160 ÷ 2 = 80 мм. Также измерим высоту — она равна 0,3 м.
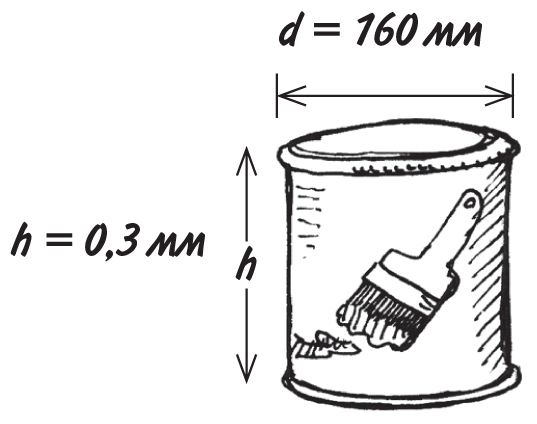
При расчете площади или объема всегда используйте одинаковые единицы измерения. У нас радиус в миллиметрах, а высота в метрах, так что будем считать все в метрах, чтобы в итоге получить кубические метры. Преобразуем радиус: 80 мм = 0,08 м. Теперь подставим r = 0,08 и h = 0,3 в формулу:
| объем банки | = π × (0,08)2 × 0,3 |
| = π × 0,0064 × 0,3 | |
| = 0,00603 м3 |
Заглянув в табличку в подразделе «Метры, литры и граммы», мы видим, что в 1 кубическом метре 1000 литров. Стало быть, наша таинственная банка вмещает 0,00603 × 1000 = 6,03 л.
Прежде мы выяснили, что нам нужно 6 банок краски объемом 750 мл для стен и еще 2 банки для потолка — всего 8 банок. Сколько это в литрах? 750 мл = 0,75 л, значит, в 8 банках 8 × 0,75 = 6 л. Отлично, одной огромной банки как раз хватит на все стены и потолок!
Быстрый способ
Если у вас есть рулетка, вы можете рассчитать объем цилиндра, не связываясь с числом π. Для этого нужно измерить его окружность с, диаметр d и высоту h. Длина окружности неявно вводит π в расчеты, и получается изумительно простая формула:
объем цилиндра = dch/4
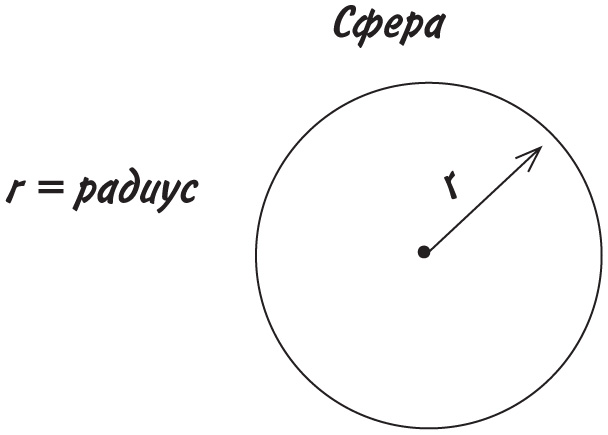
Сфера
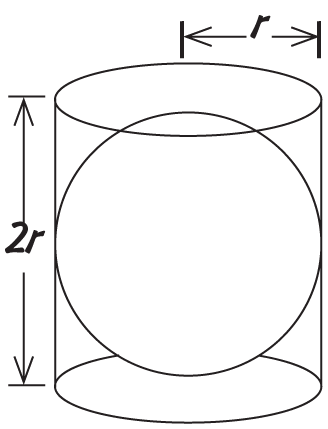
Около 2250 лет тому назад греческий ученый и математик Архимед совершил множество потрясающих открытий. Но лишь одно изображено на его могильной плите: Архимед был первым, кто доказал, что сфера, вписанная в цилиндр, занимает ровно 2/3 его объема. Иначе говоря, если взять банку с бобами в точности такого размера, чтобы в нее входил теннисный мяч, этот мяч вытолкнет наружу ровно 2/3 бобов. Благодаря Архимеду у нас теперь есть формула объема сферы.

Итак, возьмем сферу и обозначим ее радиус r.
Сначала выведем формулу объема наименьшего цилиндра, в который помещается эта сфера. Возьмем обычную формулу объема цилиндра πr2h, однако учитывая, что высота цилиндра в нашем случае равна 2r, объем наименьшего цилиндра будет πr2 × 2r = 2πr3.
Согласно Архимеду, сфера занимает 2/3 этого объема, следовательно, объем сферы = 2/3 × 2πr 3. В итоге получается:
объем сферы = 4/3 πr3
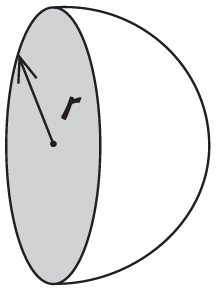
Раз уж мы занялись сферой, стоит упомянуть, что если разрезать ее пополам, площадь круга на срезе будет равна πr2. А площадь поверхности сферы вчетверо больше площади круга, поэтому
площадь поверхности сферы = 4πr2
Формула объема сферы — еще одна весьма популярная на уроках геометрии тема, совершенно бесполезная в обыденной жизни: скажите на милость, как измерить радиус чего-то вроде футбольного мяча относительно его центра? Гораздо проще измерить его окружность с и воспользоваться такой формулой:
объем сферы = с3/60
Если вы ученый-ракетостроитель и вам нужен более точный результат, то вычисляйте так:
объем сферы = с3/59,2176264
Однако если вы ракетостроитель и учите математику по этой книге, то у нас у всех серьезные проблемы, не так ли?
Пифагор и его теорема
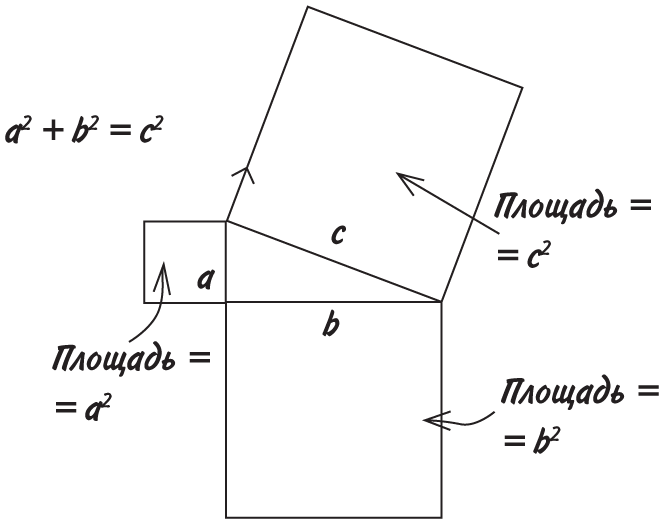
Пифагор жил примерно за 300 лет до Архимеда и прославился в первую очередь своей знаменитой теоремой: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.
Звучит несколько замысловато, но взгляните на рисунок, и вы все поймете. Если взять прямоугольный треугольник и пририсовать к каждой его стороне квадрат, то площади двух меньших квадратов в сумме будут равны площади большого квадрата.
Если вас беспокоит вопрос, зачем кому-то понадобилось лепить к сторонам треугольника квадраты, не волнуйтесь, польза теоремы не в этом. Лучше представьте, что вы по диагонали пересекаете футбольное поле. Если размер поля 100 м × 70 м, какое расстояние вам нужно преодолеть?
 Вычисления будут не совсем простыми, поэтому, получив ответ, стоит убедиться, что он правдоподобен! По рисунку видно, что результат должен быть больше 100 м, но меньше 170 м.
Вычисления будут не совсем простыми, поэтому, получив ответ, стоит убедиться, что он правдоподобен! По рисунку видно, что результат должен быть больше 100 м, но меньше 170 м.
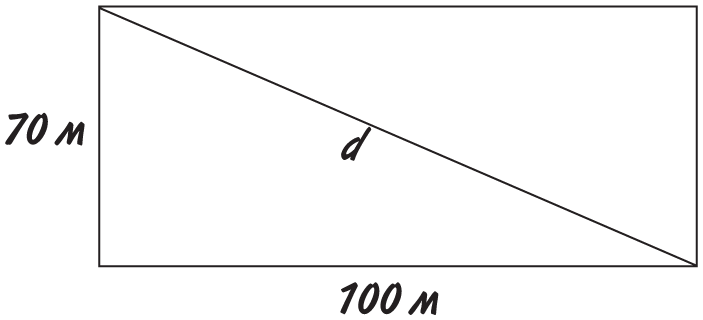
Обозначим диагональ буквой d.
Согласно теореме Пифагора, d2 = 1002 + 702
Вычисляем: d2 = 10 000 + 4900 = 14 900
Теперь нужно извлечь квадратный корень из 14 900. Иными словами, при умножении какого числа на само себя получится 14 900?
Если у вас нет калькулятора, самый простой способ извлечения корней — догадка и корректировка. Положим, вам кажется, что ответ может равняться 120, тогда считаем: 120 × 120 = 14 400. Довольно близко, но все же меньше, чем надо. Ладно, попробуем 123 × 123 = 15 129. Выходит больше, чем 14 900. Проверим еще один вариант 122 × 122 = 14 884. Уже совсем рядышком, однако теперь все же посчитаем на калькуляторе.
 Введите <14900 √> и получите 122,065.
Введите <14900 √> и получите 122,065.
Значит, искомое расстояние чуть больше 122 м.
За более чем 2500 лет, прошедших со времени доказательства Пифагором этой теоремы, люди придумали не менее 300 других ее доказательств, основанных на сложных алгебраических вычислениях, чертежах и тригонометрии, а также следующий способ, где достаточно лишь посмотреть на несколько фигур:
Докажем, что a2 + b2 = c2
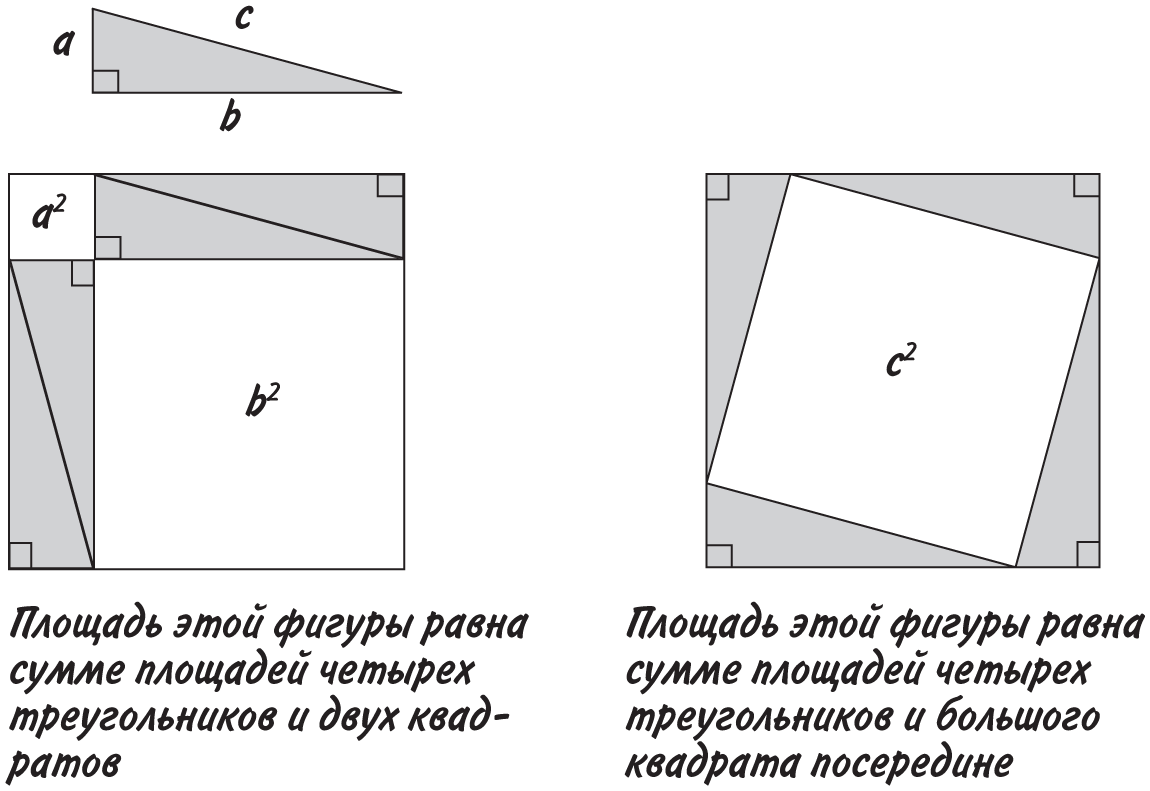
Внешние контуры обеих нижних фигур — это квадраты с длиной сторон (a + b). Это означает, что их площади равны и, следовательно, если из квадратов со стороной (a + b) вычесть площади четырех равных треугольников, то сумма площадей двух меньших квадратов будет равна площади большого квадрата. Вот мы и доказали, что a2 + b2 = c2!

