ПРОДВИНУТАЯ МАТЕМАТИКА

Итак, вы добрались почти до конца книги: поздравляю! Как насчет того, чтобы блеснуть интеллектом и доказать, что вам по зубам и более сложные теоретические штучки? Следующие два раздела посвящены математическим понятиям, которые вам вряд ли пригодятся в обыденной жизни, но с ними интересно в общих чертах ознакомиться, особенно если в школьные годы они являлись вам в кошмарах!

Углы, треугольники и тригонометрия

Угол между двумя пересекающимися линиями измеряют в градусах, обозначая их маленьким символом °. Если хотите посмот­реть, какого примерно размера угол в 1°, возьмите длинную нитку, сложите ее пополам, проденьте в петлю большой палец и вытяните руку в сторону. Другой рукой возьмите концы нитки и держите их перед собой так, чтобы нитка была натянута. Угол в месте схождения двух концов и составит около 1°.

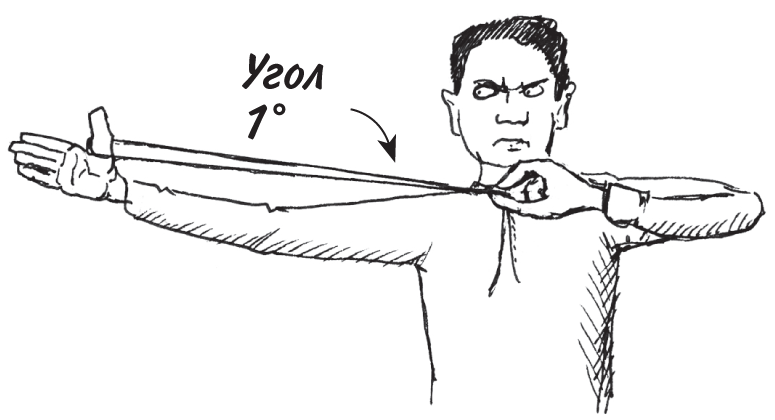
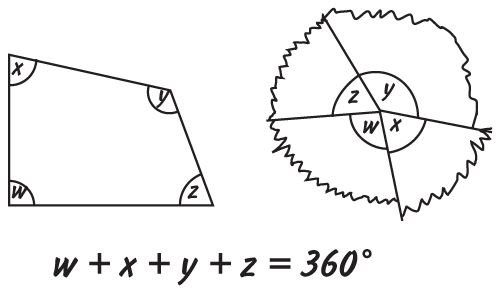
Угол между сторонами квадрата равен 90° и называется прямым. Если вы сделаете полный поворот вокруг своей оси, вы повернетесь на 360°. Угол в 180° представляет собой прямую линию; а сумма углов любого треугольника всегда будет 180°. Вырежте треугольник из бумаги, оторвите его уголки и, сложив их вместе, получите прямую линию, как показано на рисунке ниже.

Четыре угла любого четырехугольника вместе составляют 360°, так что если их оторвать и сложить, они сойдутся один к одному без зазора.

Возможно, у вас есть калькулятор с кучей таинственных кнопок, которыми вы не пользуетесь? Это обидно, учитывая, что вы за них заплатили, так что давайте вкратце рассмотрим, что такое синус, косинус и тангенс.

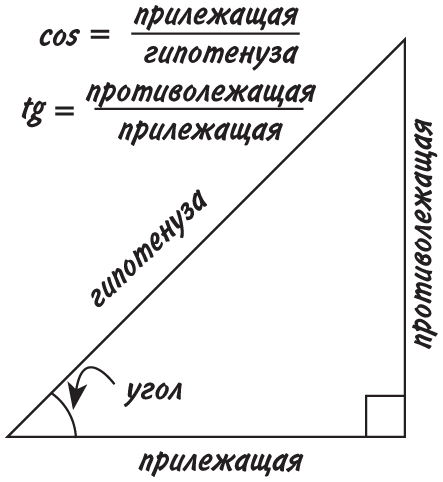
Основная идея состоит в том, что если вы знаете длину только одной (или двух) стороны треугольника и его углы, то, воспользовавшись тригонометрией, можете вычислить то, что неизвестно. Проще всего иметь дело с прямоугольными треугольниками, поскольку достаточно знать длину одной из сторон и величину любого угла (помимо прямого), чтобы вычислить его остальные параметры.

Допустим, известна величина одного из углов; если взять сторону, противолежащую этому углу, и разделить на самую длинную сторону, то есть гипотенузу, получится дробь, которая называется синусом угла и обозначается словом sin. (Пишется точно так же, как английское sin, то есть «грех», но не спешите радоваться — порок и разврат здесь ни при чем.)

Предположим, вы пытаетесь достать свой любимый ботинок из водосточного желоба (бог знает, как он туда попал, но, сами понимаете, всякое бывает). В вашем распоряжении 8-метровая лестница, стоящая у стены здания.

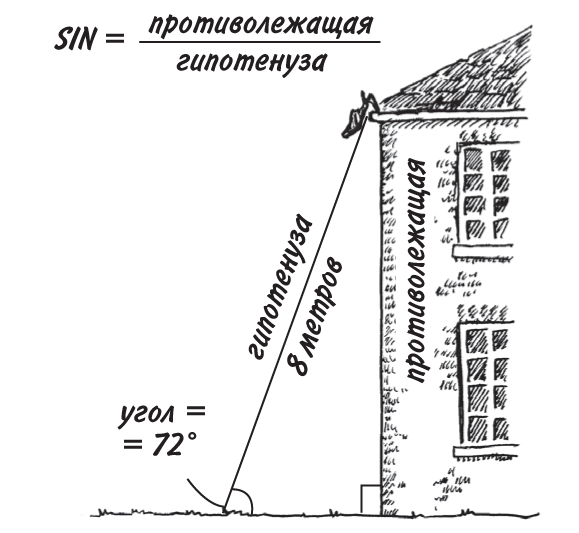
Лестница, стена и поверхность земли образуют прямоугольный треугольник. Если вы измерили угол между лестницей и землей (он равен 72°), то можете вычислить, на какой высоте находится желоб, чтобы не теряться, отвечая потом на вопросы работников скорой помощи.

Лестница является гипотенузой треугольника, и она равна 8. Высота, которую мы хотим узнать, — это сторона, противо­лежащая углу в 72°, так что можем составить простое уравнение:

sin 72° = противолежащая сторона/8

Умножив обе части уравнения на 8, получим

sin 72° × 8 = противолежащая сторона

Чтобы вычислить синус на калькуляторе, введите <sin 72 => и получите 0,951.

Затем умножим это число на 8 — выйдет 7,608. Это и есть высота от земли до желоба в метрах!

Косинус (cos) и тангенс (tg) — это дроби, представляющие отношения других сторон треугольника друг к другу.

И это практически все, что вам нужно знать о тригоно­метрии...

Логарифм: это что за чертовщина?

Всякий раз, когда разговор заходит о самых мрачных и зловещих тайнах математики, как правило, вспоминают о логарифмах. На многих это слово навевает кошмары, полные бессмысленных чисел и язвительных учителей. Однако теперь, когда школа позади, не пора ли все же разобраться, что это такое? Не будет ни тестов, ни контрольных, ни летающих губок для вытирания доски — чудовище не сможет вам навредить.

Логарифмы в 1645 году изобрел шотландец Джон Непер, и на протяжении 350 лет (пока не изобрели калькуляторы) они были единственным верным средством для быстрого умножения и деления очень больших чисел. Так в чем же суть логарифмов?

Возьмем весьма простое выражение:

1000 × 100 = 100 000

Иначе его можно записать как 10³ × 10² = 10⁵ — это абсолютно то же самое, однако вместо того, чтобы перемножать большие числа, мы просто сложили степени: 3 + 2 = 5. Джон Непер понял, что любое число можно представить в виде степени числа 10, после чего для умножения или деления чисел достаточно лишь складывать или вычитать их степени.

Но вот незадача: такие степени редко бывают красивыми ровными числами, например 78 = 10^1,89209. Когда степени становятся затейливыми десятичными дробями, их называют логарифмами. Поскольку 78 = 10^1,89209, можно сказать, что логарифм от 78 равен 1,89209.

Перевод чисел в логарифмы — крайне утомительный процесс, но соратник Непера по имени Генри Бригс облечил его, разработав для подобных преобразований так называемые логарифмические таблицы. Некоторые из таблиц позволяли получить лишь три знака после запятой: 78 = 10^1,892. А по наиболее точным таблицам Бригса выходило, что 78 = 10^{1,89209460269048}. Соответственно, чем точнее логарифмы, тем точнее результат вычислений. (Исаак Ньютон, изучая движения звезд и планет, дошел в вычислении логарифма до 50 знаков после запятой, но его увлеченность граничила с манией.)

Что ж, опробуем логарифмы в деле.

Точный ответ = 1 198 366 848. Погрешность при вычислении с помощью логарифмов составила примерно 1 миллионную!

Отправить