ГЛАВА 7

ТЫ — ТО, НА ЧТО ТЫ ПОХОЖ

Фрэнк Абигнейл-младший — один из самых знаменитых мошенников в истории, Леонардо Ди Каприо сыграл его в фильме Спилберга «Поймай меня, если сможешь». Абигнейл подделывал чеки на миллионы долларов, прикидывался адвокатом и преподавателем колледжа, путешествовал по миру, выдавая себя за пилота Pan Am, и все это когда ему еще не исполнился 21 год. Но, наверное, самая сногсшибательная его проделка — это когда он в конце 1960-х почти год успешно изображал врача в Атланте. Казалось бы, чтобы заниматься медициной, нужно много лет учиться в медицинском институте, пройти ординатуру, получить лицензию и так далее, но Абигнейлу удалось обойти эти мелочи, и все были довольны.

Представьте на секунду, что вам предстоит провернуть нечто подобное. Вы тайком пробираетесь в пустой медицинский кабинет. Вскоре появляется пациент и рассказывает вам о своих симптомах. Надо поставить ему диагноз, только вот в медицине вы ничего не смыслите. В вашем распоряжении — шкаф с историями болезней: симптомы, диагнозы, назначенное лечение и так далее. Как вы поступите? Самое простое — это заглянуть в документы, поискать пациента с самыми похожими симптомами и поставить такой же диагноз. Если вы умеете вести себя с больным и убедительно говорить, как Абигнейл, этого может оказаться достаточно для успеха. Та же идея успешно применяется и за пределами медицины. Если вы молодой президент и столкнулись с мировым кризисом, как в свое время Кеннеди, когда самолет-разведчик обнаружил на Кубе советские ядерные ракеты, вполне вероятно, что готового сценария у вас не окажется. Вместо этого можно поискать похожие примеры в истории и попытаться сделать из них выводы. Объединенный комитет начальников штабов подталкивал президента напасть на Кубу, но Кеннеди только что прочитал The Guns of August — бестселлер о начале Первой мировой войны — и хорошо осознавал, что такой шаг легко может вылиться в тотальную войну. Кеннеди предпочел морскую блокаду — и, может быть, спас мир от ядерной катастрофы.

Аналогия была искрой, из которой разгорелись величайшие научные достижения в истории человечества. Теория естественного отбора родилась, когда Дарвин, читая An Essay on the Principle of Population («Опыт о законе народонаселения») Мальтуса, был поражен сходством между борьбой за выживание в экономике и в природе. Модель атома появилась на свет, когда Бор увидел в ней миниатюрную Солнечную систему, где электроны соответствовали планетам, а ядро — Солнцу. Кекуле открыл кольцевую форму молекулы бензола, представив себе змею, пожирающую свой хвост.

У рассуждений по аналогии выдающаяся интеллектуальная родословная. Еще Аристотель выразил их в своем законе подобия: если две вещи схожи, мысль об одной из них будет склонна вызывать мысль о другой. Эмпирики, например Локк и Юм, пошли по этому пути. Истина, говорил Ницше, — это движущаяся армия метафор. Аналогии любил Кант, а Уильям Джеймс полагал, что чувство одинаковости — киль и позвоночник человеческого мышления. Некоторые современные психологи даже утверждают, что чело­веческое познание целиком соткано из аналогий. Мы полагаемся на них, чтобы найти дорогу в новом городе и чтобы понять такие выражения, как «увидеть свет» и «не терять лица». Подростки, которые в каждое предложение вставляют словечко «типа», согласятся, типа, что аналогия — это, типа, важная штука.

С учетом всего этого неудивительно, что аналогия играет видную роль в машинном обучении. Однако дорогу себе она пробивала медленно, и поначалу ее затмевали нейронные сети. Первое воплощение аналогии в алгоритме появилось в малоизвестном отчете, написанном в 1951 году Эвелин Фикс и Джо Ходжесом — статистиками из Университета Беркли, — и потом десятки лет не публиковалось в мейнстримных журналах. Однако тем временем начали появляться, а потом множиться другие статьи об алгоритме Фикс и Ходжеса, пока он не стал одним из самых исследуемых в информатике. Алгоритм ближайшего соседа — так он называется — будет первым шагом в нашем путешествии по обучению на основе аналогий. Вторым станет метод опорных векторов, который, как буря, налетел на машинное обучение на пере­ломе тысячелетий и лишь недавно встретил достойного соперника в лице глубокого обучения. Третья и последняя тема — это полно­ценное аналогическое рассуждение, которое несколько десяти­летий было базовым в психологии и искусственном интеллекте и примерно столько же — в машинном обучении.

Аналогизаторы — наименее сплоченное из пяти «племен». В отличие от приверженцев других учений, которых объединяет сильное чувство идентичности и общие идеалы, аналогизаторы представляют собой скорее свободное собрание ученых, согласных с тем, что в качестве основы обучения нужно полагаться на суждения о сходстве. Некоторые, например ребята, занимающиеся методом опорных векторов, могут даже не захотеть встать под общий зонтик. Но за окном идет дождь из глубоких моделей, и мне кажется, действовать сообща им не повредит. Аналогия — одна из центральных идей в машинном обучении, и аналогизаторы всех мастей — ее хранители. Может быть, в грядущем десятилетии в машинном обучении будет доминировать глубокая аналогия, соединяющая в один алгоритм эффективность ближайшего соседа, математическую сложность метода опорных векторов и мощь и гибкость рассуждения по аналогии. (Вот я и выдал один из своих секретных научных проектов.)

Попробуй подобрать мне пару

Алгоритм ближайшего соседа — самый простой и быстрый обуча­ющийся алго­ритм, какой только изобрели ученые. Можно даже сказать, что это вообще самый быстрый алгоритм, который можно придумать. В нем не надо делать ровным счетом ничего, и поэтому для выполнения ему требуется нулевое время. Лучше не бывает. Если вы хотите научиться узнавать лица и в вашем распоряжении есть обширная база данных изображений с ярлыками «лицо / не лицо», просто усадите этот алгоритм за работу, расслабьтесь и будьте счастливы. В этих изображениях уже скрыта модель того, что такое лицо. Представьте, что вы Facebook и хотите автоматически определять лица на фотографиях, которые загружают пользователи, — это будет прелюдией к автоматическому добавлению тегов с именами друзей. Будет очень приятно ничего не делать, учитывая, что ежедневно в Facebook люди загружают свыше трехсот миллионов фотографий. Применение к ним любого из алгоритмов машинного обучения, которые мы до сих пор видели (может быть, кроме наивного байесовского), потребовало бы массы вычислений. А наивный Байес недостаточно сообразителен, чтобы узнавать лица.

Конечно, за все надо платить, и цена в данном случае — это время проверки. Джейн Юзер только что загрузила новую картинку. Это лицо или нет? Алгоритм ближайшего соседа ответит: найди самую похожую картинку во всей базе данных маркированных фотографий — ее «ближайшего соседа». И если на найденной картинке лицо, то и на этой тоже. Довольно просто, но теперь придется за долю секунды (в идеале) просканировать, возможно, миллиарды фотографий. Алгоритм застают врасплох, и, как ученику, который не готовился к контрольной, ему придется как-то выходить из положения. Однако в отличие от реальной жизни, где мама учит не откладывать на завтра то, что можно сделать сегодня, в машинном обучении прокрастинация может принести большую пользу. Вообще говоря, всю область, в которую входит алгоритм ближайшего соседа, называют «ленивым обучением», и в таком термине нет ничего обидного.

Ленивые обучающиеся алгоритмы намного умнее, чем может показаться, потому что их модели, хотя и неявные, могут быть невероятно сложными. Давайте рассмотрим крайний случай, когда для каждого класса у нас есть только один пример. Допустим, мы хотим угадать, где проходит граница между двумя государствами, но знаем мы только расположение их столиц. Большинство алгоритмов машинного обучения зайдет здесь в тупик, но алго­ритм ближайшего соседа радостно скажет, что граница — это прямая линия, лежащая на полпути между двумя городами.

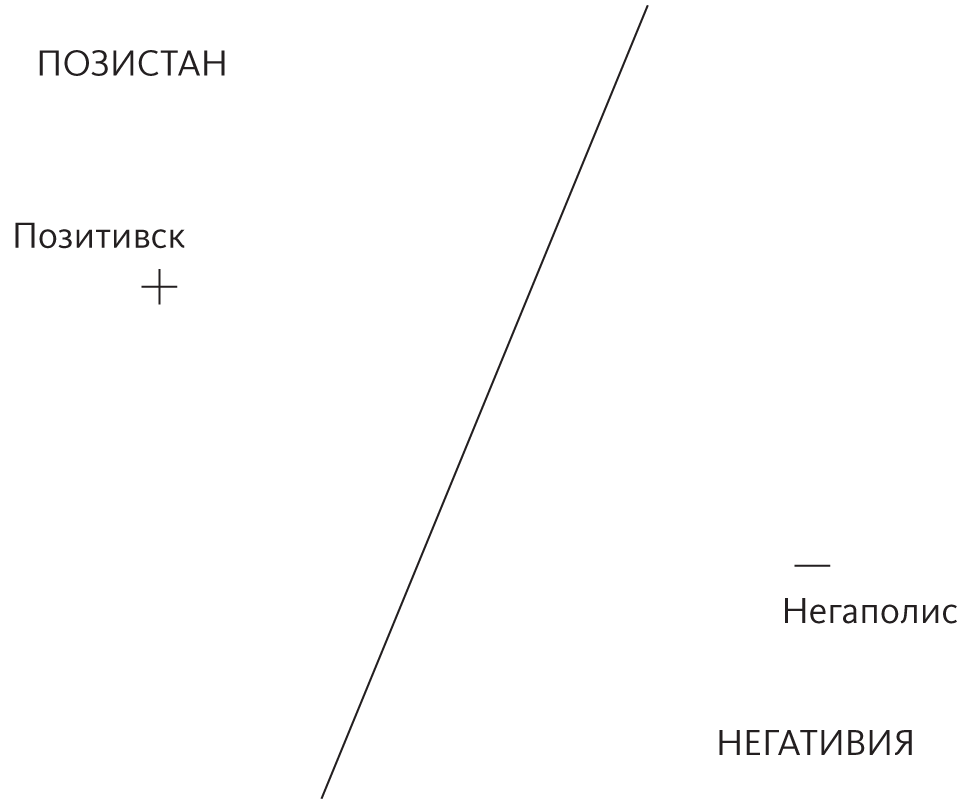
Точки на этой линии находятся на одинаковом удалении от обоих столиц. Точки слева от нее ближе к Позитивску, поэтому ближайший сосед предполагает, что они относятся к Позистану, и наоборот. Конечно, если бы это была точная граница, нам бы крупно повезло, но и это приближение, вероятно, намного лучше, чем ничего. Однако по-настоящему интересно становится, когда мы знаем много городов по обеим сторонам границы:

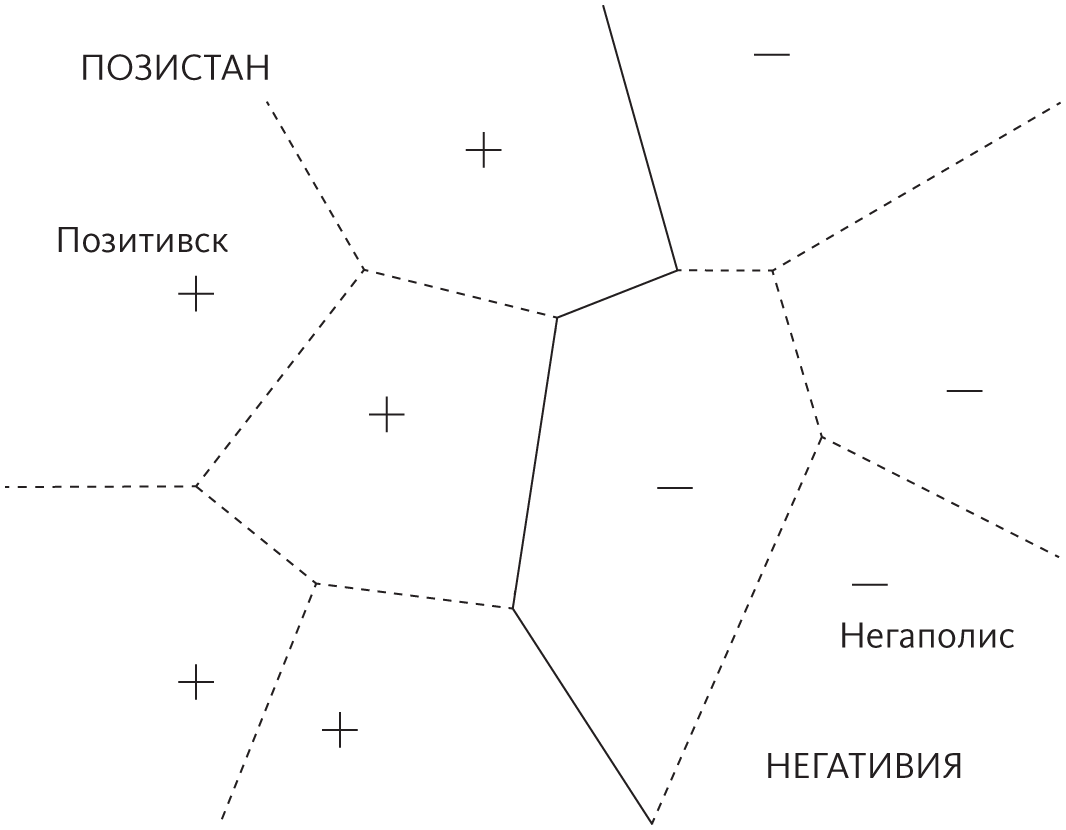
Ближайший сосед способен провести очень сложную границу, хотя он просто запоминает, где находятся города, и в соответствии с этим относит точки к тому или иному государству. «Агломерацией» города можно считать все точки, которые к нему ближе, чем к любому другому. Границы между такими агломерациями показаны на рисунке пунктиром. Теперь и Позистан, и Негативия — просто объединение агломераций всех городов этих стран. В отличие от этого алгоритма, деревья решений (например) способны лишь проводить границы, проходящие попеременно с севера на юг и с востока на запад, что, вероятно, будет намного худшим приближением настоящей границы. Таким образом, хотя алгоритмы на основе дерева решений будут изо всех сил стараться за время обу­чения определить, где проходит граница, победит «ленивый» метод ближайшего соседа.

Все дело в том, что построить глобальную модель, например дерево решений, намного сложнее, чем просто одно за другим определить положение конкретных элементов запроса. Представьте себе попытку определить с помощью дерева решений, что такое лицо. Можно было бы сказать, что у лица два глаза, нос и рот, но что такое глаз и как его найти на изображении? А если человек закроет глаза? Дать надежное определение лица вплоть до отдельных пикселей крайне сложно, особенно учитывая всевозможные выражения, позы, контекст, условия освещения. Алгоритм ближайшего соседа этого не делает и срезает путь: если в базе данных изображение, больше всего похожее на то, которое загрузила Джейн, — это лицо, значит на загруженном изображении тоже лицо. Чтобы все работало, в базе данных должна найтись достаточно похожая картинка, например лицо в аналогичном положении, освещении и так далее, поэтому чем больше база данных, тем лучше. Для простой двухмерной проблемы, например угадывания границы между двумя странами, маленькой базы данных будет достаточно. Для очень сложной проблемы, например определения лиц, где цвет каждого пикселя — это измерение вариативности, понадобится огромная база данных. Сегодня такие базы существуют. Обучение с их помощью может быть слишком затратным для трудолюбивых алгоритмов, которые явно проводят границу между лицами и не-лицами, однако для ближайшего соседа граница уже скрыта в расположении точек данных и расстояниях, и единственная затрата — это время запроса.

Та же идея создания локальной модели вместо глобальной работает и за пределами проблем классификации. Ученые повсеместно используют линейную регрессию для прогнозирования непрерывных переменных, несмотря на то что большинство явлений нелинейны. К счастью, явления линейны локально, потому что гладкие кривые локально хорошо аппроксимируются прямыми линиями. Поэтому не пытайтесь подобрать прямую ко всем данным — сначала подгоните ее к точкам рядом с точкой запроса: получится очень мощный алгоритм нелинейной регрессии. Лень оправдывает себя. Если бы Кеннеди захотел получить полную теорию международных отношений, чтобы решить, что делать с ракетами на Кубе, у него были бы проблемы. Но он увидел аналогию между кризисом и ситуацией перед Первой мировой войной, и эта аналогия направила его к правильным решениям.

Как поведал Стивен Джонсон в книге The Ghost Map, алгоритм ближайшего соседа может спасать жизни. В 1854 году Лондон поразила вспышка холеры. В некоторых частях города от нее умер каждый восьмой житель. Господствовавшая тогда теория, что холера вызвана якобы плохим воздухом, не помогла предотвратить распространение эпидемии. Но Джон Сноу, физик, скептически относившийся к этой теории, придумал кое-что получше. Он отметил на карте Лондона все известные случаи холеры и разделил карту на области, расположенные ближе всего к общественным водокачкам. Эврика! Оказалось, что почти все смерти приходились на «агломерацию» конкретного водозабора, расположенного на Брод-стрит в районе Сохо. Сделав вывод, что вода там заражена, Сноу убедил местные власти выключить насос, и эпидемия сошла на нет. Из этого случая родилась эпидемиология, а еще это пример первого успешного применения алгоритма ближайшего соседа — почти за столетие до его официального открытия.

В алгоритме ближайшего соседа каждая точка данных — это маленький классификатор, предсказывающий класс для всех примеров запросов, на которые она правильно отвечает. Это как армия муравьев: отдельные солдаты сами по себе делают немного, но вместе способны сдвигать горы. Если груз слишком тяжел для одного муравья, он зовет соседей. Метод k-ближайших соседей действует в том же духе: тестовый пример классифицируется путем нахождения k-ближайших соседей, которые после этого голосуют. Если ближайшее изображение к только что загруженному — это лицо, но следующие два ближайших — нет, третий ближайший сосед решает, что загруженная картинка все же не лицо. Алгоритм ближайшего соседа подвержен переобучению: если точке данных присвоен неправильный класс, он распространится на всю свою агломерацию. Алгоритм k-ближайших соседей более устойчив, потому что ошибается только тогда, когда большинство из k-ближайших соседей зашумлены. Но за это приходится платить более замутненным зрением: из-за голосования размываются мелкие детали границы. Когда k идет вверх, дисперсия уменьшается, но увеличивается смещенность.

Брать k-ближайших соседей вместо одного — это еще не все. Интуиция подсказывает, что примеры, ближе всего расположенные к тесто­вому, должны быть важнее. Это ведет нас к взвешенному алго­ритму k-ближайших соседей. В 1994 году группа ученых из Миннесот­ского университета и Массачусетского технологического института построила рекомендательную систему на основе, по их словам, «обманчиво простой идеи»: люди, которые соглашались на что-то в прошлом, с большей вероятностью согласятся на это и в будущем. Эта мысль вела прямиком к системам коллаборативной фильтрации, которые имеются на всех уважающих себя сайтах электронной торговли. Представьте, что вы, как Netflix, собрали базу данных, где каждый пользователь присваивает просмотренным фильмам рейтинг от одной до пяти звезд. Вы хотите определить, понравится ли вашему пользователю по имени Кен фильм «Гравитация», поэтому ищете пользователей, оценки которых лучше всего коррелируют с оценками Кена. Если все они присвоили «Гравитации» высокий рейтинг, вероятно, так поступит и Кен, и этот фильм можно ему посоветовать. Если, однако, у них нет единого мнения в отношении «Гравитации», все равно нужно как-то выйти из положения, и в данном случае пригодится список пользователей, упорядоченный по их корреляции с Кеном. Если Ли коррелирует с Кеном сильнее, чем Мег, его оценки должны считаться, соответственно, более важными. Спрогнозированная оценка Кена будет таким образом средней взвешенной оценок его соседей, где вес каждого соседа — это его коэффициент корреляции с Кеном.

Однако есть интересный момент. Представьте, что у Ли и Кена очень схожие вкусы, но, когда Кен дает фильму пять звездочек, Ли всегда выставляет три, когда Кен дает три, Ли — только одну и так далее. Нам хотелось бы использовать оценки Ли для прогнозирования оценок Кена, но, если сделать это «в лоб», мы всегда будем отклоняться на две звездочки. Вместо этого нужно предсказать, насколько рейтинги Кена будут выше или ниже его средней, основываясь на таком же показателе для Ли. Теперь видно, что Кен всегда на две звездочки выше своей средней, когда Ли на две звездочки выше своей, и наш прогноз будет попадать в точку.

Кстати говоря, для коллаборативной фильтрации явные оценки не обязательны. Если Кен заказал фильм на Netflix, это значит, что он ожидает, что фильм ему понравится. Так что «оценкой» может быть просто «заказал / не заказал», и два пользователя будут похожи, если они заказывают много одинаковых фильмов. Даже простой клик на что-то косвенно показывает интерес пользователя. Алгоритм ближайшего соседа работает во всех этих случаях. Сегодня для того, чтобы давать рекомендации посетителям сайта, используются все виды алгоритмов, но взвешенный k-ближайший сосед был первым, нашедшим широкое применение в этой области, и его до сих пор сложно победить.

Рекомендательные системы — это большой бизнес: Amazon они дают треть доходов, а Netflix — три четверти. А ведь когда-то метод ближайшего соседа считался непрактичным из-за высоких требований к памяти. В те времена память компьютеров делали из маленьких сердечников, напоминавших железные кольца, по одному для каждого бита, и хранение даже нескольких тысяч примеров было обременительно. Сейчас времена изменились. Тем не менее не всегда целесообразно запоминать все увиденные примеры, а затем искать среди них, особенно потому что большинство из них, вероятно, не имеют отношения к делу. Еще раз взгляните на карту Позистана и Негативии и обратите внимание, что, если Позитивск исчез­нет, граница с Негативией не изменится: агломерации близлежащих городов расширятся и займут земли, которые занимала столица, но все они позистанские. Города, которые имеют значение, располагаются исключительно вдоль границы, поэтому все остальные можно опустить. Из этого вытекает простой способ повысить эффективность метода ближайшего соседа: нужно удалить примеры, которые были правильно классифицированы их соседями. Благодаря этому и другим приемам методы ближайшего соседа находят применение в самых неожиданных областях, например в управлении манипулятором робота в реальном времени. Но при этом в таких областях, как высоко­частотный трейдинг, где компьютеры покупают и продают ценные бумаги в доли секунды, такие методы по-прежнему не в почете. В гонке между нейронными сетями, которые можно применять к примерам с фиксированным количеством сложений, умножений и сигмоид, и алгоритмом, который должен искать ближайшего соседа в большой базе данных, нейронная сеть обязательно победит.

Другая причина, по которой исследователи поначалу скептически относились к ближайшему соседу, заключается в том, что было непонятно, может ли он определять истинные границы между понятиями. Но в 1967 году ученые-информатики Том Кавер и Питер Харт доказали, что при наличии достаточного количества данных ближайший сосед в худшем случае подвержен ошибкам всего в два раза больше, чем лучший вообразимый классификатор. Если, скажем, как минимум один процент тестовых примеров неизбежно будет неправильно классифицирован из-за зашумленности данных, ближайший сосед гарантированно получит максимум два процента ошибок. Это было историческое открытие. До этого момента все известные классификаторы исходили из того, что граница имеет очень четкую форму, обычно прямую линию. Это давало и плюсы, и минусы: с одной стороны, можно было доказать правильность, как в случае с перцептроном, но при этом появлялись строгие ограничения на то, что такой классификатор может узнать. Метод ближайшего соседа был первым в истории алгоритмом, который мог воспользоваться преимуществом неограниченного количества данных, чтобы обучаться произвольно сложным понятиям. Человеку не под силу проследить границы, которые он образует в гиперпространстве из миллионов примеров, но благодаря доказательству Кавера и Харта мы знаем, что они, вероятно, недалеки от истины. Рэй Курцвейл считает, что сингулярность начинается, когда люди перестают понимать, что делают компьютеры. По этому стандарту не совсем преувеличением будет сказать, что это уже происходит и началось еще в 1951 году, когда Фикс и Ходжес изобрели метод ближайшего соседа — самый маленький алгоритм, какой только можно изобрести.

Проклятие размерности

Конечно, в райском саду есть и Змей. Его зовут Проклятие Размерности, и, хотя он в большей или меньшей степени поражает все алгоритмы машинного обучения, для ближайшего соседа он особенно опасен. В низких измерениях (например, двух или трех) ближайший сосед обычно работает довольно хорошо, но по мере увеличения количества измерений все довольно быстро начинает рушиться. Сегодня нет ничего необычного в обучении на тысячах или даже миллионах атрибутов. Для коммерческих сайтов, пытающихся узнать ваши предпочтения, атрибутом становится каждый клик. То же самое с каждым словом на веб-странице, с каждым пикселем в изображении. А у ближайшего соседа проблемы могут появиться даже с десятками или сотнями атрибутов. Первая проблема в том, что большая часть атрибутов не имеет отношения к делу: можно знать миллион фактов о Кене, но, вполне возможно, лишь немногие из них могут что-то сказать (например) о его риске заболеть раком легких. Для конкретно этого предсказания критически важно знать, курит Кен или нет, а информация о курении вряд ли поможет решить, понравится ли ему «Гравитация». Символистские методы со своей стороны довольно хорошо убирают неподходящие атрибуты: если в атрибуте не содержится информация о данном классе, его просто не включают в дерево решений или набор правил. Но метод ближайшего соседа неподходящие атрибуты безнадежно запутывают, потому что все они вносят свой вклад в сходство между примерами. Если не имеющих отношения к делу атрибутов будет достаточно много, случайное сходство в нерелевантных измерениях подавит имеющее значение сходство в важных, и метод ближайшего соседа окажется ничем не лучше случайного угадывания.

Еще одна большая и неожиданная проблема заключается в том, что большое число атрибутов может мешать, даже когда все они имеют отношение к делу. Может показаться, что много информации — это всегда благо. Разве это не лозунг нашего времени? Но по мере увеличения числа измерений начинает экспоненциально расти число обучающих примеров, необходимых для определения границ понятия. Двадцать булевых атрибутов дадут примерно миллион возможных примеров. С двадцать первым примеров станет два миллиона, с соответствующим числом способов прохождения между ними границы. Каждый лишний атрибут делает проблему обучения в два раза сложнее, и это если атрибуты булевы. Если атрибут высокоинформативный, польза от его добавления может превышать затраты. Но когда в распоряжении есть лишь малоинформативные атрибуты, например слова в электронном письме или пиксели изображения, это, вероятно, породит проблемы, несмотря на то что в совокупности они могут нести достаточно информации, чтобы предсказать то, что вы хотите.

Все даже хуже. Ближайший сосед основан на нахождении схожих объектов, а в высоких измерениях распадается сама идея сходства. Гипер­пространство — как сумеречная зона. Наша интуиция, основанная на опыте жизни в трех измерениях, там не действует, и начинают происходить все более и более странные вещи. Представьте себе апельсин: шарик вкусной мякоти, окруженный тонкой кожицей. Мякоть в апельсине занимает, скажем, 90 процентов радиуса, а оставшиеся десять приходятся на кожуру. Это означает, что 73 процента объема апельсина — это мякоть (0,9³). Теперь рассмотрим гиперапельсин: если мякоть занимает все те же 90 процентов радиуса, но, скажем, в сотне измерений, то она сократится примерно до всего лишь 3⁄1000 процента объема (0,9¹⁰⁰). Гиперапельсин будет состоять из одной кожуры, и его никогда нельзя будет очистить!

Беспокоит и то, что происходит с нашей старой знакомой, гауссовой кривой. Нормальное распределение говорит, что данные в сущности расположены в какой-то точке (средняя распределения), но с некоторым расхождением вокруг нее (заданным стандартным отклонением). Верно? Да, но не в гиперпространстве. При нормальном распределении в высокой размерности будет выше вероятность получить пример далеко от средней, чем близко к ней. Кривая Гаусса в гиперпространстве больше похожа на пончик, чем на колокол. Когда ближайший сосед входит в этот беспорядочный мир, он безнадежно запутывается. Все примеры выглядят одинаково схожими и при этом слишком далеко отстоят друг от друга, чтобы делать полезные прогнозы. Если случайным образом равномерно рассеять примеры внутри высокоразмерного гиперкуба, большинство окажется ближе к грани этого куба, чем к своему ближайшему соседу. На средневековых картах неисследованные области обозначали драконами, морскими змеями и другими фантастическими существами или просто фразой «Здесь драконы». В гиперпространстве драконы повсюду, в том числе прямо в дверях. Попробуйте прогуляться в гости к соседу, и вы никогда туда не доберетесь: станете вечно блуждать в чужих землях и гадать, куда делись все знакомые предметы.

Деревья решений тоже не застрахованы от проклятия размерности. Скажем, понятие, которое вы пытаетесь получить, представляет собой сферу: точки внутри нее положительные, а снаружи — отрицательные. Дерево решений может приблизить сферу самым маленьким кубом, в который она помещается. Это не идеально, но и не очень плохо: неправильно классифицированы будут только углы. Однако в большем числе измерений почти весь объем гиперкуба окажется вне гиперсферы, и на каждый пример, который вы правильно классифицируете как положительный, будет приходиться много отрицательных, которые вы сочтете положительными, а это резко снижает точность.

На самом деле такая проблема есть у всех обучающихся алгоритмов — это вторая беда машинного обучения после переобучения. Термин «проклятие размерности» был придуман в 50-е годы Ричардом Беллманом, специалистом по теории управления. Он заметил, что алгоритмы управления, которые хорошо работают в трех измерениях, становятся безнадежно неэффективными в пространствах с большим числом измерений, например, когда вы хотите контролировать каждый сустав манипулятора или каждую ручку на химическом комбинате. А в машинном обучении проблема не только в вычислительных затратах: с ростом размерности само обучение становится все сложнее и сложнее.

Тем не менее не все потеряно. Во-первых, можно избавиться от не имеющих отношения к делу измерений. Деревья решений делают это автоматически, путем вычисления информационного выигрыша от каждого атрибута и выбора самых информативных. В методе ближайшего соседа мы можем сделать нечто похожее, сначала отбросив все атрибуты, которые дают прирост информации ниже определенного порога, а затем измерив схожесть в пространстве с меньшим числом измерений. В некоторых случаях это быстрый и достаточно хороший прием, но, к сожалению, ко многим понятиям он неприменим. Среди них, например, исключающее ИЛИ: если атрибут говорит что-то о данном классе только в сочетании с другими атрибутами, он будет отброшен. Более затратный, но хитрый вариант — «обернуть» выбор атрибута вокруг самого обучающегося алгоритма с поиском путем восхождения на выпуклые поверхности, который будет удалять атрибуты, пока это не повредит точности метода ближайшего соседа на скрытых данных. Ньютон многократно выбирал атрибуты и определил, что для предсказания траектории тела важна только его масса, а не цвет, запах, возраст и миллиард других свойств. Вообще говоря, самое важное в уравнении — все те количества, которые в нем не появляются: когда известны самые существенные элементы, часто оказывается легче разобраться, как они зависят друг от друга.

Одно из решений проблемы неважных атрибутов — определение их веса. Вместо того чтобы считать сходство по всем измерениям равноценным, мы «сжимаем» наименее подходящие. Представьте, что обучающие примеры — это точки в комнате и высота для наших целей не требуется. Если ее отбросить, все примеры спроецируются на пол. Произвести понижающее взвешивание — все равно что опустить в комнате потолок. Высота точки все еще засчитывается при вычислении расстояния до других точек, но уже меньше, чем ее горизонтальное положение. И, как и многое другое в машинном обучении, вес атрибутов можно найти путем градиентного спуска.

Может случиться, что потолок в комнате высокий, а точки данных лежат рядом с полом, как тонкий слой пыли на ковре. В этом случае нам повезло: проблема выглядит трехмерной, но в сущности она ближе к двухмерной. Мы не будем сокращать высоту, потому что это уже сделала природа. Такое «благословение неравномерности» данных в (гипер)пространстве часто спасает положение. У примеров могут быть тысячи атрибутов, но в реальности все они «живут» в пространстве с намного меньшим числом измерений. Именно поэтому метод ближайшего соседа бывает хорош, например, для распознавания написанных вручную цифр: каждый пиксель — это измерение, поэтому измерений много, но лишь мизерная доля всех возможных изображений — цифры, и все они живут вместе в уютном уголке гиперпространства. Форма низко­размерного пространства c данными бывает, однако, довольно своенравна. Например, если в комнате стоит мебель, пыль оседает не только на пол, но и на столы, стулья, покрывала и так далее. Если можно определить примерную форму слоя пыли, покрывающей комнату, тогда останется найти координаты каждой точки на нем. Как мы увидим в следующей главе, целая субдисциплина машинного обучения посвящена открытию форм этих слоев путем, так сказать, прощупывания гиперпространства во тьме.

Змеи на плоскости

Метод ближайшего соседа оставался самым широко используемым обучающимся алгоритмом аналогистов вплоть до середины 1990-х, когда его затмили более гламурные кузены из других «племен». Но тут, сметая все на своем пути, на смену ворвался новый алгоритм, основанный на принципах сходства. Можно сказать, что это был еще один «дивиденд от мира», плод окончания холодной войны. Метод опорных векторов был детищем советского специалиста по частотному подходу Владимира Вапника. Вапник большую часть своей карьеры работал в московском Институте проблем управления, но в 1990 году Советский Союз рухнул, и ученый уехал в США, где устроился на работу в легендарную Bell Labs. В России Вапник в основном довольствовался теоретической, бумажной работой, но атмосфера в Bell Labs была иной. Исследователи стремились к практическим результатам, и Вапник наконец решился превратить свои идеи в алгоритм. В течение нескольких лет он с коллегами по лаборатории разработал метод опорных векторов, и вскоре опорные векторы оказались повсюду и принялись ставить новые рекорды точности.

На первый взгляд метод опорных векторов во многом похож на взвешенный алгоритм k-ближайших соседей: граница между положительными и отрицательными классами определяется мерой схожести примеров и их весами. Тестовый пример принадлежит к положительному классу, если в среднем он выглядит более похожим на положительные примеры, чем на отрицательные. Среднее взвешивается, и метод опорных векторов помнит только ключевые примеры, необходимые для проведения границы. Если еще раз посмотреть на Позистан и Негативию без городов, не расположенных на границе, останется такая карта:

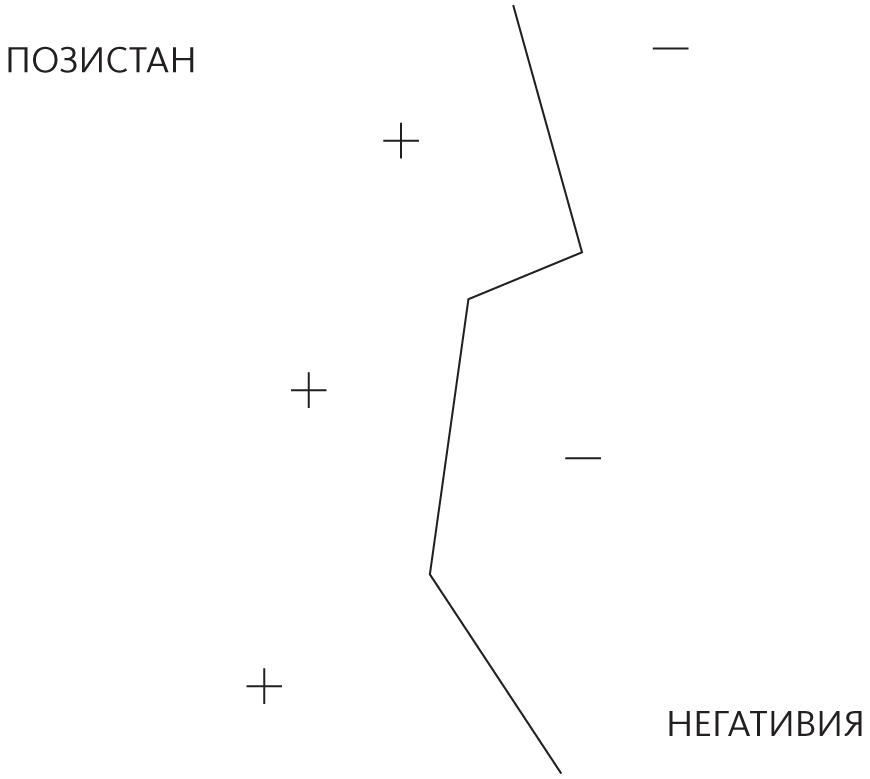
Примеры здесь называются опорными векторами, потому что это векторы, которые «поддерживают» границу: уберите один, и участок границы соскользнет в другое место. Также можно заметить, что граница представляет собой зубчатую линию с резкими углами, которые зависят от точного расположения примеров. У реальных понятий, как правило, границы более плавные, а это означает, что приближение, сделанное методом ближайшего соседа, вероятно, не идеально. Благодаря методу опорных векторов можно сделать границу гладкой, больше похожей на эту:

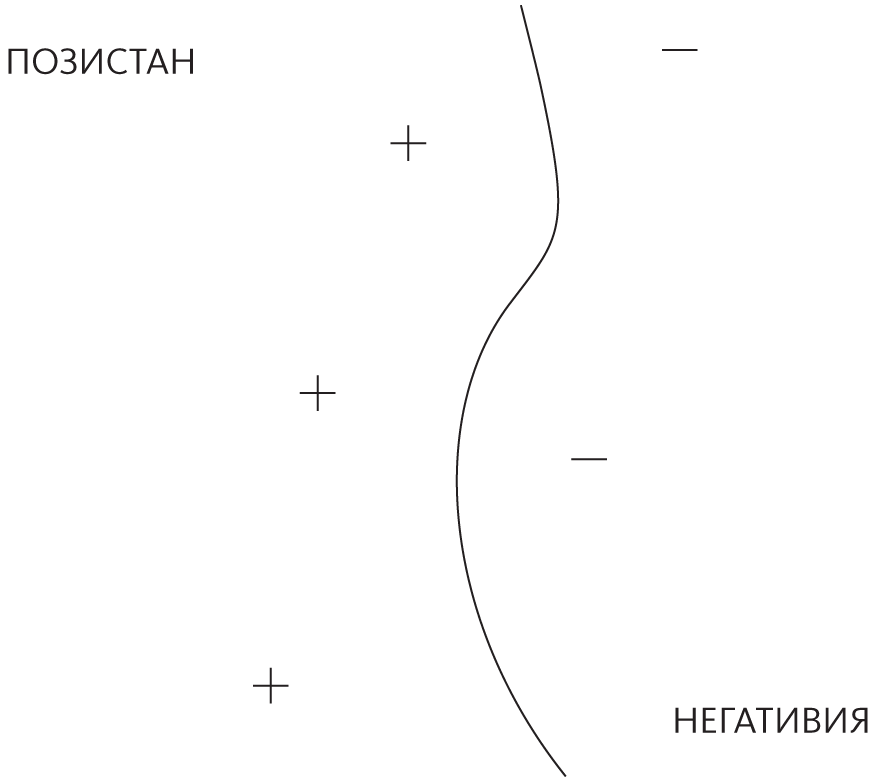
Чтобы обучить метод опорных векторов, нужно выбрать опорные векторы и их вес. Меру схожести, которая в мире опорных векторов называется ядром, обычно назначают априорно. Одним из важнейших открытий Вапника было то, что не все границы, отделяющие положительные тренировочные примеры от отрицательных, равноценны. Представьте, что Позистан воюет с Негативией и государства разделены нейтральной полосой с минными полями с обеих сторон. Ваша задача — исследовать эту ничейную землю, пройдя с одного ее конца к другому, и не взлететь на воздух. К счастью, у вас в руках карта c расположением мин. Вы, понятное дело, выберете не просто любую старую тропинку, а станете обходить мины как можно более широким кругом. Именно так поступает метод опорных векторов: мины для него — это примеры, а найденная тропа — выученная граница. Самое близкое место, где граница подходит к примеру, — ее зазор, и метод опорных векторов выбирает опорные векторы и веса так, чтобы зазор был максимальным. Например, сплошная прямая граница на этом рисунке лучше, чем пунктирная:

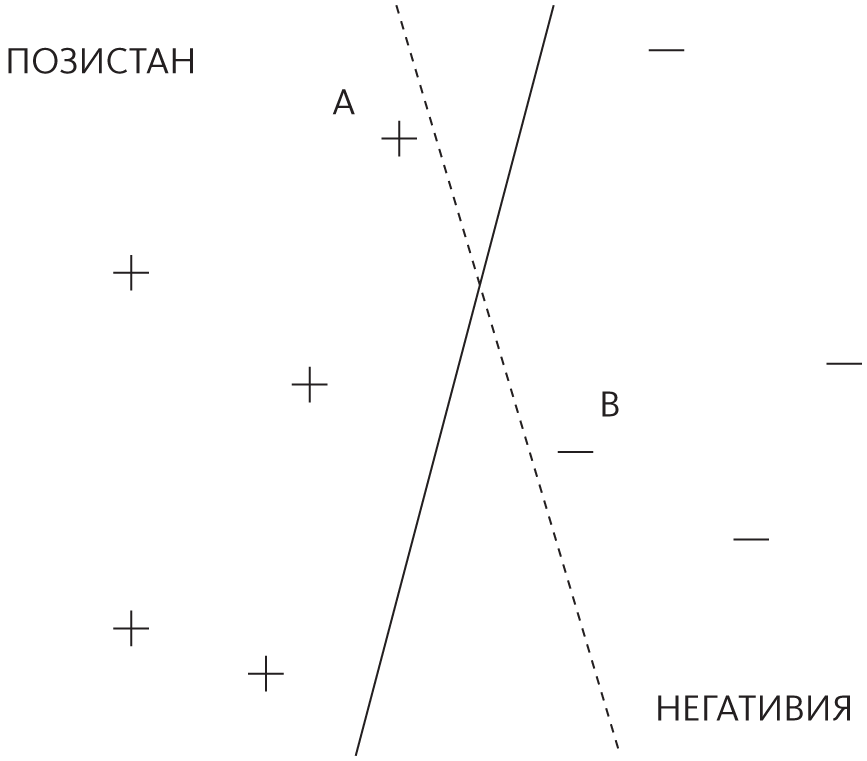
Пунктирная граница четко разделяет положительные и отрицательные примеры, но опасно близко подходит к минам A и B. Эти примеры — опорные векторы. Удалите один из них, и граница с максимальным зазором переместится в другое место. Конечно, граница может быть изогнутой, из-за чего зазор сложнее визуализировать, но можно представить себе, как по ничейной земле ползет змея и зазор — ее жировые отложения. Если без риска взорваться на кусочки может проползти очень толстая змея, значит, метод опорных векторов хорошо разделяет положительные и отрицательные примеры, и Вапник показал, что в этом случае можно быть уверенным, что метод не подвержен переобучению. Интуиция подсказывает, что у толстой змеи меньше способов проскользнуть мимо мин, чем у тощей, и точно так же, если зазор большой, у него меньше шансов переобучиться данным, нарисовав слишком замысловатую границу.

Вторая часть истории — это то, как метод опорных векторов находит самую толстую змею, способную проползти между положительными и отрицательными минами. Может показаться, что обучения весам для каждого тренировочного примера путем градиентного спуска будет достаточно. Надо просто найти веса, которые максимизируют зазор, и любой пример, который заканчивается нулевым весом, можно отбросить. К сожалению, в таком случае веса начали бы расти безгранично, потому что с точки зрения математики чем больше веса, тем больше зазор. Если вы находитесь в метре от мины и удвоите размер всего, включая вас самих, от мины вас станут отделять два метра, но это не уменьшит вероятности, что вы на нее наступите. Вместо этого придется максимизировать зазор под давлением того, что веса могут увеличиться лишь до какой-то фиксированной величины. Или аналогично можно минимизировать веса под давлением того, что все примеры имеют данный зазор, который может быть единицей — точное значение произвольно. Это то, что обычно делает метод опорных векторов.

Оптимизация при наличии ограничений — проблема максимизации или минимизации функции, в отношении которой действуют некие условия. Вселенная, например, максимизирует энтропию при условии сохранения постоянства энергии. Проблемы такого рода широко распространены в бизнесе и технологиях. Можно стремиться максимизировать число единиц продукции, которое производит фабрика, при условии доступного числа машинных инструментов, спецификаций продукции и так далее. С появлением метода опорных векторов оптимизация при наличии ограничений стала критически важной и в машинном обучении. Неограниченная оптимизация сравнима с тем, как добраться до вершины горы, и именно это делает градиентный спуск (в данном случае восхождение). Ограниченная оптимизация — все равно что зайти как можно выше, но при этом не сходить с дороги. Но если дорога будет доходить до самой вершины, ограниченные и неограниченные проблемы будут иметь одно и то же решение. Однако чаще дорога сначала петляет вверх по горе, а затем сворачивает вниз, так и не достигнув вершины. Вы понимаете, что достигли высочайшей точки дороги, и не можете зайти выше, не съехав с нее. Другими словами, путь к вершине находится под прямым углом к дороге. Если дорога и путь к вершине образуют острый или тупой угол, всегда можно забраться еще выше, продолжая ехать по доро­ге, даже если вы не подниметесь так быстро, как если бы пошли прямо к вершине. Поэтому для решения проблемы ограниченной оптимизации надо следовать не по градиенту, а по его части, параллельной поверхности ограничения — в данном случае дороги, — и остановиться, когда эта часть будет равна нулю.

В целом нам надо справиться со многими ограничениями сразу (в случае метода опорных векторов — по одному на каждый пример). Представьте, что вы хотите подобраться как можно ближе к Северному полюсу, но не можете выйти из комнаты. Каждая из четырех стен комнаты — это ограничение, поэтому для решения задачи надо идти по компасу, пока вы не упретесь в угол, где встречаются северо-восточная и северо-западная стена. Эти стены будут активными ограничениями, потому что они не дадут вам достичь оптимума, а именно Северного полюса. Если одна из стен вашей комнаты смотрит точно на север, она станет единственным активным ограничением; для решения надо направиться в ее центр. А если вы Санта-Клаус и живете прямо на Северном полюсе, все ограничения окажутся неактивными и можно будет сесть и поразмышлять над проблемой оптимального распределения игрушек. (Бродячим торговцам легче, чем Санте.) В методе опорных векторов активные ограничения — опорные векторы, поскольку их зазоры уже наименьшие из разрешенных. Перемещение границы нарушило бы одно или больше ограничений. Все другие примеры не имеют отношения к делу и их вес равен нулю.

В реальности методу опорных векторов обычно разрешается нарушать некоторые ограничения, то есть классифицировать некоторые примеры неправильно или менее чем на зазор, потому что в противном случае будет возникать переобучение. Если где-то в центре положительной области есть негативный пример, создающий шум, нам не надо, чтобы граница вилась внутри положительной зоны просто ради того, чтобы правильно классифицировать этот пример. Однако за каждый неправильно определенный пример начисляются штрафные баллы, и это стимулирует метод опорных векторов сводить их к минимуму. Так что данный метод как песчаные черви в «Дюне»: большие, мощные и способные пережить довольно много взрывов, но не слишком много.

В поисках применения своему алгоритму Вапник и его сотрудники вскоре вышли на распознавание написанных от руки цифр, в котором их коллеги-коннекционисты в Bell Labs были мировыми экспертами. Ко всеобщему удивлению, метод опорных векторов с ходу справился не хуже многослойного перцептрона, который тщательно, годами оттачивали для распознавания цифр. Это подготовило почву для долгой интенсивной конкуренции между методами. Метод опорных векторов можно рассматривать как обобщение перцептрона, использование специфической меры сходства (скалярного произведения векторов) даст гиперплоскостную границу между классами. Но у метода опорных векторов имеется большое преимущество по сравнению с многослойными перцептронами: у весов есть единичный оптимум, а не много локальных, и поэтому их намного легче надежно найти. Несмотря на это, опорные векторы не менее выразительны, чем многослойные перцептроны: опорные векторы фактически действуют как скрытый слой, а их взвешенное среднее — как выходной слой. Например, метод опорных векторов может легко представлять функцию исключающего ИЛИ, имея один опорный вектор для каждой из четырех возможных конфигураций. Но и коннекционисты не сдавались без боя. В 1995 году Ларри Джекел, глава отдела Bell Labs, в котором работал Вапник, поспорил с ним на хороший обед, что к 2000 году нейронные сети будут так же понятны, как метод опорных векторов. Он проиграл. В ответ Вапник поспорил, что к 2005 году никто не будет пользоваться нейронными сетями. И тоже проиграл. (Единственным, кто бесплатно пообедал, был Янн Лекун, их свидетель.) Более того, с появлением глубокого обучения коннекционисты снова взяли верх. При условии обучаемости, сети со многими слоями могут выражать многие функции компактнее, чем метод опорных векторов, у которого всегда только один слой, а это иногда имеет решающее значение.

Другим заметным ранним успехом метода опорных векторов была классификация текстов, которая оказалась большим благом для зарождающегося интернета. В то время самым современным классификатором был наивный байесовский алгоритм, но, когда каждое слово в языке — это измерение, даже он мог начать переобучаться. Для этого достаточно слова, которое по случайности в тренировочных данных встречается на всех спортивных страницах и ни на каких других: в этом случае у наивного Байеса появятся галлюцинации, что любая страница, содержащая это слово, посвящена спорту. А метод опорных векторов благодаря максимизации зазора может сопротивляться переобучению даже при очень большом числе измерений.

В целом чем больше опорных векторов выбирает метод, тем лучше он обобщает. Любой обучающий пример, который не представляет собой опорный вектор, будет правильно классифицирован, если появит­ся в тестовой выборке, потому что граница между положительными и отрицательными примерами по-прежнему будет на том же месте. Поэтому ожидаемая частота ошибок метода опорных векторов, как правило, равна доле примеров, являющихся опорными векторами. По мере роста числа измерений эта доля тоже будет расти, поэтому метод не застрахован от проклятия размерности, но он более устойчив к нему, чем большинство алгоритмов.

Кроме практических успехов, метод опорных векторов перевернул с ног на голову много воззрений, которые олицетворяли здравый смысл в машинном обучении. Например, опроверг утверждение, которое иногда путают с бритвой Оккама, что более простые модели точнее. Метод может иметь бесконечное число параметров и все равно не переобучаться при условии, что у него достаточно большой зазор.

Самое неожиданное свойство метода опорных векторов заключается в следующем: какие бы изогнутые границы он ни проводил, эти границы всегда будут прямыми линиями (или гиперплоскостями). В этом нет противоречия. Причина заключается в том, что прямые линии будут находиться в другом пространстве. Допустим, примеры живут на плос­кости (x, y), а граница между положительными и отрицательными областями — это парабола y = x². Ее невозможно представить в виде прямой линии, но, если мы добавим третью координату z [данные окажутся в пространстве (x, y, z)] и установим координату z каждого примера равной квадрату его координаты x, граница будет просто диагональной плоскостью, определенной y = z. В результате точки данных поднимутся в третье измерение, некоторые больше, чем другие, но ровно настолько, насколько нужно, и — вуаля! — в этом новом измерении положительные и отрицательные примеры можно будет разделить плоскостью. То, что метод делает с ядрами, опорными векторами и весами, можно рассматривать как картирование данных в более высокоразмерное пространство и нахождение в этом пространстве гиперплоскости с максимальным зазором. Для некоторых ядер полученное поле имеет бесконечное число измерений, но для метода опорных векторов это совершенно не важно. Может быть, гиперпространство — это и сумеречная зона, но метод опорных векторов знает, как находить в ней путь.

Вверх по лестнице

Две вещи схожи, если они в определенном отношении совпадают друг с другом. Если они в чем-то совпадают, вероятно, в чем-то они будут отличаться. В этом суть аналогии. Это указывает и на две главные подпроблемы рассуждения по аналогии: как понять, насколько похожи две вещи, и как решить, какие выводы можно сделать из этих сходств. Пока мы исследовали «маломощную» область аналогии — алгоритмы вроде ближайшего соседа и метод опорных векторов, — ответы на оба вопроса были очень простыми. Такие алгоритмы наиболее популярны, но глава об аналогическом обучении будет неполной, если мы хотя бы бегло не рассмотрим более мощные части спектра.

Самый главный вопрос во многих аналогических обучающихся алгоритмах — как измерять сходство. Это может быть просто евклидово расстояние между точками данных или, сложнее, целая программа с многочисленными слоями подпрограмм, которая в конце выдает значение сходства. Так или иначе функция сходства контролирует, как алгоритм машинного обучения обобщает из известных примеров в новые. Именно здесь мы вводим в обучающийся алгоритм наши знания о данной области: это ответ аналогизаторов на вопрос Юма. Аналогическое обучение можно применять ко всем видам объектов, а не только к векторам атрибутов, при условии, что есть какой-то способ измерить сходство между ними. Например, сходство между двумя молекулами можно определить по числу идентичных субструктур, которые они содержат. Метан и метанол схожи, потому что в них есть три связи углерода с водородом, а отличаются они только тем, что в метаноле один атом водорода замещен гидроксильной группой:

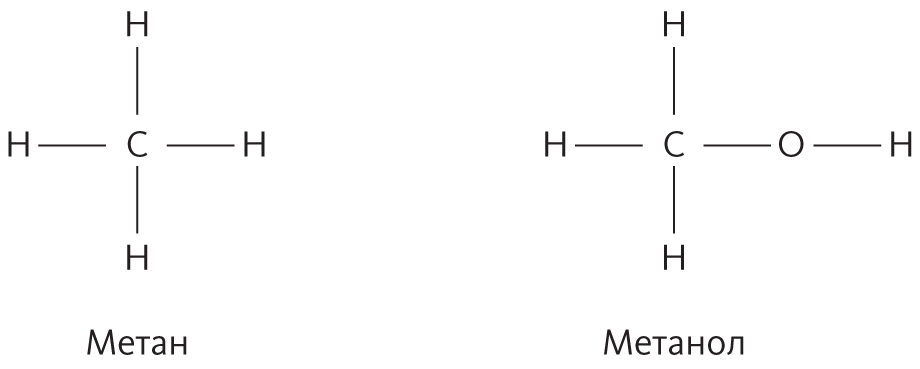
Однако это не означает, что схожи химические свойства веществ, ведь метан — это газ, а метанол — спирт. Вторая часть аналогического рассуждения — попытка разобраться, какие выводы можно сделать о новом объекте на основе найденных аналогов. Это бывает и очень просто, и очень сложно. В случае алгоритма ближайшего соседа и метода опорных векторов это просто предсказание класса нового объекта на основе классов ближайших соседей или опорных векторов. Но в случае рассуждения по прецедентам — еще одного типа аналогического обучения — результатом может стать сложная структура, сформированная из элементов найденных объектов. Представьте, что ваш принтер печатает абракадабру и вы звоните в службу поддержки Hewlett-Packard. Есть шанс, что они уже много раз встречались с аналогичной проблемой, поэтому будет правильно найти старые записи и сложить из них потенциальное решение. Мало просто найти жалобы, у которых много общих атрибутов с вашей: например, в зависимости от установленной операционной системы — Windows или Mac OS X — нужен будет очень разный набор настроек и системы, и принтера. Когда самые подходящие случаи найдены, требуемой последовательностью шагов, необходимых для решения вашей проблемы, может оказаться сочетание этапов из разных случаев плюс какие-то дополнительные, специфические элементы.

В настоящее время службы поддержки — это самое популярное применение рассуждения на основе прецедентов. Большинство из них все еще используют посредника-человека, но Eliza IPsoft уже сама общается с клиентом. Эта система дополнена интерактивным 3D-изображением женщины и на сегодняшний день уже решила более 20 миллионов проблем клиентов в основном престижных американских компаний. «Привет из Роботистана, самого дешевого нового направления аутсорсинга», как недавно писали в одном блоге по аутсорсингу. Поскольку аутсорсинг постоянно охватывает все новые профессии, вместе с ним совершенствуется и аналогическое обучение. Уже созданы первые роботы-адвокаты, которые отстаивают тот или иной вердикт на основе прецедентов. Одна из таких систем точно предсказала результаты более 90 процентов рассмотренных ею дел о нарушении производственной тайны. Может быть, в будущем на сессии киберсуда где-нибудь в облаке Amazon робот-адвокат будет оспаривать штраф за превышение скорости, который робот-полицейский выписал вашему беспилотному автомобилю, а вы тем временем станете нежиться на пляже. Тогда мечта Лейбница о сведении всех аргументов к вычислениям наконец сбудется.

Вероятно, труд композитора находится еще выше на лестнице умений. Дэвид Коуп, почетный профессор музыки в Калифорнийском университете в Санта-Круз, разработал алгоритм, который пишет новые музыкальные произведения в стиле известных композиторов путем отбора и рекомбинации коротких отрывков из их сочинений. На конференции, в которой я несколько лет назад участвовал, Коуп продемонстрировал три пьесы: одну на самом деле написанную Моцартом, другую — композитором, имитировавшим его, и третью — сгенерированную системой. Затем Коуп попросил аудиторию проголосовать. Вольфганг Амадей победил, но имитатор-человек уступил компьютеру. Поскольку это была конференция по искусственному интеллекту, публика осталась довольна. На других мероприятиях восторгов было куда меньше. Некоторые слушатели сердито обвиняли Коупа в том, что он уничтожает музыку. Если Коуп прав, то творчество — высшее из непостижимого — сводится к аналогии и рекомбинации. Попробуйте свои силы: найдите в Google «david cope mp3» и послушайте.

Однако самый изящный трюк аналогизаторов — это обучение на проб­лемах из разных областей. Люди практикуют это постоянно: менеджер может перейти, скажем, из медиакомпании в компанию, занимающу­юся потребительскими товарами, и не начнет с нуля, потому что многие управленческие навыки повторяются. На Уолл-стрит приглашают работать множество физиков, потому что физические и финансовые проблемы кажутся очень разными, но зачастую имеют схожую математическую структуру. Тем не менее все алгоритмы машинного обучения, которые мы до сих пор видели, пасуют, если мы натренируем их для предсказания, скажем, броунов­ского движения, а потом заставим делать прогнозы на фондовой бирже. Цены на бирже и скорости частиц, взвешенных в жидкости, — это разные переменные, поэтому обучающийся алгоритм даже не будет знать, с чего начать. Однако аналогизаторы могут сделать это, используя отображение структур — алгоритм, изобретенный психологом из Северо-Западного университета Дедре Джентнером. Отображение структур берет два описания, находит связное соответствие между некоторыми их элементами и соотношениями, а затем, основываясь на этом соответствии, переносит другие свойства одной структуры на другую. Например, если структуры — это Солнечная система и атом, можно отобразить планеты как электроны, а солнце — как ядро и заключить, подобно Бору, что электроны вращаются вокруг ядра. Истина, конечно, не такая прямолинейная, и уже сделанные аналогии часто приходится корректировать, но иметь возможность учиться на основе единичного примера, как этот, несомненно, ключевой атрибут универсального обучающегося алгоритма. Когда мы сталкиваемся с новым типом рака — а это происходит постоянно, потому что рак непрерывно мутирует, — модели, которые мы узнали из предыдущих случаев, оказываются неприменимы. У нас нет ни времени, чтобы собирать данные о новом типе опухоли, ни множества пациентов: может быть, пациент вообще уникальный, и он срочно нуждается в лекарстве. В таком случае надежду дает сравнение новой разновидности рака с уже известными: попытаться найти похожий случай и предположить, что сработают те же стратегии лечения.

Есть ли что-то, на что неспособна аналогия? Нет, считает Даглас Хофштадтер, когнитивный психолог и автор книги Gödel, Escher, Bach: An Eternal Golden Braid. Хофштадтер немного похож на доброго близнеца Гринча — похитителя Рождества и, вероятно, является самым знаменитым аналогизатором в мире. В книге Surfaces and Essences: Analogy as the Fuel and Fire of Thinking («Поверхности и сущности: аналогия в роли топлива и огня мышления») Хофштадтер и Эммануэль Сандер страстно доказывают, что все разумное поведение сводится к аналогии. Все, что мы узнаём или открываем, начиная со значения повседневных слов, например «мама» и «играть», до гениальных прозрений Альберта Эйнштейна и Эвариста Галуа, — это продукт аналогии. Когда малыш Тим видит, что какие-то женщины присматривают за другими детьми так же, как его собственная мама присматривает за ним, он обобщает понятие «мамочка» до мамы каждого человека, а не только его. Это, в свою очередь, трамплин к таким понятиям, как «мать-природа». «Самая счастливая мысль» Эйнштейна, из которой выросла общая теория относительности, была аналогией между гравитацией и ускорением: если вы едете в лифте, невозможно сказать, с какой из этих сил связан ваш вес, потому что результат одинаков. Мы плывем по широкому океану аналогий, манипулируем ими в своих целях, а они, не ведая того, манипулируют нами. В книгах аналогии встречаются на каждой странице (например, заголовки этого и предыдущего раздела). Gödel, Escher, Bach: An Eternal Golden Braid — расширенная аналогия между теоремой Гёделя, искусством Эшера и музыкой Баха. Если Верховный алгоритм — это не аналогия, он несомненно должен быть в чем-то схож с ней.

Взойди и сияй

В когнитивистике давно не утихают дебаты между символистами и аналогизаторами. Символисты показывают вещи, которые умеют моделировать они, но не умеют аналогизаторы. Затем аналогизаторы решают задачу, указывают на слабые места символистов, и цикл повторяется. Обучение на основе примеров, как его иногда называют, предположительно лучше подходит для моделирования запоминания отдельных эпизодов нашей жизни, а правила, предположительно, лучше выбрать для рассуждений с абстрактными концепциями, например «работа» и «любовь». Когда я был студентом, меня осенило: это ведь просто указывает на существование континуума, и надо уметь учиться на всем его протяжении. Правила — это, по сути, обобщенные частные случаи, где мы «забыли» некоторые атрибуты, потому что они не имеют значения. Частные же случаи — очень конкретные правила с условием для каждого атрибута. В жизни аналогичные эпизоды постепенно абстрагируются и образуют основанные на правилах структуры, например «есть в ресторане». Вы знаете, что пойти в ресторан — это и заказать что-нибудь из меню, и дать чаевые, и следуете этим «правилам поведения» каждый раз, когда едите вне дома. При этом вы, вероятно, и не вспомните, в каком заведении впервые все это осознали.

В своей диссертации я разработал алгоритм, объединяющий обучение на основе частных случаев и на основе правил. Правило не просто подходит к сущностям, которые удовлетворяют всем его условиям: оно подходит к любой сущности, которая похожа на него больше, чем на любое другое правило, и в этом смысле приближается к удовлетворению его условий. Например, человек с уровнем холестерина 220 мг/дл ближе, чем человек с 200 мг/дл, подходит к правилу «Если холестерин выше 240 мг/дл, есть риск сердечного приступа». RISE, как я назвал этот алгоритм, в начале обучения относится к каждому обучающему примеру как к правилу, а затем постепенно обобщает эти правила, впитывая ближайшие примеры. В результате обычно получается сочетание очень общих правил, которые в совокупности подходят к большинству примеров, плюс большое количество конкретных правил, которые подходят к исключениям, и так далее по «длинному хвосту» конкретных воспоминаний. RISE в то время предсказывал успешнее, чем лучшие обучающие алгоритмы, основанные на правилах и частных случаях. Мои эксперименты показали, что его сильной стороной было именно сочетание плюсов обоих подходов. Правила можно подобрать аналогически, и поэтому они перестают быть хрупкими. Частные случаи могут выбирать разные свойства в разных областях пространства и тем самым борются с проклятием размерности намного лучше метода ближайшего соседа, который везде выбирает одни и те же свойства.

RISE был шагом в сторону Верховного алгоритма, потому что соединял в себе символическое и аналогическое обучение. Однако это был лишь маленький шажок, потому что он не обладал полной силой этих парадигм и в нем по-прежнему не хватало трех оставшихся. Правила RISE нельзя было по-разному сложить в цепочку: они просто предсказывали класс примера на основе его атрибутов. Правила не могли рассказать о более чем одной сущности одновременно. Например, RISE не умел выражать правила вроде «Если у A грипп и B контактировал с A, то у B тоже может быть грипп». В аналогической части RISE лишь обобщал простой алгоритм ближайшего соседа. Он не может учиться в разных областях, используя отображение структур или какую-то схожую стратегию. Заканчивая работу над диссертацией, я не знал, как сложить в один алгоритм всю мощь пяти парадигм, и на время отложил проблему. Но, применяя машинное обучение к таким проблемам, как реклама из уст в уста, интеграция данных, программирование на примерах и персонализация сайтов, я постоянно замечал, что все парадигмы по отдельности дают лишь часть решения. Должен быть способ лучше.

Итак, проходя через территории пяти «племен», мы собирали их открытия, вели разговоры о границах и задумывались, как сложить вместе кусочки мозаики. Сейчас мы знаем неизмеримо больше, чем в начале пути, но чего-то по-прежнему не хватает. В центре мозаики зияет дыра, и поэтому собрать ее трудно. Проблема в том, что все алгоритмы машинного обучения, которые мы до сих пор видели, нуждаются в учителе, который покажет им правильный ответ. Они не могут научить­ся отличать опухолевую клетку от здоровой, если кто-то не повесит ярлыки «опухоль» и «здоровая клетка». А люди могут учиться без учителя, и делают это с самого первого дня своей жизни. Мы подошли к вратам Мордора, и долгий путь будет напрасным, если не обойти это препятствие. Но вокруг бастионов и стражников есть тропинка, и награда близка. Следуйте за мной…

Отправить