ГЛАВА 8

ОБУЧЕНИЕ БЕЗ УЧИТЕЛЯ

Если вы родитель, все тайны обучения разворачивались прямо на ваших глазах в первые три года жизни ребенка. Новорожденный не умеет говорить, ходить, узнавать предметы и даже не понимает, что то, на что он смотрит, будет существовать и когда он отвернется. Но проходит месяц за месяцем, и маленькими и большими шажками, путем проб, ошибок и больших когнитивных скачков ребенок разбирается, как устроен мир, как ведут себя люди, как с ними общаться. К третьему году плоды обучения сливаются в стабильное «я», в поток сознания, который не прекратится до самой смерти. Более старшие дети и взрослые способны «путешествовать во времени» — вспоминать прошлое, но лишь до этой границы. Если бы мы могли вернуться в младенчество и раннее детство и снова увидеть мир глазами маленького ребенка, многое, что озадачивает нас в механизмах обучения и даже самого бытия, внезапно стало бы очевидным. Но пока величайшая тайна Вселенной — это не ее зарождение или границы и не нити, из которых она соткана, а то, что происходит в мозге маленького ребенка: как из массы серого желе вырастает средоточие сознания.

Хотя наука о механизмах обучения детей все еще молода и исследования начались всего несколько десятилетий назад, ученые уже добились замечательных успехов. Младенцы не умеют заполнять анкеты и не соблюдают протоколов, однако удивительно много информации о том, что происходит у них в голове, можно получить благодаря видеозаписи и изучению их реакций во время эксперимента. Складывается связная картина: разум младенца — это не просто реализация заложенной генетической программы и не биологический прибор для фиксирования корреляций данных, получаемых из органов чувств. Разум ребенка сам активно синтезирует реальность, и со временем она меняется довольно радикально.

Очень удобно, что ученые-когнитивисты все чаще выражают теории детского обучения в форме алгоритмов. Это вдохновляет многих исследователей машинного обучения — ведь все, что нужно, уже есть там, в мозге ребенка, и надо только каким-то образом ухватить суть и записать ее в компьютерном коде. Некоторые ученые даже утверждают, что для создания разумных машин нужно сконструировать робота-ребенка и позволить ему ощутить мир так, как это делают обычные дети. Мы, исследователи, станем ему родителями (может быть, это будет краудсорсинг, и термин «глобальная деревня» приобретет совершенно новое значение). Маленький Робби — давайте назовем его в честь пухлого, но высокого робота из «Запретной планеты» — единственный робот-ребенок, которого нам надо построить. Как только он обучится всему, что человек знает в три года, проблема искусственного интеллекта будет решена. После этого можно скопировать содержимое его мозга в столько роботов, во сколько захотим, и они будут развиваться дальше: самое сложное уже сделано.

Вопрос, конечно, в том, какие алгоритмы должны работать в мозге Робби в момент рождения. Ученые, находящиеся под влиянием детской психологии, косо смотрят на нейронные сети, потому что работа нейронов на микроскопическом уровне кажется бесконечно далекой от сложности даже простейших действий ребенка: потянуться к предмету, схватить его и рассмотреть широко распахнутыми, полными любопытства глазами. Чтобы за деревьями увидеть планету, обучение ребенка придется моделировать на более высоком уровне абстракции. Самое удивительное, наверное, то, что дети учатся в основном самостоятельно, без надзора, хотя, несомненно, получают огромную помощь от своих родителей. Ни один из алгоритмов, которые мы до сих пор видели, на это не способен, но вскоре мы познакомимся с несколькими вариантами и на шаг приблизимся к Верховному алгоритму.

Как свести рыбака с рыбаком

Мы нажимаем кнопку «Включить», Робби открывает глаза-видео­камеры в первый раз, и его сразу заливает «цветущий и жужжащий беспорядок» мира, как сказал Уильям Джеймс. Новые изображения возникают десятками в секунду, и одна из первоочередных задач — научиться организовывать их в более крупные элементы: реальный мир состоит не из случайных пикселей, которые каждое мгновение меняются, как им вздумается, а из стабильных во времени объектов. Если мама отошла подальше, вместо нее не появится «уменьшенная мама». Если на стол поставить тарелку, в столе не появится белая дырка. Младенец не отреагирует, если плюшевый мишка скроется за ширмой и вместо него появится самолет, а годовалый ребенок удивится: он каким-то образом уже сообразил, что мишки отличаются от самолетов и не могут просто так превращаться друг в друга. Вскоре после этого он разберется, что некоторые предметы похожи друг на друга, и начнет формировать категории. Если девятимесячному малышу дать гору игрушечных лошадок и карандашей, он и не подумает их разделить, а в полтора года уже догадается.

Организация мира в предметы и категории совершенно естественна для взрослого, но не для младенца, и в еще меньшей степени для робота Робби. Можно, конечно, одарить его зрительной корой в виде многослойного перцептрона и показать подписанные примеры всех предметов и категорий в мире — вот мама рядом, а вот мама далеко, — но так мы никогда не закончим. На самом деле нам нужен алгоритм, который будет спонтанно группировать схожие объекты и разные изображения одного и того же объекта. Это проблема кластеризации, одна из наиболее интенсивно изучаемых тем в науке о машинном обучении.

Кластер — это набор схожих сущностей или как минимум набор сущностей, которые похожи друг на друга больше, чем на элементы других кластеров. Делить все на кластеры — в природе человека, и часто это первый шаг на пути к знанию. Даже глядя в ночное небо, мы невольно видим скопления звезд, а потом придумываем красивые названия формам, которые они напоминают. Наблюдение, что определенные группы веществ имеют очень схожие химические свойства, стало первым шагом к открытию периодической системы элементов: каждая группа в ней заняла свой столбец. Все, что мы воспринимаем — от лиц друзей до звуков речи, — это кластеры. Без них мы бы потерялись. Дети не научатся говорить, пока не приобретут навык определять характерные звуки, из которых состоит речь. Это происходит в первые годы жизни, и все слова, которые они потом узнают, не значат ничего без кластеров реальных вещей, к которым эти слова относятся. Сталкиваясь с большими данными — очень большим количеством объектов, — мы вначале группируем их в удобное число кластеров. Рынок в целом — слишком общий, отдельные клиенты — слишком мелкие, поэтому маркетологи делят его на сегменты, как они называют кластеры. Даже объекты как таковые, по сути, кластеры наблюдений за ними, начиная с маминого лица под разными углами освещения и заканчивая различными звуковыми волнами, которые ребенок слышит как слово «мама». Думать без объектов невозможно, и, наверное, именно поэтому квантовая механика такая неинтуитивная наука: субатомный мир хочется нарисовать в воображении в виде сталкивающихся частиц или интерферирующих волн, но на самом деле это ни то ни другое.

Кластер можно представить по его элементу-прототипу: образу мамы, который сразу приходит на ум, типичной кошки, спортивного автомобиля, загородного дома и тропического пляжа. Для маркетолога Пеория в штате Иллинойс это средний американский городок. Самый обычный гражданин США — это Боб Бернс, пятидесятитрехлетний завхоз из Уиндема в штате Коннектикут, по крайней мере, если верить книге Кевина О’Кифа The Average American. По всем числовым атрибутам — например, росту, весу, объему талии и обуви, длине волос и так далее — можно легко найти среднего члена кластера: его рост — это средний рост всех остальных, вес — средний вес и так далее. Для описательных атрибутов, например пола, цвета волос, почтового индекса и любимого вида спорта, «средним» значением будет просто самое распространенное. Средние члены кластеров, описанные таким набором атрибутов, могут существовать или не существовать в реальности, но это в любом случае удачные точки для ориентации: когда планируешь маркетинг нового продукта, удобнее представить себе Пеорию как место введения его на рынок и Боба Бернса как целевого клиента, а не оперировать абстрактными сущностями вроде «рынка» или «клиента».

Такие усредненные объекты, конечно, полезны, но можно поступить еще лучше: вообще весь смысл больших данных и машинного обучения как раз в том, чтобы избежать грубых рассуждений. Кластеры могут быть очень специализированными группами людей или даже различными аспектами жизни одного и того же человека: Элис, покупающая книги для работы, для отдыха или в подарок на Рождество, Элис в хорошем настроении и грустящая Элис. Amazon заинтересована в том, чтобы отделять книги, которые Элис покупает себе, от тех, которые она покупает для своего молодого человека, потому что тогда можно будет дать ей в нужное время подходящую рекомендацию. К сожалению, покупки не сопровождаются ярлыками «подарок для себя» и «для Боба», поэтому Amazon приходится самой разбираться, как их группировать.

Представьте, что объекты в мире Робби делятся на пять кластеров (люди, мебель, игрушки, еда и животные), но неизвестно, какие вещи к каким класте­рам относятся. С проблемой этого типа Робби столкнется, как только мы его включим. Простой вариант сортировки объектов по кластерам — взять пять произвольных предметов, сделать их прототипами кластеров, а затем сравнить новые сущности с каждым прототипом, относя их к кластеру самого схожего. (Как и в аналогическом обучении, здесь важно выбрать меру сходства. Если атрибуты числовые, это может быть просто евклидово расстояние, но это далеко не единственный вариант.)

Теперь прототипы надо обновить. Подразумевается, что прототип кластера должен быть средним его членов: когда кластеры состояли из одного члена, все так и было, но теперь мы добавили к ним новые элементы, и ситуация изменилась. Поэтому мы вычислим средние свойства членов для каждого кластера и сделаем полученный результат новым прототипом. Теперь нужно снова обновить принадлежность объектов кластерам: поскольку прототипы изменились, мог измениться и прототип, наиболее близкий данному объекту. Давайте представим, что прототип одной категории — это мишка, а другой — банан. Если взять крекер в виде животного, при первом подходе он может попасть в группу с медведем, а при втором — с бананом. Изначально крекер выглядел как игрушка, но теперь он будет отнесен к еде. Если пере­местить крекер в одну группу с бананом, прототип для этой группы тоже может измениться: это уже будет не банан, а печенье. Этот полезный цикл, который относит объекты ко все более и более подходящим кластерам, станет продолжаться, пока кластеры сущностей (а с ними и прототипы кластеров) не прекратят меняться.

Такой алгоритм называется метод k-средних, и появился он еще в 50-е годы ХХ века. Он простой, красивый, при этом довольно популярный, но имеет ряд недостатков, одни из которых устранить легче, а другие — сложнее. Во-первых, количество кластеров надо зафиксировать заранее, а в реальном мире Робби постоянно натыкается на новые виды предметов. Один вариант решения — позволить открывать новый кластер, если объект слишком сильно отличается от имеющихся. Другой — разрешить кластерам делиться и сливаться в процессе работы. Так или иначе, вероятно, будет целесообразно включить в алгоритм приоритеты для меньшего количества кластеров, чтобы избежать ситуации, когда у каждого предмета будет собственный кластер (идеальное решение, если кластеры должны содержать схожие предметы, но смысл явно не в этом).

Более серьезная проблема заключается в том, что метод k-средних работает, только когда кластеры легко различимы: они, как пузыри в гипер­пространстве, плавают далеко друг от друга, и у всех схожий объем и схожее количество членов. Если какое-то условие не выполнено, начинаются неприятности: вытянутые кластеры делятся надвое, маленькие поглощаются более крупными соседями и так далее. К счастью, можно поступить лучше.

Допустим, мы пришли к выводу, что разрешить Робби слоняться по реальному миру — слишком медленный и громоздкий способ обучения, и вместо этого посадили его смотреть сгенерированные компьютером изображения, как будущего летчика в авиационном тренажере. Мы знаем, из каких класте­ров взяты картинки, но не скажем об этом Робби, а будем создавать их, случайно выбирая кластер (скажем, «игрушки»), а потом синтезируя пример этого кластера (маленький пухлый бурый плюшевый медведь с большими черными глазами, круг­лыми ушами и галстуком-бабочкой). Кроме того, мы будем произвольно выбирать свойства примера: размер мишки — в среднем 25 сантиметров, мех с вероятностью 80 процентов бурый, иначе — белый и так далее. После того как Робби увидит очень много сгенерированных таким образом картинок, он должен научиться делить их на кластеры «люди», «мебель», «игрушки» и так далее, потому что люди, например, больше похожи на людей, а не на мебель. Возникает интересный вопрос: какой алгоритм кластеризации лучше с точки зрения Робби? Ответ будет неожиданным: наивный байесовский алгоритм — первый алгоритм для обучения с учителем, с которым мы познакомились. Разница в том, что теперь Робби не знает классов и ему придется их угадать!

Очевидно: если бы Робби их знал, все пошло бы отлично — как в наив­ном байесовском алгоритме, каждый кластер определялся бы своей вероятностью (17 процентов сгенерированных объектов — игрушки) и распределением вероятности каждого атрибута среди членов кластера (например, 80 процентов игрушек коричневые). Робби мог бы оценивать вероятности путем простого подсчета числа игрушек в имеющихся данных, количества коричневых игрушек и так далее, но для этого надо знать, какие предметы — игрушки. Эта проблема может показаться крепким орешком, но, оказывается, мы уже знаем, как ее решить. Если бы в распоряжении Робби имелся наивный байесовский классификатор и ему необходимо было определить класс нового предмета, нужно было бы только применить классификатор и вычислить вероятность класса при данных атрибутах объекта. Маленький, пухлый, коричневый, похож на медведя, с большими глазами и галстуком-бабочкой? Вероятно, игрушка, но, возможно, животное.

Итак, Робби сталкивается с проблемой «курица или яйцо»: зная классы предметов, он мог бы получить модели классов путем подсчета, а если бы знал модели, мог бы сделать заключение о классах объектов. Если вы думаете, что опять застряли, это далеко не так: чтобы стартовать, надо просто начать угадывать классы для каждого предмета каким угодно способом, даже произвольно. На основе этих классов и данных можно получить модели классов, на основе этих моделей — вновь сделать вывод о классах и так далее. На первый взгляд это кажется безумием: придется бесконечно кружиться между выводами о классах на основе моделей и моделей на основе их классов, и даже если это закончится, нет причин полагать, что кластеры получатся осмысленные. Но в 1977 году трое статистиков из Гарварда — Артур Демпстер, Нэн Лэрд и Дональд Рубин — показали, что сумасшедший план работает: после каждого прохождения по этой петле модель кластера улучшается, а после достижения моделью локального максимума похожести повторения заканчиваются. Они назвали эту схему EM-алгоритмом, где E — ожидания (expectation, заключение об ожидаемых вероятностях), а M — максимизация (maximization, оценка параметров максимальной схожести). Еще они показали, что многие предыдущие алгоритмы были частными случаями EM. Например, чтобы получить скрытые модели Маркова, мы чередуем выводы о скрытых состояниях с оценкой вероятностей перехода и наблюдения на их основе. Когда мы хотим получить статистическую модель, но нам не хватает какой-то ключевой информации (например, классов примеров), всегда можно использовать EM-алгоритм, что делает его одним из самых популярных инструментов в области машинного обучения.

Вы, возможно, заметили определенное сходство между методом k-средних и EM-алгоритмом, поскольку оба чередуют отнесение сущностей к кластерам и обновление описаний кластеров. Это не случайность: метод k-средних сам по себе — частный случай EM-алгоритма, который получается, если у всех атрибутов «узкое» нормальное распределение, то есть нормальное распределение с очень маленькой дисперсией. Если кластеры часто пере­крываются, объект может относиться, скажем, к кластеру A с вероят­ностью 0,7 и к кластеру B с вероятностью 0,3, и нельзя просто отнести его к кластеру A без потери информации. EM-алгоритм учитывает это путем частичного приписывания объекта к двум кластерам и соответствующего обновления описаний этих кластеров, однако, если распределения очень сконцентрированы, вероятность, что сущность принадлежит к ближайшему кластеру, всегда будет приблизительно равна единице, и нужно только распределить объекты по кластерам и усреднить их в каждом кластере, чтобы вычислить среднее — то есть получится алгоритм k-среднего.

До сих пор мы рассматривали получение всего одного уровня кластеров, но мир, конечно, намного богаче, и одни кластеры в нем вложены в другие вплоть до конкретных предметов: живое делится на растения и животных, животные — на млекопитающих, птиц, рыб и так далее до домашнего любимца — пса Фидо. Но проблем это не создает: получив набор кластеров, к ним можно относиться как к объектам и, в свою очередь, объединять их в кластеры все более высокого уровня, вплоть до кластера всех объектов. Или же можно начать с грубой кластеризации, а затем все больше дробить кластеры на подкластеры: игрушки Робби делятся на мягкие игрушки, конструкторы и так далее. Мягкие игрушки — на плюшевых медведей, котят и так далее. Дети, видимо, начинают изучение мира где-то посередине, а потом идут и вверх, и вниз. Например, понятие «собака» они усваивают до того, как узнают о «животных» и «гончих». Для Робби это может стать хорошей стратегией.

Открытие формы данных

Независимо от того, поступают ли данные в мозг Робби из его органов чувств или в виде потока миллионов кликов клиентов Amazon, сгруппировать множество в меньшее число кластеров — лишь половина дела. Второй этап — сократить описание объектов. Первый образ мамы, который видит Робби, будет состоять, может быть, из миллиона пикселей, каждый своего цвета, однако человеку вряд ли нужен миллион переменных, чтобы описать лицо. Аналогично каждый товар, на который вы кликнули на сайте Amazon, дает частицу информации о вас, но на самом деле Amazon интересны не ваши клики, а ваши вкусы. Вкусы довольно стабильны и в какой-то мере подразумеваются в кликах, количество которых растет безгранично во время пользования сайтом и должно понемногу складываться в картину предпочтений точно так же, как пиксели складываются в картинку лица. Вопрос в том, как реализовать это сложение.

У человека есть примерно 50 лицевых мышц, поэтому 50 чисел должно с лихвой хватить для описания всех возможных выражений лица. Форма глаз, носа, рта и так далее — всего того, что помогает отличить одного человека от другого, — тоже не должна занимать больше нескольких десятков чисел. В конце концов, художникам в полиции достаточно всего десяти вариантов каждой черты лица, чтобы составить фоторобот, позволяющий опознать подозреваемого. Можно добавить еще несколько чисел для описания осве­щения и наклона, но на этом все. Поэтому, если вы дадите мне примерно сотню чисел, этого должно хватить для воссоздания лица, и наоборот: мозг Робби должен быть способен взять картинку лица и быстро свести ее ко все той же сотне по-настоящему важных чисел.

Специалисты по машинному обучению называют этот процесс понижением размерности, потому что он уменьшает множество видимых измерений (пикселей) до нескольких подразумеваемых (выражение и черты лица). Понижение размерности важно для того, чтобы справиться с большим объемом данных, например данными, поступающими каждую секунду из органов чувств. Может быть, действительно лучше один раз увидеть, чем сто раз услышать, но обрабатывать и запоминать изображения в миллион раз сложнее, чем слова. Тем не менее зрительная кора головного мозга каким-то образом довольно хорошо справляется с уменьшением такого объема информации до приемлемого, достаточного, чтобы ориентироваться в мире, узнавать людей и предметы и помнить увиденное. Это великое чудо познания настолько естественно для нас, что мы его даже не замечаем.

Наводя порядок в своей библиотеке, вы тоже выполняете своего рода понижение размерности от обширного пространства тем до одномерной полки. Некоторые тесно связанные книги неизбежно окажутся далеко друг от друга, но все равно можно расставить их так, чтобы такие случаи были редкими. Алгоритм понижения размерности делает именно это.

Представьте, что я дал вам координаты GPS всех магазинов в Пало-Альто в Калифорнии и вы нанесли их на листок бумаги:

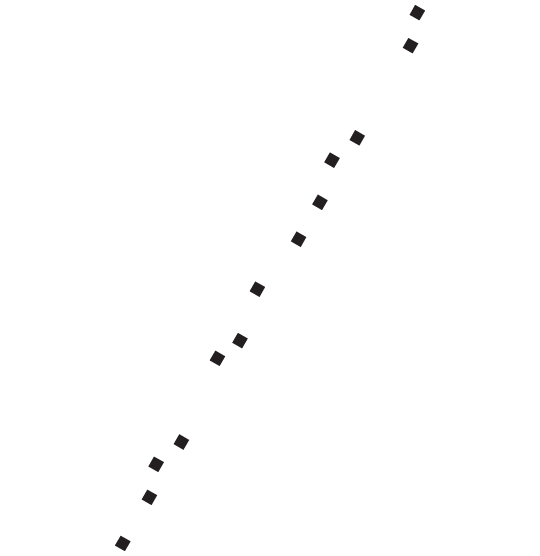
Наверное, взглянув на эту схему, вы сразу поймете, что главная улица городка ведет с юго-запада на северо-восток. Хотя вы не рисовали саму улицу, интуиция подсказывает, где она проходит, потому что все точки лежат на прямой линии (или рядом с ней — магазины могут быть по разные стороны улицы). Догадка верна: эта улица — Юниверсити-авеню, и, если вы окажетесь в Пало-Альто и захотите перекусить и сделать покупки, туда и надо идти. Еще лучше, что, когда магазины сконцентрированы на одной улице, для описания их расположения нужно уже не два числа, а всего одно — номер дома, а для большей точности — расстояние от магазина до пригородной железнодорожной станции в юго-западном углу, откуда начинается Юниверсити-авеню.

Если нанести на карту еще больше магазинов, вы, вероятно, заметите, что часть из них находится на перекрестках, чуть в стороне от Юниверсити-авеню, а некоторые — вообще в других местах:

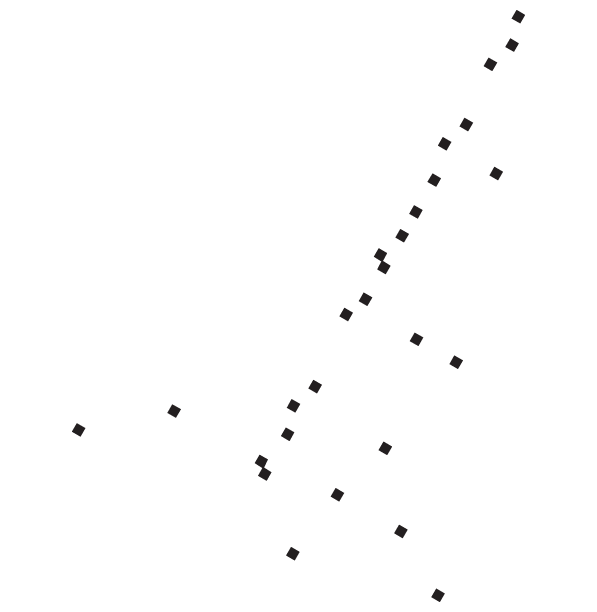
Тем не менее большинство магазинов все равно расположены довольно близко к центральной улице, и, если разрешено использовать для описания положения магазина только одно число, расстояние от вокзала вдоль этой улицы будет довольно удачным вариантом: пройдя этот отрезок и оглядевшись, вы с достаточной вероятностью найдете нужный магазин. Итак, вы только что понизили размерность «расположения магазинов в Пало-Альто» с двух измерений до одного.

У Робби, однако, нет преимуществ, которые дает человеку сильно развитая зрительная система, поэтому, если вы попросите его забрать белье из химчистки Elite Cleaners и учтете на его карте только одну координату, ему нужен будет алгоритм, чтобы «открыть» Юниверсити-авеню на основе GPS-координат магазинов. Ключ к решению проблемы — заметить, что, если поставить начало координат плоскости x, y в усредненное расположение магазинов и медленно поворачивать оси, магазины окажутся ближе всего к оси x при повороте примерно на 60 градусов, то есть когда ось совпадает с Юниверсити-авеню:

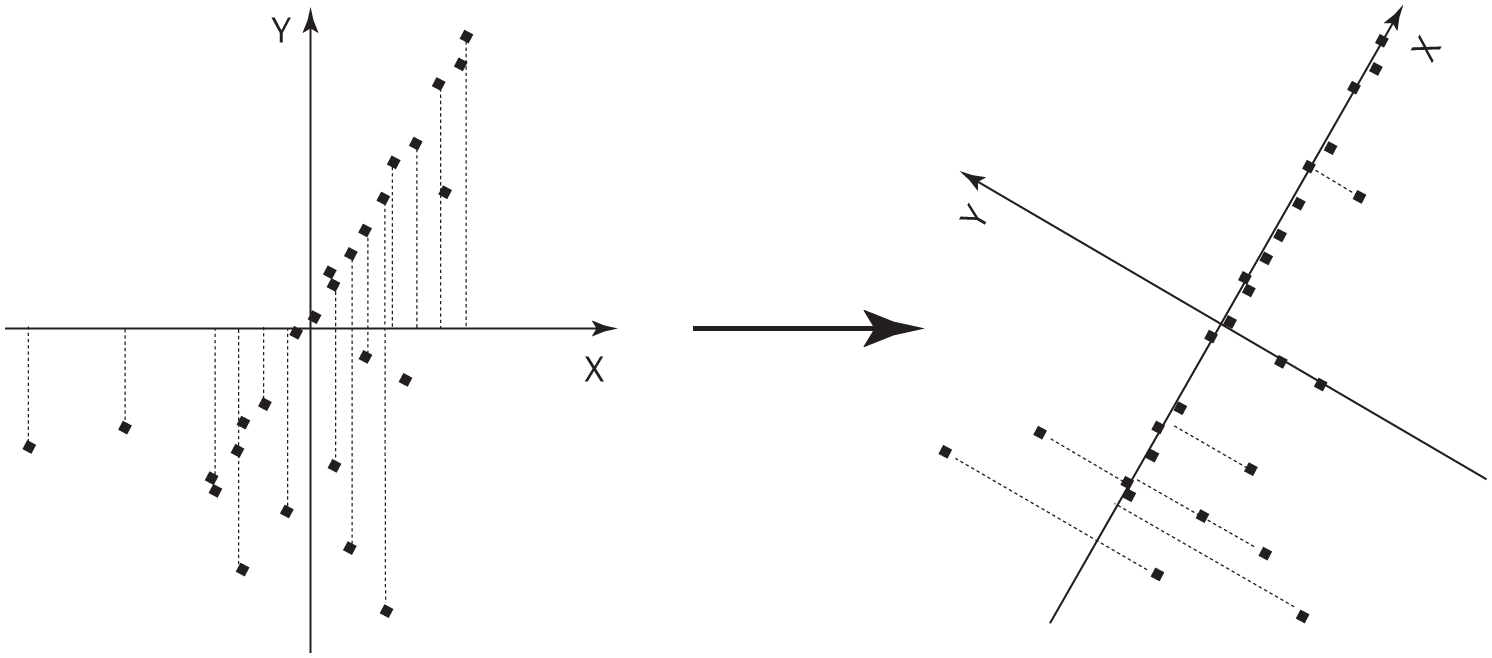
Это направление — так называемая первая главная компонента данных — будет направлением, вдоль которого разброс данных наибольший. (Обратите внимание: если спроецировать магазины на ось x, на правом рисунке они будут находиться дальше друг от друга, чем на левом.) Обнаружив первую главную компоненту, можно поискать вторую, которой в данном случае станет направление наибольшей дисперсии под прямым углом к Юниверсити-авеню. На карте остается только одно возможное направление (направление перекрестков). Но если бы Пало-Альто находился на склоне холма, одна или две главные компоненты частично были бы расположены непосредственно на холме, а третья — последняя — оказалась бы направлена в воздух. Ту же идею можно применить к тысячам и миллионам измерений данных, как в случае изображений лиц: нужно последовательно искать направления наибольшей дисперсии, пока оставшаяся вариабельность не окажется наименьшей. Например, после поворота осей на рисунке выше координата y большинства магазинов будет равна нулю, поэтому среднее y окажется очень маленьким, и, если его вообще проигнорировать, потеря информации получится незначительной. А если мы все же решим сохранить y, то z (направленная вверх) наверняка будет несущественна. Как оказалось, линейная алгебра позволяет провести процесс поиска главных компонент всего за один цикл, но еще лучше то, что даже в данных с очень большим количеством измерений значительную часть дисперсии зачастую дают всего несколько измерений. Если это не так, все равно визуальный поиск двух-трех важнейших измерений часто оказывается очень успешным, потому что наша зрительная система дает удивительные возможности восприятия.

Метод главных компонент (Principal Component Analysis, PCA), как называют этот процесс, — один из важнейших инструментов в арсенале ученого. Можно сказать, что для обучения без учителя это то же самое, что линейная регрессия для контролируемого множества. Знаменитая «клюшко­образная» кривая глобального потепления, например, была получена в результате нахождения главной компоненты различных рядов данных, связанных с температурой (годичные кольца деревьев, ледяные керны и так далее), и допущения, что это запись температуры как таковой. Биологи используют метод главных компонент, чтобы свести уровни экспрессии тысяч различных генов в несколько путей. Психологи обнаружили, что личность можно выразить пятью факторами — это экстраверсия, добро­желательность, добросовестность, нейротизм и открытость опыту, — которые оценивают по твитам и постам в блогах. (У шимпанзе, предположительно, есть еще одно измерение — реактивность, — но их с помощью Twitter не оценишь.) Применение метода главных компонент к голосам на выборах в Конгресс и данным избирателей показывает, что, вопреки расхожему мнению, политика в основном не сводится к противостоянию либералов и консерваторов. Люди отличаются в двух основных измерениях — экономических и социаль­ных вопросах, — и, если спроецировать их на одну ось, либертарианцы смешаются с популистами, хотя их позиции полярно противоположны, и возникнет иллюзия, что в центре много умеренных. Попытка апеллировать к ним вряд ли окажется выигрышной стратегией. С другой стороны, если либералы и либертарианцы преодолеют взаимную неприязнь, они могут стать союзниками в социальных вопросах, где и те и другие выступают за свободу личности.

Когда Робби подрастет, он сможет применять один из вариантов метода главных компонент для решения проблемы «эффекта вечеринки», то есть чтобы выделить из шума толпы отдельные голоса. Схожий метод может помочь ему научиться читать. Если каждое слово — измерение, тогда текст — точка в пространстве слов, и главные направления этого пространства окажутся элементами значения. Например, «президент Обама» и «Белый дом» в пространстве слов далеко отстоят друг от друга, но в пространстве значений близки, потому что обычно появляются в схожих контекстах. Хотите верьте, хотите нет, но такой тип анализа — все, что требуется и компьютерам, и людям для оценки сочинений на экзаменах SAT (стандартизованный тест для приема в высшие учебные заведения США). В Netflix используется похожая идея. Вместо того чтобы рекомендовать фильмы, которые понравились пользователям со схожими вкусами, система проецирует и пользователей, и фильмы в «пространство вкуса» с низкой размерностью и рекомендует картины, расположенные в этом пространстве рядом с вами. Это помогает найти фильмы, которые вы никогда не видели, но обязательно полюбите.

Тем не менее главные компоненты набора данных о лице вас, скорее всего, разочаруют. Вопреки ожиданиям, это будут, например, не черты лица и выражения, а скорее размытые до неузнаваемости лица призраков. Дело в том, что метод главных компонент — линейный алгоритм, поэтому главными компонентами могут быть только взвешенные пиксель за пикселем средние реальных лиц (их еще называют «собственные лица», потому что они собственные векторы центрированной ковариационной матрицы этих данных, но я отхожу от темы). Чтобы по-настоящему понять не только лица, но и большинство форм в мире, нам понадобится кое-что еще, а именно нелинейное понижение размерности.

Представьте, что вместо карты Пало-Альто у нас есть GPS-координаты важнейших городов всей Области залива Сан-Франциско:

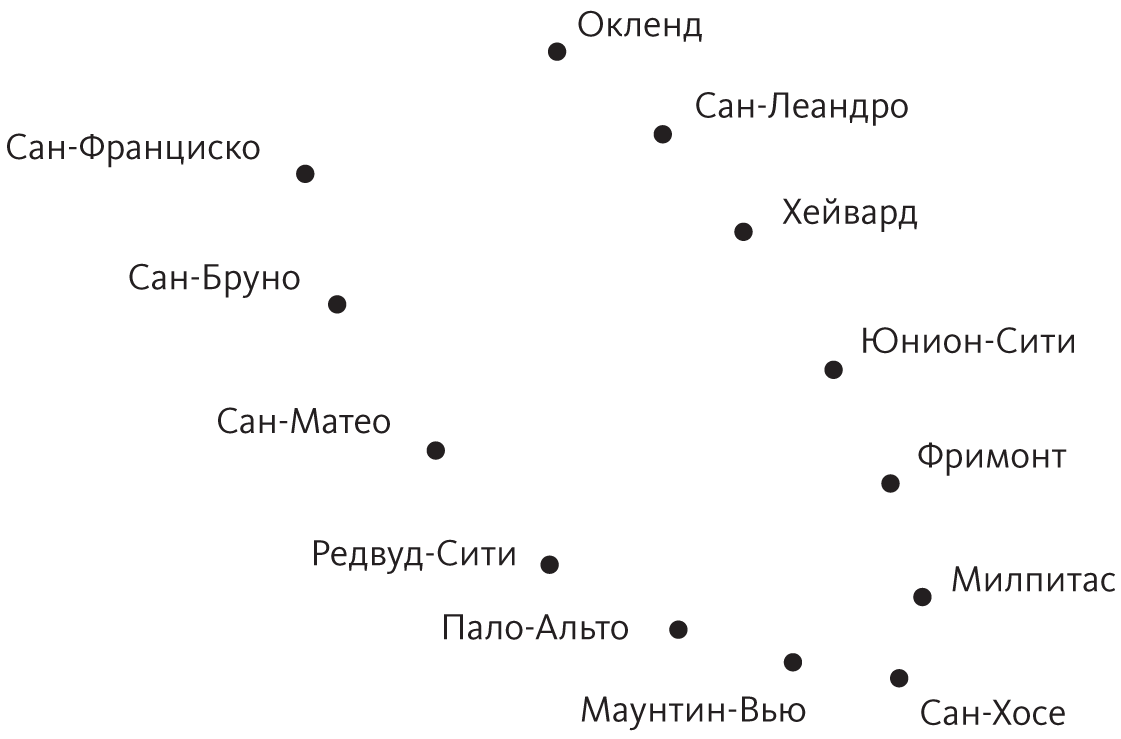
Глядя на эту схему, можно, вероятно, сделать предположение, что города расположены на берегу залива и, если провести через них линию, положение каждого города можно определить всего одним числом: как далеко он находится от Сан-Франциско по этой линии. Но метод главных компонент такую кривую найти не может: он нарисует прямую линию через центр залива, где городов вообще нет, а это только затуманит, а не прояснит форму данных.

Теперь представьте на секунду, что мы собираемся создать Область залива с нуля. Бюджет позволяет построить единую дорогу, чтобы соеди­нить все города, и нам решать, как она будет проложена. Естественно, мы проложим дорогу, ведущую из Сан-Франциско в Сан-Бруно, оттуда в Сан-Матео и так далее, вплоть до Окленда. Такая дорога будет довольно хорошим одномерным представлением Области залива, и ее можно найти простым алгоритмом: «построй дорогу между каждой парой близлежащих городов». Конечно, у нас получится целая сеть дорог, а не одна, проходящая рядом с каждым городом, но можно получить и одну дорогу, если сделать ее наилучшим приближением сети, в том смысле, что расстояния между городами по этой дороге будут как можно ближе расстоянию вдоль сети.

Именно это делает Isomap — один из самых популярных алгоритмов нелинейного понижения размерности. Он соединяет каждую точку данных в высокоразмерном пространстве (пусть это будет лицо) со всеми близлежащими точками (очень похожими лицами), вычисляет кратчайшие расстояния между всеми парами точек по получившейся сети и находит меньшее число координат, которое лучше всего приближает эти расстояния. В отличие от метода опорных векторов, координаты лиц в этом пространстве часто довольно осмысленны: одна координата может показывать, в каком направлении смотрит человек (левый профиль, поворот на три четверти, анфас и так далее), другая — как лицо выглядит (очень грустное, немного грустное, спокойное, радостное, очень радостное) и так далее. Isomap имеет неожиданную способность сосредоточиваться на самых важных измерениях комплекса данных — от понимания движения на видео до улавливания эмоций в речи.

Вот интересный эксперимент. Возьмите потоковое видео из глаз Робби, представьте, что каждый кадр — точка в пространстве изобра­жений, а потом сведите этот набор изображений к единственному измерению. Какое это будет измерение? Время. Как библиотекарь расставляет книги на полке, время ставит каждое изображение рядом с самыми похожими. Наверное, наше восприятие времени — просто естественный результат замечательной способности головного мозга понижать размерность. В дорожной сети нашей памяти время — главная автострада, и мы ее быстро находим. Другими словами, время — главная компонента памяти.

Жизнелюбивый робот

Кластеризация и понижение размерности приближают нас к пониманию человеческого обучения, но чего-то очень важного все равно не хватает. Дети не просто пассивно наблюдают за миром. Они активно действуют: замечают предметы, берут их в руки, играют, бегают, едят, плачут и задают вопросы. Даже самая продвинутая зрительная система будет бесполезна, если она не поможет Робби взаимодействовать со средой. Ему нужно не просто знать, где что находится, но и что надо делать в каждый момент. В принципе можно научить его выполнять пошаговые инструкции, соотнося показания сенсоров с соответству­ющими ответными действиями, но это возможно только для узких задач. Предпринимаемые действия зависят от цели, а не просто от того, что вы в данный момент воспринимаете, при этом цели могут быть весьма отдаленными. И потом, в любом случае нужно обойтись без пошагового контроля: дети учатся ползать, ходить и бегать сами, без помощи родителей. Ни один рассмотренный нами обучающий алгоритм так учиться не умеет.

У людей действительно есть один постоянный ориентир: эмоции. Мы стремимся к удовольствиям и избегаем боли. Коснувшись горячей плиты, вы непроизвольно отдернете руку. Это просто. Сложнее научиться не трогать плиту: для этого нужно двигаться так, чтобы избежать острой боли, которую вы еще не почувствовали. Головной мозг делает это, ассоциируя боль не просто с моментом прикосновения к плите, но и с ведущими к этому действиями. Эдвард Торндайк назвал это законом эффекта: действия, которые ведут к удовольствию, станут с большей вероятностью повторяться в будущем, а ведущие к боли — с меньшей. Удовольствие как будто путешествует назад во времени, и действия в конце концов могут начать ассоциироваться с довольно отдаленными результатами. Люди освоили такой поиск косвенных наград лучше, чем любое животное, и этот навык критически важен для успеха в жизни. В знаменитом эксперименте детям давали зефир и говорили, что, если они выдержат несколько минут и не съедят его, им дадут целых два. Те, кому это удалось, лучше успевали в школе и позже, когда стали взрослыми. Менее очевидно, наверное, то, что с аналогичной проблемой сталкиваются компании, использующие машинное обучение для совершенствования своих сайтов и методов ведения бизнеса. Компания может принять меры, которые принесут ей больше денег в краткосрочной перспективе — например, начать по той же цене продавать продукцию худшего качества, — но не обратить внимания, что в долгосрочной перспективе это приведет к потере клиентов.

Обучающиеся алгоритмы, которые мы видели в предыдущих главах, руководствуются немедленным удовлетворением: каждое действие, будь то выявление письма со спамом или покупка ценных бумаг, получает непосред­ственное поощрение или наказание от учителя. Но есть целый подраздел машинного обучения, посвященный алгоритмам, которые исследуют мир сами по себе: трудятся, сталкиваются с наградами, определяют, как получить их снова. Во многом они похожи на детей, которые ползают по комнате и тащат все в рот.

Это обучение с подкреплением, и этот принцип, скорее всего, станет активно использовать ваш первый домашний робот. Если вы распакуете Робби, включите его и попросите приготовить яичницу с беконом, у него с ходу может не получиться. Но когда вы уйдете на работу, он изучит кухню, отметит, где лежит утварь, какая у вас плита. Когда вы вернетесь, ужин будет готов.

Важным предшественником обучения с подкреплением была программа для игры в шашки, созданная ученым Артуром Сэмюэлом, работавшим в 1950-х годах в IBM. Настольные игры — прекрасный пример проблемы обучения с подкреплением: надо построить длинную последовательность ходов без какой-то обратной связи, а награда или наказание — победа или поражение — ждет в самом конце. Программа Сэмюэла оказалась способна научиться играть так не хуже большинства людей. Она не искала напрямую, какой ход сделать при каждом положении на доске (это было бы слишком сложно), а скорее училась оценивать сами положения — какова вероятность выигрыша, если начать с этой позиции? — и выбирать ходы, ведущие к наилучшему положению. Поначалу программа умела оценивать только конечные позиции: победа, ничья и поражение. Но раз определенные позиции означают победу, значит, позиции, из которых можно к ней прийти, хорошие. Томас Уотсон-старший, президент IBM, предсказал, что после презентации программы акции корпорации поднимутся на 15 пунктов. Так и произошло. Урок был усвоен, IBM развила успех и создала чемпионов по игре в шахматы и Jeopardy!.

Мысль, что не все состояния ведут к награде (положительной или отрицательной), но у каждого состояния имеется ценность, — центральный пункт обучения с подкреплением. В настольных играх награды есть только у конечных позиций (например, 1, 0 и –1 для победы, ничьей и поражения). Другие позиции не дают немедленной награды, но их ценность в том, что они могут обеспечить награду в будущем. Позиция в шахматах, из которой можно поставить мат в определенное количество ходов, практически так же хороша, как сама победа, и потому имеет высокую ценность. Такого рода рассуждения можно распространить вплоть до хороших и плохих дебютов, даже если на таком расстоянии от цели связь с наградой далеко не очевидна. В компьютерных играх награды обычно выражаются в очках, и ценность состояния — это количество очков, которые можно накопить, начиная с этого состояния. В реальной жизни отдача с задержкой менее выгодна, чем немедленная отдача, поэтому ее можно уменьшать на определенный процент, как это делается в случае инвестиций. Естественно, награда зависит от того, какие действия вы выберете, и цель обучения с подкреплением — всегда выбирать действие, ведущее к наибольшей награде. Стоит ли снять трубку и пригласить знакомую на свидание? Это может и положить начало чудесному роману, и привести к болезненному разочарованию. А если ваша подруга согласится на свидание, оно может пойти как удачно, так и неудачно. Надо каким-то образом абстрагироваться от бесконечных вариантов развития событий и принять решение. Обучение с подкреплением делает это путем оценки ценности каждого состояния — общей суммы наград, которых можно ожидать, начиная с него, — и выбора действий, которые ее максимизируют.

Представьте, что вы, как Индиана Джонс, пробираетесь по лабиринту и доходите до развилки. Карта подсказывает, что туннель слева ведет к сокро­вищнице, а справа — в яму со змеями. Ценность места, где вы стоите — прямо на распутье, — равна ценности сокровищ, потому что вы пойдете налево. Если всегда выбирать наилучшее возможное действие, ценность текущего состояния будет отличаться от ценности последу­ющего только непосредственной наградой за выполнение этого действия, если таковая имеется. Если известны непосредственные награды каждого состояния, можно использовать их для обновления ценности соседних состояний и так далее, пока значения всех состояний не будут согласованы: ценность сокровища распространяется назад по лабиринту до развилки и еще дальше. Зная ценность состояний, вы поймете, какое действие выбрать в каждом из них (то, которое дает максимальное сочетание немедленной награды и ценности результирующего состояния). Все это было открыто еще в 1950-е годы теоретиком управления Ричардом Беллманом. Однако настоящая проблема обучения с подкреплением появляется, когда карты местности у вас нет и остается только исследовать ее самостоятельно, определяя награды. Иногда получается найти драгоценности, иногда падаешь в яму со змеями. Каждое предпринятое действие дает информацию и о непосредственной награде, и о результирующем состоянии. Это можно сделать путем обучения с учителем. Однако нужно обновить и значение состояния, из которого вы только что пришли, чтобы привести его в соответствие с наблюдаемым значением, а именно суммой полученной награды и значения нового состояния, в котором вы оказались. Конечно, значение может пока быть неправильным, но, если достаточно долго ходить вокруг, в конце концов будут найдены правильные значения всех состояний и соответствующих действий. В этом в двух словах заключается обучение с подкреплением.

Обратите внимание, что обучение с подкреплением сталкивается с той же дилеммой изучения–применения, с которой мы познакомились в главе 5: чтобы максимизировать награды, вы, естественно, всегда хотите выбирать действие, ведущее к состоянию с наибольшим значением, но это не дает открыть потенциально большие награды в других местах. Алгоритмы обучения с подкреплением решают эту проблему, иногда выбирая лучшее действие, а иногда — случайное. (В головном мозге, кажется, для этого есть даже «генератор шумов».) На ранних этапах, когда можно получить много информации, имеет смысл больше изучать. Когда территория известна, лучше будет сосредоточиться на применении знания. Люди делают это на протяжении жизни: дети учатся, а взрослые используют (кроме ученых, которые похожи на вечных детей). Детская игра намного серьезнее, чем может показаться: если эволюция создала существо, которое в первые несколько лет своей жизни беспомощно и только обременяет родителей, такая расточительность должна давать большие преимущества. По сути, обучение с подкреплением — своего рода ускоренная эволюция, которая позволяет попробовать, отбросить и отточить действия в течение одной жизни, а не многих поколений, и по этим меркам оно крайне эффективно.

Начало серьезным исследованиям обучения с подкреплением положили в 1980-х годах работы Рича Саттона и Энди Барто из Массачусетского университета. Ученые чувствовали, что обучение в очень большой степени зависит от взаимодействия со средой, а контролирующие алгоритмы этого не улавливают, и нашли вдохновение в психологии обучения животных. Саттон продолжил заниматься этой темой и стал ведущим сторонником обучения с подкреплением. Еще один ключевой шаг был сделан в 1989 году, когда Крис Уоткинс из Кембриджа, которого изначально мотивировали экспериментальные наблюдения за обучением детей, пришел к современной формулировке обучения с подкреплением как оптимального контроля в неизвестной среде.

Тем не менее алгоритмы обучения с подкреплением, которые мы видели до сих пор, не очень реалистичны, потому что не знают, что делать в данном состоянии, если раньше в нем не были, а в реальном мире не бывает двух совершенно одинаковых ситуаций. Нужно уметь делать обобщения, выводя из посещенных состояний новые. К счастью, этому мы уже научились: достаточно просто обернуть обучение с подкреплением вокруг одного из алгоритмов обучения с учителем, с которыми мы познакомились раньше, например многослойного перцептрона. Теперь нейронная сеть будет предсказывать значение состояния, а сигналом ошибки для обратного распространения станет разница между предсказанными и наблюдаемыми значениями. Но есть и проблема. В обучении с учителем целевое значение состояния всегда одно и то же, а в обучении с подкреплением оно продолжает меняться в силу обновлений соседних состояний, поэтому обучение с подкреплением и обобщением часто не умеет приходить к стабильному решению, если только обуча­ющийся алгоритм внутри не простейший, например линейная функция. Несмотря на это, обучение с подкреплением в сочетании с нейронными сетями принесло ряд заметных успехов. Одним из первых достижений стала программа, играющая в нарды на уровне человека. Позже алгоритм обучения с подкреплением, разработанный в лондонском стартапе DeepMind, победил хорошего игрока в Pong и другие простые арка­ды. Для прогнозирования ценности действий на основе «сырых» пикселей экрана игровой приставки в нем использовалась глубокая сеть. Благодаря непрерывному зрению, обучению и контролю система имела как минимум поверхностное сходство с искусственным мозгом. Неудивительно, что Google заплатила за DeepMind полмиллиарда долларов, хотя у компании не имелось ни продукции, ни выручки и сотрудников было немного.

Кроме компьютерных игр, ученые использовали обучение с подкреплением для управления гимнастами — человечками из палочек, парковки задним ходом, пилотирования вертолетов вверх ногами, управления автоматическими телефонными диалогами, выделения каналов в сетях сотовой связи, вызова лифта, составления расписаний загрузки космического челнока и многих других целей. Обучение с подкреплением повлияло на психологию и нейробиологию. В мозге оно осуществляется благодаря нейромедиатору дофамину, который позволяет распространить разницу между ожидаемыми и фактическими наградами. Обучением с подкреплением можно объяснить условные рефлексы по Павлову, и, в отличие от бихевиоризма, такой подход допускает, что у животных есть внутренние психические состояния. Этот вид обучения используют пчелы-сборщицы и мыши, ищущие сыр в лабиринте. Человеческая повседневность — это поток почти незаметных чудес, которые возможны отчасти благодаря обучению с подкреплением. Вы встаете, одеваетесь, завтракаете, едете на работу, и все это автоматически, думая о чем-то другом. Где-то в глубине обучение с подкреплением постоянно дирижирует процессом и тонко настраивает удивительную симфонию движений. Элементы обучения с подкреплением, также называемые привычками, составляют большую часть наших действий: проголодался — идешь к холодильнику и берешь что-нибудь перекусить. Как показал Чарльз Дахигг в книге The Power of Habit, понимание и управление этим циклом намеков, рутинных действий и наград — ключ к успеху не только для отдельных людей, но и для бизнеса, и даже для общества в целом.

Из всех отцов обучения с подкреплением самый большой энтузиаст этого метода — Рич Саттон. Для него обучение с подкреплением — Верховный алгоритм, и решение этой проблемы равноценно решению проблемы искусственного интеллекта. C другой стороны, Крис Уоткинс не удовлетворен этим подходом и видит много того, что могут делать дети и не могут алгоритмы обучения с подкреплением: решать проблемы, решать их лучше после какого-то количества попыток, планировать, усваивать все более абстрактное знание. К счастью, для этих высоко­уровневых способностей у нас тоже есть обучающиеся алгоритмы, и самый важный из них — алгоритм образования фрагментов, или chunking.

Повторенье — мать ученья

Учиться — значит становиться лучше с практикой. Сейчас вы, может быть, и не помните, как сложно было научиться завязывать шнурки. Сначала не получалось вообще ничего, хотя вам было целых пять лет. Потом шнурки, наверное, развязывались быстрее, чем вы успевали их завязать. Но посте­пенно вы научились завязывать их быстрее и лучше, пока движения не стали совершенно автоматическими. То же самое происходило, например, с ползанием, ходьбой, бегом, ездой на велосипеде и вождением автомобиля, чтением, письмом и арифметикой, игрой на музыкальных инструментах и занятиями спортом, приготовлением пищи и работой на компьютере. По иронии судьбы, больше всего пользы приносит самое болезненное обучение: поначалу сложен каждый шаг, вы раз за разом терпите неудачу, и, даже если получается, результаты не впечатляют. Освоив замах в гольфе или подачу в теннисе, можно годами оттачивать мастерство, но все эти годы дадут меньше, чем первые несколько недель. С практикой вы становитесь искуснее, но скорость не постоянна: сначала улучшения приходят быстро, потом все медленнее, а затем совсем замедляются. Неважно, осваиваете вы игры или учитесь играть на гитаре: кривая зависимости улучшения результатов от времени — насколько хорошо вы что-то делаете и сколько времени это занимает — имеет очень характерную форму:

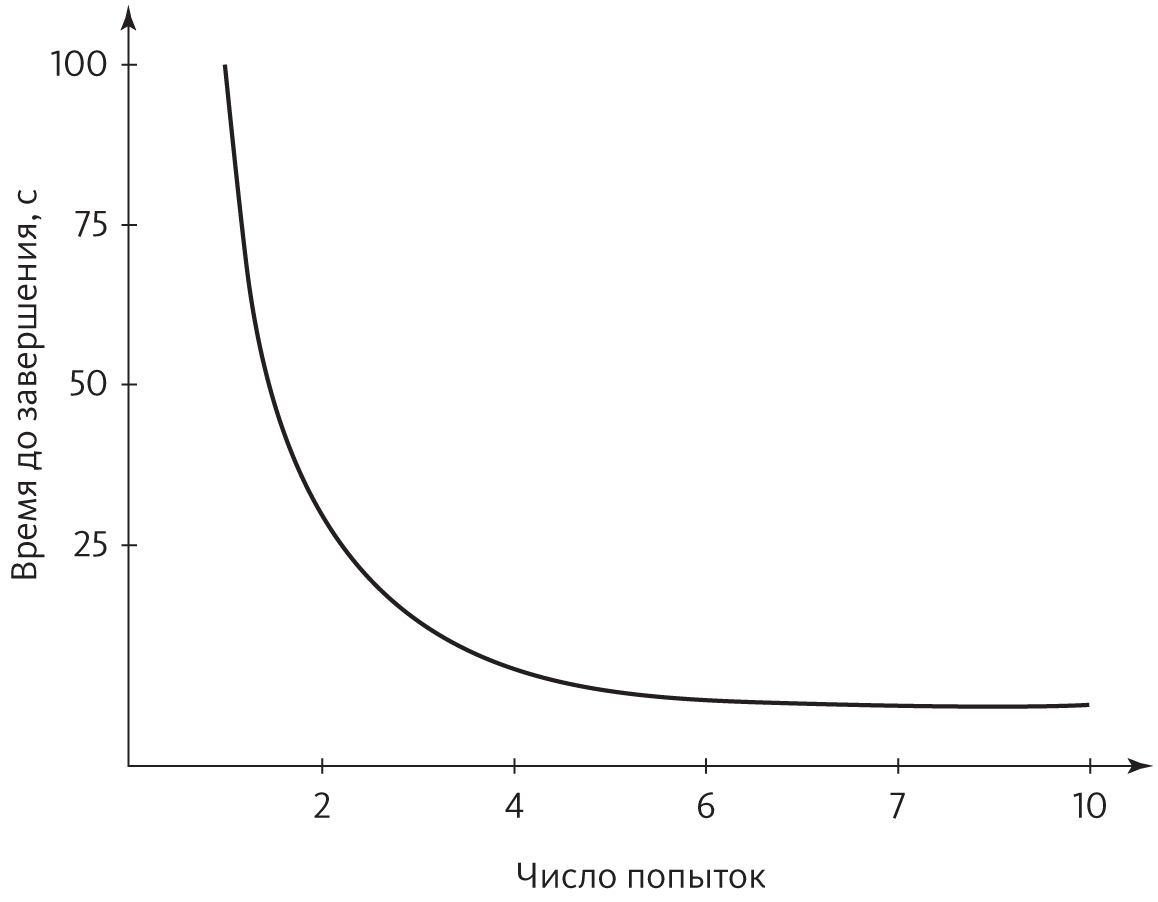
Этот тип кривой называют степенным законом, потому что изменение эффективности зависит от возведения времени в какую-то отрицательную степень. Например, на рисунке выше время до завершения пропорционально числу попыток, возведенному в минус вторую степень (или, эквивалентно, единице, разделенной на квадрат числа попыток). Практически все человеческие навыки следуют степенному закону, и разным умениям соответствуют разные степени. (А вот Windows с практикой не ускоряется — Microsoft есть над чем поработать.)

В 1979 году Аллен Ньюэлл и Пол Розенблюм начали задумываться, в чем причина так называемого степенного закона практики. Ньюэлл был одним из основателей науки об искусственном интеллекте и ведущим когнитивным психологом, а Розенблюм — его студентом в Университете Карнеги–Меллон. В то время ни одна из существу­ющих моделей практики не могла объяснить степенной закон. Ньюэлл и Розенблюм подозревали, что он как-то связан с образованием фрагментов — понятием из психологии восприятия и памяти. Информацию мы воспринимаем и запоминаем фрагментами и одномоментно можем удерживать в краткосрочной памяти лишь определенное количество таких кусочков (согласно классической статье Джорджа Миллера — семь, плюс-минус два). Критически важно, что группировка объектов позволяет обрабатывать намного больше информации, чем если бы мы этого не делали, поэтому в телефонных номерах ставят дефисы: 17-23-458-38-97 запомнить намного легче, чем 17234583897. Герберт Саймон, давний коллега Ньюэлла и один из основоположников изучения искусственного интеллекта, до этого открыл, что основное различие между начинающим и профессиональным шахматистом заключается в том, что новичок воспринимает шахматные позиции по одной за раз, в то время как профессионал видит более крупные паттерны, состоящие из многих элементов. Совершенствование шахматной игры в основном сводится к усвоению большего количества более крупных кусков. Ньюэлл и Розенблюм выдвинули гипотезу, что аналогичный процесс имеет место не только в шахматах, но и в усвоении навыков.

В восприятии и памяти фрагмент — это просто символ, который соответствует паттерну других символов: например, ИИ означает искусственный интеллект. Ньюэлл и Розенблюм адаптировали эту идею для теории решения проблем, уже разработанной Ньюэллом в соавторстве с Саймоном. Тогда в ходе эксперимента участников просили решать задачи, например выводить на доске одну математическую формулу из другой и одновременно вслух комментировать свои действия. Ученые выяснили, что человек решает проблемы путем разложения их на подпроблемы, подподпроблемы и так далее и систематически уменьшает различия между начальным состоянием (скажем, первой формулой) и целевым состоянием (второй формулой). Однако для того чтобы это сделать, надо найти рабочую последовательность действий, а на это требуется время. Гипотеза Ньюэлла и Розенблюма заключалась в том, что, решая подпроблему, мы каждый раз формируем фрагмент, который позволяет прямо перейти из состояния до решения в состояние после. Фрагмент в этом смысле состоит из двух частей: стимула (паттерна, который вы узнаёте во внешнем мире или в краткосрочной памяти) и реакции (последовательности действий, которую вы в результате выполняете). Полученный фрагмент хранится в долгосрочной памяти. В следующий раз, когда надо будет решить ту же подпроблему, можно будет легко применить его и сэкономить время на поиски. Это происходит на всех уровнях, пока не появится фрагмент для целой проблемы, позволяющий решить ее автоматически. Чтобы завязать шнурки, вы завязываете первый узел, делаете на одном конце петлю, оборачиваете вокруг нее другой конец и продеваете ее через петлю посередине. Каждое из этих действий для пятилетнего ребенка далеко не тривиально, но после усвоения соответствующих фрагментов дело почти сделано.

Розенблюм и Ньюэлл применили свою программу образования фрагментов для решения ряда проблем, измерили время, необходимое для каждой попытки, и — подумать только — получили ряд степенных кривых. Но это было только начало. Ученые встроили образование фрагментов в Soar — общую теорию познания, над которой Ньюэлл работал с Джоном Лэрдом, еще одним своим студентом. Программа Soar не действовала в рамках заданной иерархии целей — она умела определять новые подпроблемы и решать их каждый раз, когда сталкивалась с препятствием. Формируя новый фрагмент, Soar обобщала его, чтобы применить к схожим проблемам при помощи метода, похожего на обратную дедукцию. Образование фрагментов в Soar оказалось хорошей моделью не только для степенного закона практики, но и для многих феноменов обучения. Его можно было применять даже для получения нового знания путем разбивки данных на фрагменты и аналогии. Это привело Ньюэлла, Розенблюма и Лэрда к гипотезе, что образование фрагментов — единственный механизм, необходимый для обучения, иными словами — Верховный алгоритм.

Ньюэлл, Саймон, их студенты и последователи были классическими специалистами по искусственному интеллекту и твердо верили, что самое главное — решать проблемы. Обучающийся алгоритм может быть простым и ехать на закорках у мощного решателя задач. Действительно, обучение — просто еще один вид решения проблем. Ньюэлл и его соратники сосредоточили усилия на сведении всего обучения к образованию фрагментов, а всего познания — к Soar, но не достигли успеха. Проблема заключалась в следующем: по мере того как решатель задач узнавал все больше фрагментов, а сами фрагменты усложнялись, цена их проверки часто становилась слишком высокой, и программа не ускорялась, а замедлялась. Людям каким-то образом удается этого избежать, но ученые пока не разобрались, как именно. В довершение всего попытки свести обучение с подкреплением, обучение с учителем и все остальное к образованию фрагментов порождало больше проблем, чем решало. В итоге разработчики Soar признали поражение и встроили в программу другие типы обучения в качестве отдельных механизмов. Но, несмотря на это, разбивка на фрагменты остается выда­ющимся примером обучающегося алгоритма, вдохновенного психологией, и настоящий Верховный алгоритм, какой бы он ни был, несомненно будет уметь совершенствоваться с практикой.

Метод образования фрагментов и обучение с подкреплением используются в бизнесе не так широко, как обучение с учителем, класте­ризация и понижение размерности, но есть и более простой тип обучения путем взаимодействия со средой: определение последствий (и действие в соответствии с полученной информацией). Если домашняя страница вашего интернет-магазина голубого цвета и вы задумываетесь, не сделать ли ее красной для повышения продаж, протестируйте новый вариант на 100 тысячах случайно отобранных клиентов и сравните результаты с теми, кто видел обычный сайт. Эту методику, называемую A/B-тестированием, поначалу применяли в основном при испытаниях лекарств, но с того времени она распространилась на многие области, где данные под рукой — от маркетинга до предоставления помощи иностранным государствам. Его можно обобщить для одновременной проверки многих сочетаний изменений, не запутываясь, какие изменения ведут к каким приобретениям (или потерям). Amazon, Google и другие компании верят этому тестированию безгранично. Вы, скорее всего, сами того не подозревая, участвовали в тысячах A/B-тестов. Этот метод показывает ошибочность расхожего мнения, что большие данные хороши для нахождения корреляций, но не причинно-следственных связей. Если оставить в стороне философские тонкости, определение причинности — нахождение последствий действий, и оно доступно каждому — от годовалого ребенка, который плещется в ванночке, и до президента, ведущего кампанию по переизбранию, — был бы поток данных, на который есть возможность влиять.

Как найти соотношения

Если мы одарим нашего Робби всеми способностями к обучению, которые до сих пор видели в этой книге, он будет достаточно умным, но немного аутич­ным. Мир для него окажется скоплением отдельных предметов: он начнет узнавать их, манипулировать ими и даже делать в их отношении прогнозы, но не будет понимать, что мир — это сеть взаимосвязей. Робби-врач станет ставить диагнозы человеку с гриппом на основе симптомов, но не заподозрит свиной грипп на том основании, что пациент контактировал с носителем вируса. До появления Google поисковые движки решали, соответствует ли веб-страница вашему запросу, заглядывая в ее содержимое, — что еще можно сделать? Идея Брина и Пейджа заключалась в том, что самый сильный признак, указывающий на то, что страница подходит, — это ссылки на нее с других подходящих страниц. Аналогично, если вы хотите предсказать, рискует ли подросток начать курить, — лучшее, что вы можете сделать, — проверить, курят ли его близкие друзья. Форма фермента неотделима от формы молекул, которые он переносит, как замок неотделим от ключа. Хищника и жертву объединяют сильно взаимосвязанные свойства, каждое из которых эволюционировало, чтобы победить соперника. Во всех этих случаях лучший способ понять сущность — будь то человек, животное, веб-страница или молекула, — понять, как она связана с другими сущностями. Для этого требуется новый род обучения, который относится к данным не как к случайной выборке не связанных друг с другом объектов, а как к возможности взглянуть на сложную сеть. Узлы в этой сети взаимодействуют: то, что вы делаете с одним, влияет на другие и возвращается, чтобы повлиять на вас. Реляционные обучающиеся алгоритмы, как они называются, могут не иметь социальных навыков, но близки к этому. В традиционном статистическом обучении каждый человек как остров, вещь в себе. В реля­ционном обучении люди — кусочки континента, часть главного. Они реляционные обучающиеся алгоритмы, связанные и подключенные друг к другу, и, если мы хотим, чтобы Робби вырос восприимчивым, социально адаптированным роботом, его тоже надо подключить.

Первая сложность, с которой мы сталкиваемся, заключается в следующем: если данные образуют одну большую сеть, вместо большого числа примеров для обучения у нас, видимо, будет всего один, а этого недостаточно. Наивный байесовский алгоритм узнает, что высокая температура — один из симпто­мов гриппа, путем подсчета больных гриппом пациентов с лихорадкой. На основе одного случая он либо сделает вывод, что грипп всегда вызывает высокую температуру, либо что он никогда ее не вызывает. И то и другое ложно. Мы хотели бы определить, что грипп — заразная болезнь, посмотрев на паттерны инфекции в социальной сети — группа зараженных людей тут, группа незараженных там, — но посмотреть мы можем только на один паттерн, даже если он представляет собой сеть из семи миллиардов людей, поэтому неясно, как тут делать обобщения. Ключ к решению — обратить внимание на то, что при погружении в большую сеть в нашем распоряжении оказывается много примеров пар. Если у пары знакомых выше вероятность заболеть гриппом, чем у пары людей, которые никогда не встречались, то знакомство с заболевшим делает и вас уязвимее для этой болезни. К сожалению, не получится просто посчитать в име­ющихся данных пары знакомых, где оба больны гриппом, и превратить результат в вероятность. Дело в том, что знакомых у людей много и все парные вероятности не сложатся в связную модель, которая позволит, например, вычислить риск гриппа, зная, какие знакомые больны. Когда примеры не были связаны между собой, этой проблемы не возникало: ее не будет, скажем, в обществе бездетных пар, каждая из которых живет на собственном необитаемом острове. Но такой мир нереален, и эпидемий в нем не появится в любом случае.

Решение заключается в том, чтобы получить набор свойств и узнать их вес, как в сетях Маркова. Для каждого человека X можно ввести свойство «X болен гриппом», для каждой пары знакомых X и Y — свойство «и X, и Y больны гриппом» и так далее. Как и в марковских сетях, максимально правдоподобный вес будет заставлять свойство встречаться с частотой, наблюдаемой в данных. Вес «X болен гриппом» будет высоким, если много людей больны гриппом. Вес «и X, и Y больны гриппом» окажется выше, если шанс заболеть гриппом у Y с больным знакомым X выше, чем у случайно выбранного члена сети. Если 40 процентов людей и 16 процентов всех пар знакомых больны гриппом, вес свойства «и X, и Y больны гриппом» будет нулевым, потому что для правильного воспроизведения статистики данных (0,4 × 0,4 = 0,16) это свойство не нужно. Однако если вес свойства положительный, грипп с большей вероятностью будет возникать в группах, а не произвольно инфицировать людей, и вероятность заболеть гриппом станет выше, если больны знакомые.

Обратите внимание, что сеть имеет отдельное свойство для каждой пары — «и у Элис, и у Боба грипп», «и у Элис, и у Криса грипп» и так далее. Но узнать вес для каждой пары не получится, потому что для пары есть только одна точка данных (инфицированы или нет) и нельзя сделать обобщение для членов сети, которым мы еще не поставили диагноз (есть ли грипп и у Иветт, и у Зака?). Вместо этого мы можем узнать единичный вес для всех свойств такой формы на основе всех частных случаев, которые наблюдали. В результате «и X, и Y больны гриппом» будет шаблоном свойств, который можно применить к каждой паре знакомых (Элис и Бобу, Элис и Крису и так далее). Веса для всех частных случаев шаблона связаны в том смысле, что у них всех будет одинаковое значение, и таким образом обобщение окажется возможным, несмотря на то что пример у нас всего один (сеть в целом). В нереляционном обучении параметры модели связаны только одним способом: по всем независимым примерам (например, все пациенты, которым мы поставили диагноз). В реляционном обучении каждый шаблон свойств, который мы создаем, связывает параметры всех его частных случаев.

Мы не ограничены парными или индивидуальными свойствами. Facebook хочет выявить ваших потенциальных друзей, чтобы порекомендовать их вам. Для этого используется правило «Друзья друзей, вероятно, тоже друзья», а каждый частный случай этого правила включает троих: если Элис и Боб — друзья, и Боб и Крис — друзья, то Элис и Крис — потенциальные друзья. В шутке Генри Менкена о том, что мужчина богат, когда он зарабатывает больше мужа сестры своей жены, присутствует упоминание о четырех людях. Каждое из этих правил можно превратить в шаблон свойств реляционной модели, а вес для них можно получить на основе того, как часто свойство встречается в данных. Как и в марковских сетях, сами свойства тоже можно вывести из данных.

Реляционные обучающиеся алгоритмы способны переносить обобщения из одной сети в другую (например, получить модель распространения гриппа в Атланте и применить ее в Бостоне) и учиться на нескольких сетях (например, для Атланты и Бостона при нереалистичном допущении, что в Атланте никто никогда не контактировал с бостонцами). В отличие от «традиционного» обучения, где все примеры должны иметь одинаковое количество атрибутов, в реляционном обучении размер сетей может быть разным: более крупная сеть просто будет содержать больше частных случаев тех же шаблонов, что и меньшая. Конечно, перенос обобщения из меньшей сети в большую может быть точным, а может и не быть, но смысл в том, что ничто не мешает это делать, а крупные сети локально часто ведут себя как небольшие.

Самый изящный трюк, на который способен реляционный обуча­ющийся алгоритм, — превратить периодического учителя в неутомимого. Для обычного классификатора примеры без классов бесполезны: если я узнаю симптомы пациентов, но не их диагнозы, это не поможет мне научиться диагностике. Однако если мне известно, что кто-то из друзей пациента болен гриппом, это косвенный признак, что грипп может быть и у него. Поставить диагноз нескольким людям в сети, а затем распространить его на их знакомых и знакомых их знакомых — тоже неплохо, хотя и хуже, чем индивидуальный диагноз. Полученные таким образом диагнозы могут быть зашумленными, но общая статистика корреляции симптомов с гриппом будет, вероятно, намного точнее и полнее, чем выводы на основе горсти изолированных диагнозов. Дети очень хорошо умеют извлекать максимальную пользу из периодического надзора за ними (при условии, что они его не про­игнорируют). Реляционные обучающиеся алгоритмы частично обладают такой способностью.

Однако за мощь приходится платить. В обычных классификаторах, например дереве решений или перцептроне, вывод о классе объекта на основе его атрибутов можно сделать после нескольких просмотров данных и небольших арифметических вычислений. В случае сети класс каждого узла косвенно зависит от всех остальных узлов, и сделать о нем вывод изолированно нельзя. Можно прибегнуть к тем же видам методик логического вывода, что и в случае байесовских сетей, например к циклическому распространению доверия или MCMC, но масштаб будет другим: в типичной байесовской сети могут быть тысячи переменных, а в социальных сетях — миллионы и даже больше узлов. К счастью, модель сети состоит из многократных повторений одних и тех же черт с теми же самыми весами, поэтому часто получается сжать сеть в «сверхузлы», состоящие из многочисленных узлов, которые, как мы знаем, имеют одинаковые вероятности, и теперь нужно решить намного меньшую проблему с тем же результатом.

У реляционного обучения долгая история, уходящая как минимум в символистские методики 1970-х годов, например обратную дедукцию. Но с зарождением интернета оно приобрело новый импульс. Сети внезапно стали повсеместными, а их моделирование — неотложной задачей. Явление, которое мне показалось особенно любопытным, — сарафанное радио. Как распространяется информация в социальной сети? Можно ли измерить влияние каждого ее участника и породить волну слухов, нацелившись на минимально необходимое число наиболее влиятельных? С моим студентом Мэттом Ричардсоном мы разработали алгоритм, который делал именно это, и применили его к сайту с обзорами продукции, где пользователи имели возможность рассказывать, чьим обзорам они доверяют. Помимо всего прочего, мы обнаружили, что рекламировать продукты одному самому влиятельному члену, которому доверяют многие участники сети, которым, в свою очередь, доверяют многие другие пользователи и так далее, — не менее эффективный метод, чем маркетинг, направленный на треть всех пользователей по отдельности. Затем последовала целая лавина исследований этой проблемы. С тех пор я применял реляционное обучение ко многим другим задачам, включая прогнозирование, кто будет образовывать связи в социальной сети, интегрирование баз данных и способности роботов картировать окружающую обстановку.

Если вы хотите понять, как работает мир, реляционное обучение стоит иметь в арсенале. В цикле романов Айзека Азимова «Основание» ученому Гэри Селдону удается математически предсказать будущее человечества и тем самым спасти его от упадка. Пол Кругман, наряду с другими, признался, что эта соблазнительная мечта сделала его экономистом. Согласно Селдону, люди похожи на молекулы газа, и, даже если сами индивидуумы непредсказуемы, на общества это не распространяется просто по закону больших чисел. Реляционное обучение объясняет, почему это не так. Если бы люди были независимы и каждый принимал решения изолированно, общества действительно были бы предсказуемы, потому что случайные решения складывались бы в довольно постоянное среднее. Но когда люди взаимодействуют, более крупные группы бывают не более, а менее предсказуемы, чем небольшие. Если уверенность и страх заразны, каждое из этих состояний станет некоторое время доминировать, но периодически все общество будет качать от одного к другому. Это, однако, совсем не так уж плохо. Если получится измерить, как сильно люди влияют друг на друга, можно оценить и то, сколько времени пройдет перед таким сдвигом, даже если он произойдет впервые. Это еще один способ, благодаря которому «черные лебеди» не обязательно непредсказуемы.

Многие жалуются, что чем больше объем данных, тем легче увидеть в них мнимые паттерны. Может быть, это и правда, если данные представляют собой просто большой набор не связанных друг с другом объектов, но, если они взаимосвязаны, картина меняется. Например, критики применения добычи данных для борьбы с терроризмом утверждают, что, даже если не брать этические аспекты, такой подход не сработает, потому что невинов­ных слишком много, а террористов слишком мало, и поиск подозрительных паттернов либо даст много ложных срабатываний, либо никого не поймает. Человек, снимающий на видеокамеру ратушу Нью-Йорка, — это турист или злоумышленник, присматривающий место для теракта? А человек, заказавший большую партию нитрата аммония, — мирный фермер или изготовитель взрывных устройств? Все эти факты по отдельности выглядят достаточно безобидно, но, если «турист» и «фермер» часто разговаривают по телефону и последний только что въехал тяжело груженным пикапом на Манхэттен, наверное, самое время к ним присмотреться. Агентство национальной безопасности США любит искать данные в списках телефонных разговоров не потому, что это, вероятно, законно, а потому, что эти списки зачастую более информативны для предсказывающих алгоритмов, чем содержание самих звонков, которое должен оценивать живой сотрудник.

Кроме социальных сетей, «приманка» реляционного обучения — возможность разобраться в механизмах работы живой клетки. Клетка — сложная метаболическая сеть, где гены кодируют белки, регулирующие другие гены. Это длинные, переплетающиеся цепочки химических реакций, продукты, мигрирующие из одной органеллы в другую. Независимых сущностей, которые делают свою работу изолированно, там не найти. Лекарство от рака должно нарушить функционирование раковой клетки, не мешая работе нормальных. Если у нас в руках окажется точная реляционная модель обоих случаев, можно будет попробовать много разных лекарств in silico, разрешая модели делать выводы об их положительных и отрицательных эффектах, и, выбрав только хорошие, испытать их in vitro и, наконец, in vivo.

Как и человеческая память, реляционное обучение плетет богатую сеть ассоциаций. Оно соединяет воспринимаемые объекты, которые робот вроде Робби может усвоить путем кластеризации и уменьшения размерности, с навыками, которые можно приобрести путем подкреп­ления и образования фрагментов, а также со знанием более высокого уровня, которое дают чтение, учеба в школе и взаимодействие с людьми. Реляционное обучение — последний кусочек мозаики, заключительный ингредиент, который нужен нам для нашей алхимии. Теперь пришло время отправиться в лабораторию и превратить эти элементы в Верховный алгоритм.

Отправить