ГЛАВА 4

КАК УЧИТСЯ НАШ МОЗГ?

С момента своего открытия правило Хебба — краеугольный камень коннекционизма. Своим названием это научное направление обязано представлению, что знания хранятся в соединениях между нейронами. В вышедшей в 1949 году книге The Organization of Behavior («Организация поведения») канадский психолог Дональд Хебб описывал это следующим образом: «Если аксон клетки A расположен достаточно близко к клетке B и неоднократно или постоянно участвует в ее стимуляции, то в одной или обеих клетках будут иметь место процессы роста или метаболические изменения, которые повышают эффективность возбуждения клеткой A клетки B». Это утвержде­ние часто перефразируют как «нейроны, которые срабатывают вместе, связываются друг с другом».

В правиле Хебба слились идеи психологии, нейробиологии и немалая доля домыслов. Ассоциативное обучение было любимой темой британских эмпириков начиная с Локка, Юма и Джона Стюарта Милля. В Principles of Psychology («Принципы психологии») Уильям Джеймс сформулировал общий принцип ассоциации, который замечательно похож на правило Хебба, но вместо нейронов в нем присутствуют процессы в головном мозге, а вместо эффективности стимуляции — распространение возбуждения. Примерно в то же самое время великий испанский нейробиолог Сантьяго Рамон-и-Кахаль провел первые подробные исследования мозга, окрашивая нейроны по недавно изобретенному методу Гольджи, и каталогизировал свои наблюдения, как ботаники классифицируют новые виды деревьев. Ко времени Хебба нейро­биологи в общих чертах понимали, как работают нейроны, однако именно он первым предложил механизм, согласно которому нейроны могут кодировать ассоциации.

В символистском обучении между символами и понятиями, которые они представляют, существует однозначное соответствие. Коннекционистские же представления распределены: каждое понятие представлено множеством нейронов, и каждый нейрон участвует в представлении многих концепций. Нейроны, которые возбуждают друг друга, образуют, в терминологии Хебба, «ансамбли клеток». С помощью таких собраний в головном мозге представлены понятия и воспоминания. В каждый ансамбль могут входить нейроны из разных областей мозга, ансамбли могут пересекаться. Так, клеточный ансамбль для понятия «нога» включает ансамбль для понятия «ступня», в который, в свою очередь, входят ансамбли для изображения ступни и звучания слова «ступня». Если вы спросите символистскую систему, где находится понятие «Нью-Йорк», она укажет точное место его хранения в памяти. В коннекционистской системе ответ будет «везде понемногу».

Еще одно отличие между символистским и коннекционистским обучением заключается в том, что первое — последовательное, а второе — параллельное. В случае обратной дедукции мы шаг за шагом разбираемся, какое правило необходимо ввести, чтобы от посылок прийти к желаемым выводам. В коннекционистской модели все нейроны учатся одновременно, согласно правилу Хебба. В этом нашли отражение различия между компьютерами и мозгом. Компьютеры даже совершенно обычные операции — например, сложение двух чисел или переключение выключателя — делают маленькими шажочками, поэтому им нужно много этапов. При этом шаги могут быть очень быстрыми, потому что транзисторы способны включаться и выключаться миллиарды раз в секунду. Мозг же умеет выполнять большое количество вычислений параллельно благодаря одновременной работе миллиардов нейронов. При этом нейроны могут стимулироваться в лучшем случае тысячу раз в секунду, и каждое из этих вычислений медленное.

Количество транзисторов в компьютере приближается к количеству нейронов в головном мозге человека, однако мозг безусловно выигрывает в количестве соединений. Типичный транзистор в микропроцессоре не­посредственно связан лишь с немногими другими, и применяемая технология планарных полупроводников жестко ограничивает потенциал совершенствования работы компьютера. А у нейрона — тысячи синапсов. Если вы идете по улице и увидели знакомую, вам понадобится лишь десятая доля секунды, чтобы ее узнать. Учитывая скорость переключения нейронов, этого времени едва хватило бы для сотни шагов обработки информации, но за эти сотни шагов мозг способен просканировать всю память, найти в ней самое подходящее и адаптировать найденное к новому контексту (другая одежда, другое освещение и так далее). Каждый шаг обработки может быть очень сложным и включать большой объем информации.

Это не значит, что с помощью компьютера нельзя симулировать работу мозга: в конце концов, именно это делают коннекционистские алгоритмы. Поскольку компьютер — универсальная машина Тьюринга, он может выполнять вычисления, происходящие в мозге, как и любые другие, при условии, что у него есть достаточно памяти и времени. В частности, недостаток связности можно компенсировать скоростью: использовать одно и то же соединение тысячу раз, чтобы имитировать тысячу соединений. На самом деле сегодня главный недостаток компьютеров заключается в том, что в отличие от мозга они потребляют энергию: ваш мозг использует примерно столько мощности, сколько маленькая лампочка, в то время как электричеством, питающим компьютер Watson, о котором мы рассказывали выше, можно осветить целый бизнес-центр.

Тем не менее для имитации работы мозга одного правила Хебба мало: сначала надо разобраться с устройством головного мозга. Каждый нейрон напоминает крохотное деревце с огромной корневой системой из дендритов и тонким волнистым стволом — аксоном. Мозг в целом похож на лес из миллиардов таких деревьев, однако лес этот необычный: ветви деревьев соединены в нем с корнями тысяч других деревьев (такие соединения называются синапсами), образуя колоссальное, невиданное хитросплетение. У одних нейронов аксоны короткие, у других — чрезвычайно длинные, простирающиеся от одного конца мозга к другому. Если расположить аксоны мозга друг за другом, они займут расстояние от Земли до Луны.

Эти джунгли потрескивают от электрических разрядов. Искры бегут по стволам и порождают в соседних деревьях еще больший сонм искр. Время от времени лес неистово вспыхивает, потом снова успокаивается. Когда человек шевелит пальцем на ноге, серии электрических разрядов — так называемых потенциалов действия — бегут вниз по спинному мозгу, пока не достигнут мышц пальца и не прикажут ему двигаться. Работа мозга похожа на симфонию таких электрических разрядов. Если бы можно было посмотреть изнутри на то, что происходит в тот момент, когда вы читаете эту страницу, сцена затмила бы самые оживленные мегаполисы из фантасти­ческих романов. Этот невероятно сложный узор нейронных искр в итоге порождает человеческое сознание.

Во времена Хебба еще не умели измерять силу синапсов и ее изме­нения, не говоря уже о том, чтобы разбираться в молекулярной биологии синап­тических процессов. Сегодня мы знаем, что синапсы возникают и развиваются, когда вскоре после пресинаптических нейронов возбуждаются постсинаптические. Как и во всех других клетках, концентрация ионов внутри и за пределами нейрона отличается, и из-за этого на клеточной мембране имеется электрическое напряжение. Когда пресинаптический нейрон возбуждается, в синаптическую щель выделяются крохотные пузырьки с молекулами нейротрансмиттеров. Они заставляют открыться каналы в мембране постсинаптического нейрона, из которых выходят ионы калия и натрия, меняющие напряжение на мембране. Если одновременно возбуж­дается достаточное количество близко расположенных пресинаптических нейронов, напряжение подскакивает и по аксону постсинаптического нейрона проходит потенциал действия. Благодаря этому ионные каналы становятся восприимчивее, а также появляются новые, усиливающие синапс каналы. Насколько нам известно, нейроны учатся именно так.

Следующий шаг — превратить все это в алгоритм.

Взлет и падение перцептрона

Первая формальная модель нейрона была предложена в 1943 году Уорреном Маккаллоком и Уолтером Питтсом. Она была во многом похожа на логические вентили, из которых состоят компьютеры. Вентиль ИЛИ включается, когда как минимум один из его входов включен, а вентиль И — когда включены все. Нейрон Маккаллока–Питтса включается, когда количество его активных входов превышает определенное пороговое значение. Если порог равен единице, нейрон действует как вентиль ИЛИ. Если порог равен числу входов — как вентиль И. Кроме того, один нейрон Маккаллока–Питтса может не давать включаться другому: это моделирует и ингибирующие синапсы, и вентиль НЕ. Таким образом, нейронные сети могут совершать все операции, которые умеет делать компьютер. Поначалу компьютер часто называли электронным мозгом, и это была не просто аналогия.

Однако нейрон Маккаллока–Питтса не умеет учиться. Для этого соединениям между нейронами надо присвоить переменный вес, и в результате получится так называемый перцептрон. Перцептроны были изобретены в конце 1950-х Фрэнком Розенблаттом, психологом из Корнелльского университета. Харизматичный оратор и очень живой человек, Розенблатт сделал для зарождения машинного обучения больше, чем кто бы то ни было. Своим названием перцептроны обязаны его интересу к применению своих моделей в проблемах восприятия (перцепции), например распознавания речи и символов. Вместо того чтобы внедрить перцептроны в компьютерные программы, которые в те дни были очень медлительными, Розенблатт построил собственные устройства: вес был представлен в них в виде пере­менных резисторов, как те, что стоят в переключателях с регулируемой яркостью, а для взвешенного обучения использовались электромоторы, которые крутили ручки резисторов. (Как вам такие высокие технологии?)

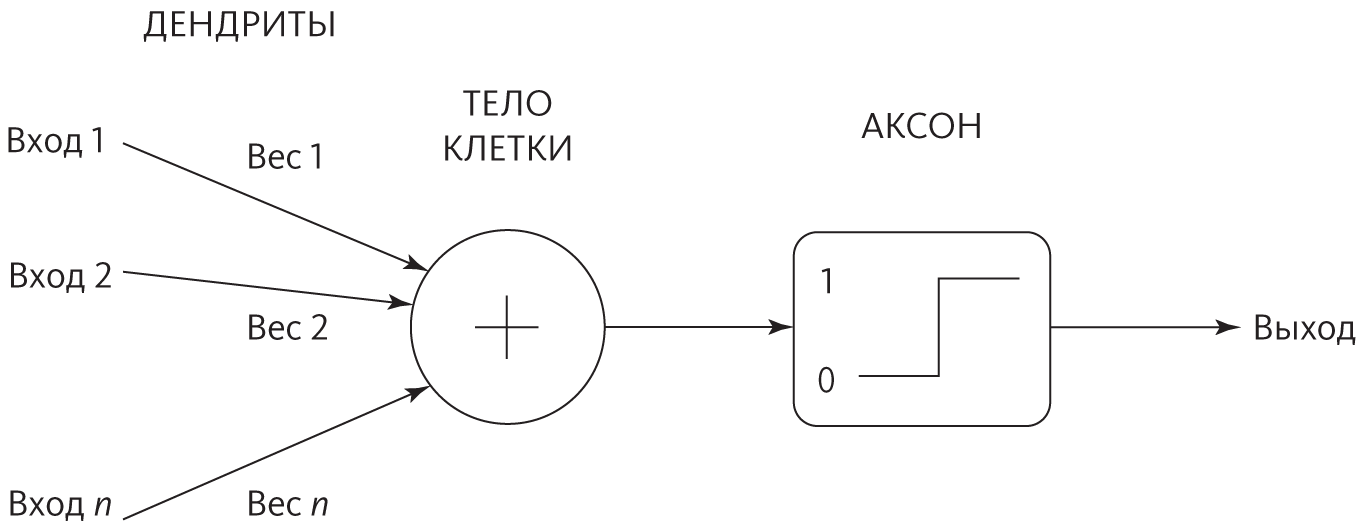
В перцептроне положительный вес представляет возбуждающее соединение, а отрицательный — ингибирующее. Если взвешенная сумма входов перцептрона выше порогового значения, он выдает единицу, а если ниже — ноль. Путем варьирования весов и порогов можно изменить функцию, которую вычисляет перцептрон. Конечно, много подробностей работы нейронов игнорируется, но ведь мы хотим все максимально упростить, и наша цель — не построить реалистичную модель мозга, а разработать обучающийся алгоритм широкого применения. Если какие-то из проигнорированных деталей окажутся важными, их всегда можно будет добавить. Несмотря на все упрощения и абстрактность, можно заметить, что каждый элемент этой модели соответствует элементу нейрона:

Чем больше вес входа, тем сильнее соответствующий синапс. Тело клетки складывает все взвешенные входы, а аксон применяет к результату ступенчатую функцию. На рисунке в рамке аксона показан график ступенчатой функции: ноль для низких значений входа резко переходит в единицу, когда вход достигает порогового значения.

Представьте, что у перцептрона есть два непрерывных входа x и y (это значит, что x и y могут принимать любые числовые значения, а не только 0 и 1). В таком случае каждый пример можно представить в виде точки на плоскости, а границей между положительными (для которых перцептрон выдает 1) и отрицательными (выход 0) примерами будет прямая линия:

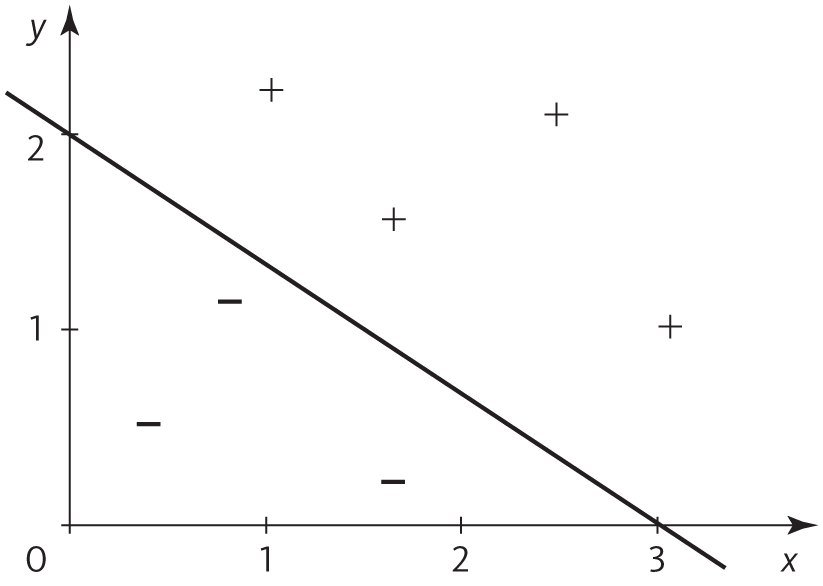
Дело в том, что граница — это ряд точек, в которых взвешенная сумма точно соответствует пороговому значению, а взвешенная сумма — линейная функция. Например, если вес x — 2, вес y — 3, а порог — 6, граница будет задана уравнением 2x + 3 = 6. Точка x = 0, y = 2 лежит на границе, и, чтобы удержаться на ней, нам надо делать три шага вперед для каждых двух шагов вниз: тогда прирост x восполнит уменьшение y. Полученные в результате точки образуют прямую.

Нахождение весов перцептрона подразумевает варьирование направления прямой до тех пор, пока с одной стороны не окажутся все положительные примеры, а с другой — все отрицательные. В одном измерении граница — это точка, в двух измерениях — прямая, в трех — плоскость, а если измерений больше трех — гиперплоскость. Визуализировать что-то в гиперпространстве сложно, однако математика в нем работает точно так же: в n измерениях у нас будет n входов, а у перцептрона — n весов. Чтобы решить, срабатывает перцептрон или нет, надо умножить каждый вес на значение соответству­ющего входного сигнала и сравнить их общую сумму с пороговым значением.

Если веса всех входов равны единице, а порог — это половина числа вхо­дов, перцептрон сработает в случае, если срабатывает больше половины входов. Иными словами, перцептрон похож на крохотный парламент, в котором побеждает большинство (хотя, наверное, не такой уж и крохотный, учитывая, что в нем могут быть тысячи членов). Но при этом парламент не совсем демократический, поскольку в целом не все имеют равное право голоса. Нейронная сеть в этом отношении больше похожа на Facebook, потому что несколько близких друзей стоят тысячи френдов, — именно им вы больше всего доверяете, и они больше всего на вас влияют. Если друг порекомендует вам фильм, вы посмотрите его и вам понравится, в следующий раз вы, вероятно, снова последуете его совету. С другой стороны, если подруга постоянно восторгается фильмами, которые не доставляют вам никакого удовольствия, вы начнете игнорировать ее мнение (и не исключено, что дружба поостынет).

Именно так алгоритм перцептрона Розенблатта узнает вес входов.

Давайте рассмотрим «бабушкину клетку», излюбленный мысленный эксперимент когнитивных нейробиологов. «Бабушкина клетка» — это нейрон в вашем мозге, который возбуждается тогда и только тогда, когда вы видите свою бабушку. Есть ли такая клетка на самом деле — вопрос открытый, но давайте изобретем ее специально для машинного обучения. Перцептрон учится узнавать бабушку следующим образом. Входные сигналы для этой клетки — либо необработанные пиксели, либо различные жестко прошитые свойства изображения, например карие глаза: вход будет равен 1, если на изображении есть карие глаза, и 0 — если нет. Вначале вес всех соединений, ведущих от свойств к нейронам, маленький и произвольный, как у синапсов в мозге новорожденного. Затем мы показываем перцептрону ряд картинок: на одних есть ваша бабушка, а на других нет. Если перцептрон срабатывает при виде бабушки или не срабатывает, когда видит кого-то еще, значит, никакого обучения не нужно (не чини то, что работает). Но если перцептрон не срабатывает, когда смотрит на бабушку, это значит, что взвешенная сумма значений его входов должна быть выше и веса активных входов надо увеличить (например, если бабушка кареглазая, вес этой черты повысится). И наоборот, если перцептрон срабатывает, когда не надо, веса активных входов следует уменьшить. Ошибки — двигатель обучения. Со временем черты, которые указывают на бабушку, получат большой вес, а те, что не указывают, — маленький. Как только перцептрон начнет всегда срабатывать при виде вашей бабушки и ошибочные срабатывания исчезнут, обучение завершится.

Перцептрон вызвал восторг в научном сообществе. Он был простым, но при этом умел узнавать печатные буквы и звуки речи: для этого требовалось только обучение на примерах. Коллега Розенблатта по Корнелльскому университету доказал: если положительные и отрицательные примеры можно разделить гиперплоскостью, перцептрон эту плоскость найдет. Розенблатту и другим ученым казалось вполне достижимым истинное понимание принципов, по которым учится мозг, а с ним — мощный много­целевой обучающийся алгоритм.

Но затем перцептрон уперся в стену. Инженеров знаний раздражали заявления Розенблатта: они завидовали вниманию и финансированию, которое привлекали нейронные сети в целом и перцептроны в частности. Одним из таких критиков был Марвин Минский, бывший одноклассник Розенблатта по Научной средней школе в Бронксе, руководивший к тому времени группой искусственного интеллекта в Массачусетском технологическом институте. (Любопытно, что его диссертация была посвящена нейронным сетям, но потом он в них разочаровался.) В 1969 году Минский и его коллега Сеймур Пейперт опубликовали книгу Perceptrons: an Introduction to Computational Geometry, где подробно, один за другим описали простые вещи, которым одноименный алгоритм не в состоянии научиться. Самый простой и потому самый убийственный пример — это функция «исключающее ИЛИ» (сокращенно XOR), которая верна, если верен один, но не оба входа. Например, две самые лояльные группы покупателей продукции Nike — это, видимо, мальчики-подростки и женщины среднего возраста. Другими словами, вы, скорее всего, купите кроссовки Nike, если вы молоды XOR женщина. Молодость подходит, женский пол тоже, но не оба фактора сразу. Если вы не молоды и вы не женщина, для рекламы Nike вы тоже неперспективная цель. Проблема с XOR в том, что не существует прямой линии, способной отделить положительные примеры от отрицательных. На рисунке показаны два неподходящих кандидата:

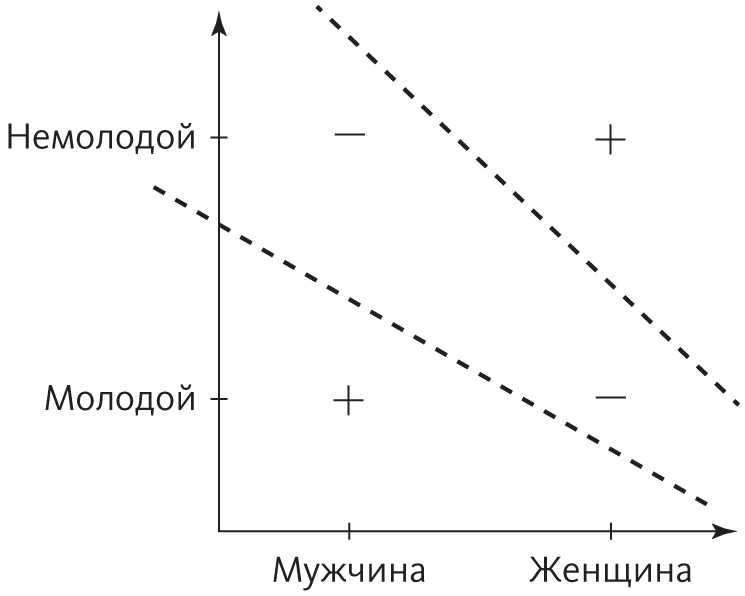
Поскольку перцептроны могут находить только линейные границы, XOR для них недоступен, а если они неспособны даже на это, значит, перцептрон — не лучшая модель того, как учится мозг, и неподходящий кандидат в Верховные алгоритмы.

Перцептрон моделирует только обучение отдельного нейрона. Минский и Пейперт признавали, что слои взаимосвязанных нейронов должны быть способны на большее, но не понимали, как такие слои обучить. Другие ученые тоже этого не знали. Проблема в том, что не существует четкого способа изменить вес нейронов в «скрытых» слоях, чтобы уменьшить ошибки нейронов в выходном слое. Каждый скрытый нейрон влияет на выход множеством путей, и у каждой ошибки — тысячи отцов. Кого винить? И наоборот, кого благодарить за правильный выход? Задача присвоения коэффициентов доверия появляется каждый раз, когда мы пытаемся обучить сложную модель, и представляет собой одну из центральных проблем машинного обучения.

Книга Perceptrons была пронзительно ясной, безупречной с точки зрения математики и оказала катастрофическое воздействие на машинное обучение, которое в те годы ассоциировалось в основном с нейронными сетями. Большинство исследователей (не говоря уже о спонсорах) пришли к выводу, что единственный способ построить интеллектуальную систему — это явно ее запрограммировать, поэтому в науке на 15 лет воцарилась инженерия знаний, а машинное обучение, казалось, было обречено остаться на свалке истории.

Физик делает мозг из стекла

Если об истории машинного обучения снять голливудский блокбастер, Марвин Минский был бы главным злодеем — злой королевой, которая дает Белоснежке отравленное яблоко и бросает ее в лесу (в написанном в 1988 году эссе Сеймур Пейперт даже в шутку сравнивал себя с охотником, которого королева послала в лес убить Белоснежку). Принцем же на белом коне был бы физик из Калифорнийского технологического института по имени Джон Хопфилд. В 1982 году Хопфилд заметил поразительное сходство между мозгом и спиновыми стеклами — экзотическим материалом, который очень любят специалисты по статистической физике. Это открытие привело к возрождению коннекционизма, пиком которого несколько лет спустя стало изобретение первых алгоритмов, способных решать проблему коэффициентов доверия. Кроме того, оно положило начало новой эры, в которой машинное обучение вытеснило инженерию знаний с положения доминирующей парадигмы в науке об искусственном интеллекте.

Спиновые стекла на самом деле не стекла, хотя некоторые стеклоподоб­ные свойства у них есть. Скорее, они магнитные материалы. Каждый электрон — это крохотный магнит, так как у него есть спин, который может указывать «вверх» или «вниз». В таких материалах, как железо, спины электронов обычно выстраиваются в одном направлении: если электрон со спином «вниз» окружен электронами со спином «вверх», он, вероятно, перевернется. Когда большинство спинов в куске железа выстраивается, он превращается в магнит. В обычных магнитах сила взаимодействия между соседними спинами одинакова для всех пар, однако в спиновом стекле она может отличаться и даже бывает негативной, из-за чего расположенные рядом спины принимают противоположные направления. Энергия обычного магнита ниже всего, если все спины выровнены, но в спиновом стекле все не так просто: вообще говоря, нахождение состояния наименьшей энергии для спинового стекла — это NP-полная проблема, то есть к ней можно свести практически любую другую сложную проблему оптимизации. В результате спиновое стекло не обязательно приходит в состояние наименьшей энергии: оно может застрять в локальном, а не глобальном минимуме, то есть состоянии меньшей энергии, чем все состояния, в которые можно из него перейти, поменяв спин. Во многом это похоже на дождевую воду, которая стекает в озеро, а не прямо в океан.

Хопфилд заметил интересное сходство между спиновым стеклом и нейронными сетями. Спин электрона отвечает на поведение своих соседей во многом так же, как нейрон: он переворачивается вверх, если взвешенная сумма соседей превышает пороговое значение, и вниз (или не меняется), если не превышает. Вдохновленный этим фактом, Хопфилд определил тип нейронной сети, которая со временем эволюционирует таким же образом, как спиновое стекло, и постулировал, что состояния минимальной энергии для этой сети — это ее воспоминания. Каждое такое состояние представляет собой «область притяжения» для исходных состояний, которые в нее сходятся, и благодаря этому нейронная сеть способна распознавать паттерны: например, если одно из воспоминаний — черно-белые пиксели, образующие цифру девять, а на изображении — искаженная девятка, сеть сведет ее к «идеальной» цифре и узнает. Внезапно к машинному обучению стало можно применить широкий спектр физических теорий, в эту дисциплину пошел поток статистических физиков, помогая вытащить ее из локального минимума, в котором она застряла.

Однако спиновое стекло — это все еще очень нереалистичная модель мозга. Во-первых, спиновые взаимодействия симметричны, а соединения между нейронами головного мозга — нет. Другой большой проблемой, которую модель Хопфилда игнорировала, было то, что настоящие нейроны действуют по законам статистики: они не детерминистски включаются и выключаются в зависимости от входа, а скорее включаются с большей вероятностью, но не обязательно, при повышении взвешенной суммы входов. В 1985 году исследователи Дэвид Окли, Джеффри Хинтон и Терри Сейновски заменили детерминистские нейроны в сетях Хопфилда вероятностными. Нейронная сеть получила вероятностное распределение по своим состояниям, и состояния высокой энергии стали экспоненциально менее вероятны, чем низкоэнергетические. Вероятность нахождения сети в конкретном состоянии была задана хорошо известным в термодинамике распределением Больцмана, по­этому ученые называли свою сеть машиной Больцмана.

Машина Больцмана состоит из смеси сенсорных и скрытых нейронов (аналогично, например, сетчатке глаза и мозгу) и учится путем попеременного сна и пробуждения, как человек. В разбуженном состоянии сенсорные нейроны срабатывают в соответствии с данными, а скрытые эволюционируют согласно динамике сети и сенсорным входам. Например, если сети показать изображение девятки, нейроны, соответствующие черным пикселям изображения, включатся, другие останутся выключенными, и скрытые нейроны будут произвольно включаться по распределению Больцмана для этих значений пикселей. Во время сна сенсорные и скрытые нейроны свободно блуждают, а перед рассветом нового дня машина сравнивает статистику своих состояний во время сна и во время вчерашней активности и изменяет веса связей так, чтобы согласовать эти состояния. Если в течение дня два нейрона обычно срабатывали вместе, а во сне реже, вес их соединения увеличится. Если наоборот — уменьшится. День за днем предсказанные корреляции между сенсорными нейронами эволюционируют, пока не начнут совпадать с реальными: в этот момент машина Больцмана получает хорошую модель данных, то есть проблема присвоения коэффициентов доверия эффективно решается.

Джефф Хинтон продолжил исследования и в следующие десятилетия перепробовал много вариантов машины Больцмана. Хинтон — психолог, ставший информатиком, и праправнук Джорджа Буля, изоб­ретателя логического исчисления, используемого во всех цифровых компьютерах, — ведущий коннекционист в мире. Он дольше и упорнее других пытался разобраться, как работает мозг. Хинтон рассказывает, что как-то пришел домой с работы и возбужденно крикнул: «Есть! Я понял, как работает мозг!» На что дочь ему ответила: «Папа, опять?!» В последнее время он увлекся глубоким обучением, о котором мы поговорим дальше в этой главе, а также участвовал в разработке метода обратного распространения ошибки — более совершенного, чем машины Больцмана, алгоритма, решающего проблему присвоения кредитов доверия (об этом пойдет речь в следующей главе). Машины Больцмана могут решать эту задачу в принципе, но на практике обучение идет очень медленно и трудно, поэтому такой подход в большинстве случаев нецелесообразен. Для следующего прорыва нужно было отказаться от еще одного чрезмерного упрощения, которое восходит к Маккаллоку и Питтсу.

Самая важная кривая в мире

По отношению к соседям нейрон может быть только в одном из двух состояний — активным и неактивным. Однако здесь не хватает важного нюанса. Потенциалы действия длятся недолго: напряжение подскакивает всего на долю секунды и немедленно возвращается в состояние покоя. Этот скачок едва регистрируется принимающим нейроном: чтобы разбудить клетку, нужна череда скачков с короткими промежутками. Обычные нейроны периодически возбуждаются и без всякой стимуляции. Когда стимуляция накапливается, нейрон возбуждается все чаще и чаще, а затем достигает насыщения — самой высокой частоты скачков напряжения, на которую он способен, после которой увеличение стимуляции не оказывает эффекта. Нейрон больше напоминает не логический вентиль, а преобразователь напряжения в частоту. Кривая зависимости частоты от напряжения выглядит следующим образом:

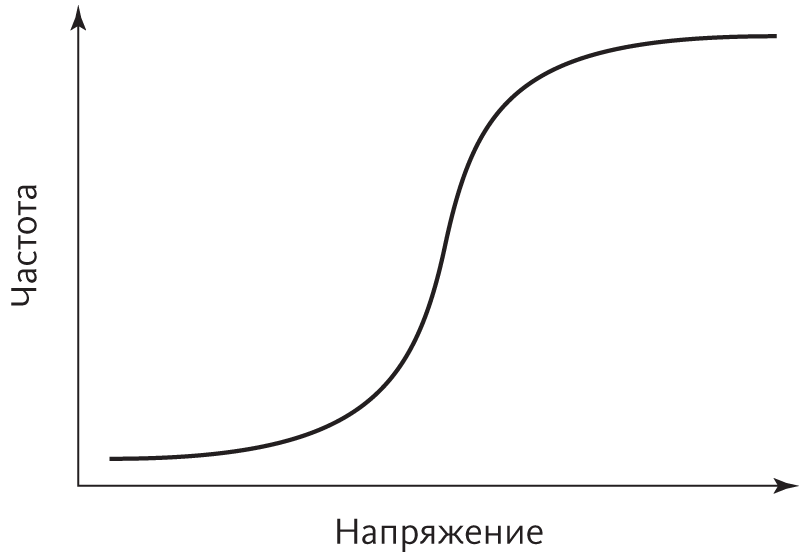
Эту похожую на вытянутую букву S кривую называют по-разному: логисти­ческой, S-образной, сигмоидой. Присмотритесь к ней повнимательнее, потому что это самая важная кривая в мире. Сначала выход медленно растет вместе с входом: так медленно, что кажется постоянным. Затем он начинает меняться быстрее, потом очень быстро, а после все медленнее и медленнее и наконец вновь становится почти постоянным. Кривая транзистора, которая связывает входящее и выходящее напряжение, тоже S-образна, поэтому и компьютеры, и головной мозг наполнены S-кривыми. Но это еще не все. Форму сигмоиды имеют всевозможные фазовые переходы: вероятность, что электрон сменит спин в зависимости от приложенного поля, намагничивание железа, запись бита памяти на твердый диск, открытие ионного канала в клетке, таяние льда, испарение воды, инфляционное расширение молодой Вселенной, прерывистое равновесие в эволюции, смена научных пара­дигм, распространение новых технологий, бегство белого населения из смешанных районов, слухи, эпидемии, революции, падения империй и многое другое. Книгу The Tipping Point: How Little Things Can Make a Big Difference можно было бы (хотя и менее заманчиво) назвать «Сигмоида». Землетрясение — это фазовый переход в относительном положении двух прилегающих тектонических плит, а стук, который мы иногда слышим ночью, — просто сдвиг микроскопических «тектонических плит» в стенах дома, так что не пугайтесь. Йозеф Шумпетер говорил, что экономика развивается трещинами и скачками: творческое разрушение тоже имеет S-образную форму. Финансовые приобретения и потери тоже воздействуют на человеческое счастье по сигмоиде, поэтому не стоит излишне надрываться и переживать. Вероятность, что произвольная логическая формула будет выполнимой — самая суть NP-полных проблем, — следует фазовому переходу от почти единицы к почти нулю по мере увеличения длины формулы. Статистические физики могут изучать фазовые переходы всю жизнь.

В романе Хемингуэя «И восходит солнце» Майка Кэмпбелла спрашивают, как он обанкротился, и тот отвечает: «Двумя способами. Сначала постепенно, а потом сразу». То же самое могли бы сказать в банке Lehman Brothers. В этом суть сигмоиды. Одно из правил прогно­зирования, сформулированных футуристом Полом Саффо, гласит: ищите S-образные кривые. Если не получается «поймать» комфортную температуру в душе — вода сначала слишком холодная, а потом сразу слишком горячая, — вините S-кривую. Развитие по S-образной кривой хорошо видно, когда готовишь воздушную кукурузу: сначала ничего не происходит, затем лопается несколько зерен, потом сразу много, потом почти все взрываются фейерверком, потом еще немного — и можно есть. Движения мышц тоже следуют сигмоиде: медленно, быстро и опять медленно: мультфильмы стали гораздо естественнее, когда диснеевские мультипликаторы поняли это и начали имитировать. По S-кривой движутся глаза, фиксируясь вместе с сознанием то на одном, то на другом предмете. Согласно фазовому переходу меняется настроение. То же самое с рождением, половым созреванием, влюбленностью, браком, беременностью, поступлением на работу и увольнением, переездом в другой город, повышением по службе, выходом на пенсию и смертью. Вселенная — огромная симфония фазовых переходов, от космических до микроскопических, от самых обыденных до меняющих нашу жизнь.

Сигмоида важна не просто как модель. В математике она трудится не покладая рук. Если приблизить ее центральный отрезок, он будет близок прямой. Многие явления, которые мы считаем линейными, на самом деле представляют собой S-образные кривые, потому что ничто не может расти бесконечно. В силу относительности и вопреки Ньютону ускорение не увеличивается линейно с увеличением силы, а следует по сигмоиде, центрированной на нуле. Аналогичная картина наблюдается с зависимостью электрического тока от напряжения в резисторах электрических цепей и в лампочках (пока нить не расплавится, что само по себе очередной фазовый переход). Если посмотреть на S-образную кривую издалека, она будет напоминать ступенчатую функцию, в которой выход в пороговом значении внезапно меняется с нуля до единицы. Поэтому, в зависимости от входящего напряжения, работу транзистора в цифровых компьютерах и аналоговых устройствах, например усилителях и тюнерах, будет описывать та же самая кривая. Начальный отрезок сигмоиды по существу экспоненциальный, а рядом с точкой насыщения она приближается к затуханию по экспоненте. Когда кто-то говорит об экспоненциальном росте, спросите себя: как скоро он перейдет в S-образную кривую? Когда замедлится взрывной рост населения, закон Мура исчерпает свои возможности, а сингулярность так и не наступит? Дифференцируйте сигмоиду, и вы получите гауссову кривую: «медленно — быстро — медленно» превратится в «низко — высоко — низко». Добавьте последовательность ступенчатых S-образных кривых, идущих то вверх, то вниз, и получится что-то близкое к синусоиде. На самом деле каждую функцию можно близко аппроксимировать суммой S-образных кривых: когда функция идет вверх, вы добавляете сигмоиду, когда вниз — отнимаете. Обучение ребенка — это не постепенное улучшение, а накопление S-образных кривых. Это относится и к технологическим изменениям. Взгляните на Нью-Йорк издали, и вы увидите, как вдоль горизонта разворачивается совокупность сигмоид, острых, как углы небоскребов.

Для нас самое главное то, что S-образные кривые ведут к новому решению проблемы коэффициентов доверия. Раз Вселенная — это симфония фазовых переходов, давайте смоделируем ее с помощью фазового перехода. Именно так поступает головной мозг: подстраивает систему фазовых переходов внутри к аналогичной системе снаружи. Итак, давайте заменим ступенчатую функцию перцептрона сигмоидой и посмотрим, что произойдет.

Альпинизм в гиперпространстве

В алгоритме перцептрона сигнал ошибки действует по принципу «все или ничего»: либо правильно, либо неправильно. Негусто, особенно в случае сетей из многих нейронов. Можно понять, что ошибся нейрон на выходе (ой, это была не ваша бабушка?), но как насчет какого-то нейрона в глубинах мозга? И вообще, что значат правота и ошибка для глубинного нейрона? Однако если выход нейрона непрерывный, а не бинарный, картина меняется. Прежде всего мы можем оценить, насколько ошибается выходной нейрон, по разнице между получа­емым и желаемым выходом. Если нейрон должен искрить активностью («Ой, бабушка! Привет!») и он немного активен, это лучше, чем если бы он не срабатывал вовсе. Еще важнее то, что теперь можно распространить эту ошибку на скрытые нейроны: если выходной нейрон должен быть активнее и с ним связан нейрон A, то чем более акти­вен нейрон A, тем больше мы должны усилить соединение между ними. Если A подавляется нейроном B, то B должен быть менее активным и так далее. Благодаря обратной связи от всех нейронов, с которыми он связан, каждый нейрон решает, насколько больше или меньше надо активироваться. Это, а также активность его собственных входных нейронов диктует ему, усиливать или ослаблять соедине­ния с ними. Мне надо быть активнее, а нейрон B меня подавляет? Значит, его вес надо снизить. А нейрон C очень активен, но его соединение со мной слабое? Усилим его. В следующем раунде нейроны-«клиенты», расположенные дальше в сети, подскажут, насколько хорошо я справился с задачей.

Всякий раз, когда «сетчатка» обучающегося алгоритма видит новый образ, сигнал распространяется по всей сети, пока не даст выход. Сравнение полученного выхода с желаемым выдает сигнал ошибки, который затем распространяется обратно через все слои и достигает сетчатки. На основе возвращающегося сигнала и вводных, полученных во время прохождения вперед, каждый нейрон корректирует веса. По мере того как сеть видит все новые и новые изображения вашей бабушки и других людей, веса постепенно сходятся со значениями, которые позволяют отличить одно от другого. Метод обратного распространения ошибки, как называется этот алгоритм, несравнимо мощнее перцептрона. Единичный нейрон может найти только прямую линию, а так называемый многослойный перцептрон — произвольно запутанные границы, при условии что у него есть достаточно скрытых нейронов. Это делает обратное распространение ошибки верховным алгоритмом коннекционистов.

Обратное распространение — частный случай стратегии, очень распространенной в природе и в технологии: если вам надо быстро забраться на гору, выбирайте самый крутой склон, который только найдете. Технический термин для этого явления — «градиентное восхождение» (если вы хотите попасть на вершину) или «градиентный спуск» (если смотреть на долину внизу). Бактерии умеют искать пищу, перемещаясь согласно градиенту концентрации, скажем, глюкозы, и убегать от ядов, двигаясь против их градиента. С помощью градиентного спуска можно оптимизировать массу вещей, от крыльев самолетов до антенных систем. Обратное распространение — эффективный способ такой оптимизации в многослойном перцептроне: продолжайте корректировать веса, чтобы снизить возможность ошибки, и остановитесь, когда станет очевидно, что корректировки ничего не дают. В случае обратного распространения не надо разбираться, как с нуля корректировать вес каждого нейрона (это было бы слишком медленно): это можно делать слой за слоем, настраивая каждый нейрон на основе уже настроенных, с которыми он соединен. Если в чрезвычайной ситуации вам придется выбросить весь инструментарий машинного обучения и спасти что-то одно, вы, вероятно, решите спасти градиентный спуск.

Так как же обратное распространение решает проблему машинного обучения? Может быть, надо просто собрать кучу нейронов, подождать, пока они наколдуют все, что надо, а потом по дороге в банк заехать получить Нобелевскую премию за открытие принципа работы мозга? К сожалению, в жизни все не так просто. Представьте, что у вашей сети только один вес; зависимость ошибки от него показана на этом графике:

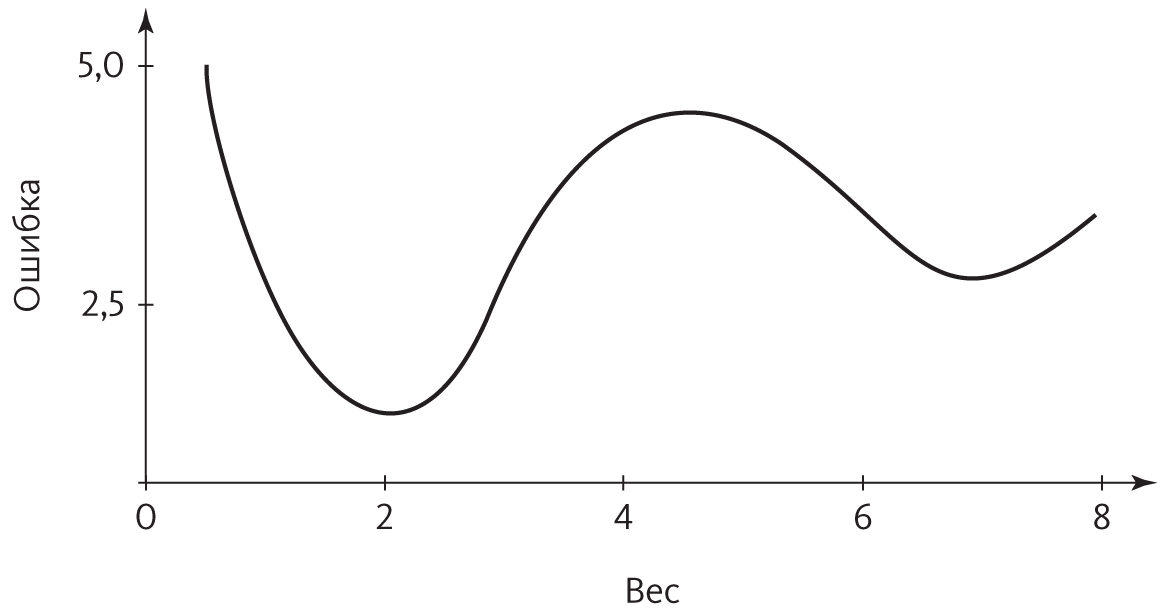
Оптимальный вес, в котором ошибка самая низкая, — это 2,0. Если сеть начнет работу, например, с 0,75, обратное распространение ошибки за несколько шагов придет к оптимуму, как катящийся с горки мячик. Однако если начать с 5,5, мы скатимся к весу 7,0 и застрянем там. Обратное распространение ошибки со своими поэтапными изменениями весов не сможет найти глобальный минимум ошибки, а локальные минимумы могут быть сколь угодно плохими: например, бабушку можно перепутать со шляпой. Если вес всего один, можно перепробовать все возможные значения c шагом 0,01 и таким образом найти оптимум. Но когда весов тысячи, не говоря уже о миллионах или миллиардах, это не вариант, потому что число точек на сетке будет увеличиваться экспоненциально с числом весов. Глобальный минимум окажется скрыт где-то в бездонных глубинах гиперпространства — ищи иголку в стоге сена.

Представьте, что вас похитили, завязали глаза и бросили где-то в Гималаях. Голова раскалывается, с памятью не очень, но вы твердо знаете, что надо забраться на вершину Эвереста. Как быть? Вы делаете шаг вперед и едва не скатываетесь в ущелье. Переведя дух, вы решаете действовать систематичнее и осторожно ощупываете ногой почву вокруг, чтобы определить самую высокую точку. Затем вы робко шагаете к ней, и все повторяется. Понемногу вы забираетесь все выше и выше. Через какое-то время любой шаг начинает вести вниз, и вы останавливаетесь. Это градиентное восхождение. Если бы в Гималаях существовал один Эверест, причем идеальной конической формы, все было бы прекрасно. Но, скорее всего, место, где все шаги ведут вниз, будет все еще очень далеко от вершины: вы просто застрянете на каком-нибудь холме у подножья. Именно это происходит с обратным распространением ошибки, только на горы оно взбирается в гиперпространстве, а не в трехмерном пространстве, как наше. Если ваша сеть состоит из одного нейрона и вы будете шаг за шагом подниматься к наилучшим весам, то придете к вершине. Но в многослойном перцептроне ландшафт очень изрезанный — поди найди высочайший пик.

Отчасти поэтому Минский, Пейперт и другие исследователи не пони­мали, как можно обучать многослойные перцептроны. Они могли представить себе замену ступенчатых функций S-образными кривыми и градиентный спуск, но затем сталкивались с проблемой локальных минимумов ошибки. В то время ученые не доверяли компьютерным симуляциям и требовали математических доказательств работо­способности алгоритма, а для обратного распространения ошибки такого доказательства не было. Но, как мы уже видели, в большинстве случаев локального минимума достаточно. Поверхность ошибки часто похожа на дикобраза: много крутых пиков и впадин, и на самом деле неважно, найдем ли мы самую глубокую, абсолютную впадину — сойдет любая. Еще лучше то, что локальный минимум бывает даже предпочтительнее, потому что он меньше подвержен переобучению, чем глобальный.

Гиперпространство — обоюдоострый меч. С одной стороны, чем больше количество измерений, тем больше места для очень сложных поверхностей и локальных экстремумов. С другой стороны, чтобы застрять в локальном экстремуме, надо застрять во всех измерениях, а во многих одновременно застрять сложнее, чем в трех. В гиперпространстве есть перевалы, проходящие через всю (гипер)местность, поэтому с небольшой помощью со стороны человека обратное распространение ошибки зачастую способно найти путь к идеально хорошему набору весов. Может быть, это не уровень моря, а только легендарная долина Шангри-Ла, но на что жаловаться, если в гиперпространстве миллионы таких долин и к каждой ведут миллиарды перевалов?

Тем не менее придавать слишком большое значение весам, которые находит обратное распространение ошибки, не стоит. Помните, что есть, вероятно, много очень разных, но одинаково хороших вариантов. Обучение многослойного перцептрона хаотично в том смысле, что, начав из слегка отличающихся мест, он может привести к весьма различным решениям. Этот феномен проявляется в случае незначительных отличий как в исходных весах, так и в обучающих данных и имеет место во всех мощных обучающихся алгоритмах, а не только в обратном распространении ошибки.

Мы могли бы избавиться от проблемы локальных экстремумов, убрав наши сигмоиды и позволив каждому нейрону просто выдавать взвешенную сумму своих входов. Поверхность ошибки стала бы в этом случае очень гладкой, и остался бы всего один минимум — глобальный. Дело, однако, в том, что линейная функция линейных функций — по-прежнему линейная функция, поэтому сеть линейных нейронов ничем не лучше, чем единичный нейрон. Линейный мозг, каким бы большим он ни был, будет глупее червяка. S-образные кривые — просто хороший перевалочный пункт между глупостью линейных функций и сложностью ступенчатых функций.

Перцептроны наносят ответный удар

Метод обратного распространения ошибки был изобретен в 1986 году Дэвидом Румельхартом, психологом из Калифорнийского университета в Сан-Диего, в сотрудничестве с Джеффом Хинтоном и Рональдом Уильямсом. Они доказали, кроме всего прочего, что обратное распространение способно справиться с исключающим ИЛИ, и тем самым дали коннекционистам возможность показать язык Минскому и Пейперту. Вспомните пример с кроссовками Nike: подростки и женщины среднего возраста — их наиболее вероятные покупатели. Это можно представить с помощью сети из трех нейронов: один срабатывает, когда видит подростка, другой — женщину среднего возраста, а третий — когда активизируются оба. Благодаря обратному распространению ошибки можно узнать соответствующие веса и получить успешный детектор предполагаемых покупателей Nike. (Вот так-то, Марвин.)

В первых демонстрациях мощи обратного распространения Терри Сейновски и Чарльз Розенберг обучали многослойный перцептрон читать вслух. Их система NETtalk сканировала текст, подбирала фонемы согласно контексту и передавала их в синтезатор речи. NETtalk не только делал правильные обобщения для новых слов, чего не умели системы, основанные на знаниях, но и научился говорить очень похоже на человека. Сейновски любил очаровывать публику на научных мероприятиях, пуская запись обучения NETtalk: сначала лепет, затем что-то более внятное и наконец вполне гладкая речь с отдельными ошибками. (Поищите примеры на YouTube по запросу .)

Первым большим успехом нейронных сетей стало прогнозирование на фондовой бирже. Поскольку сети умеют выявлять маленькие нелинейности в очень зашумленных данных, они приобрели популярность и вытеснили распространенные в финансах линейные модели. Типичный инвестиционный фонд тренирует сети для каждой из многочисленных ценных бумаг, затем позволяет выбрать самые многообещающие, после чего люди-аналитики решают, в какую из них инвестировать. Однако ряд фондов пошел до конца и разрешил алгоритмам машинного обучения осуществлять покупки и продажи самостоятельно. Сколько именно из них преуспело — тайна за семью печатями, но, поскольку специалисты по обучающимся алгоритмам в устрашающем темпе исчезают в недрах хеджевых фондов, вероятно, в этом что-то есть.

Нелинейные модели важны далеко не только на фондовой бирже. Ученые повсеместно используют линейную регрессию, потому что хорошо ее знают, но изучаемые явления чаще нелинейные, и многослойный перцептрон умеет их моделировать. Линейные модели не видят фазовых переходов, а нейронные сети впитывают их как губка.

Другим заметным успехом ранних нейронных сетей стало обучение вождению машины. Беспилотные автомобили впервые привлекли всеобщее внимание на соревнованиях DARPA Grand Challenge в 2004-м и 2005 годах, но за десять с лишним лет до этого ученые Университета Карнеги–Меллон успешно обучили многослойный перцептрон водить машину: узнавать дорогу на видео и поворачивать руль в нужном месте. С небольшой помощью человека — второго пилота — этот автомобиль сумел проехать через все Соединенные Штаты от океана до океана, хотя «зрение» у него было очень мутное (30 × 32 пикселя), а мозг меньше, чем у червяка. (Проект назвали No Hands Across America.) Может быть, это не была первая по-настоящему беспилотная машина, но даже она выгодно отличалась от большинства подростков за рулем.

У метода обратного распространения ошибки несметное количество применений. По мере того как росла его слава, становилось все больше известно о его истории. Оказалось, что, как это часто бывает в науке, метод изобретали несколько раз: французский информатик Ян Лекун и другие ученые наткнулись на него примерно в то же время, что и Румельхарт. Еще в 1980-е годы сообщение о методе обратного распространения отклонили на ведущей конференции по проблемам искусственного интеллекта, потому что, по мнению рецензентов, Минский и Пейперт доказали, что перцептроны не работают. Вообще говоря, Румельхарт считается изобретателем метода скорее по «тесту Колумба»: Колумб не был первым человеком, который открыл Америку, но он был последним. Оказалось, что Пол Вербос, аспирант Гарвардского университета, предложил схожий алгоритм в своей диссертации в 1974 году, а самая большая ирония в том, что Артур Брайсон и Хэ Юци, специалисты по теории управления, добились этого в 1969 году — именно когда Минский и Пейперт публиковали свою книгу Perceptrons! Так что сама история машинного обучения показывает, зачем нам нужны обучающиеся алгоритмы: если бы алгоритмы автоматически выявили, что статьи по теме есть в научной литературе с 1969 года, мы бы не потратили впустую десятилетия, и кто знает, какие открытия были бы сделаны быстрее.

В истории перцептрона много иронии, но печально то, что Фрэнк Розен­блатт так и не увидел второго акта своего творения: он утонул в Чесапикском заливе в том же 1969 году.

Полная модель клетки

Живая клетка — прекрасный пример нелинейной системы. Она выполняет все свои функции благодаря сложной сети химических реакций, превращающих сырье в конечные продукты. Как мы видели в предыдущей главе, структуру этой сети можно открыть символистскими методами, например обратной дедукцией, но для построения полной модели работы клетки нужен количественный подход: надо узнать параметры, которые связывают уровень экспрессии различных генов, соотносят переменные окружающей среды с внутренними переменными и так далее. Это непросто, потому что между этими величинами нет простой линейной зависимости. Свою стабильность клетка скорее поддерживает благодаря пересекающимся петлям обратной связи, и ее поведение очень сложно. Для решения этой проблемы хорошо подходит метод обратного распространения ошибки, который способен эффективно учиться нелинейным функциям. Если бы у нас в руках была полная карта метаболических цепочек и мы располагали достаточными данными наблюдений за всеми соответствующими переменными, обратное распространение теоретически могло бы получить подробную модель клетки и многослойный перцептрон предсказывал бы любую переменную как функцию ее непосредственных причин.

Однако в обозримом будущем у нас будет только частичное понимание клеточного метаболизма и мы сможем наблюдать лишь долю нужных пара­метров. Для получения полезных моделей в условиях недостатка информации и неизбежных противоречий нужны байесовские методы, в которые мы погрузимся в главе 6. То же касается прогнозов для конкретного пациента, если модель уже имеется: байесовский вывод извлечет максимум из неизбежно неполной и зашумленной картины. Хорошо то, что для лечения рака не обязательно понимать функцио­нирование опухолевых клеток полностью и во всех подробностях: достаточно просто обезвредить их, не повреждая нормальные клетки. В главе 6 мы увидим, как правильно сориентировать обучение, обходя то, чего мы не знаем и не обязательно должны знать.

На нынешнем этапе нам известно, что на основе данных и предыдущего знания можно с помощью обратной дедукции сделать вывод о структуре клеточных сетей, однако количество способов его применения порождает комбинаторный взрыв, так что требуется какая-то стратегия. Поскольку мета­болические сети были разработаны эволюцией, возможно, симулирование эволюции в обучающихся алгоритмах как раз подойдет. В следующей главе мы посмотрим, как это сделать.

В глубинах мозга

Когда метод обратного распространения ошибки «пошел в народ», коннекционисты рисовали в воображении быстрое обучение все больших и больших сетей до тех пор, пока, если позволит «железо», они не сравняются с искусственным мозгом. Оказалось, все не так. Обучение сетей с одним скрытым слоем проходило хорошо, но после этого все резко усложнялось. Сети с несколькими слоями работали только в случае, если их тщательно разрабатывали под конкретное применение (скажем, распознавание символов), а за пределами этих рамок метод обратного распространения терпел неудачу. По мере добавления слоев сигнал ошибки расходился все больше и больше, как река, ветвящаяся на мелкие протоки вплоть до отдельных незаметных капелек. Обучение с десятками и сотнями скрытых слоев, как в мозге, оставалось отдаленной мечтой, и к середине 1990-х восторги по пово­ду многослойных перцептронов поутихли. Стойкое ядро коннекционистов не сдавалось, но в целом внимание переместилось в другие области машинного обучения (мы увидим их в главах 6 и 7).

Однако сегодня коннекционизм возрождается. Мы обучаем более глубокие сети, чем когда бы то ни было, и они задают новые стандарты в зрении, распознавании речи, разработке лекарственных средств и других сферах. Новая область — глубокое обучение — появилась даже на первой странице New York Times, но, если заглянуть под капот, мы с удивлением увидим, что там гудит все тот же старый добрый двигатель — метод обратного распространения ошибки. Что изменилось? В общем-то, ничего нового, скажут критики: просто компьютеры сделались быстрее, а данных cтало больше. На это Хинтон и другие ответят: «Вот именно! Мы были совершенно правы!»

По правде говоря, коннекционисты добились больших успехов. Одним из героев последнего взлета на американских горках коннекцио­низма стало непритязательное маленькое устройство под названием автокодировщик — многослойный перцептрон, который на выходе выдает то же, что получил на входе. Он получает изображение вашей бабушки и выдает ту же самую картинку. На первый взгляд это может показаться дурацкой затеей: где вообще можно применить эту штуку? Но вся суть в том, чтобы скрытый слой был намного меньше, чем входной и выходной, то есть чтобы сеть не могла просто научиться копировать вход в скрытый слой, а скрытый слой — в выходной, потому что в таком случае устройство вообще никуда не годится. Однако если скрытый слой маленький, происходит интересная вещь: сеть вынуждена кодировать вход всего несколькими битами, чтобы представить его в скрытом слое, а затем эти биты декодируются обратно до полного размера. Система может, например, научиться кодировать состоящее из миллиона пикселей изображение бабушки всего лишь семью буквами — словом «бабушка» — или каким-то коротким кодом собственного изобретения и одновременно научиться раскодировать это слово в картинку милой вашему сердцу пенсионерки. Таким образом, автокодировщик похож на инструмент для сжатия файлов, но имеет два преимущества: сам разбирается, как надо сжимать, и, как сети Хопфилда, умеет превращать зашумленное, искаженное изображение в хорошее и чистое.

Автокодировщики были известны еще в 1980-х, но тогда их было очень сложно учить, несмотря на всего один скрытый слой. Разобраться, как упаковать большой объем информации в горсть битов, — чертовски сложная проблема (один код для вашей бабушки, немного другой — для дедушки, еще один — для Дженнифер Энистон и так далее): ландшафт гиперпространства слишком изрезан, чтобы забраться на хороший пик, а скрытые элементы должны узнать, из чего складывается избыток исключающих ИЛИ на входе. Из-за этих проблем автокодировщики тогда по-настоящему не привились. Чтобы преодолеть сложности, потребовалось больше десятилетия. Был придуман следующий трюк: скрытый слой надо сделать больше, чем входной и выходной. Что это даст? На самом деле это только половина решения: вторая часть — заставить все, кроме некоторого количества скрытых единиц, быть выключенными в данный момент. Это все еще не позволяет скрытому слою просто копировать вход и, что самое главное, сильно облегчает обучение. Если мы позволим разным битам представлять разные входы, входы перестанут конкурировать за настройку одних и тех же битов. Кроме того, у сети появится намного больше параметров, поэтому у гиперпространства будет намного больше измерений, а следовательно, и способов выбраться из того, что могло бы стать локальными максимумами. Этот изящный трюк называется разреженным автокодировщиком.

Однако по-настоящему глубокого обучения мы пока не видели. Следующая хитрая идея — поставить разреженные автокодировщики друг на друга, как большой сэндвич. Скрытый слой первого становится входом/выходом для второго и так далее. Поскольку нейроны нелинейные, каждый скрытый слой учится более сложным представлениям входа, основываясь на предыдущем. Если имеется большой набор изображений лиц, первый автокодировщик научится кодировать мелкие элементы, например уголки и точки, второй использует это для кодирования черт лица, например кончика носа и радужки глаза, третий займется целыми носами и глазами и так далее. Наконец, верхний слой может быть традиционным перцептроном — он научится узнавать вашу бабушку по чертам высокого уровня, которые дает ниже­лежащий слой. Это намного легче, чем использовать только сырые данные одного скрытого слоя или пытаться провести обратное распространение сразу через все слои. Сеть Google Brain, прорекламированная New York Times, представляет собой бутерброд из девяти слоев автокодировщиков и других ингредиентов, который учится узнавать кошек на видео­роликах на YouTube. На тот момент эта сеть была крупнейшей, которую когда-либо обучали: в ней был миллиард соединений. Неудивительно, что Эндрю Ын, один из руководителей проекта, — горячий сторонник идеи, что человеческий разум сводится к одному алгоритму и достаточно просто его найти. Ын, за обходительными манерами которого скрывается невероятная амбициозность, убежден, что многоярусные разреженные автокодировщики могут привести нас ближе к разгадке искусственного интеллекта, чем все, что мы имели раньше.

Многоярусные автокодировщики — не единственная разновидность глубоких обучающихся алгоритмов. Еще одна основана на машинах Больцмана, встречаются модели зрительной коры на сверточных нейронных сетях. Однако, несмотря на замечательные успехи, все это пока еще очень далеко от головного мозга. Сеть Google умеет распознавать кошачьи мордочки только анфас, а человек узнает кота в любой позе, даже если тот вообще отвернется. Кроме того, сеть Google все еще довольно мелкая: автокодировщики составляют всего три из девяти ее слоев. Многослойный перцептрон — удовлетворительная модель мозжечка — части мозга, ответственной за низкоуровневый контроль движений. Однако кора головного мозга — совсем другое дело. В ней нет, например, обратных связей, необходимых для распространения ошибки, и тем не менее именно в коре происходит настоящее волшебство обучения. В своей книге On Intelligence («Об интеллекте») Джефф Хокинс отстаивает разработку алгоритмов, основанных на близком воспроизведении строения коры головного мозга, но ни один из этих алгоритмов пока не может соперничать с сегодняшними глубокими сетями.

По мере того как мы будем лучше понимать мозг, ситуация может измениться. Вдохновленная проектом «Геном человека», новая дисциплина — коннектомика — стремится составить карту всех мозговых синапсов. В построение полноценной модели Евросоюз вложил миллиарды евро, а американская программа BRAIN, имеющая схожие цели, только в 2014 году получила 100 миллионов долларов финансирования. Тем не менее символисты очень скептически смотрят на этот путь к Верховному алгоритму. Даже если мы будем представлять себе весь мозг на уровне отдельных синапсов, понадобятся (какая ирония) более совершенные алгоритмы машинного обучения, чтобы превратить эту картину в монтажные схемы: о том, чтобы сделать это вручную, не может быть и речи. Хуже то, что, даже получив полную карту головного мозга, мы все еще будем теряться в догадках, как он работает. Нервная система червя Caenorhabditis elegans, состоящая всего из 302 нейронов, была полностью картирована еще в 1986 году, однако мы по-прежнему понимаем ее работу лишь фрагментарно. Чтобы что-то понять в болоте мелких деталей и «выполоть» специфичные для человека подробности и просто причуды эволюции, нужны более высокоуровневые концепции. Мы не строим самолеты путем обратной инженерии птичьих перьев, и самолеты не машут крыльями, однако в основе конструкции самолета лежат принципы аэродинамики, единые для всех летающих объектов. Аналогичных принципов мышления мы все еще не имеем.

Может быть, коннектомика впадает в крайности: некоторые коннекционисты, по слухам, утверждают, что метод обратного распространения и есть Верховный алгоритм: надо просто увеличить масштаб. Но символисты высмеивают эти взгляды и предъявляют длинный перечень того, что люди делать умеют, а нейронные сети — нет. Взять хотя бы «здравый смысл», требующий соединять фрагменты информации, до этого, может быть, никогда и рядом не стоявшие. Ест ли Мария на обед ботинки? Не ест, потому что она человек, люди едят только съедобные вещи, а ботинки несъедоб­ные. Символические системы справляются с этим без проблем — они просто составляют цепочки соответствующих правил, — а многослойные перцептроны этого делать не умеют и, обучившись, будут раз за разом вычислять одну и ту же фиксированную функцию. Нейронные сети — не композиционные, а композиционность — существенный элемент человеческого познания. Еще одна большая проблема в том, что и люди, и символические модели, например наборы правил и деревья решений, способны объяснять ход своих рассуждений, в то время как нейронные сети — большие горы чисел, которые никто не может понять.

Но если у человека есть все эти способности и мозг не выучивает их путем подбора синапсов, откуда они берутся? Вы не верите в волшебство? Тогда ответ — «эволюция». Убежденный критик коннекционизма просто обязан разобраться, откуда эволюция узнала все, что ребенок знает при рождении, — и чем больше мы списываем на врожденные навыки, тем труднее задача. Если получится все это понять и запрограммировать компьютер выполнять такую задачу, будет очень неучтиво отказывать вам в лаврах изобретателя Верховного алгоритма — по крайней мере, одного из его вариантов.

Отправить