ГЛАВА 3

ПРОБЛЕМА ИНДУКЦИИ ЮМА

Вы рационалист или эмпирик?

Рационалисты считают, что чувства обманчивы и единственный верный путь к знанию — логическое рассуждение. Эмпирики уверены, что рассуждения подвержены ошибкам и знание должно быть получено из наблюдений и экспериментов. Французы — рационалисты. Англосаксы (как их называют французы) — эмпирики. Мыслители, юристы и математики — рационалисты. Журналисты, врачи и ученые — эмпирики. «Она написала убийство» — рационалистический криминальный телесериал. «C.S.I.: Место преступления» — эмпирический. В мире информатики теоретики и инже­неры знаний — рационалисты. Хакеры и специалисты по машинному обучению — эмпирики.

Рационалисты любят планировать все заранее, еще до того, как сделают первый шаг. Эмпирики предпочитают пробовать и смотреть, что получится. Не знаю, существует ли ген рационализма или эмпиризма, но, глядя на моих коллег-информатиков, я пришел к выводу, что это почти черты характера: некоторые рационалистичны до мозга костей и не могут быть другими, а другие — насквозь эмпирики и всегда такими были. Представители обоих полюсов могут разговаривать друг с другом и иногда пользоваться полученными другим лагерем результатами, но понимают друг друга лишь отчасти. В глубине души каждый из них верит, что то, чем занимается оппонент, — вторично и не очень интересно.

Рационалисты и эмпирики, наверное, существовали с самого зарождения Homo sapiens. Перед тем как выйти на охоту, Пещерный Бобби долго сидел у костра и размышлял, где его поджидает добыча. Тем временем Пещерная Алиса систематически прочесывала территорию. Поскольку оба вида дошли до наших дней, наверное, будет правильно сказать, что ни один подход не лучше другого. Вы можете подумать, что машинное обучение — это окончательный триумф эмпириков, но скоро мы увидим, что все не так однозначно.

«Рационализм или эмпиризм?» — любимый вопрос философов. Платон был ранним рационалистом, а Аристотель — ранним эмпириком. Но по-настоящему дебаты разгорелись в эпоху Просвещения, когда по каждую сторону встали по три великих мыслителя: Декарт, Спиноза и Лейбниц были ведущими рационалистами; Локк, Беркли и Юм — их соперниками-эмпириками. Доверяя своей силе рассуждения, рационалисты сочиняли теории Вселенной, которые, мягко говоря, не прошли проверку временем, но помимо этого они изобрели фундаментальные математические методики, например математический анализ и аналитическую геометрию. Эмпирики были гораздо практичнее, и их влияние прослеживается везде, начиная с научного метода и заканчивая Конституцией США.

Выдающимся эмпириком и величайшим англоязычным философом всех времен был Дэвид Юм. О его серьезнейшем влиянии говорили такие ученые, как Адам Смит и Чарльз Дарвин, а еще его можно назвать святым покровителем символистов. Юм родился в Шотландии в 1711 году и большую часть своей жизни провел в Эдинбурге, который в XVIII веке процветал и бурлил интеллектуальной жизнью. Юм был человеком добродушным, но при этом строгим скептиком и много времени посвящал разрушению мифов своего времени. Он довел начатые Локком рассуждения об эмпирике до логического завершения и задал вопрос, который с тех пор, как дамоклов меч, висит над любым знанием, от самого банального до самого сложного: как в принципе можно оправдать экстраполяцию того, что мы видели, на то, чего мы не видели? Каждый обучающийся алгоритм в каком-то смысле — попытка ответить на этот вопрос.

Вопрос Юма — отправная точка нашего путешествия. Начнем с того, что проиллюстрируем его примером из повседневной жизни и встретим ее современное воплощение в знаменитой теореме No free lunch — «Бесплатных обедов не бывает». Затем мы посмотрим, что отвечают Юму символисты. Это подведет нас к самой важной проблеме машинного обучения: проблеме переобучения, то есть выделения фантомных закономерностей, которых на самом деле нет. Мы посмотрим, как ее решают символисты и почему машинное обучение — сердце своего рода алхимии, философский камень превращения данных в знания. Для символистов этот камень — само знание. В следующих четырех главах мы увидим решения алхимиков из других «племен».

Быть или не быть свиданию?

У вас есть знакомая девушка, которая вам очень нравится. Вы хотите пригласить ее на свидание, однако вам уже приходилось сталкиваться с отказами, и вы решили задать вопрос, только если будете твердо уверены, что она скажет «да». Пятничным вечером вы сидите с мобильником в руке и пытаетесь решить, звонить или не звонить. Вы помните, что в прошлый раз она не согласилась. Но почему? До этого она два раза сказала «да», потом «нет». Может быть, есть какие-то дни, когда она не хочет никуда ходить? Или, может быть, она любит клубы, а рестораны, напротив, ей не нравятся? Вы человек, необычайно любящий систему, поэтому откладываете телефон в сторону и набрасываете на листке бумаги все, что помните по прошлым встречам.

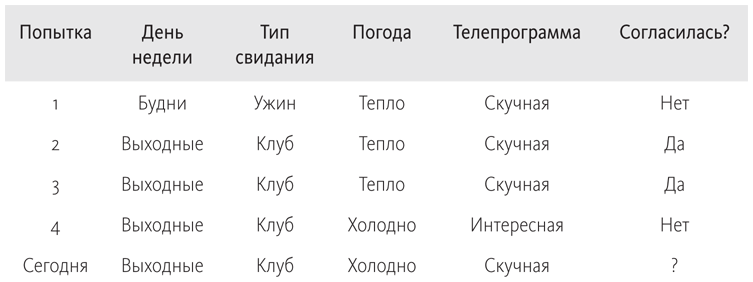
Итак, что вас ждет? Быть свиданию или не быть? Есть ли какая-то законо­мерность во всех этих «да» и «нет»? И самое главное — что эта схема скажет о сегодняшнем дне?

Понятно, что одного фактора для прогнозирования мало. В какие-то выходные она хотела куда-нибудь сходить, а в другие — нет. Иногда ей хотелось развлечься в клубе, а иногда не хотелось и так далее. А как насчет сочетания факторов? Может быть, она любит по выходным ходить в клуб? Нет, не то: случай номер четыре перечеркивает эту догадку. А может быть, она любит гулять только в теплые вечера? В точку! Сработало! В таком случае, учитывая, что на улице морозец, сегодня вечером шансов маловато. Погодите! А что если она любит ходить в клуб, когда по телевизору нет ничего интересного? Это тоже обоснованное предположение, и в таком случае сегодня вас ждет «да»! Быстрее, надо позвонить ей, пока не очень поздно. Стоп. Как узнать, что эта закономерность правильная? Целых два варианта согласуются с вашим прошлым опытом, но они дают противоположные прогнозы. Подумаем еще раз: а если она ходит в клуб только в хорошую погоду? Или она выходит из дома по выходным, когда по телевизору нечего смотреть? Или…

Тут вы в отчаянии комкаете листок бумаги и швыряете его в мусорную корзину. Ничего не получается! Как быть?! Дух Юма печально кивает у вас за плечом. У вас нет никаких оснований предпочесть одно обобщение другому. «Да» и «нет» — одинаково допустимые ответы на вопрос «Что она скажет?». А часы тикают. С горечью вы вытаскиваете из кармана пятак и почти готовы его подбросить.

Вы не одиноки в своем затруднении — оно знакомо и нам. Мы буквально только что отправились в путь навстречу Верховному алгоритму и, похоже, уже наткнулись на непреодолимое препятствие. Есть хоть какой-нибудь способ научиться чему-то на прошлом опыте, чтобы с уверенностью применять знание в будущем? А если такого способа нет, не станет ли машинное обучение безнадежным предприятием? Если уж на то пошло, не построена ли вся наука или даже все человеческое знание на довольно шаткой почве?

Непохоже, чтобы проблему решало увеличение объема данных. Вы можете быть супер-Казановой и встречаться с миллионами женщин, по тысяче раз с каждой, но ваш обширный архив все равно не отве­тит на вопрос, что эта женщина ответит в этот раз. Даже если сегодняшний случай в точности напоминает тот, когда она сказала «да» — тот же день недели, тот же вид свидания, та же погода и те же шоу по телевизору, — это все еще не означает, что она согласится. Вполне может быть, что ее ответ определяется каким-то фактором, о котором вы не подумали или который не можете оценить. Или, может быть, в ее ответах нет ни ладу, ни складу: они случайные, и вы просто ставите себе палки в колеса, пытаясь отыскать в них какую-то схему.

Философы спорили о проблеме индукции Юма с тех самых пор, как он ее сформулировал, но так и не пришли к удовлетворительному ответу. Бертран Рассел любил иллюстрировать эту проблему историей об индюке-индуктивисте. В первое утро индюку дали корм в девять утра. Но он был хорошим индуктивистом и не спешил с выводами. Он много дней собирал наблюдения при всевозможных обстоятельствах, однако его раз за разом кормили в девять утра. Наконец он сделал вывод: да, его всегда будут кормить в девять утра. А потом наступил канун Рождества и ему перерезали горло.

Было бы очень хорошо, если бы проблема Юма была всего лишь философским ребусом, который можно и проигнорировать. Но проигнорировать проблему Юма не получится. Например, бизнес Google основан на угадывании, какие страницы вы ищете, когда вписываете в строку поиска определенные слова. Ключевое преимущество этого поисковика — огромный массив запросов, которые люди вводили в прошлом, и ссылок, на которые они кликали на соответствующих страницах результатов. Но что делать, если кто-то вписывает сочетание ключевых слов, которого нет в архивах? А даже если они и есть, разве можно с уверенностью сказать, что текущий пользователь хочет найти те же страницы, что и все его предшественники?

Как насчет того, чтобы предположить, что будущее будет похоже на прошлое? Это, безусловно, рискованное допущение (у индюка-индуктивиста, например, оно не сработало). С другой стороны, без него знание невозможно, да и жизнь тоже. Мы предпочитаем жить, пусть и без уверенности. К сожалению, даже с таким предположением мы по-прежнему блуждаем в тумане. Оно работает в «тривиальных» случаях: если я врач, а у пациента B точно такие же симптомы, как у пациента A, я предположу, что диагноз будет такой же. Однако если симптомы соответствуют не точно, я по-прежнему ничего не узнаю. Это проблема машинного обучения: обобщение случаев, которые мы еще не видели.

Но, может быть, все не так страшно? Разве с достаточным количеством данных большинство случаев не попадает в категорию «тривиальных»? Нет, не попадает. В предыдущей главе мы уже разобрались, почему запоминание не может быть универсальным обучающимся алгоритмом, но теперь давайте посмотрим на это с количественной точки зрения. Предположим, у вас есть база данных с триллионом записей по тысяче булевых полей в каждой (булево поле — это ответ на вопрос «да или нет»). Это довольно много. Какую долю возможных случаев вы увидели? (Попробуйте угадать, прежде чем читать дальше.) Итак, число возможных ответов — два на каждый вопрос, поэтому для двух вопросов это дважды два (да-да, да-нет, нет-да и нет-нет), для трех вопросов — это два в кубе (2 × 2 × 2 = 2³), а для тысячи вопросов — это два в тысячной степени (2¹⁰⁰⁰). Триллион записей в нашей базе данных — это ничтожно малая доля процента от 2¹⁰⁰⁰, а именно «ноль, запятая, 286 нулей, единица». Итого: неважно, сколько у вас будет данных — тера-, пета-, экса-, зетта- или иоттабайты. Вы вообще ничего не видели. Шансы, что новый случай, который вам нужен для принятия решения, уже есть в базе данных, так исчезающе малы, что без обобщения вы даже не сдвинетесь с места.

Если все это звучит немного абстрактно, представьте, что вы крупный провайдер электронной почты и вам надо пометить каждое входящее письмо как спам или не спам. Даже если у вас есть база данных с триллионом уже помеченных писем, она вас не спасет, потому что шанс, что очередное письмо будет точной копией какого-то из предыдущих, практически равен нулю. У вас нет выбора: надо попытаться более обобщенно определить, чем спам отличается от не-спама. И, согласно Юму, сделать это никак нельзя.

Теорема «Бесплатных обедов не бывает»

Через 250 лет после того, как Юм подбросил нам свою гранату, ей придал элегантную математическую форму Дэвид Уолперт, физик, ставший спе­циалистом по машинному обучению. Его результаты, известные как уже упомянутая выше теорема «Бесплатных обедов не бывает», ставят ограничения на то, как хорош может быть обучающийся алгоритм. Ограничения довольно серьезные: никакой обучающийся алгоритм не может быть лучше случайного угадывания! Вот и приехали: Верховный алгоритм, оказывается, — это просто подбрасывание монетки. Но если серьезно, как может быть, что никакой обучающийся алгоритм не в состоянии победить угадывание с помощью орла или решки? И почему тогда мир полон очень успешных алгоритмов, от спам-фильтров до самоуправляющихся машин (они вот-вот появятся)?

Теорема «Бесплатных обедов не бывает» очень сильно напоминает причину, по которой в свое время Паскаль проиграл бы пари. В своей книге «Мысли», опубликованной в 1669 году, он заявил, что нам надо верить в христианского Бога, потому что, если он существует, это дарует нам вечную жизнь, а если нет — мы мало что теряем. Это был замечательно утонченный аргумент для того времени, но, как заметил на это Дидро, имам может привести точно такой же довод в пользу веры в Аллаха, а если выбрать неправильного бога, придется расплачиваться вечными муками в аду. В целом, учитывая огромное количество мыслимых богов, вы ничего не выиграете, выбрав в качестве объекта своей веры одного из них в пользу любого другого, потому что на любого бога, который говорит «делай то-то», найдется еще один, который потребует нечто противоположное. С тем же успехом можно просто забыть о богах и наслаждаться жизнью без религиозных предрассудков.

Замените «бога» на «обучающийся алгоритм», а «вечную жизнь» — на «точный прогноз», и вы получите теорему «Бесплатных обедов не бывает». Выберите себе любимый алгоритм машинного обучения (мы их много увидим в этой книге), и на каждый мир, где он справляется лучше случайного угадывания, я, адвокат дьявола, коварно создам другой мир, где он справляется ровно настолько же хуже: все, что мне надо сделать, — перевернуть ярлыки на всех случаях, которых вы не видели. Поскольку ярлыки на увиденных случаях совпадают, ваш обучающийся алгоритм никак не сможет различить мир и антимир, и в среднем из двух случаев он будет так же хорош, как случайное угадывание. Следовательно, если совместить все возможные миры с их антимирами, в среднем ваш обучающийся алгоритм будет равен подбрасыванию монетки.

Однако не торопитесь сдаваться и списывать со счетов машинное обучение и Верховный алгоритм. Дело в том, что нас заботят не все возможные миры, а только тот, в котором живем мы с вами. Если мы уже знаем что-то об этом мире и введем это в наш обучающийся алгоритм, у него появится преимущество перед произвольным угадыванием. На это Юм ответил бы, что знание как таковое тоже должно быть получено путем логической индукции и, следовательно, ненадежно. Это верно, даже если знание закодировано в наш мозг эволюцией. Однако нам приходится идти на этот риск. Еще можно задуматься: есть ли бесспорный, фундаментальный самородок знаний, на котором можно построить всю свою индукцию? (Что-то вроде Декартова «Я мыслю, следовательно, я существую», хотя сложно придумать, как превратить конкретно это утверждение в обучающийся алгоритм.) Я думаю, ответ — «да, есть», и мы увидим этот самородок в главе 9.

Практическое следствие теоремы «Бесплатных обедов не бывает» — то, что обучение без знаний невозможно. Одних данных недостаточно. Если начинать с чистого листа, мы придем к чистому листу. Машинное обучение — своего рода насос знаний. С помощью машинного обучения можно «выкачать» из данных много знаний, но сначала нам надо его заполнить данными, как насос перед пуском заполняют водой.

Машинное обучение с точки зрения математики относится к категории некорректно поставленных задач, так как единственного решения не существует. Вот простой пример: сумма каких двух чисел равна 1000? Если исходить из того, что числа положительные, у этой задачи 500 возможных ответов: 1 и 999, 2 и 998 и так далее. Чтобы решить некорректно поставленную задачу, придется ввести дополнительные условия. Если я скажу, что второе число в три раза больше первого, — все станет просто! Ответ — 250 и 750.

Том Митчелл, ведущий символист, называет это «тщетностью беспристрастного обучения». В обычной жизни слово «пристрастный» имеет негативный оттенок: предвзятость суждений — это плохо. Однако в машинном обучении предвзятые суждения необходимы. Без них нельзя учиться. На самом деле они незаменимы и для человеческого познания, но при этом так жестко встроены в наш мозг, что мы принимаем их как должное. Вопросы вызывает только пристрастность, выходящая за эти рамки.

Аристотель говорил, что в разуме нет ничего такого, чего не было бы в органах чувств. Лейбниц добавил: «Кроме самого разума». Челове­ческий мозг — это не tabula rasa, потому что это совсем не доска: доска пассивна, на ней пишут, а мозг активно обрабатывает получаемую информацию. Доска, на которой он пишет, — это память, и она и впрямь сначала чиста. С другой стороны, компьютер — действительно чистая доска, до тех пор пока его не запрограммируют: активный процесс надо заложить в память, прежде чем что-нибудь произойдет. Наша цель — найти простейшую программу, какую мы только можем написать, чтобы она продолжала писать саму себя путем неограниченного чтения данных, пока не узнает все, что можно узнать.

У машинного обучения имеется неотъемлемый элемент азартной игры. В конце первого фильма про Грязного Гарри Клинт Иствуд гонится за ограбившим банк бандитом и раз за разом в него стреляет. Наконец грабитель повержен. Он лежит рядом с заряженным ружьем и не знает, хватать его или нет. Было шесть выстрелов или только пять? Гарри сочувствует (если можно так выразиться): «Тебе надо лишь спросить: “Повезет или нет?” Ну как, мерзавец?» Этот вопрос специалисты по машинному обучению должны задавать себе каждый день, когда они приходят на работу. Повезет или нет? Как и эволюция, машинное обучение не будет каждый раз попадать в десятку. Вообще говоря, ошибки — не исключение, а правило. Но это нормально, потому что промахи мы отбрасываем, а попаданиями пользуемся, и важен именно совокупный результат. Когда мы получаем новую частицу знаний, она становится основой для логической индукции еще большего знания. Единственный вопрос — с чего начать.

Подготовка насоса знаний

В «Математических началах натуральной философии» наряду с законами движения Ньютон формулирует четыре правила индукции. Они далеко не так известны, как физические законы, но, пожалуй, не менее важны. Ключевое правило — третье, которое можно перефразировать так:

Принцип Ньютона: то, что верно для всего, что мы видели, верно для всего во Вселенной.

Не будет преувеличением сказать, что это невинное вроде бы утвержде­ние — сердце ньютоновской революции и современной науки. Законы Кеплера применялись ровно к шести сущностям — планетам Солнечной системы, которые в то время были известны. Законы Ньютона применимы ко всем до единой частицам материи во Вселенной. Прыжок в обобщении между этими законами просто колоссальный, и это прямое следствие сформулированного Ньютоном правила. Приведенный выше принцип сам по себе — насос знаний невероятной мощи. Без него не было бы законов природы, а только вечно неполные заплатки из небольших закономерностей.

Принцип Ньютона — первое неписаное правило машинного обучения. Путем индукции мы выводим самые широко применимые законы, какие только возможно, и сужаем их действие, только если данные вынуждают нас это сделать. На первый взгляд это может показаться чрезмерной, даже нелепой самоуверенностью, но в науке такой подход работает уже более трех сотен лет. Безусловно, можно представить вселенную настолько разно­родную и капризную, что Ньютонов принцип будет систематически терпеть поражение, но наша Вселенная не такая.

Тем не менее принцип Ньютона лишь первый шаг. Нам все еще надо найти истину во всем том, что мы увидели: извлечь закономерности из сырых данных. Стандартное решение: предположить, что форму истины мы знаем, а работа алгоритма машинного обучения — это облечь ее в плоть. Например, в описанной выше проблеме со свиданием можно предположить, что ответ девушки будет определяться чем-то одним. В таком случае обучение заключается просто в рассмотрении всех известных факторов (день недели, тип свидания, погода, телепрограмма) и проверке, всегда ли корректно они предопределяют ответ. Сложность в том, что ни один фактор не подходит! Вы рискнули и проиграли, по­этому немного ослабляете условия. Что если ответ девушки определяется сочетанием двух факторов? Четыре фактора по два возможных значения для каждого — это 24 варианта для проверки (шесть пар факторов, из которых можно выбирать, умноженные на два варианта для каждого значения фактора). Теперь у нас глаза разбегаются: целых четыре сочетания двух факторов корректно предсказывают результат! Что делать? Если вы чувствуете удачу, можете выбрать какой-то из них и надеяться на лучшее. Однако более разумный подход — демократический: дайте им «проголосовать» и выберите победивший прогноз.

Если все сочетания двух факторов проигрышные, можно попробовать все сочетания любого числа факторов. Специалисты по машинному обучению и психологи называют это «конъюнктивными понятиями». К таким понятиям относятся словарные определения: «У стула есть сиденье, и спинка, и некоторое число ножек». Уберите любое из этих условий, и это уже будет не стул. Конъюнктивное понятие можно найти у Толстого в первой строке «Анны Карениной»: «Все счастливые семьи похожи друг на друга, каждая несчастливая семья несчастлива по-своему». То же верно и для отдельных людей. Чтобы быть счастливым, нужны здоровье, любовь, друзья, деньги, любимая работа и так далее. Уберите что-то из этого списка, и человек будет несчастлив.

В машинном обучении примеры концепции называют положительными примерами, а контрпримеры — отрицательными. Если вы пытаетесь научиться узнавать кошек на картинке, изображения кошек будут положительными примерами, а собак — отрицательными. Если составить базу данных семей из мировой литературы, Каренины будут отрицательным примером счастливой семьи, но найдется и некоторое количество драгоценных положительных примеров.

Для машинного обучения типично начинать с ограничивающих условий и постепенно ослаблять их, если они не объясняют данных. Этот процесс обычно выполняется обучающимся алгоритмом автоматически, без какой-либо помощи со стороны человека. Сначала алгоритм тестирует все отдельные факторы, затем все сочетания двух факторов, потом все сочетания трех и так далее. Однако здесь мы опять сталкиваемся с проблемой: конъюнктивных понятий очень много, а времени, чтобы все перепробовать, недостаточно.

Описанный выше случай со свиданиями несколько обманчив, потому что содержит всего четыре переменных и четыре примера. Поэтому представьте, что вы управляете сайтом знакомств и вам надо разобраться, какие пары познакомить друг с другом. Если каждый пользователь заполнит анкету из 50 вопросов с ответами «да» или «нет», у каждой потенциальной пары будет сотня атрибутов, по 50 на каждого человека. Можно ли дать конъ­юнктивное определение понятия «подходящая пара» на основе информации о парах, которые сходили на свидание и сообщили о результатах? Для этого пришлось бы перепробовать 3¹⁰⁰ возможных определений (три варианта для каждого атрибута: «да», «нет» и «не входит в концепцию»). Даже если в вашем распоряжении самый быстрый в мире компьютер, к моменту, когда он закончит, все пары уже давно умрут, а вы разоритесь, если только вам не повезет и в точку не попадет очень короткое определение. Правил много, времени мало. Надо придумать что-то получше.

Вот один из выходов. Предположите на секунду, пусть это и невероятно, что все пары подходят друг другу. Затем попробуйте исключить все пары, которые не удовлетворяют единственному атрибуту определения. Повторите это для всех атрибутов и выберите тот, который исключит больше всего плохих пар и меньше всего хороших. Ваше определение теперь будет выглядеть, например, так: «Они подходят друг другу, только если он открытый человек». Теперь попробуйте прибавить к этому определению каждый из оставшихся атрибутов и выберите тот, что исключит больше всего оставшихся плохих пар и меньше всего хороших. Возможно, определение станет таким: «Они подходят друг другу, только если оба — открытые люди». Попробуйте прибавить к найденным чертам третий атрибут и так далее. Когда вы исключите все плохие пары — готово: у вас в руках определение концепции, которое включает все положительные примеры и исключает все отрицательные. Например: «Они хорошая пара, если оба — открытые люди, он любит собак, а она не любительница кошек». Теперь можно выбросить все данные и оставить только это определение, потому что оно включает все, что важно для ваших задач. К этому алгоритму вы гарантированно придете в разумные сроки, а еще это первый настоящий обучающийся алгоритм, с которым мы познакомились в этой книге!

Как править миром

Тем не менее на конъюнктивных понятиях далеко не уедешь. Проблема, как выразился Редьярд Киплинг, в том, что «путей в искусстве есть семь и десять раз по шесть, и любой из них для песни — лучше всех». В реальной жизни понятия дизъюнктивны. У стульев может быть и четыре ножки, и одна, а иногда они вообще без ножек. В шахматы можно выиграть бесчисленным количеством способов. Электронные письма со словом «виагра», скорее всего, спам, но то же самое можно сказать о письмах со словом «БЕСПЛАТНО!!!». Кроме того, у всех правил бывают исключения. Некоторые неблагополучные семьи умудряются быть счастливыми. Все птицы летают, только если это не пингвины, страусы, казуары и киви (а также если у них не сломано крыло, они не сидят в клетке и так далее).

Так что нам нужно находить концепции, которые заданы целым набором правил, а не одним, например:

Если вам нравятся IV—VI эпизоды «Звездных войн», значит, вам понравится «Аватар».

Если вам нравятся «Звездный путь: Следующее поколение» и «Титаник», вам понравится «Аватар».

Если вы член экологической организации Sierra Club и любите научную фантастику, вам понравится «Аватар».

Или:

Если вашей кредитной карточкой вчера пользовались в Китае, Канаде и Нигерии, значит, ее украли.

Если вашей кредитной карточкой пользовались два раза после 11 вечера в будний день, значит, ее украли.

Если с вашей кредитной карточки купили бензин на один доллар, значит, ее украли.

(Если вы не поняли последнее правило, небольшое пояснение: раньше воры обычно покупали бензин на доллар, чтобы убедиться, что украденная карточка работает. Потом специалисты по добыче данных раскусили этот прием.)

С помощью алгоритма для нахождения конъюнктивных понятий, с кото­рым мы познакомились выше, можно составлять подобные наборы по одному правило за правилом. Когда мы нашли правило, можно отбросить положительные примеры, которые оно включает, поэтому следующее правило будет пытаться охватить как можно больше оставшихся положительных примеров и так далее, пока все не будет включено. Это применение принципа «разделяй и властвуй», древнейшей стратегии в научном арсенале. Кроме того, мы можем улучшить алгоритм поиска отдельных правил, если будем иметь в запасе не одну, а n гипотез и на каждом этапе расширять их всеми возможными способами, сохраняя n лучших результатов.

Открытием такого способа поиска правил мы обязаны польскому информатику Рышарду Михальскому. Его родной город Калуш в разное время входил в состав Польши, СССР, Германии и Украины, и, возможно, именно это повлияло на его склонность к дизъюнктивным понятиям. Эмигрировав в 1970 году в США, он вместе с Томом Митчеллом и Джейми Карбонеллом основал символистскую школу машинного обучения. У Михальского был весьма деспотичный характер. Выступавшие на конференциях по машинному обучению не были застрахованы от того, что в конце он не поднимет руку и не заявит, что только что услышал повторение одной из своих старых идей.

Наборы правил популярны в торговых сетях: с их помощью определяют, какие товары надо закупать. Как правило, ретейлеры используют более всесторонний подход, чем «разделяй и властвуй», и ищут все правила, которые с большой вероятностью прогнозируют спрос. Пионер в этой области — Walmart. Еще на заре применения этого метода они открыли, что с подгузниками часто покупают пиво. Звучит странно? Одна из интерпретаций такая: молодые матери посылают мужей в супер­маркет за подгузниками, а те в качестве компенсации за моральный ущерб покупают себе ящик пива. Зная это, супермаркеты теперь могут продавать больше пенного напитка, выставляя его на полках по соседству с подгузниками. К такому выводу никогда не придешь без поиска правил: «закон пива и подгузников» стал легендой среди специалистов по добыче данных (некоторые, правда, утверждают, что это скорее городская легенда). Как бы то ни было, все это довольно далеко от проб­лем разработки цифровых схем, которые были на уме у Михальского, когда он в 1960-х впервые начал задумываться о логическом поиске правил. Изобретая новый алгоритм машинного обучения, нельзя даже представить себе все области, в которых он может найти применение.

Первый практический урок в области обучения правилам я получил, когда только переехал в США, чтобы поступить в аспирантуру, и подал заявку на получение кредитной карточки. Банк прислал мне письмо, в котором говорилось: «К сожалению, ваше заявление отклонено по следующим причинам: НЕДОСТАТОЧНО ДОЛГОЕ ПРОЖИВАНИЕ ПО ТЕКУЩЕМУ АДРЕСУ И ОТСУТСТВИЕ КРЕДИТНОЙ ИСТОРИИ» (или еще что-то в том же духе заглавными буквами). Тогда я понял, что в области машинного обучения предстоит еще немало работы.

Между слепотой и галлюцинациями

Наборы правил намного мощнее, чем конъюнктивные понятия. Вообще говоря, они настолько сильны, что с их помощью можно выразить любое понятие. Почему — понять несложно: если вы дадите мне полный список всех примеров какого-то понятия, я могу просто превратить каждый из них в правило, которое описывает все его атрибуты, и набор таких правил станет определением понятия. Если вернуться к нашей проблеме свидания, одним из правил будет такое: Если сегодня выходной, на улице тепло, по телевизору не показывают ничего хорошего и я предложу сходить в клуб, она скажет «да». В таб­лице содержится лишь несколько примеров, но, если в нее внести все 2 × 2 × 2 × 2 = 16 возможных и каждому присвоить ярлык «Есть свидание» или «Нет свидания», превращение каждого положительного примера в правило решит проблему.

Наборы правил — мощный, но обоюдоострый меч. Их достоинство в том, что всегда можно найти набор правил, который идеально подойдет к имеющимся данным. Однако не спешите радоваться, что поймали удачу за хвост. Не забывайте: есть серьезнейший риск столкнуться с совершенно бессмысленным правилом. Помните теорему о бесплатных обедах? Учиться без знаний нельзя. Предположение, что понятие можно определить набором правил, — пустое предположение.

Один из частных случаев бесполезного набора правил просто включает все положительные примеры, которые вы видели, и ничего больше. Он может показаться стопроцентно точным, но это иллюзия: по его предсказаниям, каждый новый пример будет отрицательным, поэтому на каждом положительном он будет ошибаться. Если в целом положительных примеров больше, чем отрицательных, получится даже хуже, чем подбрасывать монетку. Представьте себе фильтр, который будет отправлять письма в спам, только если они точная копия сообщения, ранее помеченного как спам. Научить этому легко, это здорово работает с уже помеченной выборкой, но с тем же успехом можно вообще не иметь спам-фильтра. К сожалению, наш алгоритм «разделяй и властвуй» легко может научиться набору правил вроде этого.

В рассказе «Фунес памятливый» Хорхе Луис Борхес повествует о встрече с молодым человеком с идеальной памятью. Сначала такой дар может показаться редким везением, но на самом деле это ужасное проклятье. Фунес может вспомнить точную форму туч в небе в произвольный момент времени в прошлом, но ему сложно понять, что собака, которую он видел сбоку в 15:14, — та же самая собака, которую он видел спереди в 15:15, и он каждый раз удивляется собственному отражению в зеркале. Фунес неспособен обобщать, поэтому для него две вещи одинаковы, только если они выглядят идентично, вплоть до мелочей. Неограниченное обучение правилам похоже на Фунеса и совершенно неработоспособно. Учиться — значит забывать о подробностях в той же степени, как помнить о важных элементах. Компьютеры — высшее проявление синдрома саванта: они без малейших проблем запоминают все, но хотим мы от них не этого.

Проблема не ограничивается массовым запоминанием частностей. Каждый раз, когда обучающийся алгоритм находит в данных законо­мерность, которая в реальном мире ошибочна, мы говорим, что он «подо­гнал под ответ». Переобучение — центральная проблема машинного обучения: ей посвящено больше статей, чем любой другой теме. Каждый мощный обучающийся алгоритм — символистов, коннекционистов или любой другой — должен беспокоиться о паттернах-галлюцинациях, и единственный безопасный способ их избежать — серьезно ограничить то, чему обучающийся алгоритм может научиться: например, требовать, чтобы это были короткие конъюнктивные понятия. К сожалению, с водой можно выплеснуть и ребенка, и тогда алгоритм машинного обучения будет неспособен увидеть в данных большинство истинных схем. Таким образом, хороший обучающийся алго­ритм всегда станет балансировать на узкой тропинке между слепотой и галлюцинациями.

Люди тоже не застрахованы от переобучения. Можно даже сказать, что это корень многих наших бед. Представьте себе ситуацию: маленькая белая девочка видит в торговом центре девочку-мексиканку и кричит: «Мама, смотри, ребенок-служанка!» (это реальный случай). Дело не в прирожденном расизме. Скорее, она слишком обобщила представление о тех немногих латиноамериканках, которых успела увидеть за свою короткую пока жизнь, — в мире полно представительниц этой этнической группы, не работающих прислугой, но девочка их пока не встретила. Наши убеждения основаны на опыте, а опыт дает очень неполную картину мира, поэтому перепрыгнуть к ложным выводам несложно. Ум и эрудиция тоже не панацея. Именно переобучением было утверждение Аристотеля, что для того, чтобы объект продолжал двигаться, к нему должна быть приложена сила. Лишь гениаль­ный Галилей интуитивно почувствовал, что невозмущенные тела тоже продолжают двигаться, хотя не был в открытом космосе и собственными глазами этого не видел.

Однако обучающиеся алгоритмы, с их почти неограниченной способностью находить закономерности в данных, особенно уязвимы для переобучения. За время, пока человек будет искать одну закономерность, компьютер найдет миллионы. В машинном обучении величайшая сила компьютера — способность обрабатывать огромное количество данных и бесконечно, без устали повторять одно и то же — одновременно становится его ахиллесовой пятой. Просто удивительно, сколько всего можно найти, если хорошенько поискать. В бестселлере 1998 года The Bible Code утверждается, что Библия содержит предсказания будущих событий, которые можно прочитать, если брать буквы через определенные интервалы и составлять из них слова. К сожалению, есть столько способов это сделать, что «предсказания» обязательно найдутся в любом достаточно длинном тексте. Скептики ответили автору пророчествами из «Моби Дика» и постановлений Верховного суда, а также нашли в Книге Бытия упоминания о Розуэлле и летающих тарелках. Джон фон Нейман, один из основоположников информатики, как-то точно заметил: «С четырьмя параметрами я могу подогнать слона, а с пятью заставлю его махать хоботом». Сегодня мы каждый день учим модели с миллионами параметров. Этого достаточно, чтобы каждый слон в мире махал хоботом по-своему. Кто-то даже сказал, что «добывать данные — значит пытать их до тех пор, пока они не признаются».

Переобучение серьезно усугубляется шумом. Шум в машинном обучении означает просто ошибки в данных или случайные события, которые нельзя предвидеть. Представьте, что ваша знакомая, которую вы собираетесь пригласить на свидание, очень любит ходить по клубам, когда по телевизору нет ничего интересного, но вы неправильно запомнили случай номер три и записали, что в тот вечер по телевидению показывали что-то хорошее. Если теперь вы попытаетесь составить набор правил, который делает исключение для того вечера, результат, вероятно, будет хуже, чем если просто его проигнорировать. Или пред­ставьте, что у девушки было похмелье после предыдущего вечера и она сказала «нет», хотя при обычных обстоятельствах согласилась бы. Если вы не знаете о ее состоянии, обучение набору правил, который верно учитывает этот пример, будет контрпродуктивным: целе­сообразнее «неправильно классифицировать» его как «нет». Все очень плохо: шум может сделать невозможным составление любого связного набора правил. Обратите внимание, что случаи два и три на самом деле неразличимы: у них точно такие же атрибуты. Если ваша знакомая сказала «да» во втором случае и «нет» в третьем, отсутствует правило, которое верно учло бы оба.

Переобучение возникает, когда у вас слишком много гипотез и недостаточно данных, чтобы их различить. Проблема в том, что даже в простых конъюнктивных обучающихся алгоритмах число гипотез растет экспоненциально с числом атрибутов. Экспоненциальный рост — страшная сила. Бактерия E. coli может делиться надвое примерно каждые 15 минут. Если бы у нее было достаточно питательных веществ, она бы за день разрослась в бактериальную массу размером с нашу планету. Когда количество элементов, необходимых алгоритму для работы, растет в геометрической прогрессии с увеличением размера вводных данных, информатики называют это комбинаторным взрывом и бегут в укрытие. В машинном обучении количество возможных частных случаев какого-либо понятия — экспоненциальная функция числа атрибутов: если атрибуты булевы, с каждым новым атрибутом число возможных частных случаев удваивается, каждый случай расширяется для «да» или «нет» этого атрибута. В свою очередь, число возможных понятий — это экспоненциальная функция числа возможных частных случаев: поскольку понятие отмечает каждый случай как положительный или отрицательный, добавление частного случая удваивает число возможных понятий. В результате число понятий — это экспоненциальная функция экспоненциальной функции числа атрибутов! Другими словами, машинное обучение — комбинаторный взрыв комбинаторных взрывов. Может, лучше просто сдаться и не тратить времени на такую безнадежную проблему?

К счастью, при обучении получается «отрубить голову» одной из экспо­нент и оставить только «обычную» единичную неразрешимую экспоненциальную проблему. Представьте, что у вас полная сумка листочков с определениями понятий и вы достаете наугад одно из них, чтобы посмотреть, насколько хорошо оно подходит к данным. Вероятность, что плохое определение подойдет всей тысяче примеров в ваших данных, не больше, чем ситуация, когда монетка тысячу раз подряд падает орлом вверх. «У стула четыре ноги, и он красный, либо у него есть сиденье, но нет ножек», вероятно, подойдет к некоторым, но не ко всем стульям, которые вы видели, а также подойдет к некоторым, но не ко всем другим предметам. Поэтому, если случайное определение корректно подходит к тысяче примеров, крайне маловероятно, что оно неправильное. По крайней мере, оно достаточно близко к истине. А если определение согласуется с миллионом примеров, оно практически наверняка верно, иначе почему оно подходит ко всем этим примерам?

Конечно, реальный алгоритм машинного обучения не просто берет из мешка одно произвольное определение: он пробует их целую охапку, и отбор не происходит произвольным образом. Чем больше определений пробует алгоритм, тем больше вероятность, что одно из них подойдет ко всем примерам хотя бы случайно. Если сделать миллион повторений по тысяче бросков монетки, практически наверняка хотя бы одно повторение даст все орлы, а миллион — это достаточно скромное число гипотез для рассмотрения: оно примерно соответствует числу возможных конъюнктивных понятий, если у примеров всего 13 атрибутов. (Обратите внимание, что вам не надо явно пробовать понятия одно за другим. Если лучшие, которые вы нашли с использованием конъюнктивного обучающегося алгоритма, подходят ко всем примерам, результат будет тот же самый.)

Итого: обучение — гонка между количеством данных, имеющихся в вашем распоряжении, и количеством рассматриваемых вами гипотез. Увеличение объема данных экспоненциально уменьшает количество прошедших про­верку гипотез, но, если гипотез изначально много, в конце все равно может остаться некоторое количество плохих. Есть золотое правило: если обучающийся алгоритм учитывает только экспоненциальное число гипотез (например, все возможные конъюнктивные понятия), то экспоненциальный выигрыш от данных решает проблему, и все в порядке, при условии, что у вас множество примеров и не очень много атрибутов. С другой стороны, если алгоритм рассматривает дважды экспоненциальное число (например, все возможные наборы правил), тогда данные отменяют только одну из экспонент, и трудности остаются. Можно даже заранее решить, сколько примеров понадобится, чтобы быть достаточно уверенным, что выбранная обучающимся алгоритмом гипотеза очень близка к истинной, при условии, что к ней подходят все данные. Другими словами, чтобы гипотеза была, вероятно, приблизительно правильной. За изобретение этого типа анализа гарвардский ученый Лесли Вэлиант получил премию Тьюринга — Нобелевскую премию по информатике. Его книга на эту тему называется Probably Approximately Correct («Возможно, приблизительно верно»).

Точность, которой можно доверять

На практике анализ по Вэлианту обычно дает очень пессимистичные результаты и требует больше данных, чем есть в наличии. Как же решить, верить ли обучающемуся алгоритму? Все просто: не верьте, пока не проверите результаты на данных, которые обучающийся алгоритм не видел. Если схемы, выдвинутые им в качестве гипотезы, окажутся верны и для новых данных, можно быть уверенным, что они реальные. В противном случае вы будете знать, что имело место переобучение. Это просто применение научного метода к машинному обучению: новой теории мало объяснить прошлый опыт (такую состряпать несложно) — она должна также делать новые предсказания, а принимают ее только после того, как предсказания были экспериментально подтверждены. (И даже тогда лишь предварительно, потому что будущие данные по-прежнему могут ее фальсифицировать.)

Общая теория относительности Эйнштейна стала общепринятой, только когда Артур Эддингтон эмпирически подтвердил, что Солнце отклоняет свет далеких звезд. Но вам не надо ждать, пока поступят новые данные, чтобы решить, можно ли доверять алгоритму машинного обучения. Лучше взять все данные, которые у вас есть, и произвольно разделить их на обучающее множество, которое вы дадите алгоритму, и тестовое множество, которое надо cпрятать от него и использовать для верификации точности. Точность на скрытых данных — золотой стандарт в машинном обучении. Можно написать статью о том, какой прекрасный новый обучающийся алгоритм вы придумали, но, если на скрытых данных он значительно не превосходит уже имеющиеся, статью никто не опубликует.

Точность на данных, которые алгоритм еще не видел, — настолько строгий критерий, что многие научные теории его не проходят. От этого они не становятся бесполезными, ведь наука — это не только предсказания, но и объяснение и понимание, однако в итоге, если модели не делают точных прогнозов на новых данных, нельзя быть уверенным, что лежащие в основе явления по-настоящему поняты и объяснены. А для машинного обучения тестирование на скрытых данных незаменимо, потому что это единственный способ определить, случилось ли с обучающимся алгоритмом переобучение.

Но и точность на тестовой выборке не гарантия от ошибок. Согласно легенде, один из ранних простых обучающихся алгоритмов со стопроцентной точностью отличал танки и в обучающей, и в тестовой выборке, каждая из которых состояла из 100 изображений. Удивительно или подозрительно? Оказалось, что все картинки с танками были светлее, и это все, что увидел обучающийся алгоритм. В наши дни выборки данных крупнее, но качество сбора данных не обязательно лучше, по­этому нельзя терять бдительность. Реалистичная эмпирическая оценка сыграла важную роль в превращении машинного обучения из молодой дисциплины в зрелую науку. До конца 1980-х исследователи каждого из «племен» в основном верили собственным аргументам, исходили из того, что их парадигма фундаментально лучше, и мало общались с другими лагерями. Затем символисты, например Рэй Муни и Джуд Шавлик, начали систематически сравнивать разные алгоритмы на тех же наборах данных, и — вот сюрприз! — оказалось, что однозначного победителя нет. Сегодня соперничество продолжается, но перекрестное опыление встречается гораздо чаще. Общие экспериментальные стандарты и большой банк наборов данных, поддерживаемый группой машинного обучения в Калифорнийском университете в Ирвайне, творят чудеса и толкают науку вперед. Как мы увидим, лучшие шансы создать универсальный обучающийся алгоритм — у синтеза идей из разных парадигм.

Конечно, мало уметь выявить переобучение: прежде всего надо научить­ся его избегать. Это означает вовремя остановить даже потенциально превосходную подгонку под данные. Один из методов — применение тестов статистической значимости для проверки того, что схемы, которые мы видим, действительно существуют. Например, и правило, включающее 300 положительных примеров против 100 отрицательных, и правило, включающее три положительных примера против одного отрицательного, на обучающих данных точны в 75 процентах, однако первое правило почти наверняка лучше, чем бросок монетки, в то время как второе — нет, поскольку четыре броска «правильной» монетки легко могут дать три орла. Если в какой-то момент при составлении правила не получается найти условия, которые значительно улучшили бы его точность, нужно просто остановиться, даже если оно все еще охватывает некоторые отрицательные примеры. Точность правила на обучающей выборке окажется меньше, но, вероятно, оно будет более точным обобщением, а именно это нас на самом деле интересует.

Но и это еще не все. Если я попробую одно правило и оно окажется в 75 процентах точным на 400 примерах, я, вероятно, ему поверю. Но если я перепробую миллион правил и лучшее будет точным в 75 процентах из 400 примеров, я, вероятно, ему не поверю, потому что это вполне могло произойти случайно. Это та же проблема, с которой вы сталкиваетесь при выборе паевого фонда. Фонд «Ясновидец» десять лет подряд был лидером рынка. Ух ты! Наверное, у них гениальный управляющий! Или нет? Если у вас есть возможность выбирать из тысячи фондов, велик шанс, что десять лет лидером будет даже такой фонд, которым тайно управляют бросающие дротики мартышки. Научная литература тоже страдает от этой проблемы. Тесты статистической значимости — золотой стандарт при допуске результатов исследований к публикации, но, если эффект ищет несколько коллективов, а находит его только один, есть вероятность, что произошла ошибка, хотя по солид­ной на вид статье этого никак не определить. Одним из решений была бы публикация и положительных, и отрицательных результатов, чтобы читатель знал обо всех неудачных попытках, но такой подход не прижился. В машинном обучении можно отслеживать, сколько правил было испробовано, и соответствующим образом подбирать тесты значимости, однако тогда появляется тенденция выбрасывать много хороших правил, а не только плохих. Метод немного лучше — признать, что некоторые ложные гипотезы неизбежно прокрадутся, и держать их количество под контролем, отбрасывая гипотезы с низкой значимостью и тестируя оставленные на дальнейших данных.

Еще один популярный подход — отдавать предпочтение более простым гипотезам. Алгоритм «разделяй и властвуй» косвенно предпочитает простые правила, потому что условия перестают прибавляться к правилу, как только оно охватывает только положительные примеры, и перестает добавлять правила, как только все положительные примеры охвачены. Тем не менее для борьбы с переобучением нужно более сильное предпочтение простым правилам, которое остановит добавление условий еще до того, как будут охвачены все негативные примеры. Например, можно вычитать из точности штрафные очки, пропорциональные длине правила, и использовать это как средство оценки.

Предпочтение более простым гипотезам широко известно как бритва Оккама, однако в контексте машинного обучения этот принцип немного обманчив. «Не множить сущее без необходимости», как часто перефразируют бритву, означает только то, что нужно выбирать самую простую теорию, которая подходит к данным. Оккам, наверное, пришел бы в недоумение от мысли, что нам надо отдавать предпочтение теории, которая не идеально подходит к доказательствам, только на том основании, что она более качественно обобщает. Простые теории предпочтительнее не потому, что они обязательно точнее, а потому, что они означают меньшую когнитивную нагрузку (для нас) и меньшие вычислительные затраты (для наших алгоритмов). Более того, даже самые замысловатые модели — обычно лишь существенное упрощение реальности. Из теоремы о бесплатных обедах мы знаем, что даже в случае теорий, идеально подходящих к данным, нет гарантии, что простейшая обобщает лучше всего, а на практике одни из лучших обучающихся алго­ритмов — например, бустинг и метод опорных векторов — извлекают на первый взгляд необоснованно сложные модели. (Мы посмотрим, почему они работают, в главах 7 и 9.)

Если точность обучающегося алгоритма в тестовой выборке разо­чаровы­вает, надо диагностировать проблему: дело в слепоте или галлюцинациях? В машинном обучении для этих проблем существуют специальные термины: смещение и дисперсия. Часы, которые постоянно опаздывают на час, имеют большое смещение, но низкую дисперсию. Если часы беспорядочно идут то быстро, то медленно, но в среднем показывают правильное время, дисперсия высокая, но смещение низкое. Представьте, что вы сидите в баре с друзьями, выпиваете и играете в дартс. Вы втайне от них годами тренируетесь, добились мастерства, и все дротики попадают прямо в яблочко. У вас низкое смещение и низкая дисперсия, что показано в нижнем левом углу этой диаграммы:

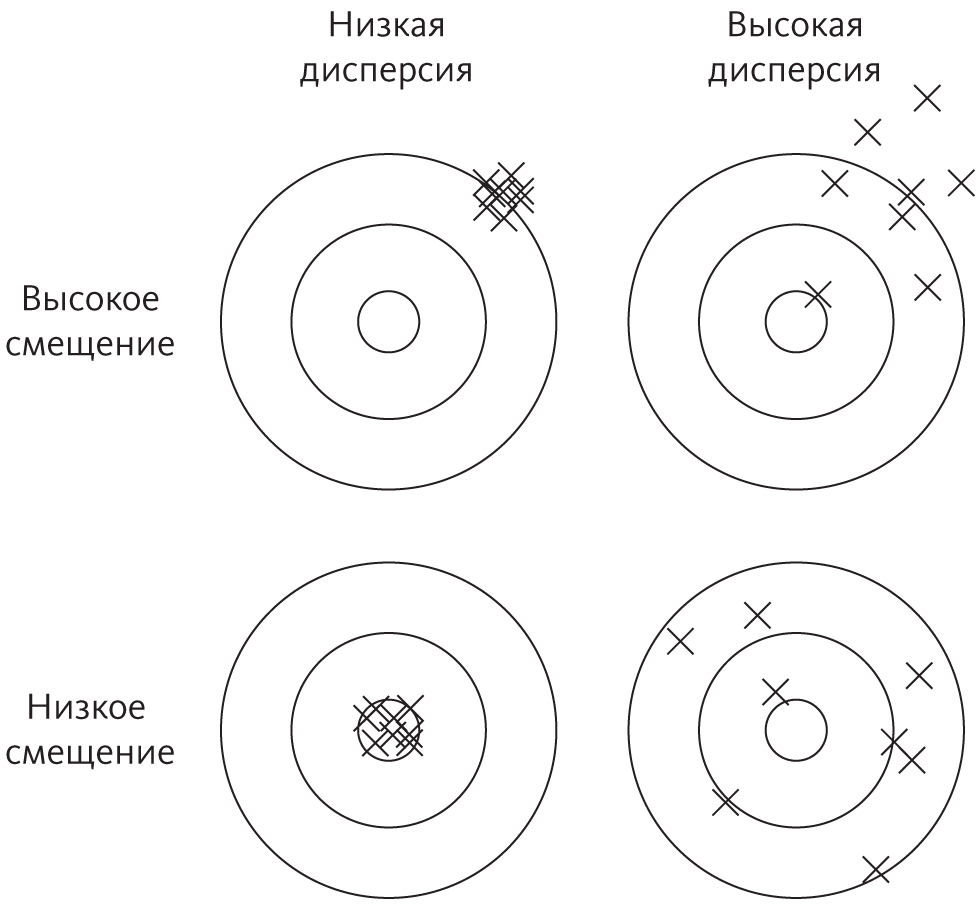
Ваш друг Бен тоже очень хорош, но сегодня вечером немного перебрал. Его дротиками утыкана вся мишень, но тем не менее он громко заявляет, что в среднем попал в десятку. (Может быть, ему надо было посвятить себя статистике.) Это случай низкого смещения и высокой дисперсии, показанный в правом нижнем углу. Подруга Бена Эшли попадает стабильно, но у нее есть склонность метить слишком высоко и вправо. Дисперсия у нее низкая, а смещение высокое (левый верхний угол). Коди никогда до этого не играл в дартс. Он попадает куда угодно, только не в центр. У него и высокое смещение, и высокая дисперсия (вверху справа).

Вы можете оценить смещение и дисперсию обучающегося алгоритма, сравнив его прогнозы после обучения на случайных вариациях обучающей выборки. Если он продолжает повторять те же самые ошибки, проблема в смещении и нужно сделать его эластичнее (или просто взять другой). Если в ошибках алгоритма нет никакой схемы, проблема в дисперсии и надо либо попробовать менее гибкий, либо получить больше данных. У большинства обучающихся алгоритмов есть «ручка», с помощью которой можно отрегулировать гибкость: это, например, порог значимости и штрафы за размер модели. Подстройка — первое, что нужно попробовать.

Индукция — противоположность дедукции

Более глубокая проблема, однако, заключается в том, что большинство обучающихся алгоритмов начинают с очень скромного объема знаний, и никакая подстройка не сможет вывести их к финишной черте. Без руко­водства знаниями, равными по объему содержимому мозга взрослого человека, они легко сбиваются с курса. Простое допущение, что вы знаете форму правды (например, что это маленький набор правил), — совсем немного, хотя из этого исходит большинство алгоритмов. Строгий эмпирик заметил бы, что это все, что закодировано в архитектуре головного мозга новорожденного. И действительно, дети подвержены переобучению чаще, чем взрослые, однако мы хотели бы учиться быстрее, чем младенцы (даже если не считать колледж, 18 лет — это все равно долго). Верховный алгоритм должен уметь начинать с большого объема знаний, заложенных людьми или выученных в предыдущие заходы, и использовать его для извлечения из данных новых обобщений. Этот подход практикуют ученые, и это далеко не «чистая доска». Индукционный алгоритм, основанный на правиле «разделяй и властвуй», на это не способен, но это может сделать другой способ формулировки правил.

Главное — понять, что индукция — просто обратный дедукции процесс, точно так же как вычитание — это противоположность деления, а интегрирование — противоположность дифференцирования. Идея была впервые предложена Уильямом Стэнли Джевонсом в конце первого десяти­летия XIX века. В 1988 году англичанин Стив Магглтон и австралиец Рэй Бантайн разработали первый практический алгоритм, основанный на этом принципе. Стратегия брать хорошо известную операцию и выводить ее противоположность имеет в математике долгую историю. Применение этого принципа к сложению привело к изобретению целых чисел, потому что без отрицательных чисел сложение не всегда имеет противоположность (3 – 4 = –1). Аналогично применение его к умножению привело к открытию рациональных чисел, а возведение в квадрат дало комплексные числа. Давайте посмотрим, можно ли применить этот принцип к дедукции. Вот классический пример дедуктивного рассуждения:

Сократ — человек.

Все люди смертны.

Следовательно…

Первое утверждение — факт о Сократе, а второе — общее правило о людях. Что из этого следует? Конечно, что Сократ смертен, если применить это правило к Сократу. При индуктивном рассуждении мы вместо этого начинаем с исходного факта следствия и ищем правило, которое позволило бы вывести второе из первого:

Сократ — человек.

………

Следовательно, Сократ смертен.

Одним из таких правил будет: если Сократ — человек, значит, он смертен. Это правило соответствует условиям задачи, но не очень полезно, потому что не специфично для Сократа. Однако теперь мы применим принцип Ньютона и обобщим правило до всех сущностей: если сущность — человек, значит, она смертна. Или, более сжато: все люди смертны. Конечно, было бы опрометчиво выводить это правило на примере одного только Сократа, однако нам известны аналогичные факты о других людях:

Платон — человек. Платон смертен.

Аристотель — человек. Аристотель смертен.

И так далее.

Для каждой пары фактов мы формулируем правило, которое позволяет нам вывести второй факт из первого и обобщить его благодаря принципу Ньютона. Если одно и то же общее правило выводится снова и снова, можно с определенной уверенностью сказать, что оно верно.

Пока что мы еще не сделали ничего такого, чего бы не умел алгоритм «разделяй и властвуй». Однако предположим, что вместо информации, что Сократ, Платон и Аристотель — люди, мы знаем только, что они философы. Мы по-прежнему хотим сделать вывод, что они смертны, и до этого сделали вывод или нам сказали, что все люди смертны. Чего не хватает теперь? Другого правила: все философы — люди. Это тоже вполне обоснованное обобщение (как минимум пока мы не решим проб­лему искусственного интеллекта и роботы не начнут философствовать), и оно заполняет пробел в наших рассуждениях:

Сократ — философ.

Все философы — люди.

Все люди смертны.

Следовательно, Сократ смертен.

Кроме того, мы можем выводить правила исключительно на основе других правил. Если мы знаем, что все философы — люди и все философы смертны, то можем индуцировать, что все люди смертны. (Мы не можем, однако, сделать вывод, что все смертные — люди, потому что нам известны другие смертные существа, например кошки и собаки. С другой стороны, ученые, люди искусства и так далее — тоже люди и тоже смертны, а это укрепляет правило.) В целом чем больше правил и фактов у нас есть изначально, тем больше возможностей индуцировать новые правила путем обратной дедукции. А чем больше правил мы индуцируем, тем больше можем индуцировать. Это положительная спираль создания знаний, которая ограничена только риском переобучения и вычислительной сложностью. Но от этих проблем исходные знания тоже помогают: если вместо одной большой дыры надо заполнить много маленьких, этапы индукции будут менее рискованными и, следовательно, менее подверженными переобучению. (Например, при том же количестве примеров выведение путем индукции правила, что все философы — люди, менее рискованно, чем вывод, что все люди смертны.)

Обратить операцию часто бывает сложно, потому у нее может быть несколько противоположностей: например, у положительного числа есть два квадратных корня — положительный и отрицательный (2² = (–2)² = 4). Самый знаменитый пример — то, что интеграл производной функции воссоздает эту функцию лишь до постоянной. Производная функции говорит нам, насколько она идет вверх и вниз в данной точке. Сложение всех этих изменений возвращает нам эту функцию, за исключением того, что мы не знаем, где она началась. Мы можем «проматывать» интеграл функции вверх или вниз без изменения производной. Чтобы упростить проблему, функцию можно «сжать», предположив, что аддитивная постоянная равна нулю. У обратной дедукции схожая проблема, и одно из ее решений — принцип Ньютона. Например, из правил «Все греческие философы — люди» и «Все греческие философы смертны» можно сделать вывод «Все люди смертны» или просто «Все греки смертны». Однако зачем довольствоваться более скромным обобщением? Вместо этого лучше предположить, что все люди смертны, пока не появится исключение. (Которое, по мнению Рэя Курцвейла, скоро появится.)

Одна из важных областей применения обратной дедукции — прогнозирование наличия у новых лекарств вредных побочных эффектов. Неудачное тестирование на животных и клинические испытания — главная причина, по которой разработка новых лекарств занимает много лет и стоит миллиарды долларов. Путем обобщения молекулярных структур известных токсичных веществ можно будет создать правила, которые быстро «прополют» предположительно многообещающие соединения и значительно увеличат шанс успешного прохождения испытаний оставшимися.

Как научиться лечить рак

В целом обратная дедукция — прекрасный путь к новым знаниям в биологии, а это первый шаг к лечению рака. Центральная догма гласит, что все, что происходит в живой клетке, в итоге контролируется генами посредством белков, синтез которых гены инициируют. В результате клетка похожа на крохотный компьютер, а ДНК — на действующую в нем программу: измените ДНК, и клетка кожи может стать нейроном, а мышиная клетка — превратиться в человеческую. В компьютерной программе все ошибки на совести программиста, но в клетке сбои происходят спонтанно, например под действием радиации или из-за ошибок при копировании: гены могут меняться, удваиваться и так далее. В большинстве случаев такие мутации приводят к тихой смерти клетки, но иногда она начинает расти, бесконтроль­но делиться, и человек заболевает раком.

Чтобы вылечить рак, нужно остановить воспроизведение больных клеток, не повредив при этом здоровые. Для этого необходимо знать, чем они отличаются и, в частности, чем отличаются их геномы, поскольку все остальное — следствие. К счастью, секвенирование генов становится рутинной и доступной процедурой, а с его помощью можно научиться предсказывать, какие лекарства будут работать против конкретных генов рака: это совсем не похоже на традиционную химиотерапию, при которой уничтожаются все клетки без разбора. Чтобы узнать, какие лекарства сработают против определенных мутаций, требуется база данных пациентов, геномов их опухолей, проверенных лекарств и исходов. Простейшие правила кодируют прямые соответствия между генами и лекарствами. Когда секвенирование геномов опухолей и сопо­ставление исходов лечения станет стандартной практикой, будет открыто много подобных правил.

Однако это только начало. Большинство видов рака представляют собой комбинацию мутаций, и лекарства для их лечения пока еще не изобретены. Поэтому следующий шаг — сформулировать правила с более сложными условиями, учитывающими геном рака, геном паци­ента, историю болезни, известные побочные эффекты препаратов и так далее. Однако важнейшая цель — составить полную модель функционирования клетки. Это позволит нам симулировать на компьютере результаты последствия мутаций у конкретного пациента, а также действие различных комбинаций лекарств, уже существу­ющих и потенциально возможных. Главные источники информации для построения таких моделей — это секвенсоры ДНК, микрочипы для анализа экспрессии генов и биологическая литература. Соединить эту информацию — очень подходящее задание для обратной дедукции.

Адам, робот-ученый, с которым мы уже знакомы, дает представление о том, как это может выглядеть. Его задача — разобраться, как работает дрожжевая клетка. Все начинается с базовых знаний о генетике и мета­болизме дрожжей и уже собранных данных об экспрессии генов в дрожжевых клетках. Затем Адам с помощью обратной дедукции выдвигает гипотезы о том, какие гены кодируют какие белки, проектирует эксперименты с ДНК-микрочипами, чтобы проверить гипотезы, затем корректирует их и переходит к следующему циклу. Будет ли происходить экспрессия данного гена, зависит от других генов и средовых факторов, и итоговую сеть взаимодействий можно представить в виде набора правил, например:

Если температура высокая, ген A активен.

Если ген A активен, а ген B — нет, происходит экспрессия гена C.

Если ген C активен, экспрессии гена D не будет.

Если бы мы знали первое и третье правила, но не знали второго и у нас были бы данные с ДНК-микрочипа, где при высокой температуре экспрессии B и D не наблюдается, то могли бы вывести второе правило путем обратной дедукции. Когда у нас будет это правило и, возможно, мы подтвердим его путем эксперимента с микрочипом, его можно будет использовать как основу для дальнейших выводов путем индукции. Аналогичным путем можно собрать воедино цепочки химических реакций, благодаря которым белки выполняют свою функцию.

Однако недостаточно просто знать, как происходит взаиморегуляция генов и как организована сеть белковых реакций в клетке. Нужна информация, сколько именно вырабатывается молекул каждого вещества. Микрочипы ДНК и другие эксперименты могут предоставить такую количественную информацию, но обратная дедукция с ее логическим характером «все или ничего» не очень хорошо подходит для подобных задач. Для этого нам понадобятся коннекционистские методы, с которыми мы познакомимся в следующей главе.

Игра в двадцать вопросов

Другое ограничение обратной дедукции заключается в том, что оно требует большого объема вычислений и из-за этого его трудно применять к масштабным наборам данных. Для решения этой проблемы символисты прибегают к индукции с помощью дерева решений. Деревья решений можно считать ответом на вопрос, что делать, если к какому-то частному случаю применимы правила не одного, а целого ряда понятий. Как в таком случае решить, к какому понятию принадлежит этот случай? Если перед нами частично скрытый предмет с плоской поверхностью и четырьмя ножками, как понять, стол это или стул? Один из вариантов — упорядочить правила, например, в порядке уменьшения точности и выбрать первое подходящее. Другой — дать правилам проголосовать. Деревья решений же априори гарантируют, что к каждому случаю будет подобрано ровно одно правило. Это будет так, если каждая пара правил отличается как минимум в одном тестировании атрибутов и такой набор правил можно выстроить в виде дерева решений. Например, посмотрите на следующий набор:

Если вы за уменьшение налогов и против абортов, вы республиканец.

Если вы против уменьшения налогов, вы демократ.

Если вы за уменьшение налогов, за право на аборт и за свободный оборот оружия, вы независимый кандидат.

Если вы за уменьшение налогов, за право на аборт и против свободного оборота оружия, вы демократ.

Все это можно организовать в виде следующего дерева решений:

Дерево решений — как игра в «20 вопросов» с каждым случаем. Начиная с корня каждый узел спрашивает про значение одного атрибута, и, в зависимости от ответа, мы следуем по той или иной ветви. Когда мы достигаем «листа» дерева, на нем нас ждет предсказанное понятие. Каждый путь от корня до листа соответствует правилу. Если принцип напоминает вам о длинной серии вопросов, через которые приходится проходить, чтобы дозвониться в клиентскую службу, это не случайно: раздражающие голосовые меню тоже деревья решений. Компьютер на другом конце провода играет с вами в ту же самую игру, чтобы понять, чего вы хотите. Каждый пункт меню — это вопрос.

Согласно дереву решений выше, вы либо республиканец, либо демократ, либо независимый кандидат. Невозможна ситуация, когда этих вариантов больше чем один или ни одного. Наборы понятий, обладающие этим свойством, называют наборами классов, а алгоритмы, которые их определяют, — классификаторами. Каждое понятие косвенно определяет два класса: оно само и его отрицание (например, спам и не-спам). Классификаторы — самая широко распространенная форма машинного обучения.

Обучать деревья решений можно с помощью одного из вариантов алго­ритма «разделяй и властвуй». Сначала надо выбрать атрибут, который будет протестирован у корня. Затем мы сосредоточимся на примерах с нисходящих ветвей и выберем для них следующие тесты (например, проверим, за или против абортов сторонники уменьшения налогов). Процесс будет повторяться для каждого нового узла, который мы получим путем индукции, пока все примеры в ветви не будут принадлежать к одному классу. В этот момент мы присвоим этой ветви данный класс.

Напрашивается вопрос: как выбрать лучший атрибут для тестирования в узле? Точность — количество правильно предсказанных примеров — работает не очень хорошо, потому что мы не пытаемся предсказать конкретный класс, а, скорее, стремимся постепенно разделять классы, пока не «очистим» все ветви. Это заставляет вспомнить понятие энтропии из тео­рии информации. Энтропия набора предметов — мера его неупорядоченности. Если в группе из 150 человек будет 50 республиканцев, 50 демократов и 50 независимых кандидатов, ее политическая энтропия максимальна. С другой стороны, если в группе одни республиканцы, энтропия будет равна нулю, во всяком случае, в отношении партийной принадлежности. Поэтому, чтобы получить хорошее дерево решений, мы выберем в каждом узле атрибут, который в среднем даст самую низкую энтропию классов по всем ее ветвям, с учетом количества примеров в каждой из ветвей.

Как и в случае обучения правилам, мы не хотим получить дерево, которое будет идеально предсказывать классы всех примеров в обучающей выборке, потому что это будет, вероятно, переобучением. Для его предотвращения мы, опять же, можем использовать тесты значимости или штрафные очки для больших размеров дерева.

Иметь отдельную ветвь для каждого значения атрибута неплохо, если они дискретные. А как насчет числовых атрибутов? Если выделять ветвь для каждого значения непрерывной переменной, дерево окажется бесконечно широким. Простое решение — выбрать ряд ключевых порогов на основе энтропии и использовать их. Например, «температура пациента выше или ниже 37,7 °C?». Для выявления у человека инфекции этой информации в сочетании с другими симптомами может быть достаточно.

Деревья решений находят применение во многих областях. Так, они делают важную работу в психологии. Эрл Хант и его коллеги пользовались деревьями решений в 1960 году для моделирования усвоения человеком новых концепций, а один из магистрантов Ханта, Джон Росс Куинлан, попробовал использовать их в шахматах. Его первоначальная цель была скромной: предсказать результаты эндшпилей «король и ладья против короля и ферзя» на основе ситуации на доске. Теперь же дерево решений, согласно опросам, стало самым широко используемым алгоритмом машинного обучения, что неудивительно: эту методику легко понять и освоить, и обычно она дает довольно точный результат без лишних настроек. Куинлан — самый выдающийся исследователь в школе символистов. Этот невозмутимый прагматичный австралиец год за годом неустанно улучшал деревья решений, сделал их золотым стандартом в области классификации и пишет о них удивительно ясные статьи.

Что бы вы ни хотели предсказать, очень вероятно, что кто-то уже использовал для этого деревья решений. С их помощью разработанный Microsoft игровой контроллер Kinect определяет положение частей тела, получая сигналы от сенсоров глубины, и передает информацию в приставку Xbox. В 2002 году деревья решений обошли группу экспертов, правильно предсказав три из каждых четырех постановлений Верховного суда, в то время как люди дали менее 60 процентов правильных ответов. «Тысячи поклонников деревьев решений не могут ошибаться!» — думаете вы и набрасываете свое дерево, чтобы угадать ответ девушки на ваше приглашение:

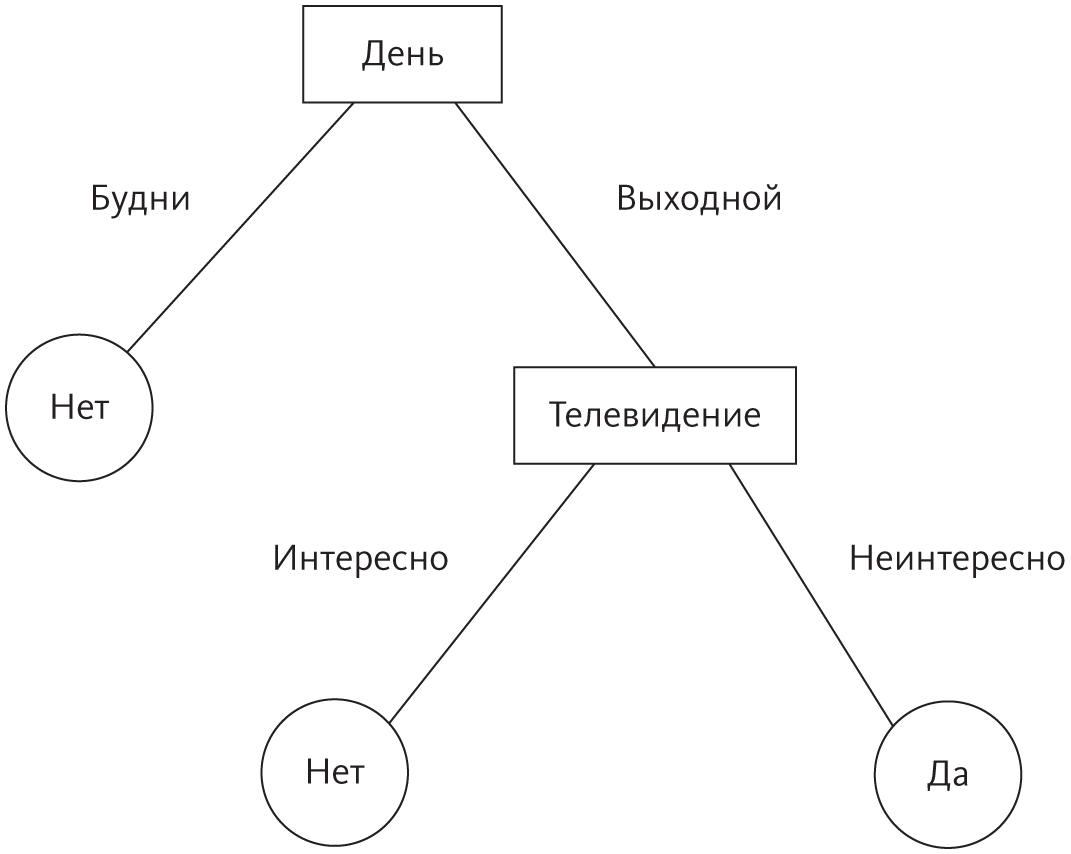
Получается, что сегодня вечером она скажет «да». Вы делаете глубокий вдох, достаете телефон и набираете ее номер.

Символисты

Важнейшее убеждение символистов заключается в том, что интеллект можно свести к манипулированию символами. Математик решает уравнения, переставляя символы и заменяя одни другими согласно заранее определенным правилам. Так же поступает логик, когда делает выводы путем дедукции. Согласно этой гипотезе, интеллект не зависит от носи­теля: можно писать символы мелом на доске, включать и выключать транзисторы, выражать их импульсами между нейронами или с помощью конструктора Tinkertoys. Если у вас есть структура, обладающая мощью универсальной машины Тьюринга, вы сможете сделать все что угодно. Программное обеспечение можно вообще отделить от «железа», и, если вы хотите просто разобраться, как могут учиться машины, вам (к счастью) не надо волноваться о машинах как таковых, за исключением приобретения ПК или циклов на облаке Amazon.

Веру символистов в мощь манипуляций символами разделяют многие другие информатики, психологи и философы. Психолог Дэвид Марр утверждает, что любую систему обработки информации нужно рассмат­ривать на трех уровнях: фундаментальные свойства проблемы, которую она решает, алгоритмы и представления, которые используются для ее решения, и их физическое воплощение. Например, сложение можно определить набором аксиом, не зависящих от того, как оно выполняется. Числа можно выразить по-разному (например, римскими и арабскими цифрами) и складывать с использованием разных алгоритмов, а алго­ритмы могут выполняться на абаке, карманном калькуляторе или даже — что очень неэффективно — в уме. Обучение — яркий пример когнитивной способности, которую мы можем плодотворно изучать с точки зрения уровней Марра.

Символистское машинное обучение — ответвление инженерии знаний, одной из школ искусственного интеллекта. В 1970-х у так называемых систем на основе знаний были очень впечатляющие успехи, в 1980-х они быстро распространились, но потом вымерли. Главная причина — печально известное «узкое горло» приобретения знаний: получать информацию от экспертов и кодировать в виде правил слишком сложное, трудоемкое и подверженное ошибкам занятие, поэтому для большинства проблем такой подход нецеле­сообразен. Оказалось, что намного легче позволить компьютеру автоматически учиться, скажем, диагностировать заболевания путем просмотра в базах данных симпто­мов и исходов, чем без конца опрашивать врачей. Внезапно работы таких первопроходцев, как Рышард Михальский, Том Митчелл и Росс Куинлан, приобрели новую значимость, и с тех пор дисциплина непрерывно развивается. (Еще одной важной проблемой систем, основанных на знаниях, было то, что им сложно работать с неопределенностью. Подробнее мы поговорим об этом в главе 6.)

Благодаря своему происхождению и основополагающим принципам символистское машинное обучение ближе к другим областям науки об искусственном интеллекте, чем другие школы машинного обучения. Если информатику представить в виде континента, у символизма будет длинная граница с инженерией знаний. Обмен информацией происходит в обоих направлениях: обучающиеся алгоритмы используют введенное вручную знание, а знание, полученное путем индукции, пополняет базы знаний. Тем не менее вдоль этой границы проходит разлом между рационалистами и эмпириками, и пересечь ее непросто.

Символизм — кратчайший путь к Верховному алгоритму. Он не требует разбираться, как работает эволюция или головной мозг, и позволяет обойтись без сложной математики байесианства. Наборы правил и деревья решений просты для понимания, и поэтому пользователь представляет себе, что замышляет обучающийся алгоритм, ему легче отличить правильные действия от неправильных, при необходимости внести поправки и быть уверенным в результатах.

Но несмотря на популярность деревьев решений, более удобный исходный пункт для поисков Верховного алгоритма — обратная дедукция. У нее есть критически важное качество: в нее легко встраивать знания, а, как нам уже известно, из-за проблемы Юма это существенное преимущество. Кроме того, наборы правил — экспоненциально более компактный способ представления большинства понятий, чем деревья решений. Превратить дерево решений в набор правил несложно: каждый путь от корня к листу становится правилом, и нет никаких подводных камней. С другой стороны, если нужно превратить в дерево решений набор правил, в худшем случае придется разворачивать каждое из них в мини-дерево решений, а затем заменять каждый листок дерева, полученного из правила один, копией дерева для правила два, каждый листок каждой копии правила два копией правила три и так далее, что порождает серьезные проблемы.

Обратная дедукция как сверхученый. Он будет систематически рассматривать доказательства, взвешивать возможные выводы, сопоставлять лучшие и использовать их вместе с другими доказательствами для формулировки дальнейших гипотез, и все это с компьютерной скоростью. Это чисто и изящно, по крайней мере на вкус символиста. С другой стороны, у метода есть ряд серьезных недостатков. Количество возможных выводов очень велико, и, чтобы не заблудиться, приходится не держаться близко к исходному знанию. Обратную дедукцию легко запутать шумом: как разобраться, каких шагов в дедукции не хватает, если предположения или заключения ложны? Еще более серьезно то, что реальные понятия очень часто не определяются сжатым набором правил. Они не черно-белые, а находятся в большой серой зоне между, скажем, спамом и не-спамом, поэтому приходится взвешивать и накапливать слабые доказательства, пока картина не прояснится. В частности, при диагностике заболеваний одним симптомам придается большее значение, чем другим, и неполные доказательства — это нормально. Никто еще не преуспел в обучении набору правил, которое будет определять кошку, глядя на пиксели на картинке, и, наверное, это просто невозможно.

Очень критично по отношению к символистскому обучению настроены коннекционисты. Они считают, что понятия, которые можно определить с помощью логических правил, лишь вершина айсберга, а в глубине есть много такого, что формальные рассуждения просто неспособны увидеть, точно так же как значительная часть работы мозга скрыта в подсознании. Нельзя построить бесплотного автоматического ученого и надеяться, что он сделает что-то полезное: сначала надо одарить его чем-то вроде настоящего мозга, соединенного с насто­ящими органами чувств, вырастить в реальном мире, возможно, даже ставить ему время от времени подножки. Как же построить такой мозг? Путем обратной инженерии. Если вы решили построить путем обратной инженерии автомобиль, придется заглянуть под капот. Если вы хотите таким же образом создать мозг, надо заглянуть в черепную коробку.

Отправить