Назад: Chapter 6 - The Best Xbox Game: Security Hacking

Дальше: Chapter 8 - Reverse Engineering Xbox Security

Chapter 7 -
A Brief Primer on Security

Hacking the Xbox requires security hacking in addition to hardware and firmware hacking, as you discovered in the last chapter. We will go over some of the possible motivations behind adding sophisticated security to something as mundane as a gaming machine, and then we will dive into the basic principals and algorithms necessary to understand and appreciate the Xbox’s security mechanisms.

Who Needs Security, Anyways?

The video game console is a toy for most people: it’s low cost, consumer electronics. Why did Microsoft go through such pains to secure their system? In the game of security hacking, quite frequently understanding the motive of the securer is helpful in finding weaknesses that you can exploit.

Cryptography is not security. Cryptography is a means to an end for security, but real security involves the entire system architecture, including the end users. As Kevin Mitnick said in a recent Slashdot interview, “. . . security is not a product that can be purchased off the shelf, but consists of policies, people, processes, and technology.”¹ I believe that security is fundamentally a social concept. In practice, you can open your windows and leave the front door locked and people won’t just walk in through your window or pick your doorlock, even though both are relatively easy tasks. Locked doors and open windows work because a locked door is mostly a symbolic measure; it forces an intruder to make a conscious act of violation in order to enter a house, and that alone is enough to separate criminals from well-doers. Sony’s Playstation console has a good example of front-door lock security. The mechanism used to copy-protect their games is simple, involves no cryptography, and is easily overridden with easily installed, inexpensive hardware modifications. Despite this, sales numbers indicate that purchasing Playstation games has not gone out of style; the front-door lock is working.

Microsoft employs a variation of front-door lock style security. Video games for the Xbox are distributed using the (so far) uncopyable DVD-9 format, a single-sided, dual layer media format. User-writeable DVDs, on the other hand, are always in DVD-5 format, a single-sided, single layer media format. DVD-9 capable burners are not likely to be available soon due to the difficulty in making a writing system capable of burning one layer without affecting the integrity of the other layer. Thus, by distributing security data between the two layers of a DVD-9 disk and requiring a game executable to come from DVD-9 media, Microsoft has a fairly effective front-door lock on its video games. By judiciously requiring the DVD-9 format, Microsoft has pretty much forced any potential game copier into a realm where some kind of hardware modification is necessary.

Why then would Microsoft risk investing in such a complex security scheme on the Xbox? Is Microsoft’s main motivation really to quell piracy? It is quite possible that in fact the primary reason for the rest of the Xbox security system—the secure boot sectors, signed executables, trust relationships and encrypted/authenticated network protocols — lies not in antipiracy measures.

One possible motivation for all the security is to prevent the use of the Xbox console for any purpose other than gaming. The Xbox console is in the unique position of being an almost 100 percent stock PC. Unlike the Gamecube and the Playstation2, there is an enormous body of software that seems like it should just run on the Xbox, given the right BIOS programming. To make matters worse, Microsoft loses much more money on its console hardware than its competitors. Some estimate that its losses may be as high as $200 per console, assuming the most recent retail price of $199. Hence, it is in Microsoft’s interest to try and ensure that it is not selling subsidized GNU/Linux boxes. However, even this is probably not Microsoft’s main goal. The Xbox’s 64 MB of main memory, lack of a keyboard or mouse out of the box, and a fairly slow processor by today’s standards makes it less appealing than, for example, the $200 Microtel PC available at Walmart as of late 2002. In addition, Microsoft has deep pockets; if the Xbox gained market traction and outsold Sony’s Playstation2, Microsoft would only have to stomach a few billion dollars of upfront loss — relatively small in comparison to the roughly $40 billion cash-pile on which it sits. Thus, it is quite possible that the critical mission of Xbox security is not to prevent alternative console uses or to deter piracy.

Perhaps the real reason for the complex security of the Xbox is to ensure the success of Xbox Live, Microsoft’s on-line gaming service. Microsoft’s marketing hype and PR statements indicate that it is betting on the success of Xbox Live to drive hardware sales. Furthermore, Xbox Live is a subscription service, and one year from its launch users will have to pay a monthly fee. If Microsoft can get its subscribers hooked on Xbox Live, then all of a sudden the Xbox business looks quite profitable, even if a substantial amount of money is lost up-front on the hardware. The trick is, of course, hook Xbox users on Xbox Live. Billed as the “Disneyland of on-line gaming,” the goal of Xbox Live is to provide a well-executed and fair gaming experience. Central to the value proposition of Xbox Live that there are no cheaters. In order to ensure that nobody is cheating, users must be forced to authenticate themselves against a registry maintained by Xbox Live, and their game state must be kept secure and unmodifiable. In addition, game software must be unpatched. Even more crucial is the fact that you only need a few cheaters to ruin the gaming experience of an entire user base. All of a sudden, the front-door security protections offered by the DVD-9 format seem inadequate. The odds are against you if you betting the success of a business on the morality and honor of a user base of millions of twenty-something hardcore male gamers with a reasonable amount of computer savvy distributed throughout. The hardware must be trustable, network connections secure, and executables signed and sealed.

The statement that the hardware must be trustable bears repeating. Given an untrustable user base, the only way to establish a trust relationship with clients is if a seed of trust exists in every piece of hardware. Hence, Microsoft must include in every client a piece of tamper-proof hardware that enables some kind of attestation. Attestation is the ability to prove that some piece of data, such as a player’s identity or game state, is in fact generated by untainted software and hardware. The tamper-proof hardware does not have to implement the attestation function directly, but it must at least ensure that the system is in a trustable state before attestation.

There are many ways to ensure that hardware is trustable. The brute-force method is to make the entire piece of hardware physically secure. Automated Teller Machines are prime examples of hardware that is physically secure. Sealed in thick sheet metal and covered with intrusion sensors, it is difficult to physically penetrate and modify the hardware of an ATM. Stil , hile effective, this is an impractical and expensive solution for a video game console. A more economical solution is to use a small piece of trusted tamper-proof hardware that can make “measurements” on the rest of the system. These sorts of measurements are typically accomplished through the use of a cryptographic hash function. If all of these trust measurements conform with the expected values, then one might be able to conclude that the entire system is trustable.

I say might because this scheme is still vulnerable to man-in-the-middle attacks where a hacker sends spoofed valid data in response to a measurement query. Man-in-the-middle attacks refer to a general class of attacks where an adversary can freely modify and control the information being passed between two parties. Because of the man-in-the-middle weakness, it does not make sense to use an extremely sophisticated tamperproof module to make the system measurements. A single packaged silicon chip is probably good enough, as it is typically easier to intercept and spoof the measurement data going past on a printed circuit board than it is to penetrate the epoxy package of a chip and modify the chip’s circuitry.

The trust measurement system can be implemented using a measure-once approach. Starting with the processor cold-boot sequence, every piece of code is measured for trust before execution. If the processor never executes untrusted code, then what is there not to trust? This scheme requires a very simple tamper-proof hardware module — a tamper-proof ROM that stores the cold-boot code, a “seed” of trust. The type of cryptography used for the measurement and verification process is typically a combination of hashes and public-key cryptography. Public-key cryptography is preferred for this application because the private key required to generate a valid code segment is a secret kept by only the hardware vendor. Again, this scheme is vulnerable to many kinds of man-in-the-middle attacks, as well as pure cryptographic attacks and attacks on the implementation of the system.

A Brief Primer on Cryptography

ci·pher ( n): 1 a: ZERO b: one that has no weight, worth, or influence : NONENTITY. 2 a: a method of transforming text in order to conceal its meaning — compare to CODE ²

Ciphers provide no security on their own. More specifically, ciphers only provide security if the key is secure, if the algorithm is strong, and if there are no back doors into the system. If someone hands you a CD-ROM encrypted with a strong cipher and locks you in a padded room with a supercomputer, the sun will probably go supernova before you can decrypt the CD-ROM. On the other hand, if you could observe and probe the machine as it was working to encrypt the CD-ROM, the encryption is moot. You could get the enciphering key by eavesdropping the keyboard. Or, you could dump the contents of the computer’s memory and obtain the plaintext without knowing the key.

The situation with the Xbox is similar to the latter. Ultimately, the Xbox must access and run the programs presented to it on valid disks. Furthermore, the Pentium CPU used in the Xbox cannot tell the difference between an authorized instruction and an unauthorized instruction. Finally, the user has full access to probe and modify the Xbox hardware. Thus, even if the Xbox uses strong ciphers, the security of keys is questionable, and there may be back doors into the system.

This section will briefly describe the kinds of cryptographic algorithms used in the Xbox. We will focus on the practical implications and implementation issues of these algorithms. You will need to understand these algorithms in order to appreciate the available attacks on the Xbox security system.

Note

I make no pretense of addressing the theoretical aspects of cryptography; those are beyond me and beyond the scope of the book. Instead, I refer interested readers to Bruce Schneier’s excellent book, Applied Cryptography (John Wiley & Sons); most of my knowledge in cryptography comes from that book. Readers who are already familiar with cryptography should be able to skim or skip the remainder of this chapter.

Classes of Cryptographic Algorithms

There are a few important classes of cryptographic algorithms used in the Xbox. These are:

• Hashes

• Symmetric ciphers

• Public key ciphers

Hashes come in several varieties. Hashes of the cryptographic variety are used to summarize or “digest” a large amount of data. The summary is a number of fixed length, typically around 100 to 200 bits long, while the source data can be of almost any size. The most important property of a hash is that it is a one-way computation. In other words, it is easy to compute the hash, but it is very difficult (see the sidebar “Very Difficult Problems” to understand exactly what this means) to derive sequences of data whose hash digest are identical or to determine anything about the original data from the hash.

The strength of a hash against finding two sequences of data that hash to the same value is referred to as its collision resistance, and in general, a good n-bit hash requires about 2n/2 random data sequences to be hashed and compared in order to cause a collision. Since hashes are designed to be very easy to compute and very collision-resistant, they are often used to detect whether a bit has been changed in large regions of secure data. For many applications, it is sufficient to include just an encrypted hash of a message in lieu of expending the computational effort to encrypt the whole message.

Symmetric ciphers are algorithms that have encryption and decryption keys that can be easily derived from one another. Most of the time, the encryption and decryption keys are the same. Symmetric ciphers use a mixing function to combine a key schedule with data that has been processed by somecryptographic function. This mixing may be repeated several times over a single block of data as in a block cipher, or it may occur once as in a stream cipher. All of the basic functions in a symmetric cipher are computationally simple, so symmetric ciphers are the preferred method for encrypting bulk data.

Typical examples of mixing functions are XORs, modular additions and modular multiplications. The simplest function, XOR, has the property that any number XOR itself is zero. The XOR operation is often denoted with a ⊕ symbol. The XOR operation also has all the usual properties of arithmetic (commutative, associative, distributive, etc.), so

(A ⊕ B) ⊕ B = A ⊕ (B ⊕ B) = A ⊕ 0 = A

Thus, if A were a message and B were a key, (A ⊕ B) would be the ciphertext, and the plaintext can be recovered by simply performing an XOR with B again.

A key schedule is an algorithm that takes a relatively short key and expands its information over a long series of bits. Key schedules are used to help diffuse the key data over a larger block of data so the relationship between the ciphertext and the key is obscured.

Very Difficult Problems

Cryptographic functions are all based on mathematical algorithms whose results are easy to compute given all the operands, but whose operands are very difficult to compute given just the result. The security of a cryptographic function is precisely the difficulty of computing these operands given just the results. Let us take a moment and explore what it means to be very difficult.

Consider the symmetric cipher AES. It uses a 128-bit key, and so far, it is strong against all known analytical cryptographic attacks, such as differential and linear cryptanalysis. When I say it is strong against analysis X, I mean that it will require at least as many operations to recover the key or plaintext using a brute-force search as it would using analysis X. A brute-force search is when I take a very fast computer and try every one of the 2¹²⁸ possible keys in order to recover the original data. Most cryptographic algorithms in common use today are strong against all known cryptanalysis techniques, so the important number to understand is the strength of a brute-force attack.

As it turns out, older algorithms such as DES, a 56-bit cipher is not a very difficult problem. It is fairly easy to build a machine using FPGAs (Field Programmable Gate Arrays) that can crack keys at an economy of about 2²² keys/second/dollar (2²² is about four million). Note that this number increases with time at a rate equivalent to Moore’s Law. Today, if you are willing to wait about a week for each key, you can recover them for about the price of a nice car. Let’s hope that banks do not use DES to encrypt their account data!

The successor to DES, AES, is a cipher that can use 128, 192, or 56-bit keys. These keys are large enough to be considered impervious to brute-force attacks (i.e., a very difficult problem). According to the AES Q&A published by NIST (http://csrc.nist.gov/encryption/aes/aesfact.html), a machine powerful enough to recover one DES key per second through brute force (trying on average 255 keys per second) would still require 149 trillion years to recover a 128-bit AES key. My favorite analysis of the strength of 256-bit keys against brute force attacks comes from Bruce Schneier’s Applied Cryptography. In his book, he uses an argument based on the amount of energy required to crack a 256-bit key. It turns out that even with a thermodynamically ideal computer, it would require over 32 times the annual energy output of our sun to just count to 2¹⁹², much less do anything useful with that count. (I must stress that all of this assumes that the most efficient attack is brute force. Who knows, maybe someone will discover a weakness in the algorithm that can be used to mount a much more efficient attack. New analysis techniques are constantly being invented that slowly chips away at the strength of a cipher.)

Public key ciphers, on the other hand, are based on a wide variety of difficult to reverse mathematical operations, such as prime number multiplication and modular exponentiation. As a result, the key space for many public key ciphers is sparse, so more key bits are required for equivalent symmetric cipher security. As an example, key lengths in the RSA public-key cipher are typically several thousands of bits long.

The exact correlation between the security of RSA public key lengths and symmetric cipher key lengths is unknown. The security of RSA is thought to be the difficulty of factoring the products of large prime numbers; however, there may be other attacks yet to be discovered on the algorithm. Even so, the effective difficulty of factoring the product of large primes is reduced not only by advances in computing technology (Moore’s Law), but also by advances in number theory, such as the invention and refinement of the Quadratic Sieve and the General Number Field Sieve. In August 1999, a group of researches used the Number Field Sieve to factor a 512-bit prime number in 7.4 calendar months, including the time required to set up the factorizing run¹. In addition, new technologies such as quantum computing promise to enable the factorization of prime numbers in polynomial time. I wouldn’t hold your breath, however; there is still debate as to whether it is possible to build a quantum computer large enough to factor an interesting prime. As of today, RSA Security, Inc. recommends key lengths of 1024 bits for most corporate uses, and 2048 bits for “extremely valuable keys”². Bruce Schneier estimates in the second edition of Applied Cryptography that a 2304 bit public key length gives the equivalent security of a 128 bit symmetric key, and that a 1792 bit public key length corresponds to about a 112 bit symmetric key.

As you read about the Xbox security scheme, keep in mind these basic guidelines about how difficult it can be to crack these security schemes using brute-force methods. Time after time, messages are posted on hacking forums and bulletin boards asking, “why don’t we start a distributed key search effort for these keys?” Now you know the answer.

¹ http://www.rsasecurity.com/rsalabs/challenges/factoring/rsa155.html

² http://www.rsasecurity.com/rsalabs/faq/3-1-5.html

A typical cryptographic function as used in a symmetric block cipher consists of a set of carefully designed substitutions, permutations, compressions and expansions. These functions serve to confuse and diffuse the plaintext. Subtle changes in any piece of a cryptographic function typically have a profound effect on the security of a cipher.

The fact that the encryption and decryption keys are closely related in a symmetric cipher makes them difficult to use in certain security applications. For example, if I wish to distribute an encrypted document to a mailing list, everyone on the mailing list must also effectively know my encryption key if they can read the document. In addition, initiating contact with a remote party is difficult, because at some point I have to transmit a key to them. Someone observing the transmission medium could steal the key and read, forge, and modify all subsequent messages.

Public key ciphers are algorithms that use a different key for encryption and decryption. They are also referred to as asymmetric ciphers for this reason. The big advantage of public key ciphers is that one of the keys can be kept a secret. This allows data exchange with untrusted users without giving the untrusted user the ability to forge or read other protected content. The down side of public key algorithms is that they typically require more complex computations and are thus slower than symmetric ciphers. Public key ciphers also tend to require longer keys for equivalent security. As a result, if a large amount of data is to be exchanged, public key ciphers are often used to encrypt a key for a symmetric cipher that is used to encrypt the bulk of the data. This symmetric cipher key can be unique to each transaction and hence it is often referred to as a “session key.”

SHA-1 Hash

SHA-1 is the Secure Hash Algorithm recommended by the Federal government in FIPS publication 180-1 (http://www.itl.nist.gov/fipspubs/fip180-1.htm). Devised by the NSA and based on Ronald L. Rivest’s MD4 message digest algorithm, SHA-1 works on messages of any length less than 264 bits in length, and it produces a 160 bit output. The SHA-1 hash algorithm starts with a deterministic 160-bit seed state; this state is blended with a block of 512 bits of message data over four rounds. Each round consists of a series of non-linear functions, rotations, shifts and XORs. The result of a round is used to seed the next round’s computation. In general, 280 random messages need to be generated, hashed and “simultaneously” compared in order to find two messages that have the same hash value (i.e., a hash collision). Finding two random messages that have the same hash is known as the “birthday attack,” named after the probabilistic phenomenon called the “birthday paradox”: the probability that two people share the same birthday in a room of 23 people is better than 50%. On the other hand, 2160 random messages need to be generated, hashed and compared in order to find a message that hashes to the same value as a specific message. Thus, the strength of a hash function depends heavily upon the manner in which it is used.

  void encipher(unsigned long *const v,unsigned long *const w,                const unsigned long *const k) {   register unsigned long            y=v[0], z=v[1], sum=0, delta=0x9E3779B9,            a=k[0], b=k[1], c=k[2], d=k[3], n=32;    while(n—>0) {      sum += delta;      y += (z << 4)+a ^ z+sum ^ (z >> 5)+b;      z += (y << 4)+c ^ y+sum ^ (y >> 5)+d;   }     w[0]=y; w[1]=z; }

Listing 7-1: TEA Algorithm in ANSI C³

TEA

TEA, or tiny encryption algorithm, was developed by David Wheeler and Roger Needham at the Computer Laboratory of Cambridge University. (The developers have a web page for TEA at http://vader.brad.ac.uk/tea/tea.shtml; much of the material presented here is gleaned from that page.)

As its name implies, TEA is a compact, fast encryption algorithm suitable for encrypting real-time data streams and embedded applications where processor performance and storage space is tight. TEA has a 128-bit key and it operates on 64-bits of data at a time, and each of its 32 rounds uses only shifts, XORs and additions. (The algorithm, given in Listing 7-1 and Figure 7-2, is optimized for implementation on 32-bit general-purpose processors.)

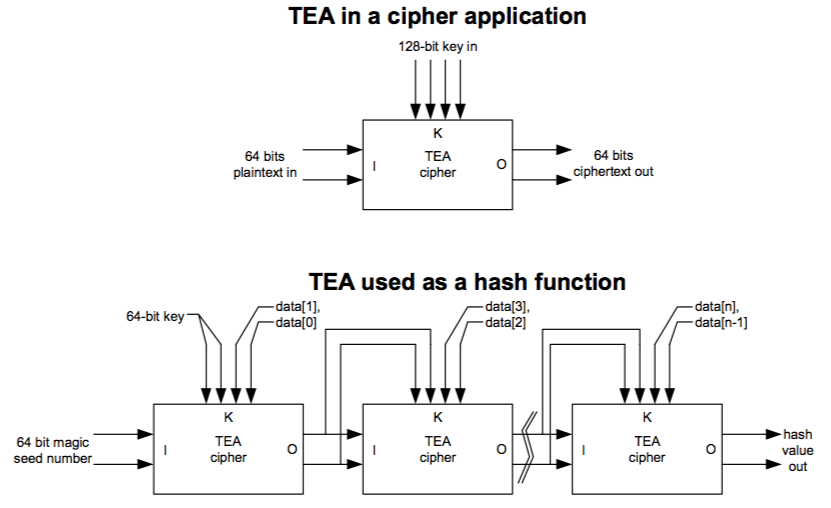
figure_7-1

Figure 7-1: Tea cipher usage scenarios.

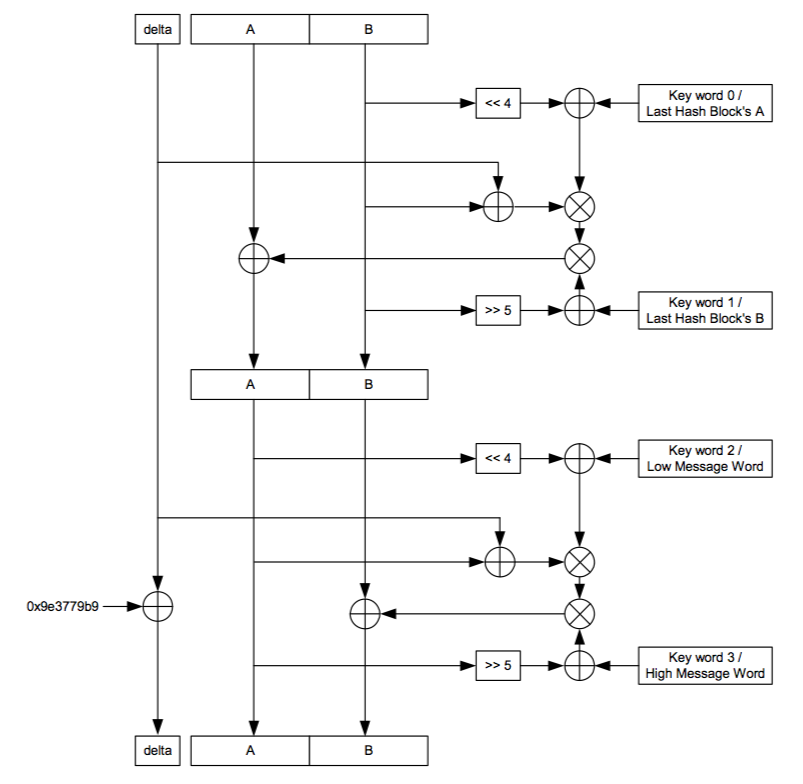
figure_7-2

Figure 7-2: Inner structure of TEA. This diagram depicts a single round of TEA, which is repeated 32 times for the full cipher. The key schedule is described in the boxes on the right for use as both a cipher and as a hashing function.

The bantam TEA algorithm is believed to be quite secure when used to encrypt and decrypt data. However, TEA is not used for encryption in the Xbox; it is actually used as a hash function by operating the cipher in a modified Davies-Meyer mode. The region to be hashed is divided into 64-bit blocks. These source data blocks are used as half of the key input to TEA. The other half of the key input comes from the result of the previous TEA operation, and the first TEA operation uses a magic number as its input.

The result is a 64-bit hash function, as depicted in Figure 7-1. This hash is weak against birthday attacks, especially given the computational efficiency of TEA, as only 2³² message pairs need to be tested on average to find a collision. Even though a birthday attack does not apply in the Xbox’s usage scenario, the Xbox runs the hash twice, each time with a different magic number seed, and concatenates the results to generate a single 128-bit hash value — probably in an attempt to foil brute-force attacks.

Unfortunately, TEA has a weakness in its key schedule: every TEA key has four related keys. In other words, for every key, you can generate three other keys that produce the same ciphertext result with the same input data. Related-key generation is as simple as complementing pairs of key bits (bits 31 and 63 is one pair, bits 95 and 127 are the other pair). This makes TEA unsuitable for use as a hash function, and this weakness is well documented in the paper “Key-schedule cryptanalysis of IDEA, G-DES, GOST, SAFER, and triple-DES,” by John Kelsey, Bruce Schneier, and David Wagner, presented many years ago at CRYPTO 1996. This weakness was later leveraged by a team headed by Andy Green to break the second version of the Xbox security scheme.

RC-4

RC-4 (Ron’s Code or Rivest Cipher 4) is a variable key-length stream cipher by Ron Rivest. The heart of RC-4 is the keystream generator. It can be thought of as a cryptographic pseudo-random number generator (CPRNG). The output of the CPRNG is XOR’d one byte at a time with a plaintext stream to generate the ciphertext. Decryption is accomplished in a similar fashion. Loosely speaking, the generator is “seeded” with a value (the key) of up to 256 bytes (2048 bits) long. If the key is shorter than 256 bytes, it is repeated to fill out the 256 bytes before use as a seed; this enables variable-length keys. In the Xbox, the key is 16 bytes (128 bits) in length, and thus the cipher is dubbed RC-4/128.

 typedef struct rc4_key {   unsigned char state[256];   unsigned char x;   unsigned char y; } rc4_key;  void prepare_key(unsigned char *key_data_ptr, int key_data_len,                 rc4_key *key) {   unsigned char swapByte, index1, index2;   unsigned char* state;   short counter;      state = &key->state[0];   for(counter = 0; counter &lt; 256; counter++)     state[counter] = counter;     key->x = 0;     key->y = 0;     index1 = 0;     index2 = 0;   for(counter = 0; counter &lt; 256; counter++) {     index2 = (key_data_ptr[index1] + state[counter] +               index2) % 256;     swap_byte(&state[counter], &state[index2]);     index1 = (index1 + 1) % key_data_len;   } }  void rc4(unsigned char *buffer_ptr, int buffer_len, rc4_key         *key) {   unsigned char x, y, xorIndex;   unsigned char* state;   short counter;      x = key->x;     y = key->y;      state = &key->state[0];   for(counter = 0; counter &lt; buffer_len; counter ++) {     x = (x + 1) % 256;     y = (state[x] + y) % 256;     swap_byte(&state[x], &state[y]);     xorIndex = state[x] + (state[y]) % 256;     buffer_ptr[counter] ^= state[xorIndex];   }   key->x = x;     key->y = y; }

Listing 7-2: RC-4 code in C, from original Usenet posting.⁴

RC-4 is thought to be a strong cipher, although there are a few known weaknesses in the key scheduling algorithm that can be leveraged in poorly designed cryptosystems, such as WEP. Scott Fluhrer, Itsik Mantin, and Adi Shamir document these weaknesses in a paper titled “Weaknesses in the Key Scheduling Algorithm of RC4,” presented at the Eighth Annual Workshop on Selected Areas in Cryptography (August 2001). None of these weaknesses can be applied against the Xbox’s implementation of RC-4.

There is, however, a potential problem in the way that RC-4 is used in the first version of the Xbox security. RC-4 is used on the Xbox to encipher a stream of x86 code, and no significant check is performed on the deciphered code to ensure the integrity of the plaintext. This means that changes in the ciphertext wil lead to changes in the code that the Xbox executes. The trick is to figure out a change in the ciphertext that leads to a meaningful code modification. Since RC-4 encrypts one byte at a time and x86 opcodes can be as short as a single byte, it requires no more than 2⁸ = 256 iterations to “brute force” an instruction into a single known location by mutating the ciphertext.

Determing which location to brute force can be tricky, but I suspect a lot of information could be derived by mutating ciphertext bits and observing what happens to the pattern of instruction fetches, even with the caches turned on. The goal would be to try and identify the location of a jump opcode’s operands and to modify the jump destination such that the secured program jumps into an unsecured region of memory. The process would be similar to playing the classic board game “Battleship.” Keep in mind that the attack is so easy that guessing through a kilobyte of code only requires a maximum of 218 iterations. The guessing process could be automated by integrating a logic analyzer with a ROM emulator via a control script running on a host computer.

The history behind RC-4 is actually quite interesting. RC-4 was invented in 1987 by Ron Rivest, and was kept as a trade secret by RSA Security, Inc. until it was released in 1994 by an anonymous post to a cypherpunks mailing list (see Listing 7-2). As a result of RC-4’s virtues of simplicity and robustness, it has found its way into numerous applications, including WEP, SSL, SQL, and CDPD. While the source code for RC-4 is widely distributed and well known, the cipher is still the intellectual property of RSA Security. I wouldn’t recommend integrating it into a commercial product without first obtaining a license from RSA Security.

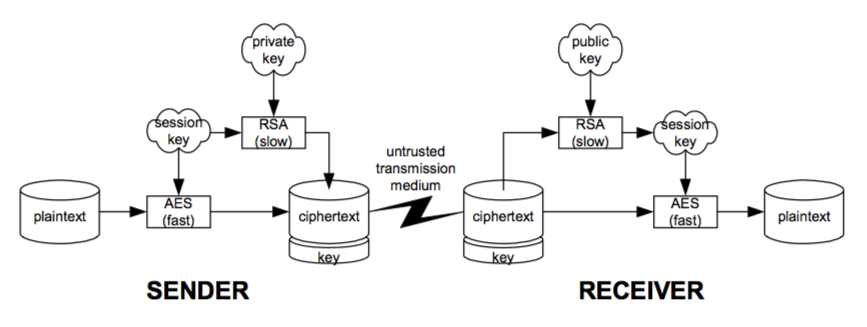
Figure 7-3: Use of RSA with session keys.

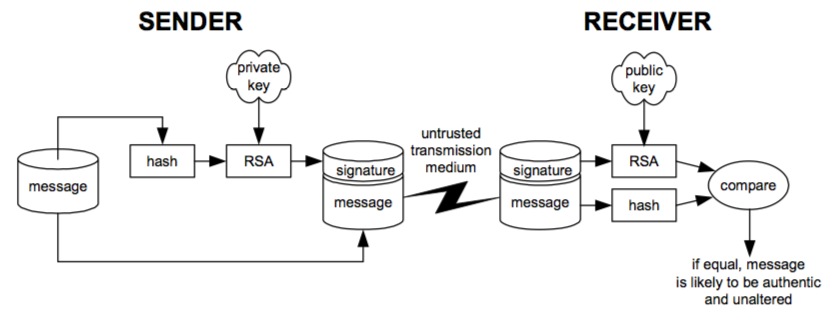
figure_7-4

Figure 7-4: RSA used to implement digital signatures.

RSA

RSA is a public-key algorithm devised by Ron Rivest, Adi Shamir and Leonard Adleman in 1977. In a public-key algorithm, two distinct keys are used, a public key and a private key. As their names imply, the private key must be kept secret, while the public key can be freely distributed. The math behind RSA is briefly described in the sidebar titled “The RSA Algorithm.” You need not understand the details of the math behind RSA to grasp how RSA is used in the context of the Xbox.

Brute-force attacks are currently thought to be infeasible on RSA with keylengths in excess of about a thousand bits. Also note that one cannot be too cavalier about how RSA is integrated into a cryptosystem. There are some attacks against protocols that use RSA, such as tricking the private key holder into signing carefully crafted messages that can then be used to derive the signer’s private key.

Encrypting a message using RSA is as simple as invoking RSA on a message. However, RSA encryption works on message blocks that are too short and the encryption process is too slow to be practical for most messages. Thus, RSA is typically used to encrypt a single-use random key, called a session key, for a fast symmetric cipher such as AES that is then used to encrypt the bulk message. This process is illustrated in Figure 7-3.

In addition to encryption, RSA enables digital signatures. A digital signature allows parties exchanging messages over an insecure medium to guarantee that messages are not forged and are not modified. The message does not have to be encrypted. A typical digital signature protocol works as follows: The sender computes a hash of the message to be sent. This hash is then encrypted with the sender’s private key and included with the message plaintext. The receiver decrypts the encrypted message hash using the sender’s public key, and compares this hash against a locally computed hash of the received message. If the decrypted hash sent with the message and the locally computed hash agree, then the receiver could conclude that the message is authentic and unaltered. This process is outlined in Figure 7-4.

The RSA Algorithm

The RSA algorithm was patented by the Massachusetts Institute of Technology and exclusively licensed to RSA Data Security, Inc in 1983. The patent on the RSA algorithm has since expired in September 2000. Thus, today RSA is free to use in any application. Many excellent tutorials and educational examples using RSA can now be found on the Internet. Perform a Google search using the keywords “RSA algorithm” to find some of these examples.

The RSA algorithm is as follows (adapted from http://world.std.com/~franl/crypto/rsa-guts.html):

1. Find two large (thousands of bits long) prime numbers, “P” and “Q”.

2. Choose “E” such that E > 1, E < PQ, and E is relatively prime to (P-1)(Q-1). E does not have to be prime, but it must be odd. The pair of E and PQ are the public key.

3. Compute “D” such that (DE - 1) is evenly divisible by (P-1)(Q-1). This can be accomplished by finding an integer X which causes D = (X(P-1)(Q-1) + 1)/E to be an integer. D is the private key.

4. Plaintext “T” is encrypted using the function

C = (T^E) mod PQ

5. Ciphertext “C” is decrypted using the function

T = (C^D) mod PQ

Note that T < PQ. Messages larger than PQ must be broken down into a sequence of smaller messages, and very short messages must be padded with carefully selected values to foil dictionary attacks, among other things.

If this protocol sounds complex to you, it is. There are a lot of places where things can go wrong. The receiver could have a false copy of the sender’s public key. The sender could have had his private key compromised. The hash could have weaknesses. Employing digital signatures in an adversarial environment requires attention to detail at all levels of the system design.

In the Xbox, digital signatures are used to control the distribution and sale of programs for the console. Microsoft is effectively in control of both the sender and the receiver of messages. The receivers — Xbox consoles — are programmed to only run programs that are digitally signed by Microsoft. In an ideal world, this guarantees that Microsoft has the final word on who can or cannot run programs on the console, and hackers cannot modify games to insert viruses, Trojan horses, or back doors. Saved games are also sealed using encryption, and as a result, it is nominally impossible to hack a game and cheat by patching the executable or by jacking up your character stats.

Clearly, a pivotal issue in hacking the Xbox console is their implementation of the digital signature system. The Xbox uses a SHA-1 hash with 2048-bit RSA keys, making the chance of a successful brute force attack very, very slim. Of course, the probability is zero if you never try, but the odds are stacked against you (see the sidebar “Very Difficult Problems”). You’ll have better luck trying to win the lottery. This is by no mistake; the discovery of the private key would make game copying trivial and developers would not have to pay royalties to Microsoft (legally, they may be obligated but there is no technical reason preventing them). Given that this key is probably worth a few billion dollars to Microsoft, it is quite likely that no single human knows the full key, as rubber-hose (beatings) and green-paper (bribery) cryptanalysis techniques tend to be quite effective on humans. (Do not discount real “brute force” as a possibility if you are trying to protect an extremely valuable secret!) Products such as BBN’s SignAssure™ certificate authority management system ensure the physical security of high-value keys and implement secret-sharing schemes that require multiple trusted users to activate the machine.

As mentioned previously, there are a few known viable attacks against RSA, but not all of them apply in the Xbox scenario, as they rely on groups of users or require chosen-ciphertext. In addition, the list of weaknesses is widely known and most implementations of digital signatures implement the proper countermeasures to protect against such attacks.

The Rest of the Picture

An effective security system needs good key management, strong protocols, and in the case of the Xbox, physical security in addition to strong ciphers and hashes.

Key management is perhaps one of the most difficult system implementation tasks that face any security architect. Ultimately, the decryption keys need to go into the hands of a user. The user interface must be designed so that the average user with minimum training does not accidentally leak key information. As ciphers become stronger, the easiest path of attack is increasingly through the user. Eavesdropping through surveillance videos, social engineering, or even analyzing the pattern of sounds made by the keyboard as a password is typed will probably yield more information per unit effort about a passphrase than cryptanalysis. Public key cryptography partially helps solve the problem of key distribution, but public key fingerprints should be compared in person to rule out the possibility of man-in-the-middle attacks. Public key cryptography also does not prevent someone with physical access to the client machine from eaves dropping on the decrypted output.

In addition, protocol attacks find weaknesses in the way keys and data are manipulated, or in the way strong ciphers are used. The WEP attack on RC-4 and Mike Bond and Ross Anderson’s attack on the IBM 4758 Cryptoprocessor are both examples of protocol attacks. The red flags for potential protocol attacks are systems that implement backward-compatibility measures, and systems that are implemented by engineers whose primary job is not crypto-security.

Finally, in a system like the Xbox where one of the goals is to establish a trustable client, back doors and buffer-overrun attacks are also viable attacks on the trust state of a machine. No widely used commercial processors embed execution privileges within instruction streams or data tags. Processors blindly execute any piece of code that it is instructed to jump to, whether or not the jump was induced through a transient hardware failure or through maliciously placed code. Periodic hashes on the machine state can be used to counter this deficiency, but even then the state checks can be spoofed.

As discussed in the beginning of this chapter, establishing the trust state of a client also requires a piece of tamper-resistant hardware to carry the seed of trust. The amount of physical security must be enough to make it uneconomical to defeat the security once, and robust enough such that one instance of broken security does not enable trivial attacks on the remainder of the consoles. Some of the trade-offs when designing physical security as well as the decisions made by Microsoft to this end are discussed in the next chapter.

The moral of this chapter is that security requires a well-designed system. Although ciphers have become strong enough to make brute-force attacks moot, systems have grown in complexity. This complexity increases the likelihood of a viable protocol or back door attack, yet does little to save users from the more traditional eavesdropping, rubber-hose and user-error attacks.

¹ http://interviews.slashdot.org/article.pl?sid=03/02/04/2233250&mode=nocomment&tid=103&tid=123&tid=172

² Merriam-Webster OnLine Dictionary (www.webster.com).

³ Code is from http://vader.brad.ac.uk/tea/source.shtml#ansi

⁴ Code from http://www.cc.jyu.fi/~paasivir/crypt/rciv/rc4article.txt. Minor white-space modifications to make it all fit on one page. The swap byte function definition is also not included, but you can guess what it does by its name.