ГЛАВА 16
ОДНОСТОРОННЯЯ ИСТОРИЯ
В эпизоде «Мебиус Дик» космический корабль «Межпланетный экспресс» путешествует по галактике и случайно попадает в Бермудский тетраэдр, космическое кладбище десятков знаменитых исчезнувших кораблей. Экипаж «Межпланетного экспресса» решает исследовать эту область пространства, но тут на них нападает внушающий ужас четырехмерный космический кит, которому Лила дает имя Мебиус Дик.
В этом имени содержится как ссылка на роман Германа Мелвилла «Моби Дик», так и на удивительный математический объект, известный как лента Мебиуса, или петля Мебиуса. Ленту Мебиуса независимо друг от друга открыли в XIX столетии немецкие математики Август Мебиус и Иоганн Листинг. Воспользовавшись следующими простыми инструкциями, вы сами можете построить такую ленту. Вам понадобится:
1) полоска бумаги;
2) скотч.
Сначала возьмите полоску бумаги и переверните ее на пол-оборота, как показано на рисунке ниже. Затем склейте два конца полоски скотчем, чтобы получить ленту Мебиуса. Вот и все. Лента Мебиуса — это, по сути, петля с поворотом.
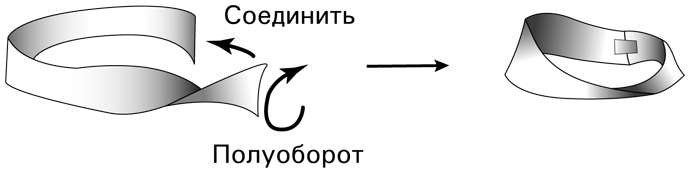
На первый взгляд в ленте Мебиуса нет ничего особенного, но простой эксперимент позволяет раскрыть одно ее удивительное свойство. Возьмите маркер и нарисуйте линию вдоль ленты, не отрывая кончик маркера от бумаги и не пересекая край, до тех пор пока не вернетесь в исходную точку. Вы заметите две вещи: во-первых, для того чтобы вернуться в исходную точку, вам понадобится пройти два круга; во-вторых, ваша линия пройдет по каждой стороне ленты. Это очень странно, поскольку мы исходим из предположения, что у листа бумаги две стороны, на которых можно нарисовать линию только тогда, когда вы можете оторвать перо от бумаги или обогнуть край. Так что же происходит в случае ленты Мебиуса?
Лист бумаги имеет две стороны (верхнюю и нижнюю), и сделанная из бумаги петля также имеет две стороны, но лента Мебиуса отличается наличием одного необычного свойства: у нее только одна сторона. Две стороны исходной полоски бумаги превратились в одну после того, как один конец полоски был перевернут перед соединением. Это необычное свойство ленты Мебиуса лежит в основе моей третьей любимой математической шутки:
Вопрос: Зачем цыпленок перешел ленту Мебиуса?
Ответ: Чтобы попасть на другую сторону… ну… в общем…
Хотя на самом деле мы не видим ленту Мебиуса в эпизоде «Мебиус Дик», это весьма прозрачный намек на планы включить эту необычную математическую шутку в следующий эпизод «Футурамы». Когда я осенью 2012 года встречался с Дэвидом Х. Коэном в офисе «Футурамы», он рассказал мне об одном из эпизодов следующего сезона под названием «Двумерное шоссе» (2-D Blacktop), в котором главную роль играет профессор Фарнсворт. Коэн объяснил, что по сюжету эпизода пожилой владелец компании «Межпланетный экспресс» превращается в помешанного на скорости типа, который увеличивает мощность двигателя космического корабля для того, чтобы принять участие в гонках по гоночной ленте Мебиуса. Интересное свойство такого маршрута состоит в том, что Фарнсворту понадобится пройти два круга, прежде чем он сможет попасть в исходную точку.
Коэн раскрыл несколько деталей сюжета: «Лила злится на профессора, и между ними возникает спор, который заканчивается гонкой по ленте Мебиуса. Лила выигрывает, но у профессора в запасе есть отличный гоночный ход под названием “дрифт между измерениями”. Фарнсворт выкручивает руль, одновременно задействуя аварийный тормоз, что выбрасывает его в пространство, в котором на одно измерение больше, чем было раньше. Так он вылетает из третьего измерения, на какое-то время попадает в четвертое, а затем снова появляется в третьем измерении дальше по трассе».
К сожалению, переход из одного измерения в другое и обратно приводит к тому, что профессор теперь движется в направлении, противоположном направлению движения Лилы. Их корабли сталкиваются друг с другом, из-за чего попадают во второе измерение! Следующая сцена происходит в двумерном пространстве.
Во многих отношениях сюжет эпизода «Двумерное шоссе» противоположен сюжету «Трехмерного Гомера». В эпизоде «Симпсонов» речь идет о последствиях перехода в более высокое измерение, по аналогии с сюжетом одного из эпизодов сериала «Сумеречная зона». Напротив, в «Двумерном шоссе» исследуются последствия перехода в пространство меньшей размерности, причем этот сюжет также написан под влиянием классического произведения в жанре научной фантастики.
Сюжет эпизода «Двумерное шоссе» — дань уважения научно-фантастическому роману Эдвина Эббота под названием Flatland (подзаголовок «Роман о многих измерениях»). Действие начинается в двумерном мире, известном как Флатландия. Этот мир состоит из единственной поверхности, населенной различными фигурами, такими как сегменты линий (женщины), треугольники (мужчины рабочего класса) и квадраты (мужчины среднего класса). По сути, чем больше количество сторон у фигуры, тем выше ее статус. Следовательно, у женщин в этом мире самый низкий статус, многоугольники представляют высшие слои общества, а окружности — это верховные жрецы. Будучи теологом, изучавшим математику в Кембриджском университете, Эббот стремился к тому, чтобы читатели воспринимали его «Флатландию» и как социальную сатиру, и как приключения в мире геометрии.
Главный герой и рассказчик — Квадрат, которому снится сон о путешествии в Лайнландию, одномерный мир, обитатели которого (точки) могут перемещаться только по одной линии. Квадрат беседует с точками и пытается объяснить им концепцию второго измерения, а также разнообразие фигур, населяющих Флатландию, но точки остаются в недоумении. Они даже не могут понять истинную природу самого Квадрата, поскольку его форма непостижима с их одномерной точки зрения. Точки видят Квадрат в форме линии, так как это и есть то сечение, которое образует квадрат, перемещаясь по Лайнландии.
После того как Квадрат просыпается и понимает, что снова находится в своей родной Флатландии, его приключения продолжаются после посещения Сферы — объекта из экзотического третьего измерения. Безусловно, в этот раз именно Квадрат сбит с толку, поскольку он может воспринимать Сферу только как окружность, ведь именно такую форму имеет сечение, образуемое Сферой при перемещении по Флатландии. Однако происходящее начинает обретать смысл, когда Сфера переносит Квадрат в трехмерное пространство. Когда Квадрат смотрит из третьего измерения вниз на своих земляков, обитающих в Флатландии, он уже может рассуждать о четвертом, пятом и даже более высоких измерениях.
Вернувшись во Флатландию, Квадрат пытается всем рассказать о третьем измерении, но никто не желает его слушать. Более того, власти стремятся прекратить это богохульство. На самом деле лидеры Флатландии уже знают о существовании Сферы, поэтому берут Квадрата под арест, с тем чтобы сохранить информацию о третьем измерении в тайне. У этой истории трагический конец: Квадрата сажают в тюрьму за то, что он сказал правду.
Так каким же образом эпизод «Двумерное шоссе» воздает должное роману «Флатландия»? Когда корабли профессора Фарнсворта и Лилы сталкиваются, в результате прямого удара они превращаются в плоские версии себя и перемещаются в плоском мире с плоскими животными, растениями и облаками.
Анимация в этом фрагменте эпизода строго придерживается правил двумерного мира, а это значит, что ни один объект не может перемещаться мимо другого объекта; в таком мире они могут только обходить друг друга. Однако когда я смотрел предварительный монтаж этих кадров вместе с редактором Полом Колдером, он заметил, что пушистый край одного облака слегка накладывается на край другого облака. В двумерном мире такое наложение невозможно, поэтому этот фрагмент необходимо подкорректировать, прежде чем эпизод выйдет на экраны.
Пытаясь понять последствия пребывания в новом мире, Лила и профессор постепенно осознают, что при переходе из третьего во второе измерение у них исчезли каналы пищеварительной системы. Это необходимая часть процесса перехода, поскольку пищеварительный канал в двух измерениях — верный путь к беде. Для того чтобы понять суть проблемы, представьте себе профессора в виде плоской, вырезанной из бумаги фигуры, повернутой лицом направо. Затем проведите линию от рта до ягодиц, символизирующую желудочно-кишечный канал. И наконец, разрежьте фигуру вдоль этой линии и слегка отодвиньте две части тела профессора друг от друга: пищеварительный канал представляет собой трехмерный тоннель, но в двух измерениях это просто щель. Теперь вы видите, в чем проблема. При наличии пищеварительной системы в двумерном пространстве тело профессора просто распалось бы на две части. Очевидно, что то же самое произошло бы и с Лилой.
Однако без пищеварительного тракта профессор и Лила не могут есть. Другие обитатели двумерного мира каким-то образом впитывают питательные вещества, в отличие от поглощения пищи и выделения продуктов ее переработки, но профессор и Лила не умеют этого делать.
Короче говоря, для профессора и Лилы сложилась ситуация, когда и с пищеварительным трактом не выжить, и без него не жить. Единственный выход — бежать из двумерного мира, пока они не умерли голодной смертью. К счастью, им на помощь приходят сценаристы. Коэн объясняет это так: «Профессор и Лила поняли, что происходит. Они могут использовать дрифт между измерениями, чтобы переместиться из второго в третье измерение. И здесь появляется удивительная последовательность кадров, когда они пролетают сквозь огромный фрактальный ландшафт, представляющий собой область между вторым и третьим измерением. Эта сцена содержит фрагмент поразительной компьютерной графики».
Фрактальный ландшафт в данной ситуации особенно уместен, поскольку фракталы как раз и демонстрируют фрактальную (дробную) размерность. Фрактальный ландшафт появляется в процессе перемещения из двумерного в трехмерный мир; именно здесь и можно рассчитывать на присутствие дробной размерности.
Если вы хотите узнать о фракталах больше, прочитайте , в котором приведен краткий обзор этой темы и уделяется особое внимание тому, как объект может быть представлен в виде фрактальной размерности.
* * *
Лента Мебиуса из «Двумерного шоссе» перекликается с математической концепцией, присутствующей в эпизоде «Путь всех зол» (The Route of All Evil, сезон 3, эпизод 12; 2002 год). Во второстепенной сюжетной линии эпизода рассказывается о том, что Бендер превращает себя в пивоварню. Идея возникает у него после посещения магазина 711, куда он с коллегами по «Межпланетному экспрессу» заходит за выпивкой. В магазине есть напиток, который обычно пьет Бедер, — пиво Olde Fortran, названное так в честь разработанного в 1950-х годах языка программирования FORTRAN (сокр. от FORmula TRANslation — «перевод формул»). Кроме того, на полках также выставлено пиво St. Pauli’s Exclusion Principle Girl («Эксклюзивная девушка настоятеля святого Паули), в названии которого присутствует ссылка на реальное пиво St. Pauli Girl, а также на один из фундаментальных законов квантовой физики — принцип исключения Паули. Самый большой интерес представляет третий сорт пива — Klein’s, которое разлито в бутылки странной формы. Истинные ценители необычных геометрических фигур узнают в ней бутылку Клейна, которая тесно связана с лентой Мебиуса.
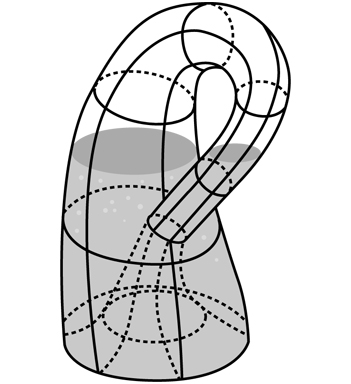
Эта фигура названа в честь Феликса Клейна, одного из величайших немецких математиков XIX столетия. По всей вероятности, судьба Клейна была предопределена еще в момент его появления на свет, поскольку каждый элемент даты его рождения (25 апреля 1849 года) представляет собой квадрат простого числа:
Апрель | 25 | 1849 |
4 | 25 | 1849 |
22 | 52 | 432 |
Клейн занимался исследованиями в разных областях, но самой знаменитой является его так называемая бутылка Клейна. Как и в случае ленты Мебиуса, вам будет легче понять форму и структуру бутылки Клейна, если вы сами сконструируете ее модель. Вам понадобятся:
1) лист резины;
2) скотч;
3) четвертое измерение.
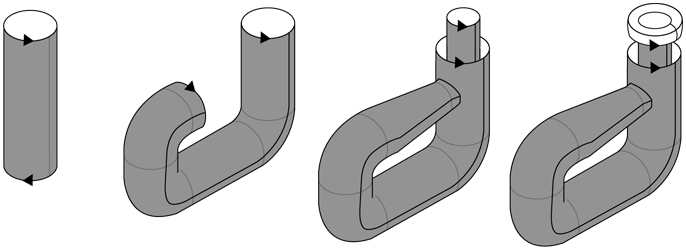
Если у вас, так же как и у меня, нет доступа к четвертому измерению, тогда попробуйте себе представить, как теоретически построить псевдобутылку Клейна в трех измерениях. Сначала представьте, что вы скручиваете лист резины в цилиндр и склеиваете его скотчем по длине, как показано на первом рисунке ниже. Затем отметьте два конца цилиндра стрелками, указывающими в противоположных направлениях. Далее (и это самый сложный этап) цилиндр необходимо изогнуть таким образом, чтобы можно было соединить два его конца со стрелками, указывающими в одном направлении.
Именно здесь пригодилось бы четвертое измерение, но вместо этого вам придется проявить смекалку. Как показано на двух средних рисунках, необходимо изогнуть цилиндр, а затем представить себе, что вы просовываете один его конец через отверстие в его же стенке и разворачиваете его внутри вверх. И наконец, после этого самопересечения заверните выступающий конец цилиндра вниз (как показано на четвертом рисунке), для того чтобы соединить два конца цилиндра. Важно, чтобы после такого соединения стрелки на каждом конце цилиндра указывали в одном направлении.
И бутылка Клейна, и бутылка пива Klein’s в «Футураме» — это самопересекающиеся фигуры, поскольку они существуют в трехмерном пространстве. Напротив, в четырехмерном мире бутылке Клейна нет необходимости пересекаться с самой собой. Для того чтобы объяснить, как дополнительное измерение позволяет избежать самопересечения, давайте рассмотрим аналогичную ситуацию с участием меньшего количества измерений.
Вообразите фигуру в форме восьмерки, нарисованную ручкой на бумаге. В этом случае чернильная линия неизбежно пересечет сама себя в центре восьмерки, подобно тому как цилиндр пересекает сам себя посредине бутылки Клейна. Такое пересечение имеет место потому, что линия расположена в двумерной плоскости. Однако эта проблема не возникнет, если добавить третье измерение и сделать восьмерку из куска веревки. Один ее фрагмент можно поднять в третье измерение, поскольку он накрывает второй фрагмент веревки, а значит, ей нет необходимости пересекаться с самой собой. Следовательно, если бы цилиндр из резинового листа можно было переместить в четвертое измерение, то появилась бы возможность сконструировать бутылку Клейна без самопересечения.
Еще один способ понять, почему бутылка Клейна пересекает сама себя в трехмерном пространстве, но не пересекает в четырехмерном, сводится к сравнению нашего восприятия ветряной мельницы в трех и двух измерениях. В трехмерном измерении мы видим, как лопасти ветряной мельницы вращаются перед вертикальной башней. Однако ситуация меняется, если взглянуть на тень ветряной мельницы на траве. В этом двумерном представлении лопасти как будто проносятся сквозь башню снова и снова. В двумерной проекции они пересекают башню, чего не происходит в трехмерном мире.
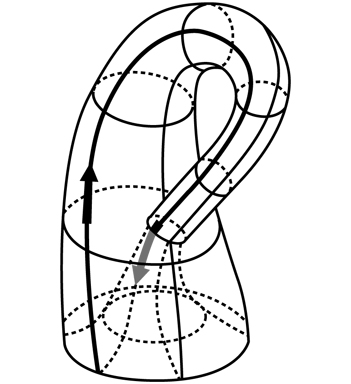
Очевидно, что форма бутылки Клейна отличается от формы обычной бутылки, что, в свою очередь, указывает на одно удивительное свойство бутылки Клейна, которое становится очевидным, если мы представим, что перемещаемся по поверхности бутылки Клейна, как показано на рисунке ниже. В частности, вообразите, что вы движетесь в направлении, которое указывает черная стрелка, расположенная на внешней поверхности бутылки Клейна.
Стрелка перемещается вверх, затем поворачивает вокруг внешней поверхности горлышка бутылки и уходит за точку пересечения, где конец стрелки становится серым. Это говорит о том, что теперь она проходит по внутренней поверхности бутылки. Переместившись вперед, стрелка возвращается в исходную точку, за исключением того, что теперь она находится внутри бутылки. Если стрелка продолжит свое путешествие вверх, к горлышку бутылки, и снова вниз, к основанию, то она вернется на внешнюю поверхность и в конце концов выйдет на исходную позицию. То, что стрелка может без отрыва перемещаться между внутренней и внешней поверхностью бутылки Клейна, означает, что на самом деле обе поверхности представляют собой фрагменты одной и той же поверхности.
Безусловно, без четко выраженной внутренней и внешней поверхности бутылка Клейна не отвечает основным критериям, по которым ее можно бы было считать бутылкой в привычном понимании. В конце концов, как можно налить пиво в бутылку, у которой внутри — это то же самое, что снаружи?
В действительности Клейн никогда не называл свое творение бутылкой. Первоначально этот объект обозначался термином Kleinsche Fläche («поверхность Клейна»), что вполне уместно, поскольку он состоит из одной поверхности. Однако англоязычные математики, по всей вероятности, неправильно перевели этот термин, прочитав его как Kleinsche Flasche, что означает «бутылка Клейна» — и это название прижилось.
И наконец, вернемся к вопросу, который уже поднимался выше: бутылка Клейна и лента Мебиуса тесно связаны друг с другом. Самая очевидная связь заключается в том, что у них есть одно любопытное свойство: у обеих только одна поверхность. Вторая (хотя и менее очевидная) связь состоит в том, что бутылка Клейна, разрезанная на две половины, образует пару лент Мебиуса.
К сожалению, вы не сможете выполнить этот трюк, потому что бутылку Клейна можно разрезать только в случае доступа к четырехмерному пространству. Однако вы можете разрезать ленту Мебиуса. На самом деле я бы даже рекомендовал вам разрезать ее по длине, чтобы посмотреть, что получится в результате.
Если вам понравилось разрезать ленты, вот вам еще одна идея для вашего нового хобби — геометрической хирургии. Сделайте ленту, перевернув ее на 360 градусов (а не на пол-оборота, как в ленте Мебиуса). Что произойдет, если разрезать ее вдоль? Для того чтобы понять столь изощренное рассечение, понадобится изощренный ум.

