ГЛАВА 15
ЧИСЛО 1729 И РОМАНТИЧЕСКОЕ ПРОИСШЕСТВИЕ
Герой «Футурамы» Зепп Бранниган — это 25-звездный генерал и капитан звездолета «Нимбус». Хотя у Браннигана много восторженных поклонников, считающих его храбрым воином, в действительности он одержал большинство побед в борьбе против более слабых соперников, таких как пацифисты из Туманности Ганди или пенсионеры из Туманности пожилых людей. Бранниган — по сути своей позер, тщеславие и невежество которого вызывают раздражение у членов его экипажа. В действительности терпеливый помощник Браннигана лейтенант Киф Крокер изо всех сил старается скрыть свое презрение к некомпетентному руководителю.
Киф — обитатель планеты Амфибиус 9, появление которого в эпизодах «Футурамы» зачастую связано с его сложными отношениями с Бранниганом или романтическими — со стажером «Межпланетного Экспресса» Эми Вонг. Всякий раз, когда Киф и Эми оказываются в одной области Вселенной, они делают все возможное, чтобы встретиться и провести немного времени вместе. В эпизоде «Киф, похоже, залетел» (Kif Gets Knocked Up a Notch, сезон 4, эпизод 1; 2003 год) Эми посещает Кифа на борту «Нимбуса», где Киф ведет ее в голозал, который используется для моделирования реальности посредством проецирования трехмерных голографических изображений различных объектов и существ. Эми визжит от радости, когда в голозале появляется знакомое ей животное.
Эми. Спирит! Киф, я всегда мечтала об этом пони, но родители сказали, что у меня и так их слишком много.
Киф. Да, я запрограммировал его для тебя. Четыре миллиона команд на Бейсике!
В эпизоде «Я, сосед» мы уже встречались с шуткой, в основу которой положено знание языка программирования Бейсик. Хотя ссылки на компьютерные науки — традиция «Футурамы», один из сценаристов сериала, не принадлежащий к числу нердов, не оценил строку диалога с упоминанием о четырех миллионах команд на Бейсике. Он посчитал эту шутку слишком трудной для понимания и предложил ее удалить. Но Эрик Каплан (сценарист, который изучал в свое время философию науки) сразу же отверг эту идею. Патрик Веррон, присутствовавший тогда на совещании, вспоминает об этом так: «Эрик Каплан высказал там знаменитое замечание. Кто-то сказал: “Четыре миллиона команд на Бейсике — кто это поймет?” И Каплан в сердцах выпалил: “Да ну их к черту!” С тех пор это стало мантрой. Если зрители не понимают чего-то, они получат следующую шутку».
В том же эпизоде есть еще более непонятная математическая ссылка, находящаяся на боковой стороне космического корабля «Нимбус». Проницательные фанаты «Футурамы» обязательно заметят, что регистрационный номер корабля — BP-1729. Было бы проще всего проигнорировать этот номер, считая его произвольным числом, но сценаристы «Футурамы» никогда не упускают случая воздать должное математике, поэтому было бы правильнее исходить из предположения, что каждое число появляется на экране неспроста.
На самом деле число 1729 должно иметь определенный смысл, так как оно возникает в различных ситуациях в нескольких эпизодах «Футурамы». Например, в эпизоде «Рождественская история» (Xmas Story, сезон 2, эпизод 4; 1999 год) появляется Мамочка, коварная владелица компаний MomCorp и Mom’s Friendly Robot Company. Учитывая, что Мамочке принадлежит завод, построивший Бендера, она считает себя его матерью, поэтому присылает ему открытку с серийным номером:

Кроме того, в эпизоде «Парабокс Фарнсворта» (The Farnsworth Parabox, сезон 4, эпизод 15; 2003 год) экипаж «Межпланетного экспресса» втягивается в авантюру с параллельными вселенными, причем каждая вселенная заключена в коробку с определенным номером. Проверяя коробки в поисках своей вселенной, Фрай запрыгивает в одну из них и оказывается во вселенной 1729.
Так что же делает число 1729 таким особенным? Может, оно появляется в различных эпизодах «Футурамы» по той причине, что указывает на особый фрагмент числа е? Если мы точно определим 1729-й десятичный знак числа е, то увидим, что с него начинается первая последовательность всех десяти цифр в этом знаменитом иррациональном числе:

Однако кто-то наверняка посчитает это наблюдение тривиальным, тогда, может, это одно из чисел харшад — категории чисел, которую выделил авторитетный индийский математик и школьный учитель Даттатрея Рамчандра Капрекар (1905–1986). На древнеиндийском языке санскрит слово «харшад» означает «даритель радости», а ее причина в том, что такие числа без остатка делятся на сумму своих цифр. Следовательно, если мы сложим цифры числа 1729, то получим 1 + 7 + 2 + 9 = 19, а 1729 действительно делится на 19 без остатка.
Кроме того, 1729 — особое число харшад, так как оно является результатом умножения суммы своих цифр на число, обратное этой сумме: 19 × 91 = 1729. Это делает данное число примечательным, но не уникальным, потому что есть еще три числа с аналогичным свойством: 1, 81 и 1458. Но поскольку авторы «Футурамы» не одержимы числами 1, 81 или 1458, должна быть другая причина того, почему число 1729 неоднократно появляется в сценариях к разным эпизодам мультсериала.
На самом деле сценаристы выбрали число 1729 в качестве регистрационного номера звездолета «Нимбус», серийного номера Бендера и номера параллельной вселенной потому, что оно упоминается в одной из самых знаменитых бесед за всю историю математики, которая состоялась в конце 1918 — начале 1919 года между двумя величайшими математиками ХХ столетия, Годфри Харди и Шринивасой Рамануджаном. Трудно даже себе представить, что у двух людей с такими разными биографиями столько общего.
Годфри Харолд Харди (1877–1947) вырос в семье учителей в графстве Суррей (Англия). В двухлетнем возрасте он записывал числа, достигающие миллионов, а чуть позже вычислял делители чисел из церковных гимнов, чтобы немного развлечься во время церковных служб. Харди получил стипендию для обучения в престижном Уинчестерском колледже, а затем учился в Тринити-колледже Оксфордского университета, где стал членом тайного общества под названием «Кембриджские апостолы». К тридцати годам Харди уже был одним из немногих британских математиков мирового уровня. На самом деле в начале ХХ столетия французы и немцы (среди прочих) превзошли британцев в плане математической строгости и амбиций, но исследования и лидерские качества Харди помогли восстановить репутацию страны в этой области. Всего этого уже было достаточно для того, чтобы Харди занял достойное место среди великих математиков, но он сделал еще более весомый вклад, открыв талант гениального юноши по имени Шриниваса Рамануджан, которого считал самым одаренным математиком современной эпохи.
Шриниваса Рамануджан родился в 1887 году в южном индийском штате Тамил-Наду. В возрасте двух лет он заболел оспой, но выжил, в отличие от троих младших братьев и сестер, которые умерли в младенческом возрасте. Бедные родители посвятили всю свою жизнь единственному ребенку и записали его в местную школу. Со временем школьные учителя начали замечать, что Рамануджан демонстрирует поразительные способности к математике и порой даже ставит их в тупик. Интерес Рамануджана к математике в значительной мере связан с тем, что однажды в библиотеке он наткнулся на книгу Джорджа Шубриджа Карра A Synopsis of Elementary Results in Pure Mathematics («Сборник элементарных результатов чистой математики»), в которой были собраны доказательства тысяч теорем. Мальчик анализировал эти теоремы и методы их доказательства, но ему приходилось выполнять громоздкие вычисления с помощью мела и грифельной доски, используя загрубевшие локти в качестве ластика, поскольку он не мог позволить себе бумагу.
Единственный недостаток такой одержимости математикой состоял в том, что Рамануджан пренебрегал другими предметами. В итоге, когда пришло время сдавать экзамены, Рамануджан получил плохие оценки, из-за чего индийские колледжи отказали ему в предоставлении стипендии, необходимой для продолжения учебы. В итоге Рамануджан нашел работу клерка и пополнял свой скудный доход за счет преподавания математики студентам. Парень отчаянно нуждался в дополнительном доходе, после того как в 1909 году женился (ему исполнился тогда двадцать один год, а его невесте Джанакиаммал — всего десять).
В тот период Рамануджан в свободное от работы время начал развивать новые математические идеи. Он чувствовал, что они важные, но ему не к кому было обратиться за советом и поддержкой. В отчаянном стремлении глубже изучить математику и получить признание Рамануджан стал писать английским математикам в надежде на то, что кто-то из них согласится быть его наставником или хотя бы выскажет свое мнение по поводу открытых им теорем.
Одна партия писем дошла в конце концов до Микая Джона Мюллера Хилла из Университетского колледжа Лондона. Содержание писем произвело на Хилла определенное впечатление, но он сделал молодому индийцу замечание по поводу применения устаревших методов и элементарных ошибок. Хилл в менторском тоне написал, что работы Рамануджана должны быть на понятном языке и без ошибок, а также что он не должен использовать символы, которых не может объяснить. Хотя это была безжалостная оценка, но по крайней мере Хилл ответил, в отличие от Генри Фредерика Бейкера и Эрнеста Уильяма Хобсона, вернувших работы Рамануджана без каких-либо комментариев.
В 1913 году Рамануджан написал письмо Годфри Харди, в котором объяснял: «У меня нет университетского образования, но я прошел обычный школьный курс. После окончания школы я использовал свободное от работы время для занятий математикой. Я не изучал традиционный официальный курс, предшествующий университетскому курсу, но я прокладываю для себя новый путь».
Когда пришло второе письмо, Харди обнаружил, что Рамануджан прислал ему в общей сложности 120 теорем для анализа. Молодой индийский гений впоследствии рассказывал, что многие из этих теорем ему нашептывала во сне Намагири, воплощение индийской богини Лакшми: «Во сне со мной произошло нечто необычное. Там был экран, как будто сделанный из текущей крови. Я смотрел на него. Вдруг какая-то рука начала на нем писать. Я внимательно следил за происходящим. Эта рука написала несколько эллиптических интегралов. Я их запомнил и записал сразу же после того, как проснулся».
Когда Харди углубился в работы Рамануджана, его оценка менялась от «мошенничества» до «гениальности настолько редкой, что в это трудно поверить». В итоге он пришел к выводу, что эти теоремы «должны соответствовать истине, поскольку если бы это было не так, ни у кого не хватило бы воображения их придумать». Харди называл Рамануджана «математиком высочайшего качества, человеком исключительной оригинальности и силы». В конечном счете он начал готовить почву для того, чтобы 26-летний Рамануджан приехал в Кембридж. Харди очень гордился тем, что стал человеком, который спас столь редкостный талант, и впоследствии называл это одним из самых романтических происшествий в своей жизни.
В апреле 1914 года два великих математика наконец встретились и совместно сделали ряд открытий в нескольких областях математики. В частности, они внесли большой вклад в изучение такой математической операции, как разбиение. Как следует из названия, операция разбиения сводится к разделению совокупности объектов на отдельные группы. Ключевой вопрос: сколько способов разбиения существует для заданного количества объектов? На представленном ниже рисунке показано, что есть только один способ разбиения одного объекта, но для группы из четырех объектов таких способов уже пять.
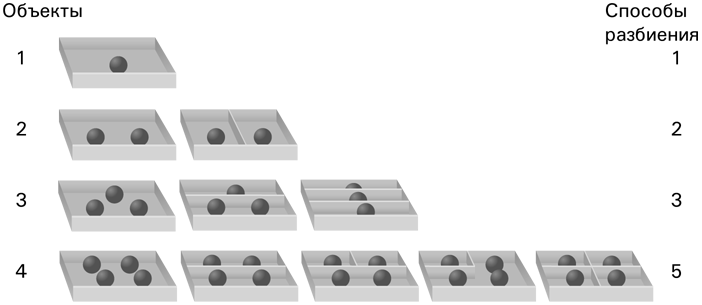
В случае небольшого количества объектов найти способы их разбиения не составляет труда, но по мере увеличения числа объектов уровень сложности задачи повышается. Это объясняется тем, что количество возможных вариантов разбиения стремительно увеличивается без какой-либо закономерности. Десять объектов можно разделить всего 41 способами, для 100 объектов существует уже 190 569 292 способов, а в случае 1000 объектов получается поразительное количество способов разбиения — 24 061 467 864 032 622 473 692 149 727 991.
Настоящим прорывом стало создание Харди и Рамануджаном формулы для определения количества способов разбиения очень большого числа объектов. Так как эта формула требует трудоемких вычислений, Харди и Рамануджан придумали также приближенную формулу, позволяющую получить хорошую оценку количества способов разбиения любого заданного числа объектов. Кроме того, Рамануджан сделал очень интересное наблюдение, которое до сих пор будоражит умы ученых: если число объектов заканчивается цифрой 4 или 9, то количество способов разбиения всегда делится на 5. В качестве иллюстрации этого утверждения можно привести такой пример: 4, 9, 14, 19, 24 и 29 объектов дают 5, 30, 135, 490, 1575 и 4565 способов разбиения соответственно.
Рамануджан добился многочисленных, сложных и блестящих достижений, а его гениальность получила признание в 1918 году, когда он был избран самым молодым членом Королевского общества. Переезд в Кембридж позволил разуму Рамануджана пережить невероятный расцвет, а вот суровая английская зима и изменение рациона питания негативно сказались на его здоровье. В конце 1918 года Рамануджан покинул Кембридж и лег в частную лечебницу Colinette House в пригороде Лондона Патни. Именно в этих условиях и состоялась та самая беседа, которая связывает Рамануджана с «Футурамой».
Вот что говорил об этом Харди: «Помню, как я однажды отправился проведать его в Патни. Я приехал на такси с номером 1729 и заметил, что это число кажется мне довольно скучным и что я надеюсь, в нем нет никакого плохого предзнаменования. “Нет, — ответил он, — это очень интересное число; это наименьшее число, которое можно представить в виде суммы кубов двумя разными способами”».
Эти двое явно не относились к любителям светской болтовни и сплетен. Как всегда, их разговор был посвящен числам, а его суть можно выразить так:
1729 = 13 + 123
= 93 + 103
Другими словами, если бы у нас было 1729 маленьких кубиков, мы могли бы сложить их в виде двух кубов со сторонами 1 × 1 × 1 и 12 × 12 × 12 или 9 × 9 × 9 и 10 × 10 × 10. Только немногие числа можно разделить на два куба, и еще меньше чисел, которые можно разделить на два куба двумя разными способами…, а число 1729 — минимальное число с таким свойством. В честь комментария Рамануджана по поводу номера такси, в котором ехал Харди, в математических кругах это число принято называть «числом такси».
Импровизированное замечание Рамануджана пробудило у математиков такой интерес, что они поставили вопрос несколько иначе: чему равно минимальное число, которое можно представить в виде суммы двух кубов тремя разными способами? Ответ — 87 539 319, поскольку:
87539319 | = | 1673 + 4363 |
| = | 2283 + 4233 |
| = | 2553 + 4143 |
Это число, которое тоже называют числом такси, присутствует в полнометражном мультфильме «Большой куш Бендера» (Bender’s Big Score, 2007 год). Когда Фрай вызывает такси, на его крыше красуется номер 87 539 319. Безусловно, это вполне естественно, когда в качестве номера такси (в обычном смысле) выступает число такси (в математическом смысле).
Таким образом, неоднократно упоминая число 1729 в эпизодах «Футурамы», а также включив в один из эпизодов число 87 539 319, сценаристы мультсериала отдают дань уважения Рамануджану, история которого мало кому известна за пределами мира математики. Эта вдохновляющая история о гениальном человеке, который стал знаменитым благодаря преподавателю Кембриджского университета, увы, имеет трагический конец. В 1919 году Рамануджан, страдавший от различных болезней, в том числе от авитаминоза и туберкулеза, вернулся в Индию в надежде, что более теплый климат и привычная вегетарианская диета помогут ему восстановить здоровье. Однако, прожив в Индии около года, 26 апреля 1920 года он умер в возрасте тридцати двух лет.
Тем не менее идеи Рамануджана до сих пор остаются и навсегда останутся в самом сердце современной математики. Отчасти это объясняется универсальностью языка математики, а отчасти абсолютным характером математических доказательств. В отличие от идей в области искусства и гуманитарных наук, математические теоремы никогда не выходят из моды. Сам Харди сказал об этом следующее: «Архимеда будут помнить даже тогда, когда Эсхила забудут, потому что языки умирают, а математические идеи бессмертны. Возможно, “бессмертие” — глупое слово, но, по всей вероятности, математик имеет на него наибольшие шансы, что бы оно ни означало».
* * *
Присутствующие в «Футураме» ссылки на числа такси можно связать с Кеном Килером, которого считают одним из самых математически одаренных сценаристов как «Симпсонов», так и «Футурамы». По словами самого Килера, его увлеченность математикой сформировалась под влиянием отца, Мартина Килера — врача, любившего играть с числами. Каждый раз, когда они всей семьей ходили в ресторан и получали счет в конце ужина, отец искал в этом чеке простые числа и предлагал детям присоединиться к поискам. Кен Килер помнит, как когда-то он спросил отца, существует ли быстрый способ сложения квадратов целых чисел. Например, чему равна сумма квадратов первых пяти чисел, или первых десяти чисел, или первых n чисел? Доктор Килер подумал немного, а затем дал совершенно правильный ответ в виде формулы: n3/3 + n2/2 + n/6. Формулу доктора Килера можно проверить с помощью примера, скажем, когда n = 5:
Сумма квадратов первых пяти чисел: 1 + 4 + 9 + 16 + 25 = 55.
Формула доктора Килера: 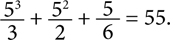
Для математика это не особо трудная задача, но не забывайте, что доктор Килер таковым не был. Кроме того, он решил ее с помощью оригинального и в высшей степени интуитивного подхода, короткое формальное объяснение которого, сформулированное Кеном Килером, представлено в .
Именно увлеченность отца математикой стала одной из причин, побудивших Кена Килера изучать прикладную математику в университете, а затем получить по этому предмету докторскую степень. Однако потом для него настали трудные времена, подталкивающие сделать выбор: Кен буквально разрывался между научной карьерой и попытками попробовать свои силы в написании комедий — еще одной области, которой он увлекался. Хотя Килер получил престижную работу в AT&T Bell Labs в Нью-Джерси, еще раньше он отправил резюме продюсерам шоу Late Night with David Letterman («Позднее шоу с Дэвидом Латтерманом»). Это был переломный момент. Когда Килеру предложили присоединиться к команде сценаристов шоу, он бросил научную работу и никогда об этом не пожалел. Килер написал сценарии для телесериалов «Крылья» (Wings) и «Критик», а затем влился в команду сценаристов мультсериала «Футурама», работая бок о бок с десятком других авторов, увлеченных математикой. Вряд ли еще где-либо в Голливуде привязанность Килера к числу 1729 получила бы столь полное понимание.
Килер внес еще один математический вклад в сериал «Футурама» — кинотеатр под названием Loews ℵ0-Plex (кинотеатр ℵ0-плекс Loews), который впервые появляется в эпизоде «Бешеный Бендер» (Raging Bender, сезон 2, эпизод 8; 2000 год). В ХХ веке компания Loews владела крупнейшей сетью многозальных кинотеатров (мультиплексов), но обозначение «ℵ0-плекс» подразумевает, что в XXXI столетии масштаб ее деятельности вырос многократно. Обозначение «ℵ0» (произносится как «алеф-ноль») — это математический символ, который представляет бесконечность. Следовательно, название кинотеатра означает, что в нем бесконечное число залов. По словам Килера, когда кинотеатр ℵ0-плекс Loews впервые появился в «Футураме», в черновом варианте сценария был комментарий, который гласил, что этот кинотеатр с бесконечным числом залов «все равно был бы недостаточно большим, для того чтобы показать фильм “Рокки” и все его сиквелы одновременно».
Хотя символ ℵ0 наверняка неизвестен большинству читателей, еще один символ для обозначения бесконечности — ∞ — мы все прекрасно знаем. Вы можете вполне резонно спросить, чем же они отличаются Символом ∞ обозначается общая концепция бесконечности, тогда как символ ℵ0 применяется только к бесконечности определенного типа!
Концепция «бесконечности определенного типа» может показаться неправдоподобной, но представленная в одной из предыдущих глав история об отеле Гильберта продемонстрировала два очевидных вывода:
- Бесконечность + 1 = бесконечность
- Бесконечность + бесконечность = бесконечность
Вывод о том, что ничего нет больше бесконечности, а также что у всех бесконечностей, так сказать, одна и та же величина, был бы слишком прост. Однако на самом деле бесконечности бывают разных размеров, что можно продемонстрировать с помощью достаточно простого доказательства.
Давайте для начала рассмотрим множество десятичных чисел в диапазоне от 0 до 1. К ним относятся как простые десятичные числа, такие как 0,5, так и числа с гораздо большим количеством десятичных знаков, например 0,736829474638…. Очевидно, что таких десятичных чисел бесконечное множество, поскольку у любого десятичного числа (скажем, 0,9) есть число еще больше (0,99), затем еще больше (0,999) и т. д. Далее мы можем сопоставить бесконечное множество десятичных чисел от 0 до 1 с бесконечным множеством натуральных чисел 1, 2, 3, …. Одно бесконечное множество больше другого или они имеют одинаковую величину?
Для того чтобы определить, какая из бесконечностей больше (в случае, если это вообще возможно), давайте представим, что произойдет, если мы попытаемся сравнить все натуральные числа со всеми десятичными числами от 0 до 1. На первом этапе следует составить список всех натуральных чисел, а затем — отдельный список всех десятичных чисел от 0 до 1. В контексте данного доказательства все натуральные числа должны располагаться по порядку, тогда как десятичные могут находиться в любом порядке. Затем эти списки необходимо разместить рядом друг с другом, по принципу один к одному.
| Натуральные числа | Десятичные числа |
| 1 | 0,70052… |
| 2 | 0,15432… |
| 3 | 0,51348… |
| 4 | 0,82845… |
| 5 | 0,15221… |
| … | … |
Гипотетически, если бы мы могли сопоставить натуральные и десятичные числа таким способом, то должно быть одинаковое количество чисел обоих типов, а значит, оба бесконечных множества имели бы одну и ту же величину. Однако установление такого взаимно однозначного соответствия невозможно.
Это становится очевидным на последнем этапе анализа бесконечности, который подразумевает создание числа, состоящего из первой цифры первого десятичного числа (в данном случае 7), второй цифры второго десятичного числа (5) и т. д. Это дает нам последовательность 7–5–3–4–1…. Затем, прибавив 1 к каждой цифре (0 → 1, 1 → 2, …, 9 → 0), мы получим новую последовательность: 8–6–4–5–2…. И наконец, ее можно использовать для создания десятичного числа — 0,86452….
Число 0,86452… интересно тем, что оно, по всей вероятности, не может входить в предположительно исчерпывающий список десятичных чисел от 0 до 1. На первый взгляд это утверждение кажется слишком смелым, но его можно проверить. Новое число не может быть первым числом в списке, поскольку мы знаем, что первые цифры не совпадают. Точно так же оно не может быть вторым числом в списке, потому что вторые цифры не совпадают, и т. д. В общем виде это число не может быть n-м числом в списке, так как n-е цифры не совпадают.
Незначительно измененные варианты этого доказательства могут продемонстрировать, что есть еще много других чисел, которые отсутствуют в исходном списке десятичных чисел. Иными словами, если мы попытаемся сопоставить два бесконечных множества, список десятичных чисел от 0 до 1 не может не быть неполным, предположительно потому, что бесконечное множество десятичных чисел больше бесконечного множества натуральных чисел.
Это доказательство представляет собой упрощенную версию диагонального метода Кантора — неопровержимого доказательства, опубликованного Георгом Кантором в 1892 году. Доказав, что некоторые бесконечные множества больше других, Кантор был уверен в том, что бесконечное множество натуральных чисел — это минимальная бесконечность, поэтому обозначил его как ℵ0 , где ℵ — первая буква древнееврейского алфавита. Кантор также считал, что множество десятичных чисел от 0 до 1 — это следующее по величине бесконечное множество, поэтому обозначил его как ℵ1 (алеф-один). Поскольку существуют бесконечные множества большего размера, их было бы логично записать как ℵ2, ℵ3, ℵ4,….
Таким образом, хотя в кинотеатре ℵ0-плекс Loews из «Футурамы» бесконечное количество залов, мы теперь знаем, что это минимальное бесконечное множество. Если бы это был кинотеатр ℵ1-плекс, в нем было бы гораздо больше залов.
В «Футураме» есть еще одна ссылка на предложенную Кантором классификацию бесконечных множеств. Математики называют множество ℵ0 счетным бесконечным множеством, потому что оно описывает масштаб бесконечности, который ассоциируется с натуральными числами, тогда как бесконечные множества большей величины обозначаются термином «несчетные бесконечные множества». Как отметил Дэвид Х. Коэн, второй термин упоминается в эпизоде «Мебиус Дик» (Möbius Dick, сезон 6, эпизод 21; 2011 год): «Мы ненадолго попадаем в эту странную четырехмерную вселенную, где встречаем множество копий Бендера, вращающихся вокруг друг за другом, а затем он возвращается в реальный мир и говорит: “Это была самая крутая несчетная бесконечная толпа парней, которую я когда-либо встречал”».

