4
Пространство-время
В предыдущих главах мы проследили исторический пути к теории относительности, и наша аргументация, по сути, была не слишком далека от первоначальных представлений Эйнштейна. Нам пришлось признать, что пространство — это не огромная сцена, на которой разыгрываются события нашей жизни. Точно так же как время не является чем-то универсальным и абсолютным. Вместо этого мы приблизились к гораздо более гибкой и субъективной картине пространства и времени. Большие часы на небе (и в каком-то смысле само небо) отправлены в изгнание. Нам может казаться, что мир — это ящик, в котором мы занимаемся своими делами, поскольку такая картина позволяет быстро и эффективно ее осмыслить. Возможность сопоставить движение объектов с воображаемой координатной сеткой представляет собой то, что можно было бы назвать чувством пространства, которое крайне необходимо для того, чтобы убежать от хищника, найти еду и выжить в опасном и сложном мире. Однако нет никаких причин, по которым эта модель, глубоко внедренная в наш мозг и подкрепленная миллионами лет естественного отбора, должна быть чем-то большим, чем просто моделью. Если некое представление о мире обеспечивает выживание, то оно обязательно станет повсеместным. Научная корректность при этом значения не имеет. Важно следующее: поскольку мы решили принять результаты экспериментов Фарадея и разъяснения Максвелла, то действовали, как подобает ученым, и отклонили удобную модель пространства и времени, которая позволила нашим далеким предкам выживать и процветать на древних равнинах Африки. Эта модель настолько глубоко внедрена в нашу психику и подкреплена миллионами лет опыта, что ее отбрасывание вполне может оказать дезориентирующее воздействие. Такое головокружительное чувство замешательства, за которым (хотелось бы надеяться) приходит прозрение и ясность, — самый притягательный момент науки. Если читатель уже чувствует первое, то к концу книги надеемся обеспечить и второе.
Это не книга по истории. Наша цель — составить как можно более понятное описание пространства и времени, а на наш взгляд, исторический путь, по которому ученые шли к теории относительности, — не лучший способ понять ее суть. Спустя столетие после открытия Эйнштейна мы знаем, что есть более глубокий и уместный способ рассуждений о пространстве и времени. Вместо того чтобы погружаться в устаревшие учебники, начнем с чистого листа. Так мы придем к пониманию того, что имел в виду Минковский, когда говорил, что «пространство и время необходимо объединить в одну сущность». Сформировав более элегантную картину, мы достигнем главной цели — выведем формулу E = mc2.
Вот наша отправная точка. Теория Эйнштейна может быть почти полностью построена на языке геометрии. Нам не нужно большое количество алгебраических формул — достаточно геометрических рисунков и концепций. В основе этого подхода лежат всего три концепции: инвариантность, причинность и расстояние. Если вы не физик, то два из этих понятий вам, скорее всего, незнакомы, а третье, возможно, известно, но, как мы вскоре увидим, здесь есть свои тонкости.
Инвариантность — это концепция, лежащая в основе современной физики. Оторвитесь от книги и посмотрите на окружающий мир. Теперь обернитесь в противоположном направлении. Ваша комната, конечно же, будет выглядеть из разных точек по-разному, но законы природы одинаковы во всех ее углах. Неважно, у северной, восточной, южной или западной стены вы находитесь — сила тяжести везде окажется одинаковой. Ваш телевизор будет продолжать работать, даже если вы повернете его экраном к стене. Ваш автомобиль будет одинаково ездить по улицам Лос-Анджелеса, Берлина и Москвы. Это все примеры инвариантности в природе. При таком толковании инвариантность кажется совершенно очевидной. Но введение требования инвариантности в научные теории оказалось на удивление плодотворным. Мы только что описали две различные формы инвариантности. Это требование неизменности законов природы при поворотах в разном направлении, которое называется поворотной инвариантностью, и требование неизменности законов природы при перемещении с места на место, называемое трансляционной инвариантностью. Эти вроде бы тривиальные требования стали необыкновенно мощным инструментом в руках Амалии Нётер, которую Альберт Эйнштейн назвал самой влиятельной женщиной в истории математики. В 1918 году Нётер опубликовала теорему, продемонстрировавшую глубокую связь между инвариантностью и законами сохранения некоторых физических величин. О законах сохранения мы еще поговорим, а пока просто упомянем о глубине полученных Нётер результатов. То, что при наблюдениях в разных направлениях законы природы остаются неизменными, подтверждает существование некой постоянной физической величины, называемой моментом импульса. (Для трансляционной инвариантности — импульс.) Почему это важно? Давайте вытащим интересный факт из нашей метафорической шляпы и объясним его.
Луна за год удаляется от Земли на четыре сантиметра. Почему? Представьте себе, что Луна находится над поверхностью вращающейся Земли в состоянии покоя. Вода в океанах непосредственно под Луной будет чуть-чуть выгибаться в сторону Луны, потому что гравитация Луны ее притягивает, а Земля под этой дугой будет вращаться со скоростью один оборот в сутки. Это и есть причина океанских приливов и отливов. Наличие трения между водой и поверхностью Земли вызывает замедление скорости ее вращения. Этот эффект невелик, но поддается измерению. Продолжительность суток на Земле постепенно увеличивается, примерно на 0,002 доли секунды за столетие. Физики описывают вращение с помощью момента импульса, поэтому можно сказать, что момент импульса Земли со временем уменьшается. Нётер утверждала, что, поскольку мир выглядит одинаково в каждом направлении (точнее говоря, законы природы инвариантны по отношению к повороту), момент импульса сохраняется, то есть общее количество вращения не должно меняться. Но что же происходит, когда момент импульса Земли уменьшается из-за приливного трения? Ответ прост: он передается Луне, которая ускоряется на своей орбите вокруг Земли, чтобы компенсировать замедление вращения Земли. А это, в свою очередь, приводит к удалению Луны от Земли. Другими словами, чтобы обеспечить сохранение общего момента импульса системы Земли и Луны, Луна вынуждена переходить на более высокую орбиту вокруг Земли, компенсируя замедление вращения последней. Это совершенно реальный и одновременно довольно фантастический факт. Луна велика и удаляется от Земли все дальше — и только потому, что законы природы одинаковы во всех направлениях. Итальянского писателя Итало Кальвино так поразил этот факт, что он написал небольшой рассказ под названием The Distance of the Moon («Отдаление Луны»), в котором представил себе далекое прошлое, когда Луна располагалась настолько близко к Земле, что наши предки забирались на нее по лестнице. Но когда с годами Луна удалилась от Земли, с наступлением ночи любителям Луны приходилось делать выбор: оставаться на Луне или возвращаться на Землю. Это удивительное (а в изложении Кальвино — удивительно романтичное) явление можно объяснить с помощью абстрактной концепции инвариантности и глубокой связи между инвариантностью и законами сохранения физических величин.
Трудно переоценить важность идеи инвариантности в современной науке. В основе физики лежит желание получить универсальную интеллектуальную структуру, законы которой бесспорны. Будучи физиками, мы стремимся раскрывать инвариантные свойства Вселенной, потому что, согласно Нётер, это приведет нас к реальным осязаемым физическим теориям. Определение инвариантных свойств не такое уж легкое занятие, поскольку глубинная простота и красота Вселенной зачастую от нас скрыты.
Ни в одной области науки это не соответствует истине в большей степени, чем в современной физике элементарных частиц, занимающейся изучением субатомного мира в поисках фундаментальных «кирпичиков» Вселенной, а также сил природы, которые соединяют их друг с другом. Мы уже встречались с одной из таких фундаментальных сил — электромагнетизмом. Его понимание привело нас к объяснению природы света, подтолкнувшему нас к путешествию по пути к теории относительности. В субатомном мире господствуют еще две фундаментальные силы природы. Сильное ядерное взаимодействие собирает нуклоны в ядра атомов, а слабое — позволяет звездам светиться и отвечает за некоторые типы радиоактивного распада. В частности, радиоуглеродный анализ определения возраста различных объектов основан на слабом ядерном взаимодействии. Четвертая сила — это гравитация: самая знакомая, но и самая слабая сила. В настоящее время лучшая теория гравитации — общая теория относительности Эйнштейна, а также, как мы увидим в последней главе, теория пространства и времени. Эти четыре силы действуют между 12 фундаментальными частицами, из которых в мире построено все, в том числе Солнце, Луна, звезды, планеты Солнечной системы и наши собственные тела. Все это представляет собой удивительное упрощение Вселенной, которая кажется на первый взгляд бесконечно сложной.
Взгляните в окно. Возможно, вы увидите город из стали, бетона и стекла или перед вами откроется сельский пейзаж с пасущимися на зеленом лугу домашними животными. Но что бы вы ни увидели, самое удивительное то, что практически каждый вид из окна — свидетельство вмешательства человека. Влияние нашей цивилизации ощущается повсюду, но все же физика XXI столетия говорит, что это не более чем математический танец горстки субатомных частиц, который более 13,7 миллиарда лет поддерживают всего лишь четыре силы. Сложность человеческого мозга и результаты эффективного синтеза сознания и опыта, которые мы видим за окном, маскируют простоту и элегантность природы. Задача ученого — обнаружить те свойства, которые, подобно розеттскому камню, позволят расшифровать язык природы и раскрыть его красоту.
Математика — тот инструмент, который помогает это сделать. Само по себе это утверждение поднимает ряд важных вопросов. В попытке найти правдоподобное объяснение подобной роли математики были написаны целые книги. Юджин Вигнер сказал об этом так: «Это чудесный дар, который мы не понимаем и которого не заслуживаем». Возможно, мы никогда не поймем истинного характера отношений между математикой и природой, но, как показывает история, математика позволяет нам организовать мышление таким образом, чтобы оно было надежным ориентиром на пути к более глубокому пониманию Вселенной.
Как мы уже неоднократно подчеркивали, придерживаясь данного подхода, физики выводят уравнения, представляющие собой не что иное, как описание взаимосвязей между различными «объектами» реального мира. Один из примеров уравнения: скорость = расстояние/время. С ним мы встречались в предыдущей главе, когда рассматривали световые часы. С помощью символов это уравнение записывается как v = x/t, где v — скорость, x — пройденное расстояние, а t — время, необходимое для прохождения расстояния x. Попросту говоря, если за час мы проезжаем 80 километров, значит, наша скорость составляет 80 километров в час. Самые интересные — уравнения, представляющие собой описание природы, приемлемые для всего без исключения. Другими словами, эти уравнения работают только с инвариантными величинами. В таком случае у всех нас, независимо от местоположения и взгляда на Вселенную, были бы одинаковые результаты измерений. В соответствии со здравым смыслом такая инвариантная величина — расстояние между двумя точками пространства, и до Эйнштейна именно так и было. Однако в предыдущей главе мы увидели, что это неверное утверждение. Помните: не всегда можно полагаться на здравый смысл. Течение времени также оказалось субъективным явлением, зависящим от скорости перемещения одних часов относительно других. Эйнштейн нарушил порядок вещей, и теперь при построении надежной картины Вселенной мы не можем полагаться даже на пространство и время. С точки зрения физика, который ищет глубинные законы природы, уравнение v = x/t не дает никакой фундаментальной пользы, поскольку не выражает соотношения между инвариантными величинами. Расшатывая пространство и время, мы поколебали сами основы физики. Что же нам теперь делать?
Один из вариантов — попытаться восстановить порядок, высказав гипотезу. Слово «гипотеза» — это замысловатое обозначение для такого простого понятия, как «догадка». Ученые постоянно выдвигают гипотезы. Не существует никаких наград за интеллектуальность теории, построенной на основе гипотезы. Опирающаяся на факты удачная догадка играет ту же роль, если только она согласуется с результатами экспериментов. Наша гипотеза радикальна: пространство и время можно объединить в одну сущность под названием «пространство-время», причем расстояния в пространстве-времени инвариантны. Это очень смелое утверждение, и его содержание постепенно станет яснее. Немного поразмышляв над ним, вы можете прийти к выводу, что оно не такое уж смелое. Если мы хотим избавиться от вековой определенности абсолютных, неизменных расстояний в пространстве и неизменного течения времени, отсчитываемого большими небесными часами, то, пожалуй, единственное, что можно сделать, — поискать некую унифицированную форму этих двух на первый взгляд не связанных друг с другом концепций. Таким образом, наша непосредственная задача — найти новую меру расстояния в пространстве-времени, которая не изменяется в зависимости от нашего движения относительно друг друга. Мы должны действовать осмотрительно, чтобы понять, как работает синтез пространства-времени. Но что именно это означает в контексте поиска расстояния в пространстве-времени?
Предположим, я проснулся в семь утра и закончил завтракать в восемь. С учетом того, что нам известно из экспериментов, верны следующие утверждения: 1) я могу измерить расстояние в пространстве от спальни до кухни, которое равно десяти метрам, но кто-то, мчащийся мимо на огромной скорости, получит другое значение этого расстояния; 2) мои часы показывают, что я потратил на завтрак час, но часы наблюдателя, мчащегося мимо на огромной скорости, покажут другое время. Наша гипотеза состоит в том, что расстояние в пространстве-времени между тем, как (и где) я встал с постели и как (и где) закончил завтракать, окажется для меня и мчащегося наблюдателя одинаковым, то есть будет представлять собой инвариантную величину. Существование подобного согласия имеет решающее значение, поскольку мы хотим создать набор законов природы на основе только этого типа объектов. Конечно, мы лишь предполагаем наличие такой инвариантной величины и пока не доказали ничего определенного. Мы даже еще не знаем, как рассчитывать расстояние в пространстве-времени. Но чтобы двигаться дальше, нам необходимо сначала объяснить, что мы подразумеваем под вторым из трех ключевых понятий — причинностью.
Причинность — еще одна на первый взгляд очевидная концепция, применение которой будет иметь глубокие последствия. Это простое требование сводится к следующему: причины и следствия настолько важны, что их порядок нельзя обратить вспять. Ваша мать — причина вашего рождения, поэтому ни одна логически последовательная картина пространства и времени не должна предусматривать возможность вашего рождения до появления на свет вашей матери. Теория Вселенной, в которой вы могли бы родиться раньше нее, была бы бессмыслицей и привела бы к возникновению противоречий. Вряд ли кто-то в состоянии спорить с требованием о сохранении принципа причинности, выраженным так просто и понятно.
Следует отметить, однако, что люди способны ежедневно игнорировать это требование. Возьмем в качестве примера пророчества. Перед такими людьми, как Нострадамус, до сих пор преклоняются за то, что они во сне или в состоянии некоего мистического транса якобы способны видеть события, которые произойдут в будущем. Другими словами, события, наступившие через столетия после смерти Нострадамуса, были известны во время его жизни, по крайней мере ему. Нострадамус умер в 1566 году, но считается, что он видел Великий пожар в Лондоне в 1666 году, появление Наполеона и Гитлера, террористические акты в США 11 сентября 2001 года, а также (наше любимое предсказание) приход антихриста в России в 1999 году. Антихрист пока еще так и не появился, но если он придет до выхода книги из печати, мы обязательно внесем поправку в текст.
Однако оставим всю эту забавную чушь в стороне, поскольку нам необходимо познакомить вас с кое-какими важными терминами. Смерть Нострадамуса была «событием», так же как и рождение Адольфа Гитлера или Великий пожар в Лондоне. Для того чтобы Нострадамус мог наблюдать, скажем, Великий пожар, который произошел после его смерти, требуется изменить порядок этих двух событий. То есть, если точнее, мы получим почти тавтологию: Нострадамус умер до Великого пожара, а значит, никак не мог его видеть. Для того чтобы Нострадамус мог его увидеть, это событие должно произойти до события «смерть Нострадамуса», а значит, порядок этих событий должен быть обратным. Здесь есть один важный нюанс: Нострадамус мог стать причиной Великого пожара. Допустим, он оставил в банке приличную сумму для того, кто темной ночью 2 сентября 1666 года подожжет Паддинг-лейн. Это позволило бы установить причинную связь между жизнью и смертью Нострадамуса и Великим пожаром в Лондоне. Как мы увидим позже, в действительности нельзя менять только порядок связанных друг с другом событий (называемых причинно связанными), то есть порядок причины и следствия, который во вселенной Эйнштейна священен.
Некоторые события достаточно удалены в пространстве и времени и не могут оказывать друг на друга никакого влияния. Интересно, что порядок таких событий можно изменить на противоположный. В теории Эйнштейна есть лазейка, позволяющая это делать при условии, что результат никак не отразится на устройстве Вселенной. Позже мы объясним, что имеется в виду под «достаточной удаленностью» событий. Пока же введем концепцию причинности как аксиому, которая будет использована нами при построении теории пространства-времени. Конечно же, верховным арбитром станет успех теории в прогнозировании результатов экспериментов. Отклоняясь от основной линии повествования, заметим, что одно предсказание Нострадамуса точно сбылось. Страдая от особенно острого приступа подагры, он сказал своему секретарю: «Утром вы не найдете меня в живых». На следующее утро мертвого Нострадамуса обнаружили лежащим на полу.
Что же нам дает концепция причинности с точки зрения понимания пространства-времени и, в частности, определения расстояния в пространстве-времени? Вскоре мы обнаружим, что требование о выполнении принципа причинности ограничивает структуру Вселенной до такой степени, что у нас просто не остается выбора в этом вопросе. Есть только один способ связать воедино пространство и время с одновременным сохранением принципа причинности. Любой другой путь приведет к нарушению этого принципа и позволит совершать такие фантастические действия, как путешествия в прошлое, чтобы предотвратить собственное рождение или, как в случае Нострадамуса, избежать того образа жизни, который спровоцировал развитие подагры.
Но вернемся к разработке концепции расстояния в пространстве-времени. Для начала ненадолго отложим разговор о времени и поразмышляем об идее расстояния в обычном трехмерном пространстве — концепции, с которой все мы хорошо знакомы. Предположим, мы пытаемся измерить расстояние между двумя городами на плоской карте Земли. Как известно каждому, кто летал на большие расстояния и наблюдал за отображением полета на карте на экране в самолете, кратчайшее расстояние между двумя точками на земной поверхности выглядит как кривая линия, которую называют большой круг. На рис. 3 показана карта Земли и линия, соответствующая кратчайшему пути от Манчестера до Нью-Йорка. На глобусе эта линия совершенно очевидна, но на плоской карте тот факт, что кратчайшее расстояние между двумя точками не прямая линия, поначалу кажется удивительным. Дело в том, что поверхность Земли не плоская, а выпуклая. Точнее говоря, Земля — сфера. Изогнутость земной поверхности — также причина того, что на некоторых плоских картах Гренландия выглядит куда больше Австралии, хотя на самом деле все наоборот. Идея ясна: прямые линии представляют кратчайшее расстояние между двумя точками только в плоском пространстве. Геометрию плоского пространства часто называют эвклидовой. Однако Эвклид не знал (как, впрочем, и все остальные до XIX столетия), что его геометрия — всего лишь частный случай семейства различных вариантов геометрии, каждый из которых математически непротиворечив, а некоторые могут использоваться для описания природы. Очень удачный пример — поверхность Земли. Она изогнута, а потому описывается с помощью неэвклидовой геометрии. В частности, в ней кратчайшее расстояние между двумя точками — не эвклидова прямая.
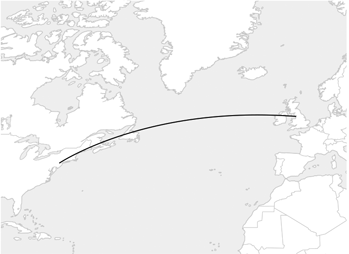
Рис. 3
Есть и другие законы эвклидовой геометрии, которым не подчиняется то, что происходит на поверхности Земли. Например, сумма внутренних углов треугольника больше не равна 180 градусам, а направленные с севера на юг линии, которые параллельны на экваторе, пересекаются на полюсах. Но если эвклидова геометрия больше не используется, то как рассчитать расстояния в искривленном пространстве, например на поверхности Земли? Один из способов — работать непосредственно с глобусом и измерять расстояния с помощью веревки. При этом выполняется корректный учет кривизны Земли. Пилот может натянуть кусок веревки между двумя городами на глобусе, измерить его длину линейкой, а затем вычислить ответ, учитывая отношение размеров глобуса и Земли. Но у нас под рукой может и не быть глобуса, или нам нужно написать компьютерную программу для управления самолетом. В любом случае требуется инструмент получше, чем веревка, так что следует вывести уравнение, показывающее, чему равно расстояние между двумя точками на земной поверхности, если известны только их широта и долгота, а также размеры и форма Земли. Такое уравнение вывести несложно, и если вы немного знакомы с математикой, то можете попробовать сделать это самостоятельно. Нам не нужно записывать здесь это уравнение — главное, что оно существует и имеет мало общего с эвклидовой геометрией плоского пространства. Тем не менее оно позволяет вычислить кратчайшее расстояние между двумя точками на сфере почти так же, как теорема Пифагора дает возможность определить кратчайшее расстояние между двумя точками (гипотенузу) на плоскости, если мы знаем расстояние между точками, измеренное вдоль координатных осей. Поскольку термин «прямая линия» относится к эвклидовой геометрии, введем новый термин для кратчайшего расстояния между двумя точками, применимый независимо от того, о каком пространстве идет речь — плоском или искривленном. Такая линия называется геодезической. К категории геодезических линий относится как большая окружность на поверхности Земли, так и прямая линия на плоскости. То же самое касается и расстояний в трехмерном пространстве. Теперь нам нужно решить, как измерять расстояния в пространстве-времени, так что давайте пойдем дальше и добавим к пространству время.
Мы уже ввели необходимые концепции, когда приводили пример с утренним пробуждением и завтраком на кухне. Расстояние в пространстве от кровати в спальне до стола на кухне составляет 10 метров. Можно также сказать (как бы странно это ни звучало), что расстояние во времени между пробуждением и окончанием завтрака равно одному часу. При обычных обстоятельствах мы рассуждаем о времени не так, поскольку не привыкли описывать его на языке геометрии. Мы скорее сказали бы следующее: «От момента, когда я проснулся, до окончания завтрака прошел один час». Точно так же мы говорим: «Встав с кровати, я должен пройти 10 метров до стула на кухне». Пространство есть пространство, время есть время, они не сомкнутся нигде. Но мы поставили перед собой задачу объединить их, потому что предполагаем, что это единственный способ обеспечить соответствие Максвеллу и Эйнштейну. Так что давайте действовать и посмотрим, куда это нас приведет. Если вы не относитесь к числу ученых, то, возможно, эта часть книги окажется для вас наиболее сложной, поскольку мы рассуждаем сугубо абстрактно. Абстрактное мышление обеспечивает силу и мощь науки, но при этом придает ей репутацию очень непростого занятия, ибо в повседневной жизни данный подход требуется крайне редко. Мы уже сталкивались с довольно сложной абстрактной концепцией электромагнитного поля, и по сравнению с ней абстракция, которая необходима для объединения пространства и времени в одно целое, гораздо проще.
Говоря о «расстоянии во времени», мы неявно вводим дополнительное измерение. Мы привыкли к слову «трехмерный», как в выражении «трехмерное пространство», поскольку оно отображает тот факт, что обычное пространство имеет три измерения: вверх-вниз, влево-вправо, вперед-назад. Добавляя в эту схему время, для того чтобы определить расстояние в пространстве-времени, мы, по сути, создаем четырехмерное пространство. Безусловно, размерность времени ведет себя не так, как размерность пространства. Мы обладаем полной свободой перемещения в пространстве и только одним способом перемещения во времени. Кроме того, наше ощущение времени никак не связано с ощущением пространства. Но это не должно быть для нас непреодолимым препятствием. Думать о времени как «еще об одном измерении» — очередной уровень абстракции, который мы должны принять. Если это звучит для вас слишком сложно, попробуйте представить себя плоским созданием, передвигающимся только вперед, назад, вправо и влево. Вы живете в плоском мире, и для вас не существует понятий «вверх» и «вниз». Если кто-то попросит вас представить третье измерение, ваш плоский ум будет неспособен это сделать. Но если у вас математический склад ума, вы можете это принять. В любом случае, даже если вы не в состоянии мысленно представить себе это дополнительное измерение, вы сможете описать его математически. Точно так же люди воспринимают четвертое измерение. По мере прочтения книги вы все больше привыкнете думать о времени как об «еще одном измерении». Когда студенты, планирующие изучать физику, впервые приходят в Манчестерский университет, мы стараемся объяснить им, что каждый может запутаться и увязнуть в каком-то вопросе. Мало кто понимает сложные концепции с первого раза, поэтому единственный способ разобраться в них — двигаться вперед небольшими шажками. То есть, как сказал бы Дуглас Адамс: «Без паники!»
Давайте продолжим, отметив один очень простой факт: в нашей жизни постоянно что-то происходит. Мы просыпаемся, умываемся, готовим завтрак, завтракаем и так далее. Все эти действия мы называем событиями в пространстве-времени. Мы можем однозначно описать событие в пространстве-времени посредством четырех чисел: трех пространственных координат, описывающих, где происходит событие, и временной координаты, описывающей, когда оно произошло. Пространственные координаты можно указать с помощью старой координатной системы — например широта, долгота и высота над уровнем моря. Скажем, координаты вашей кровати могут быть 50°28´39,75˝ северной широты, 30°20´41,57˝ восточной долготы и 172 метра над уровнем моря. Временные координаты определяются с использованием часов (поскольку время не является абсолютным, во избежание неоднозначности мы должны указать, какие именно часы используются), так что время вашего подъема, к примеру, может быть 7:00 по Гринвичу. Итак, у нас есть четыре числа, позволяющие однозначно определить любое событие в пространстве-времени. Обратите внимание, что в конкретном выборе координат нет ничего особенного. Фактически они вычисляются относительно воображаемой линии, проходящей через Гринвич в Лондоне. Это соглашение было принято в октябре 1884 года 25 странами с единственным голосом против (Сан-Доминго; Франция воздержалась). То, что выбор координат не должен иметь никакого значения, — очень важная концепция.
Давайте примем момент пробуждения в качестве первого события в пространстве-времени. Вторым событием может быть окончание завтрака. Мы уже говорили, что пространственное расстояние между этими событиями составляет 10 метров, а временное — 1 час. Для устранения неоднозначности следует добавить нечто вроде «я измерил расстояние между кроватью и столом с помощью рулетки, протянутой по прямой линии между ними» и «я измерил интервал времени с помощью своих часов, отметив их показания в моменты, когда проснулся и закончил завтракать». Не забывайте: мы уже знаем, что эти два расстояния (в пространстве и времени) не универсальны. Для того, кто летит мимо вашего дома на самолете, ваши часы будут идти медленнее, а расстояния — сокращаться. Наша цель — найти такое расстояние в пространстве-времени, с которым будут согласны все. Вот вопрос на миллион долларов: как взять 10 метров и 1 час и построить из них инвариантное расстояние в пространстве-времени? Нам нужно действовать осмотрительно и, так же как и в случае расстояний на земной поверхности, не исходить из эвклидовой геометрии.
При намерении вычислить расстояние в пространстве-времени у нас сразу же появляется насущная проблема, которую следует решить. Если расстояние в пространстве измеряется в метрах, а во времени — в секундах, то как же мы сможем их объединить? Это все равно что сложить вместе яблоки и апельсины, представляющие собой величины разного типа. Однако можно преобразовать расстояние во время и наоборот, если воспользоваться уравнением, с которым мы уже встречались ранее: v = x/t. С минимальным использованием алгебры мы можем записать время как t = x/v или расстояние как x = vt. Другими словами, расстояние и время могут быть взаимозаменяемы подобно разным денежным единицам, а «обменным курсом» будет служить скорость. Давайте введем такую калибровочную скорость и назовем ее c. Теперь мы можем измерить время в метрах, взяв любой временной интервал и умножив его на калибровочную скорость. На настоящем этапе наших рассуждений скорость c может представлять собой привычную скорость: мы еще ничего не говорили об истинном значении этого показателя. В действительности трюк со взаимозаменяемостью времени и расстояния очень распространен в астрономии, где расстояние до звезд и галактик часто измеряется в световых годах, то есть является расстоянием, которое свет проходит за один земной год. Это не кажется странным только потому, что мы привыкли, но в действительности расстояние измеряется в годах, а год — единица измерения времени. В астрономии калибрующая скорость — скорость света.
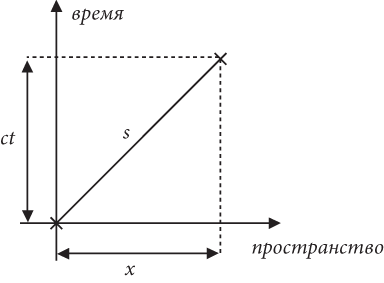
Рис. 4
Это уже прогресс: теперь у нас есть время и расстояние, измеряемые в одинаковых единицах. Например, в метрах, километрах, световых годах или еще в каких-то единицах такого рода. На рис. 4 показаны два события в пространстве-времени, обозначенные маленькими крестиками. Суть в том, что нам нужно правило, позволяющее выяснять, насколько далеко друг от друга отстоят события в пространстве-времени. Взгляните на рисунок: нам необходимо узнать длину гипотенузы по длинам двух других сторон. Для более точного описания ситуации обозначим основание треугольника как x, а высоту как ct. Это означает, что два события удалены друг от друга в пространстве и времени. Наша задача — ответить на вопрос: чему равна гипотенуза s, выраженная через x и ct? В приведенном ранее примере x = 10 метров (расстояние от кровати до стола на кухне), а t = 1 час (расстояние во времени). До сих пор значение c было произвольным, так что ct также может быть любым, но не думайте, что мы переливаем из пустого в порожнее. Мы продолжим стоять на своем.
Мы должны выбрать инструмент для измерения длины гипотенузы, или расстояния между двумя событиями в пространстве-времени. Следует ли нам выбрать эвклидово пространство (тогда мы могли бы использовать теорему Пифагора) или нечто более сложное? Возможно, наше пространство должно быть искривлено, как поверхность Земли, или иметь какую-то иную сложную форму? В действительности существует бесконечное количество способов, позволяющих вычислять расстояния. Мы поступим так, как многие физики: выдвинем предположение, в основу которого будет положен важный и полезный принцип под названием «бритва Оккама» — по имени английского мыслителя Уильяма Оккама, жившего на рубеже XIII–XIV столетий. Эту идею легко сформулировать, но очень сложно реализовать на практике. В упрощенном виде принцип звучит так: «Не нужно ничего усложнять». Оккам сформулировал его так: «Не следует множить сущности без необходимости» (что тут же приводит к вопросу, почему он не придерживался собственного правила, формулируя утверждения). Бритва Оккама — очень мощный инструмент в контексте рассуждений об устройстве Вселенной. По существу, этот принцип гласит, что первой нужно проверять самую простую гипотезу, и только если она окажется ошибочной, постепенно повышать уровень сложности, пока гипотеза не будет подтверждена экспериментальными данными. В нашем случае простейший способ построения расстояния — рассматривать как минимум пространственную часть пространства-времени как эвклидову (другими словами, считать пространство плоским). Это означает перенос старого, испытанного способа работы с расстояниями между объектами в пространстве в нашу новую схему. Что может быть проще? Остается вопрос: каким образом в эту схему добавить время? Второе упрощающее предположение — что наше пространство-время неизменно и везде одинаково. Это важные предположения. В действительности Эйнштейн ослабил их и позволил пространству-времени постоянно изменяться при наличии материи и энергии, что привело его к общей теории относительности, до сих пор являющейся самой удачной теорией гравитации. Мы познакомимся с ней в последней главе, а пока будем игнорировать все эти тонкости. Раз уж мы придерживаемся принципа Оккама и делаем два упрощающих предположения, у нас остается только два варианта вычисления расстояний в пространстве-времени. Длина гипотенузы обязана иметь вид либо s2 = (ct)2 + x2, либо s2 = (ct)2 – x2. Другого выбора нет. Хотя мы этого не доказали, гипотеза о том, что пространство-время должно быть неизменным и везде одинаковым, приводит нас только к этим двум вариантам, и мы должны выбрать либо знак плюс, либо знак минус. Безусловно, есть доказательство или нет, мы можем поступить прагматично и понаблюдать, что произойдет, когда мы испытаем каждый из вариантов.
Смена знака с математической точки зрения означает не слишком большое расширение знаменитого уравнения Пифагора. Наша задача — выяснить, следует ли придерживаться версии уравнения со знаком плюс или использовать версию со знаком минус. На первый взгляд это может показаться довольно странным. Какие вообще могут быть причины для рассмотрения уравнения Пифагора со знаком минус? Но это неверный подход. Формула для расстояния на сфере тоже не имеет ничего общего с уравнением Пифагора, так что все, что мы делаем, — просто играем с идеей о том, что пространство-время может не быть плоским в эвклидовом смысле. Действительно, поскольку версия со знаком минус — единственный вариант, кроме версии со знаком плюс (с учетом сделанных нами предположений), у нас нет логических причин отбросить ее на данном этапе. Поэтому мы должны изучить последствия. Если не подойдет ни одна из версий, значит, мы не получим работоспособную меру расстояния в пространстве-времени. И тогда будем вынуждены начать все с самого начала.
Предупреждаем: сейчас нам придется окунуться в очень элегантную, но достаточно запутанную часть рассуждений. Мы постараемся придерживаться обещания не использовать ничего сложнее теоремы Пифагора, но может так получиться, что вам понадобится прочитать этот текст не один раз. Он того стоит, потому что, внимательно следя за ним, вы сможете испытать чувство, которое биолог Эдвард Уилсон описал как ионическое очарование. Этот термин восходит к работе Фалеса Милетского, названного Аристотелем два столетия спустя основоположником естествознания в Ионии в VI веке до нашей эры. Данный поэтический термин отображает убежденность в том, что вся сложность мира объясняется посредством небольшого количества простых законов природы, поскольку природа по своей сути упорядочена и бесхитростна (вспомните эссе Вигнера). Работа ученого — отбрасывать сложности, которые нас окружают, и раскрывать лежащую в их основе простоту. Когда этот процесс приносит желаемые плоды, мы испытываем то самое ионическое очарование. Представьте себе на мгновение кружево снежинки на ладони своей руки. Эта элегантная красивая структура демонстрирует зубчатую кристаллическую симметрию. Не бывает двух одинаковых снежинок, и на первый взгляд этот хаос не может иметь однозначного объяснения. Но наука учит нас, что за очевидной сложностью снежинки скрывается лежащая в ее основе изысканная простота: каждая снежинка представляет собой конфигурацию миллиардов молекул воды H2O. Больше в снежинке ничего нет, а ее поразительно сложная структура образуется, когда молекулы H2O собираются вместе в атмосфере планеты в холодную зимнюю ночь.
Для того чтобы решить вопрос с плюсом или минусом, следует обратить внимание на принцип причинности. Давайте предположим, что уравнение Пифагора применимо и к расстояниям в пространстве-времени, то есть что s2 = (ct)2 + x 2. Теперь еще раз вернемся к нашим событиям — подъему в семь утра и завершению завтрака в восемь — и сделаем нечто такое, от чего у вас побегут мурашки по коже, когда вы вспомните, как сидели на уроках математики в школе и смотрели через окно на футбольное поле, нетронутое и зовущее в солнечный весенний день, — назовем момент пробуждения O, а завершение завтрака — A. Мы делаем это исключительно из соображений краткости, чтобы не описывать каждый раз подробно эти события.
Мы знаем, что пространственное расстояние между O и A равно x = 10 метров, а временное — t = 1 час, если x и t измеряю я. Мы еще не решили, чему равно c, но когда будем знать эту величину, то сможем вычислить и расстояние s в пространстве-времени между событиями O и A. Наша гипотеза заключается в том, что, если кто-то пролетит мимо со скоростью, близкой к скорости света, и выполнит те же измерения, расстояние s останется тем же. Иными словами, x и t для этого наблюдателя могут быть (и будут) другими, но они изменятся таким образом, что значение s останется прежним. Рискуя показаться слишком настойчивыми в подчеркивании важности этой мысли, хотим вам напомнить, что наша цель — всегда строить законы физики с использованием инвариантных объектов в пространстве-времени. Расстояние s — именно такой объект. Если это звучит слишком абстрактно, можем повторить сказанное с меньшим количеством математических терминов: правила природы должны выражать соотношения между реальными вещами, а эти вещи находятся в пространстве-времени. Вещь в пространстве-времени сродни объекту, расположенному в комнате. Пространство-время (или комната) представляет собой арену, на которой живет эта вещь. Природа реальных вещей не зависит от точки зрения и мнения наблюдателя, и в этом смысле мы говорим, что она инвариантна. Трехмерным примером чего-то, что не является инвариантной величиной, может служить мерцающая тень объекта в комнате, освещаемой пламенем из камина. Очевидно, что тень меняется в зависимости от того, как горит огонь и где находится камин, но у нас нет никаких сомнений, что за тень отвечает реальный, неизменный объект. Используя пространство-время, мы хотим вывести физику из тени и отследить соотношения между реальными объектами.
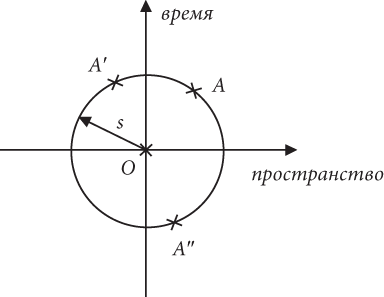
Рис. 5
Тот факт, что два разных наблюдателя могут измерить разные значения x и t, получив при этом одинаковое значение s, имеет очень важное следствие, которое довольно просто визуализировать. На рис. 5 показана окружность с центром в точке O (событие, соответствующее пробуждению в семь утра), с радиусом s. Поскольку пока мы используем формулу Пифагора для расчета расстояния, каждая точка окружности одинаково удалена от O. Это вполне очевидно: расстояние представляет собой радиус окружности. Точки вне круга находятся дальше от O, а точки внутри круга — ближе к O. Но наша гипотеза гласит, что s — это расстояние в пространстве-времени между событиями O и A. Другими словами, событие A может находиться где угодно на окружности, и при этом его расстояние в пространстве-времени от события O будет равно s. В какой же точке окружности должно располагаться событие A? Это зависит от того, кто измеряет x и t. Мне, находящемуся в доме, точно известно, что x = 10 метров и t = 1 час. На диаграмме эта точка отмечена как A. Для наблюдателя в летящей с огромной скоростью ракете расстояние в пространстве x и расстояние во времени t изменятся, но если s при этом останется неизменным, событие должно по-прежнему находиться где-то на окружности. Так что разные наблюдатели будут указывать разные положения в пространстве и времени для одного и того же события, но при этом станут подчиняться одному ограничению — все они будут находиться на указанной окружности. Обозначим два возможных положения события как A′ и A″. Что касается положения A′, то оно малоинтересно, а вот положение A″ заслуживает внимания. Здесь действительно происходит нечто весьма любопытное. A″ имеет отрицательное расстояние во времени относительно O. Другими словами, A″ происходит до O. Оно теперь находится в прошлом относительно O. Это мир, в котором вы завершаете завтрак до того, как просыпаетесь! Такое обстоятельство — очевидное нарушение принятой нами аксиомы о выполнении принципа причинности.
В качестве отступления заметим, что такие изображения, как на рис. 4 и 5, называются пространственно-временными диаграммами и очень часто помогают нам разобраться в происходящем. В действительности они довольно просты. Крестики на пространственно-временной диаграмме обозначают события. Мы можем опустить из события вертикальную линию до оси, обозначенной как «пространство», чтобы выяснить, как далеко в пространстве отстоит данное событие от события O. Аналогично горизонтальная линия от события до оси, отмеченной как «время», говорит нам о том, сколько времени прошло между данным событием и событием O. Область над осью пространства можно рассматривать как будущее для O (поскольку значение времени положительно для каждого события в этой области), а область ниже этой оси — как прошлое (так как здесь значения времени отрицательны). Проблема, с которой мы столкнулись, заключается в том, что мы построили определение расстояния s в пространстве-времени между событиями O и A, позволяющее событию A находиться как в будущем, так и в прошлом по отношению к событию O в зависимости от того, как именно движется наблюдатель. Другими словами, мы обнаружили, что требование о выполнении принципа причинности непосредственно связано с тем, как мы обозначаем расстояние в пространстве-времени, и простое определение Пифагора со знаком плюс нам не подходит.
Мы столкнулись с тем, что английский биолог Томас Хаксли описал как «великую трагедию науки — убийство красивой гипотезы уродливым фактом». Однажды Уильям Уилберфорс спросил Хаксли, которого прозвали Бульдог Дарвина за беззаветную защиту теории эволюции, по какой линии (отцовской или материнской) тот происходит от обезьяны. Хаксли ответил, что не стыдно иметь в предках обезьяну, стыдно быть человеком, использующим свой великий дар, чтобы скрывать истину. В нашем случае трагическая истина заключается в том, что мы должны отказаться от простейших гипотез, если хотим сохранить принцип причинности, и перейти к гипотезам посложнее.
Наша следующая и, по сути, единственная оставшаяся гипотеза звучит так: расстояние между точками в пространстве-времени вычисляется по формуле s2 = (ct)2 – x2. В отличие от версии со знаком плюс это мир, в котором неприменима геометрия Эвклида, как и в случае геометрии на поверхности Земли. У математиков для пространства, в котором расстояние между двумя точками описывается приведенным выше уравнением, есть свое имя: гиперболическое пространство. Физики же называют его пространством-временем Минковского. Читатель может принять это название как намек, что мы находимся на верном пути! Теперь наша главная задача — определить, не нарушается ли в пространстве-времени Минковского требование о выполнении принципа причинности.
Для того чтобы ответить на этот вопрос, нужно еще раз взглянуть на линии в пространстве-времени, точки которых находятся на одинаковом расстоянии s от точки O (то есть мы хотим рассмотреть аналоги окружностей в эвклидовом пространстве-времени). Единственное отличие — знак минус вместо знака плюс. На рис. 6 показаны наши старые знакомые — события O и A, а также линия точек, равноудаленных от точки O. Очень важно то, что эти точки больше не лежат на окружности. Сейчас они расположены на кривой, известной математикам как гипербола. С математической точки зрения все точки на этой кривой удовлетворяют нашему уравнению s2 = (ct)2 – x2. Обратите внимание, что кривая стремится приблизиться к пунктирным прямым линиям, наклоненным под углом 45 градусов к осям. Теперь ситуация в восприятии наблюдателя в космическом корабле совершенно иная, чем в версии со знаком плюс, поскольку событие A всегда находится в будущем по отношению к событию O. Событие A может перемещаться вдоль кривой, но оно никогда не окажется в прошлом по отношению к O. Другими словами, все наблюдатели согласятся, что вы проснулись до того, как позавтракали. Можно вздохнуть с облегчением: принцип причинности в пространстве-времени Минковского не нарушается.
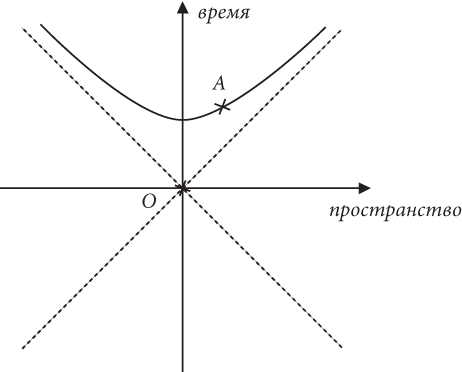
Рис. 6
Это один из важнейших моментов в книге, поэтому его стоит повторить. Если мы решили определять расстояние в пространстве-времени между двумя событиями O и A с помощью уравнения Пифагора, но со знаком минус вместо плюса, то независимо от того, кто именно рассматривает эти два события, событие A никогда не окажется в прошлом по отношению к событию O; оно просто перемещается по гиперболе. Это означает, что если событие A находится в будущем события O для одного наблюдателя, то с этим утверждением согласятся и все остальные наблюдатели. Поскольку гипербола никогда не попадает в прошлое события O, все признают то, что вы отправились завтракать после того, как проснулись.
Итак, мы только что завершили очень тонкие рассуждения. Это, конечно, не означает, что мы были правы, принимая исходную гипотезу о наличии «инвариантного» расстояния в пространстве-времени, которое будет справедливо для всех наблюдателей. Но это означает, что наша гипотеза прошла важную проверку на подчинение требованиям принципа причинности. Мы еще не закончили, потому что не просто играем с математикой. Мы физики и пытаемся построить теорию, описывающую устройство нашего мира. Конечным и решающим ее испытанием будет ее способность делать прогнозы, согласующиеся с результатами экспериментов. Но пока мы к этому не готовы, поскольку не знаем, чему равна калибровочная скорость c. Без чисел мы просто не в состоянии ничего вычислить.
Помните: для того чтобы описать понятие расстояния в пространстве-времени, нам нужно значение c, потому что измерять пространство и время необходимо в одних и тех же единицах. Пока мы не можем точно сказать, что собой представляет скорость c. Есть ли в ней что-то интересное? Ключ к ответу лежит в интригующем свойстве только что построенного пространства-времени Минковского. Эти пунктирные линии под углом 45 градусов к осям очень важны. На рис. 7 мы изобразили несколько других кривых, каждая из которых обладает свойством эквидистантности от O в пространстве-времени. Важный момент: мы можем изобразить четыре типа кривых. Одна находится полностью в будущем относительно O, другая — в прошлом, а две оставшиеся расположены слева и справа. Они внушают некоторую тревогу, поскольку пересекают горизонтальную ось так же, как и окружность, когда мы рассматривали формулу Пифагора со знаком плюс. Тогда нам пришлось отвергнуть гипотезу из-за нарушения принципа причинности. Не оказались ли мы в том же тупике в версии со знаком минус? Нет, потому что на сей раз из тупика есть выход. На рис. 7 показано событие B, расположенное в проблемной области; оно находится в прошлом по отношению к событию O. Однако эквидистантная гипербола, все точки которой размещены на одном и том же расстоянии от O в пространстве-времени, пересекает ось пространства. Это говорит о том, что могут быть как наблюдатели, для которых событие B находится по отношению к событию O в будущем, так и наблюдатели, для которых событие B находится по отношению к событию O в прошлом. Не забывайте: для всех наблюдателей расстояние между событиями в пространстве-времени одинаково, даже если по отдельности расстояние в пространстве и расстояние во времени для них различно. Хотя это выглядит как нарушение принципа причинности, к счастью, это совершенно не так.
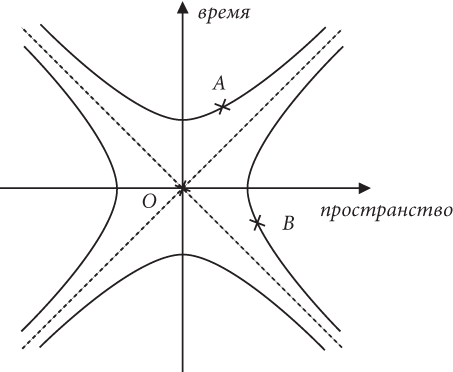
Рис. 7
Как же восстановить принцип причинности в нашей теории пространства-времени? Чтобы ответить на этот вопрос, мы должны более серьезно поразмышлять о том, что мы понимаем под причинностью. Следующая часть рассуждений будет включать космические корабли и лазеры, так что вы сможете немного отдохнуть от иссушающих мозг абстрактных понятий. Давайте вернемся еще раз к событию O — утреннему подъему. А если точнее, сопоставим это событие с моментом, когда перестает звонить будильник. Незадолго до этого с одной из планет системы Альфы Центавра, ближайшей к Земле звездной системы, находящейся на расстоянии четырех световых лет, взлетел космический корабль и направился к Земле. Должны ли все наблюдатели согласиться, что корабль стартовал до того, как я проснулся? С точки зрения принципа причинности все зависит от того, насколько быстро может распространяться информация. Если информация может путешествовать с бесконечной скоростью, то инопланетный корабль теоретически способен выпустить лазерный луч, который мгновенно достигнет Земли и уничтожит мой будильник. В результате я просплю и останусь без завтрака. Это, конечно, ужасно, но поскольку мы ставим мысленный эксперимент, давайте отвлечемся от эмоциональных последствий уничтожения моего будильника и продолжим рассуждать. Выстрел боевого лазера лишает меня завтрака, а значит, порядок этих событий не может быть изменен без нарушения принципа причинности. Это легко увидеть, так как, если бы некий наблюдатель мог прийти к выводу, что выстрел состоялся после моего пробуждения, получилось бы противоречие: я не мог бы проспать просто потому, что уже встал. Мы вынуждены сделать следующее заключение: если информация может переноситься с произвольно высокой скоростью, то порядок любых двух событий никогда не может быть изменен без нарушения закона причины и следствия. Однако в наших рассуждениях есть лазейка, которая позволяет менять порядок определенных пар событий на обратный, но только если они находятся вне 45-градусных прямых. Эти прямые действительно начинают выглядеть очень важными.
Давайте еще раз представим себе инцидент с лазером и будильником, но уже с учетом наличия некоторой предельной скорости. Другими словами, теперь мы не позволим лучу лазера бесконечно быстро перемещаться от космического корабля к нашему будильнику. Вернемся опять к рис. 7 и примем выстрел лазера за событие B. Если космический корабль выстрелит лазером (событие B) незадолго до звонка будильника (событие O), но с очень большого расстояния, то зеленые человечки никак не помешают мне проснуться, потому что лазерному лучу просто не хватит времени для того, чтобы преодолеть расстояние от космического корабля до моего будильника. Так будет в случае, если скорость луча лазера не превышает некоторого космического ограничения скорости. В этой ситуации события O и B называются причинно несвязанными.
Как показано на рис. 7, мы предполагаем, что событие B произошло незадолго до события O так, что оно находится в области правого «клина», «опасной» для принципа причинности. Различные наблюдатели могут не согласиться друг с другом в отношении того, происходит ли событие B до события O или после него, поскольку разные точки зрения соответствуют разному положению точки B на гиперболе, пересекающей пространственную ось из прошлого в будущее. Это неизбежно, но принцип причинности может быть сохранен в случае отсутствия какого-либо способа, каким событие B могло бы влиять на событие O. Иными словами, кого интересует, произошло ли событие B в прошлом или будущем события O, если это совершенно не играет никакой роли, потому что события B и O никак не влияют друг на друга? В пространстве-времени Минковского есть четыре области, отделенные друг от друга пунктирными прямыми, проведенными под углами 45 градусов к осям. Если мы хотим спасти принцип причинности, то любое событие, произошедшее в левой или правой четвертях, не должно иметь возможности послать сигнал, который бы мог достичь O.
Чтобы интерпретировать разделяющие линии, давайте еще раз посмотрим на пространственно-временную диаграмму. Горизонтальная ось представляет расстояние в пространстве, а вертикальная — во времени. Следовательно, наклоненные под углом 45 градусов прямые соответствуют событиям, для которых расстояние в пространстве от O равно расстоянию от O во времени (ct). Как быстро должен перемещаться сигнал от O, чтобы он влиял на события, лежащие в точности на 45-градусной прямой? Понятно, что если событие отстоит от O на секунду в будущем, то сигнал должен пройти расстояние c · 1 секунду. Если событие отстоит от O на две секунды в будущем, то сигнал должен пройти расстояние c · 2 секунды. Иными словами, сигнал должен распространяться со скоростью c. Чтобы сигнал дошел от события B к событию O, он должен перемещаться со скоростью, превышающей скорость c. И наоборот, для любого события, лежащего между 45-градусными прямыми в верхней и нижней четвертях, возможно сообщение между ним и событием O с помощью сигнала, скорость которого не превышает c.
Наконец-то нам удалось интерпретировать скорость c: это предельная скорость во Вселенной. Ничто не может двигаться быстрее, поскольку это могло бы использоваться для передачи информации, которая бы привела к нарушению принципа причинности. Обратите также внимание, что если все наблюдатели сойдутся во мнении о расстоянии в пространстве-времени между двумя событиями, то они должны сойтись и насчет предельной скорости c независимо от их движения в пространстве-времени. Таким образом, скорость c обладает дополнительным интересным свойством: независимо от того, как движутся два разных наблюдателя, при измерениях они всегда должны получать одно и то же значение c. Скорость c сильно начинает напоминать другую особую скорость, с которой мы уже сталкивались в этой книге, — скорость света, хотя мы еще не доказали, что это одно и то же.
Наша исходная гипотеза все еще жива. Нам удалось построить теорию пространства и времени, которая, как нам кажется, способна воспроизвести физику, с которой мы столкнулись в предыдущей главе. Безусловно, существование универсального ограничения скорости подает надежды, особенно если мы сможем интерпретировать это как скорость света. У нас также есть пространство-время, в котором и пространство, и время больше не являются абсолютными и принесены в жертву абсолютному пространству-времени. Чтобы убедиться, что мы построили возможное описание мира, давайте посмотрим, сможем ли мы получить замедление движущихся часов, с которым сталкивались в главе 3.
Представьте, что вы вернулись в пресловутый поезд, сидите в вагоне и смотрите на свои наручные часы. Вам удобно измерять расстояние относительно вашего собственного положения, а время — с помощью часов. Ваша поездка от станции до станции занимает два часа. Так как вы не покидаете своего места в вагоне, вы перемещаетесь на расстояние x = 0. Этот принцип мы установили еще в начале книги. Невозможно определить, кто именно движется, а кто находится в состоянии покоя, так что для вас, сидящего в вагоне, вполне приемлемо решение считать, что вы неподвижны. Следовательно, для вас изменяется только время. Поскольку путешествие длится два часа, в вашем восприятии вы перемещались лишь во времени. Таким образом, в пространстве-времени вы переместились на расстояние s, которое определяется как s = ct, где t = 2 часа (так как измеренное вами расстояние в пространстве x = 0). Пока все просто. Теперь рассмотрим вашу поездку с точки зрения вашего друга, находящегося не в поезде, а сидящего где-то на земле (где именно, не имеет значения, главное, что он пребывает в состоянии покоя относительно дороги, по которой со свистом несется ваш поезд). Ваш друг предпочитает измерять расстояние относительно своего положения, а время — по своим часам. Для простоты предположим, что ваш поезд едет по идеально прямой дороге. Если вы проехали два часа со скоростью v = 100 км/ч, то ваш друг отмечает, что к концу путешествия вы преодолели расстояние X = vT. Мы используем прописные буквы для расстояния и времени, измеренного вашим другом, чтобы отличать их от расстояния и времени, измеренного вами (то есть x = 0 и t = 2 часа). По словам вашего друга, вы преодолели в пространстве-времени расстояние s, определяемое по формуле s2 = (cT)2 – (vT)2.
Далее следует очень важный момент: вы оба должны указать одно и то же расстояние для вашего путешествия в пространстве-времени. Согласно вашим измерениям, вы не двигались (x = 0), а ваше путешествие заняло два часа (t = 2 часа), в то время как ваш друг утверждает, что вы проехали расстояние vT (где v = 100 км/ч), а само путешествие заняло время T. Мы обязаны приравнять полученные расстояния в пространстве-времени и выводим уравнение (ct)2 = (cT)2 – (vT)2. При преобразовании оно дает 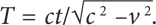 Таким образом, несмотря на то что, судя по вашим часам, путешествие длилось два часа, по часам вашего друга оно продолжалось несколько дольше, а именно — в
Таким образом, несмотря на то что, судя по вашим часам, путешествие длилось два часа, по часам вашего друга оно продолжалось несколько дольше, а именно — в 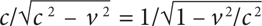 раз, что в точности совпадает с тем, что мы получили в предыдущей главе, если принять, что c — не что иное, как скорость света.
раз, что в точности совпадает с тем, что мы получили в предыдущей главе, если принять, что c — не что иное, как скорость света.
Вы начинаете чувствовать ионическое очарование? Мы вывели ту же формулу, которую получили путем рассуждений о световых часах и треугольниках в предыдущей главе. В тот момент мы говорили о световых часах потому, что выполненный Максвеллом блестящий синтез экспериментальных результатов Фарадея и других ученых привел к предположению, что скорость света должна быть одной и той же для всех наблюдателей. Этот вывод был подтвержден экспериментальными работами Майкельсона и Морли и принят в качестве постулата Эйнштейном. В этой главе мы пришли к аналогичному заключению, но без ссылок на историю или эксперимент. Нам даже не понадобилось придавать свету особую роль. Мы просто ввели пространство-время и в результате выявили, что должно существовать понятие инвариантного расстояния между событиями. Кроме того, мы потребовали неукоснительного соблюдения закона причины и следствия. После этого построили простейшую из возможных мер расстояния и получили тот же ответ, что и Эйнштейн. Это рассуждение, пожалуй, один из самых красивых примеров непостижимой эффективности математики в естественных науках. Однако истинная кульминация будет достигнута в следующей главе, а пока можем немного отдохнуть от математики и насладиться тем фактом, что мы успешно открыли новый способ размышлений о теории Эйнштейна. Пространство-время, похоже, в самом деле работает и имеет смысл, как сказал Минковский.
Как представить пространство-время? Реальное пространство-время четырехмерно, но четырехмерная природа — камень преткновения для нашего воображения: наш трехмерный мозг не в состоянии воспринимать объекты в более чем трех измерениях. Кроме того, тот факт, что одна из размерностей — время, выглядит полной бессмыслицей. Но вот картина, которая могла бы сделать все это менее загадочным. Представьте мотоцикл, едущий по холмистой местности. Вся равнина пересечена дорогами, позволяющими мотоциклу двигаться в любом направлении. Пространство-время похоже на такую холмистую равнину. Аналог движения мотоциклиста, едущего точно на север, — движение в пространстве-времени только во времени. Иными словами, такой объект неподвижен в пространстве. Конечно, утверждения наподобие «неподвижен в пространстве» субъективны, так что отождествление «направления строго на север» с «временным направлением» подразумевает определенную точку зрения, но это как раз хорошо. Нам просто следует помнить об этом. Далее, на все пересекающиеся дороги нашей равнины накладывается ограничение — они должны отклоняться от направления на север не более чем на 45 градусов. Дороги, ведущие точно на восток и запад, запрещены, так как, двигаясь по ним, нашему пространственно-временному мотоциклисту придется превысить космическое ограничение скорости в пространстве. Подумайте об этом: если бы мотоциклист мог двигаться строго на восток, он бы переместился в этом направлении на какое угодно расстояние, совершенно не затратив на это время, так как при этом абсолютно не сдвинулся бы в северном направлении. Это соответствовало бы бесконечной скорости в пространстве. Он мог бы попадать из пресловутого пункта А в пункт Б мгновенно. Поэтому дороги построены так, что мотоциклист просто не может двигаться слишком быстро в западном или восточном направлении.
Аналогии можно проводить еще дальше. Очень скоро мы покажем, что в пространстве-времени все движется с одинаковой скоростью. Это выглядит, как если бы у мотоциклиста на мотоцикле дроссельный клапан был зафиксирован в одном положении и он всегда должен был перемещаться по равнине пространства-времени с одной и той же скоростью. Говоря о скорости в пространстве-времени, следует быть осторожным, поскольку это не то же самое, что скорость движения в пространстве. Скорость в пространстве может быть какой угодно — лишь бы она не превышала космическое ограничение: например, наш мотоциклист может ехать в направлении, близком к северо-восточному, и при этом будет нестись со скоростью, сколь угодно близкой к скорости света. Напротив, выбирая дорогу, близкую к направлению строго на север, мотоциклист будет лишь немного смещаться в западном или восточном направлении, а значит, станет перемещаться в пространстве с совсем небольшой скоростью. Утверждение, что все в пространстве-времени движется с одной и той же скоростью, выглядит достаточно сильным и несколько обескураживающим. Это означает, что вы, сидящий в кресле и читающий эту книгу, проноситесь по пространственно-временной равнине с той же пространственно-временной скоростью, что и все во Вселенной. С этой точки зрения движение в пространстве представляет собой тень более обобщенного движения в пространстве-времени. В самом прямом смысле, как мы сейчас покажем, вы точно такой же мотоциклист с фиксированным дроссельным клапаном. Вы движетесь по пространству-времени с фиксированной скоростью во время чтения книги. Поскольку при этом вы спокойно сидите в кресле — ваше движение в пространстве-времени осуществляется по дороге, направленной строго на север. Если вы взглянете на свои часы, то увидите, как они измеряют пройденное вами расстояние в этом направлении. Это звучит довольно странно, так что давайте двигаться дальше очень внимательно и осмотрительно.
Почему в пространстве-времени все перемещаются с одной и той же скоростью? Вернемся опять к нашему мотоциклисту и представим, что согласно его часам прошла одна секунда. За это время он проехал определенное расстояние в пространстве-времени. Однако для всех наблюдателей оно должно быть одинаковым в силу своей универсальности, и это не может быть предметом обсуждения. То есть мы можем спросить мотоциклиста, далеко ли он заехал по пространственно-временной равнине, и ответ, который он даст, будет верным. Но мотоциклист рассматривает расстояния относительно самого себя, и с этой точки зрения он находится в пространстве на месте, а движется только во времени. Он похож на человека из главы 1, который сидит, не вставая, в кресле самолета и потому утверждает, что неподвижен. Он может двигаться по отношению к кому-либо еще — например, по отношению к человеку, стоящему на земле и провожающему самолет взглядом, — но это неважно. Так что с точки зрения мотоциклиста он вовсе не движется в пространстве, и при этом проходит одна секунда времени. Таким образом, он может использовать уравнение для пространства-времени s2 = (ct)2 – x2 с x = 0 (ведь он неподвижен в пространстве) и t = 1 секунда, чтобы выяснить, как далеко он переместился в пространстве-времени. Ответ очевиден: это расстояние в пространстве-времени равно c, умноженному на одну секунду. Итак, мотоциклист говорит нам, что перемещается в пространстве-времени на расстояние c (умноженное на одну секунду) за каждую секунду, отмеренную его часами. И это всего лишь иной способ сказать, что скорость его перемещения в пространстве-времени равна c. Если вы внимательно следили за нашими рассуждениями, то можете возразить, что прошедшая секунда измерена часами мотоциклиста и что тот, кто движется относительно мотоциклиста, измерит другой интервал времени. Это так, но в часах мотоциклиста есть нечто особенное, поскольку он неподвижен относительно самого себя (что, конечно же, тривиальное утверждение). Именно поэтому мы можем подставить x = 0 в уравнение для пространства-времени, и время, прошедшее согласно часам мотоциклиста, оказывается непосредственным способом измерять расстояния в пространстве-времени s. Это очень красивый результат: время, прошедшее на часах мотоциклиста, равно расстоянию его перемещения в пространстве-времени, деленному на c. В определенном смысле его часы представляют собой устройство для измерения расстояний в пространстве-времени, так как расстояние в пространстве-времени одинаково для всех наблюдателей. Следовательно, мотоциклист невольно использует свои часы для измерения чего-то, с чем согласятся все наблюдатели. Поэтому измеренная им пространственно-временная скорость также будет величиной, признанной всеми наблюдателями.
Таким образом, скорость перемещения в пространстве-времени — это универсальная величина, с которой согласны все наблюдатели. Этот новый образ мышления о движении в пространстве-времени может помочь нам получить другое объяснение замедления движущихся часов. При таком рассмотрении пространства-времени они используют какую-то часть фиксированной скорости в пространстве-времени на движение в пространстве и, соответственно, уменьшают часть, остающуюся для движения во времени. Иными словами, движущиеся в пространстве часы не так быстро перемещаются во времени, как покоящиеся (что представляется еще одним способом сказать об их замедлении). Напротив, часы, находящиеся в покое, движутся только во времени и не движутся в пространстве. Следовательно, они идут с максимально возможной скоростью.
Вооружившись концепцией пространства-времени, мы готовы рассматривать одну из наиболее занятных головоломок специальной теории относительности — парадокс близнецов. Ранее в книге мы показали, что теория Эйнштейна позволяет говорить о возможности путешествий в далекие места Вселенной. Например, благодаря ускорению до скоростей, близких к световым, реально добраться до галактики Андромеды за время человеческой жизни, невзирая на тот факт, что лучу света на такое путешествие требуется около 3 миллионов лет. Но здесь присутствует парадокс, о котором мы пока не рассказывали. Представьте близнецов, один из которых стал астронавтом и отправился на таком субсветовом космическом корабле в галактику Андромеды, в то время как второй остался на Земле. Близнец-астронавт движется относительно Земли с очень высокой скоростью, близкой к скорости света, следовательно, его течение времени и вся жизнь замедляются по отношению к жизни его близнеца на Земле. Но ведь мы затратили немало усилий, чтобы на страницах этой книги доказать, что не существует понятия абсолютного движения! Другими словами, на вопрос «Кто движется?» имеется единственный ответ: «Тот, кого вы выберете». Каждый из близнецов вправе решить, что в состоянии покоя находится именно он, а его брат несется по Вселенной со скоростью света. Так может решить и астронавт, находящийся в полете: это он пребывает в покое, а его близнец со скоростью света уносится вдаль вместе с Землей и Солнцем. Кто из них прав? Могут ли оба близнеца стареть медленнее по отношению друг к другу? Теория утверждает, что так и есть. Пока что в этом нет никакого парадокса, поскольку то, что каждый из них наблюдает замедление времени у своего брата, не приводит к реальным проблемам. Дело в том, что вы по привычке цепляетесь за идею универсального времени. Но время не универсально, а значит, пока что никакого противоречия. Парадокс начнется тогда, когда путешествовавший близнец вернется на Землю и встретится с оставленным там братом. Что при этом случится? Очевидно, что оба одновременно не могут быть моложе друг друга. Значит, один из них должен стать старше? Но если так, то кто именно?
Ответ можно найти в нашей трактовке пространства-времени. На рис. 8 отображены пути в пространстве-времени, пройденные близнецами и измеренные с использованием часов и линейки, находящихся в покое относительно Земли. Оставшийся на Земле близнец пребывает в состоянии покоя, а потому его путь направлен вдоль оси времени. Другими словами, вся его скорость расходуется на перемещение во времени. Со своей стороны близнец-астронавт движется со скоростью, близкой к скорости света. Возвращаясь к аналогии с мотоциклистом, это означает, что он перемещается в северо-восточном направлении, используя максимально возможную часть скорости движения в пространстве-времени для достижения скорости в пространстве, близкой к скорости света. На рис. 8 это движение в направлении, близком к 45 градусам по отношению к пространственной и временной осям. Однако в некоей точке этот близнец должен развернуться и направиться обратно к Земле. На рис. 8 показано, что он вновь движется в пространстве со скоростью, близкой к скорости света, но на сей раз — в северо-западном направлении. Очевидно, что близнецы проходят разные пути в пространстве-времени, несмотря на то что стартовали и финишировали в одной и той же точке.
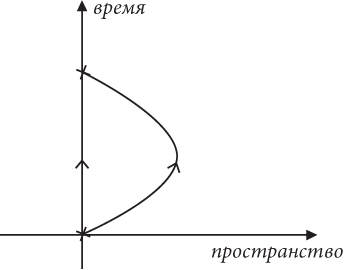
Рис. 8
Так же как и в пространстве, расстояния в пространстве-времени могут отличаться. Даже если все наблюдатели согласны с длиной некоторого пути в пространстве-времени, длины различных путей не должны быть одинаковыми. Это сродни заявлению, будто длина пути от Шамони до Курмайора зависит от того, будете ли вы двигаться в туннеле под горами или перебираться через Альпы. Понятно, что дорога через горы длиннее. В ходе обсуждения мотоциклиста, движущегося по равнине пространства-времени, мы установили, что время, измеренное с помощью его часов, дает возможность непосредственного измерения пройденного им расстояния в пространстве-времени: надо просто умножить прошедшее время на c, чтобы получить расстояние в пространстве-времени. Мы можем взглянуть на это утверждение с другой стороны и заявить, что знаем расстояние в пространстве-времени, пройденное каждым близнецом, что позволяет нам вычислить время для каждого из них. Другими словами, мы можем рассматривать каждого близнеца как путешественника в пространстве-времени, при этом пройденное ими расстояние в пространстве-времени измеряется их часами.
А теперь перейдем к ключевой идее. Взглянем еще раз на формулу для расстояния в пространстве-времени: s2 = (ct)2 – x2. Оно будет наибольшим, если следовать по пути, на котором x = 0. Все прочие пути должны быть короче, поскольку мы обязаны выполнять вычитание (всегда положительной) величины. Находящийся на Земле близнец движется вдоль оси времени с близким к нулю перемещением в пространстве, поэтому его путь должен быть самым длинным возможным путем. Фактически это просто другой способ сказать то, что мы уже знаем: близнец, оставшийся на Земле, путешествует во времени с максимально возможной скоростью, а потому стареет быстрее.
Пока что наше пояснение давалось с точки зрения земного близнеца. Чтобы полностью убедиться в том, что никакого парадокса тут нет, давайте рассмотрим ситуацию с точки зрения близнеца-астронавта. В его понимании путешествует близнец, оставшийся на Земле, в то время как он сам движется вдоль собственной временной оси. Создается впечатление, что здесь снова наблюдается парадокс: поскольку астронавт покоится относительно своего корабля, получается, что он движется с максимальной скоростью во времени, а значит, должен стареть быстрее. Однако есть один тонкий момент. Уравнение для расстояния неприменимо, если мы намерены использовать часы и линейку близнеца-астронавта. Точнее говоря, это уравнение не будет работать, когда астронавт подвергнется ускорению, разворачивающему космический корабль обратно к Земле. Почему? Аргументы, использованные нами при выведении уравнения, кажутся неопровержимыми. Но если применить ускоряющуюся систему часов и линеек для выполнения измерений (как вынужден поступить близнец-астронавт), то выдвинутое нами предположение о неизменности пространства-времени и о том, что оно одинаково в любом месте, окажется неверным. Во время ускорения близнец-астронавт будет придавлен к своему креслу, как вас вдавливает в кресло автомобиля при нажатии педали газа. В начале движения тем самым выделяется одно из направлений в пространстве: направление ускорения. В уравнении расстояния следует учесть наличие этой силы. Мы не будем излагать вам все математические детали, но итог следующий: когда корабль включает двигатели для разворота, близнец на Земле стареет быстрее астронавта, и это полностью компенсирует тот факт, что он старел медленнее во время фазы равномерного движения. Парадокса не существует.
Мы не можем устоять против соблазна привести кое-какие числовые данные. Большое космическое путешествие наиболее комфортно на корабле, который движется с ускорением, равным одному g, то есть когда путешественникам внутри корабля будет казаться, что они весят ровно столько же, сколько и на Земле. Итак, представим путешествие, в котором десять лет происходит разгон с данным ускорением, десять лет — торможение, после чего корабль разворачивается и полет повторяется в противоположном направлении — десять лет ускорения, десять лет торможения. Все путешествие занимает 40 лет. Сколько же лет при этом пройдет на Земле? Математические выкладки выходят за рамки нашей книги, так что мы просто сообщим окончательный результат: около 59 тысяч лет!
Мы тоже совершили замечательное путешествие по миру пространства-времени и надеемся, что вы следовали за нами. Теперь мы готовы перейти непосредственно к формуле E = mc2. Вооруженные пространством-временем и инвариантным расстоянием в пространстве-времени, зададим простой, но очень важный вопрос: существуют ли другие инвариантные величины, которые тоже описывают свойства реальных объектов в реальном мире? Конечно же, важны не только расстояния. Объекты имеют массу, могут быть твердыми или мягкими, горячими или холодными, жидкими или газообразными. Поскольку все объекты находятся в пространстве-времени, можно ли описать весь мир инвариантным способом? В следующей главе мы узнаем, что да и что это влечет за собой очень глубокие последствия, ибо это путь, ведущий нас непосредственно к уравнению E = mc2.

