Модели линейной регрессии применяются в самых разных деловых ситуациях для установления зависимости между переменными, которые, как подсказывает аналитику его интуиция, должны быть между собой связаны. После того как зависимость установлена, ее можно использовать для прогнозирования. Обычно регрессионный анализ используется для соотнесения продаж с ценой, рекламой и рыночными факторами; курса акций с доходами и процентными ставками; затрат на производство с объемами производства. Но, конечно, анализ можно использовать также и для ответов другие вопросы: «Как влияет температура воздуха на продажу мороженого?» Независимой переменной в этом случае является температура. Это та переменная, от которой, как предполагается, зависит все остальное. Зависимой переменной будет объем продаж. Температура на улице влияет на объем продаж, но не наоборот.

Для регрессионного анализа необходимо собрать данные, чтобы установить отношения между переменными. Когда данных много, как в случае информации по изменениям температуры и объема продаж за год, можно построить график, откладывая по оси X значения температуры, а по оси Y — объемы продаж. Цель регрессионного анализа — составить уравнение прямой, которая «наилучшим образом» отображает зависимость, то есть провести линию между нанесенными на график точками так, чтобы «значение суммы квадратов отклонений точек от линии было наименьшим». При работе методом наименьших квадратов приходится бесконечно складывать, вычитать и умножать. Для облегчения расчетов нужны калькулятор или программа построения электронных таблиц.

Перед рассмотрением примера регрессивного анализа вспомним основы алгебры. Как вы помните, прямая описывается следующей формулой:

Программа построения электронных таблиц рассчитывает линейное уравнение (Y = mX + b), описывающее связь между независимой и зависимой переменными. Программа определяет, можно ли использовать прямую, «наилучшим образом» отображающую эту связь, в качестве точного инструмента прогнозирования.

Владелец сети из двадцати магазинов по продаже мороженого Ben & Jerry’s заметил, что объемы продаж растут и снижаются вместе с ростом и понижением температуры воздуха. Решив определить точную математическую зависимость между объемом продаж и сезонными температурами, он собрал данные по ежемесячным объемам продаж за предыдущие пять лет, а в Национальной метеорологической службе получил данные по среднемесячным температурам. В результате получилась следующая таблица (5.3):

Используя функцию «Regression» программы построения электронных таблиц, владелец получил следующий результат (табл. 5.4):

Поразительно: этот набор данных позволяет составить уравнение прямой, выражающей зависимость между температурой и объемами продаж в магазинах Ben & Jerry’s. Сначала объясним данные, на основе которых составляется линейное уравнение.

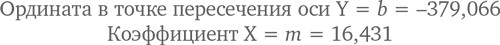
Подставляя эти значения в стандартное линейное уравнение, которое мы припомнили из курса алгебры, получаем: Y = 16,431X – 379,066. Наносим точки на график и проводим линию регрессии, описанную этим уравнением. В результате получаем (рис. 5.24):

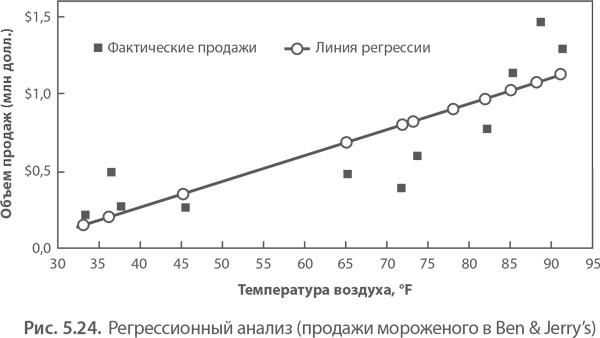
На графике видно, что линия регрессии проходит посредине между точками данных. Введя значение температуры X в уравнение, можно определить прогнозируемый объем продаж мороженого. В случае с Ben & Jerry’s при температуре 60 °F (15 °С) ожидаемый объем продаж за месяц должен составить $606 794.

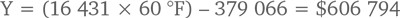
Однако насколько точно данное уравнение позволяет прогнозировать продажи мороженого? Чтобы ответить, нужно присмотреться к другому числу в таблице.

Значение R-квадрат показывает, «какой процент разброса данных объясняется данным регрессионным уравнением». В нашем случае это 70,4% разброса данных по объему продаж — очень высокий показатель. В более масштабном экономическом анализе очень высоким будет считаться показатель 30%, так как на состояние экономики влияют тысячи переменных. Можно предположить, что в бизнесе, связанном с мороженым, на колебания объема продаж, помимо температуры, влияют также реклама, скидки, часы работы магазина.

Однако будьте бдительны! Не придавайте излишнего значения результатам регрессионного анализа! Они говорят нам только то, что объем продаж определенным образом изменяется при изменении температуры. Из этого анализа не следует, что «температура всегда влияет на объем продаж». Но если вы рационально и обоснованно выбрали независимую переменную и она хорошо предсказывает поведение зависимой переменной, значит, метод годится.

Регрессионный анализ выявляет не только позитивную, как в случае с температурой воздуха и объемом продаж мороженого, но и негативную корреляцию, например, процентных ставок и объема продаж жилья. Если процентные ставки слишком высоки, объем продаж низок и коэффициент X имеет отрицательное значение. С точки зрения прогнозирования подобные негативные зависимости так же полезны, как позитивные.

«Среднеквадратичная погрешность оценки Y» и «среднеквадратичная погрешность коэффициента X» — синонимы стандартного отклонения ошибки коэффициента Y и коэффициента X графика регрессии. В примере с компанией Ben & Jerry’s среднеквадратичная погрешность оценки Y (объем продаж) составляет $243 334 в 68% случаев (табл. 5.4), а коэффициента X (температура) — 3367 (табл. 5.5). Можно провести ряд анализов, устанавливая диапазон этих данных и надежности с учетом среднеквадратичного отклонения, и проверить надежность полученного уравнения регрессии.

T-статистика может подсказать, пригодно ли для прогнозирования уравнение регрессии, рассчитанное компьютерной программой: T-статистика проверяет, оказывает ли переменная X статистически значимое влияние на Y, как, например, температура воздуха — на объем продаж. Для определения данного критерия следует разделить коэффициент X на его среднеквадратичную погрешность. Если T-статистика окажется больше 2 или меньше –2, переменная X оказывает статистически значимое влияние на Y. В нашем примере критерий имеет очень высокое значение: 16431/3 367 = 4,88 (см. табл. 5.5). Поэтому аналитик делает вывод, что по температуре можно с высокой достоверностью прогнозировать объем продаж.

Модель прогнозирования подходит при высоких значениях и R, и T-статистики. Можно разработать модель более чем с одной переменной X. Мы будем иметь дело с многомерной регрессией. С ростом числа переменных увеличивается значение R. Однако прибавление числа переменных X при низком значении T-статистики приводит к неточной модели. Необходимо работать над моделью, добавляя и исключая независимые переменные, чтобы получить высокие значения R и T-статистики.

Один из приемов регрессионного анализа — метод фиктивных переменных для представления условий, не определяемых в серии расчетов. В качестве таких переменных берутся значения 0 и 1. Например, магазин Toys “R” Us, имеющий запас модной игрушки — условие, которое нельзя выразить численным значением, — резко увеличивает объем продаж. В совокупности данных наличие и отсутствие запаса можно обозначить ранговыми переменными 1 и 0 соответственно.

Используя гипотетическую совокупность данных по магазину Toys “R” Us, можно понять, как работают эти переменные (табл. 5.6).

Выводы регрессивного анализа устанавливают отношения между модной игрушкой и уровнем продаж:

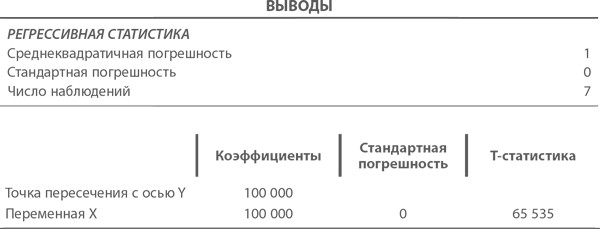
Это идеальная модель, поскольку разброс на 100% объясняется среднеквадратичной погрешностью, и T-статистика работает прекрасно. T-статистика огромна. Уровень продаж составляет $100 000, когда модная игрушка отсутствует в ассортименте, и увеличивается на $100 000, когда она появляется. Уравнение регрессии по данным электронной таблицы имеет вид:

Объем продаж = 100 000Х + $100 000

Если вожделенная игрушка имеется в магазине, X = 1 и объем продаж подскакивает до $200 000, если не имеется, Х = 0 и продажи возвращаются на уровень $100 000. Фиктивные переменные весьма полезны и могут использоваться для установления соответствий между немасштабными данными, такими как наличие запасов или количества выходных, с поддающимися измерению данными, такими как температура, процентная ставка и дефекты продукции. В результате получаются удобные регрессивные модели.