Теория вероятности — красивое название статистики, предмета, которого побаиваются даже наиболее талантливые слушатели бизнес-школ. По существу, теория вероятности — более точный термин, поскольку он объясняет, как статистика используется для решения задач. При определенной вероятности обнаружения нефти как следует поступить Сэму? Сколько из 800 состоящих в браке слушателей лучших рейтинговых школ на первом году программы MBA позабудут о своих супругах? Все это теория вероятности. Почти все деловые люди избегают статистики, тут-то МВА и предоставляется возможность блеснуть. Я прослушал курс статистики еще в студенчестве и практически ничему не научился, так как нам преподавали теорию, а не решение проблем. Программы для МВА сосредоточены на практическом применении статистики, а теорию оставляют математикам. Если вы незнакомы со статистикой, ни в коем случае не пропускайте этот раздел. Нескольких страниц не хватит, чтобы сделать вас знатоком статистики, но если вы наберетесь терпения и прочтете эту главу, то будете разбираться в этом сложном вопросе достаточно, чтобы вовремя попросить о помощи. В том-то и суть подготовки MBA — дать слушателям практические знания по различным предметам. Преподаватели не надеются за два года превратить учеников в экспертов, но требуют, чтобы выпускники понимали, когда им требуется помощь эксперта для решения конкретной проблемы.

В ситуациях с множественными возможными исходами подсчитывается их распределение. Каждому исходу приписывается определенная вероятность. С помощью тщательного анализа и интуиции вычисляются все возможные исходы того или иного события. Сумма вероятностей всех исходов равна 100%, как и на любом разветвлении дерева решений. График распределения исходов называется вероятностной мерой или плотностью вероятности. Когда вероятных исходов много, кривая получается плавной и в этом случае называется функцией плотности вероятности. Если возможных исходов всего несколько, кривая неровная, и в этом случае она называется вероятностной мерой.

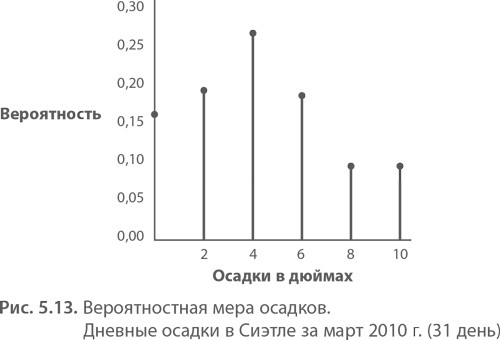
Пример с дождями. Дождь в Сиэтле — событие, характеризуемое определенным распределением вероятностей. В соответствии с гипотетическими данными выпадение дождей в Сиэтле можно представить в форме таблицы и графиков распределения вероятностей (табл. 5.1).

Подбрасывание монеты имеет два вероятных исхода — монета падает орлом или решкой кверху. Поэтому распределение исходов двух подбрасываний монеты дает несколько разных результатов с точки зрения того, кто поставил на орла.

Двойная удача — орел/орел.

Одна удача / одна неудача — орел/решка.

Двойная неудача — решка/решка.

Подбрасывание монеты описывается самым простым видом распределения вероятностей — биномиальным. При биномиальном распределении существует всего два одинаково вероятных исхода — удача и неудача.

«Тайную теорию» биномиального распределения можно применить к такому практическому делу, как анализ рынка акций. Удачей на рынке можно считать прибыль по итогам месяца, а неудачей — убыток или нулевую прибыль. В исследовании динамики цен на акции компании AT&T за период с 1957 по 1977 г. был проанализирован каждый месяц и установлена пропорция удачных месяцев: в 56,7% случаев за двадцатилетний период успех был обеспечен.

Исследованные месяцы были объединены в группы по три (кварталы). Исследователи выявили частоту событий с благоприятным исходом (рис. 5.14):

Математик, подбрасывавший монету, составил таблицы для решения всех задач по биномиальному распределению. В случае с компанией AT&T для пользования такой таблицей необходимо иметь следующую информацию:

r = число благоприятных исходов = от 0 до 3;

n = число попыток = 3 (3 месяца в квартале);

р = вероятность благоприятного исхода = 56,7%.

На основании этой информации таблица биномиального распределения предсказывает ожидаемые исходы (рис. 5.15):

Как ни странно, биномиальное распределение довольно хорошо коррелирует с фактическими результатами по AT&T. При данной вероятности благоприятного исхода (p) вероятность получения прибыли по итогам месяца за конкретный квартал можно узнать из таблицы. Поэтому инвестиционные менеджеры, директора по продажам и аналитики могут делать из биномиального распределения практические выводы.

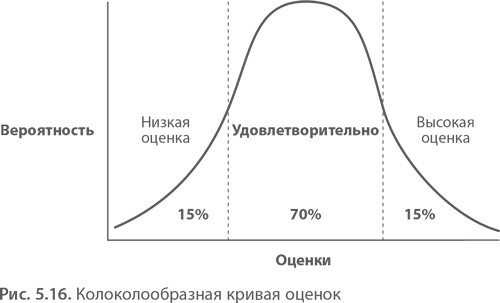
Нормальное распределение встречается чаще всего, а его графическое представление обычно называют колоколообразной кривой. В Гарварде при выставлении оценок используют колоколообразную кривую. Кривая показывает, что 15% слушателей получают низкую оценку (проходной балл). В Дарденской бизнес-школе преподаватели ставят неудовлетворительную оценку, основываясь на собственном суждении. Результат: в двух кампусах сложилась принципиально разная конкурентная среда.

Когда вероятностная мера выводится на основании множества проб, точки кривой сближаются, и она принимает колоколообразные очертания. Такую кривую мы называем функцией плотности вероятности. Именно так выглядели графики осадков в Сиэтле. Горб посреди кривой объясняется центральной предельной теоремой. Она гласит, что «распределение средних арифметических для повторяющихся независимых выборок принимает форму колоколообразного нормального распределения». Почему? Просто потому, что при большом числе независимых выборок итог стремится к центральному среднему арифметическому.

Концепция «средних по выборкам» довольно расплывчата. На практике речь идет о достаточно больших группах данных. Почему? Потому что нормальное распределение легко использовать, и оно всегда оказывается близко к реальности. Курс акций — это отражение многочисленных конъюнктурных колебаний на рынке, результатом которых будет благоприятный или неблагоприятный исход. Этот результат можно рассматривать в качестве «среднего арифметического» конъюнктурных колебаний. Едва ли не все происходящее можно рационализировать через среднее арифметическое, и этим объясняется полезность нормальных распределений.

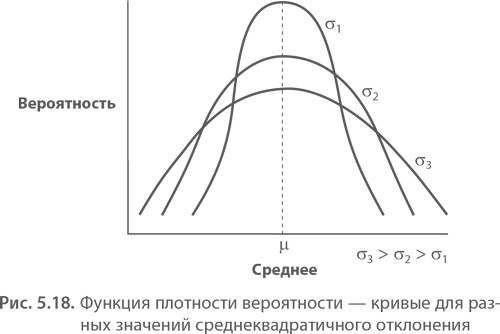
Параметры нормальной кривой. Колоколообразная кривая характеризуется двумя параметрами: средним и стандартным (среднеквадратичным) отклонением (СКО). Среднее (μ) является центром кривой. Обычно его называют средним арифметическим. Оно вычисляется делением суммы значений на их количество. Среднеквадратичное отклонение (σ) определяет ширину кривой. СКО можно также описать как критерий «отклонения от среднего». Две эти характеристики играют ключевую роль в большей части концепций теории вероятности.

Другие критерии средней величины для совокупности данных — медиана, величина, стоящая в середине упорядоченного по возрастанию списка данных, и мода — величина, чаще всего встречающаяся в выборке.

Как и в случае биномиального распределения, сумма всех исходов, представленная площадью под кривой, равна 100%. Особенность нормальной кривой заключается в том, что для любого среднеквадратичного отклонения от среднего или центра вероятность события одинакова, независимо от формы кривой.

Пример нормального распределения из розничной торговли. Эл Банди, владелец обувного магазина, хочет быть уверен, что на складе имеются запасы обуви любого размера. Он купил в Академии ног данные по частоте женских ног и получил результаты проведенного Академией опроса.

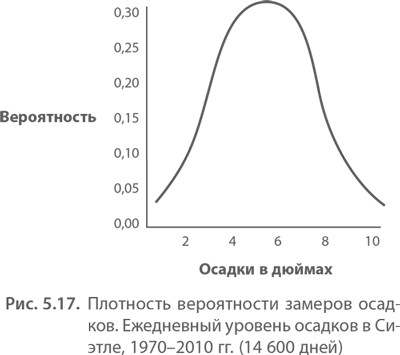
На миллиметровке Банди расположил эти данные и получил нормальное распределение. Он также ввел данные в свой калькулятор и нажал кнопку «стандартное отклонение». Ответ был «2». Эл также проверил среднее арифметическое для всей совокупности ответов по размерам и получил ответ «7». Посмотрев на кривую, он увидел внушающее доверие нормальное распределение (рис. 5.17).

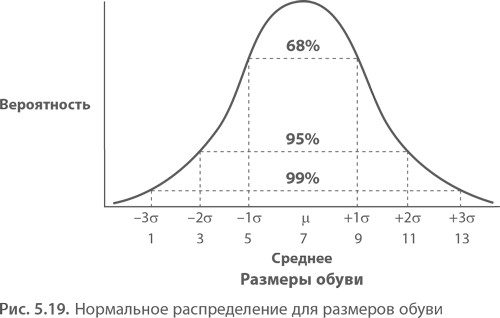
Как только Эл распознал кривую, он смог применить законы нормального распределения. Площадь участков под нормальной кривой всегда описывается формулой:

1 СКО = 0,3413

2 СКО = 0,4772

3 СКО = 0,49865

4 СКО = 0,4999683

Если мистер Банди, учтя эти данные, запасет размеры с 5-го по 9-й, он сможет удовлетворить потребности 68,26% (0,3413 × 2) покупательниц. Расширив ассортимент склада с 3-го по 11-й размеры, он сможет обуть 95,44% женщин. Если же Эл будет иметь на складе размеры с 1-го по 13-й, 99,73% клиентов уйдут от него с покупкой. Для тех, у кого размер меньше 1-го или больше 13-го, он может сделать специальный заказ.

Естественно, таблицы нормальных распределений составлены для определения вероятности любой конкретной точки на кривой (с учетом нецелочисленных СКО). Для пользования таблицами необходимо рассчитать значение Z.

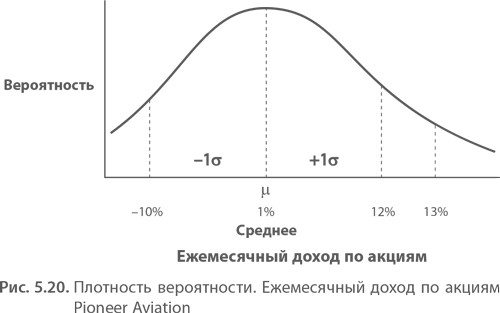
Давайте применим новые правила теории вероятности к финансовой деятельности. Ежемесячная прибыль на колеблющиеся акции компании Pioneer Aviation представлена в виде кривой нормального распределения. Сводные данные по прибыли в ретроспективе показывают, что среднее равно 1%, а СКО (разброс) — 11%. Джеральд Расмуссен хочет узнать, какова вероятность получить в следующем месяце прибыль менее 13%.

Используя формулу расчета Z, мы можем составить формулу:

Таблица нормального распределения, которую я привожу в Приложении, говорит нам, что 1,09 СКО равно 0,3621. Площадь участка под всей левой половиной кривой равна 0,5000, так как она представляет половину распределения. Это верно в любой ситуации. Вероятность попадания в точку, находящуюся выше или ниже центра или среднего нормального распределения, равна 50%. Исходя из приведенных данных, определяем вероятность того, что прибыль на акции окажется ниже 13%: 0,3621 + 0,5000 = 0,8621, и, с другой стороны, — что она окажется выше 13%: 1 – 0,8621 = 0,1379. Это реальный ответ на реальную деловую задачу с использованием инструмента статистики.

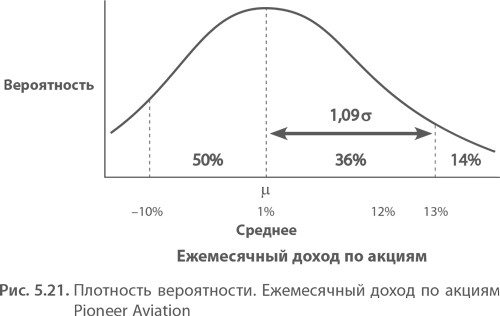
Статистика не трудна, если не напирать чересчур на теорию. Существуют и другие распределения, но их редко используют в бизнесе. Распределение Пуассона сходно с нормальным распределением, но имеет удлиненный хвост в правой части графика. Однако в большинстве случаев распределение считается нормальным, так как это позволяет использовать правила стандартного отклонения.

Кумулятивная функция распределения дает интегральную картину распределения вероятности. Она рассматривает функцию вероятностной меры типа колоколообразной кривой и задает вопрос: «Какова вероятность того, что результат окажется меньше или равен такому-то?» Нормальная кривая показывает вероятность конкретного значения, a кумулятивная функция — вероятность данного спектра значений. Кумулятивная функция позволяет объединить понятие о неопределенности (теорию вероятности) с нашим инструментом для принятия решений (дерево решений). Она охватывает весь спектр возможных исходов при анализе переменных с множественными значениями.

Вернемся к примеру с нефтяной скважиной и посмотрим распределение значений возможной стоимости нефти (табл. 5.2):

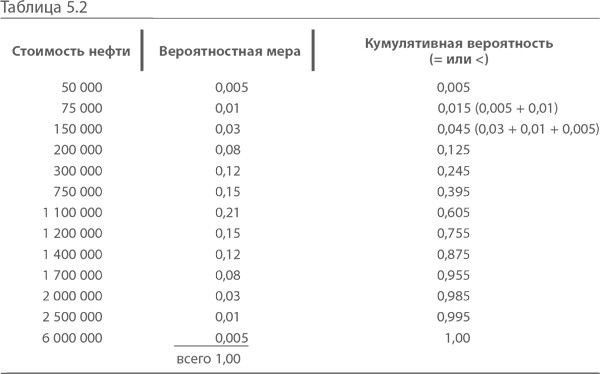
При построении дерева решений мы исходили из возможного выигрыша в миллион. Такова была ожидаемая стоимость нефти — я выбрал эту сумму ради удобства. При распределении мы получаем широкий спектр значений. Как видно из таблицы, с вероятностью 0,005 прибыль может оказаться равной $6 млн и $50 000. Если все эти суммы умножить на соответствующие вероятности, указанные во втором столбце, а затем сложить произведения, получится тот самый $1 млн, ожидаемая стоимость.

Построив функцию кумулятивного распределения, человек, принимающий решение, устанавливает среднее, то есть ожидаемую стоимость, и с этого может начать анализ. Построение кумулятивного распределения позволяет объединить оценки вероятности верхней границы, середины и нижней границы спектра исходов и установить ожидаемую стоимость, что позволит принять решение.

В графической форме кумулятивное распределение исходов в диапазоне напоминает большую букву «S». На такой кривой сразу видны все возможные исходы, а не только разрозненные статичные точки. Как показано на следующем графике, Сэм Хьюстон считает, что все возможные в данном случае исходы попадают в непрерывный диапазон значений от 0 до $6 000 000.

Диапазон вероятностей от 0 до 1,0 кумулятивного распределения разбивается на части — квантили — методом медиан интервального ряда. В таблице именно так разделена ожидаемая стоимость. Например, чтобы разделить диапазон вероятности ожидаемой стоимости на пять частей, нужно взять квантили 0,1; 0,3; 0,5; 0,7 и 0,9. Эти квантили будут представлять собой среднее арифметическое в диапазонах значений 0–0,2; 0,2–0,4; 0,4–0,6; 0,6–0,8 и 0,8–1,0 соответственно.

Квантиль 0,5 равнозначен медиане, поскольку с каждой его стороны находится ровно половина возможных значений. Медиана не обязательно совпадает со средним, то есть центром нормального распределения. Медиана — это просто центр диапазона значений. Среднее — это сумма произведений всех вероятностей на соответствующие значения: именно так мы получили ожидаемую стоимость обнаружения нефти $1 млн.

Чтобы объединить концепцию кумулятивного распределения с деревом решения и принимать существенные управленческие решения, нужно представить себе все вероятные значения прибыли от нефтяной скважины. Диапазон значений можно изобразить в виде веера событий. Кому-то может не хватить терпения для представления бесконечных возможностей в виде ветвей дерева, и тут выручит кумулятивная вероятность.

Рисуем кумулятивное распределение. Чтобы представить кумулятивное распределение в графической форме, как показано ниже, следует опираться на собственное суждение и данные исследований. Нужно задать себе ряд вопросов:

При каком значении в 50% случаев результат оказывается выше или ниже заданного значения (медиана)?

Каким будет значение нижнего конца спектра (квантиль 0,10)?

Каким будет значение верхнего конца спектра (квантиль 0,90)?

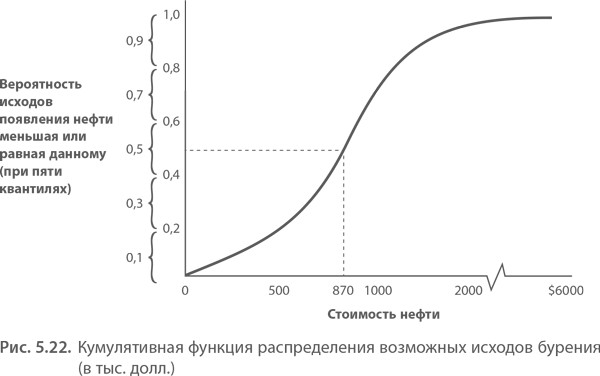
Ответив на эти вопросы, вы сможете представить кумулятивную стоимость возможных исходов. Ограничившись пятью исходами или пятью квантилями кумулятивного распределения, вы можете изобразить веер событий и их вероятностей на дереве решений в виде пяти ветвей.

Ожидаемый денежный эквивалент будет таким же, как при первом рассмотрении, но только потому, что с самого начала для удобства была задана правильная величина ожидаемой стоимости.

Сокращенный вариант такого анализа называют методом Тьюки–Пирсона. Вместо пяти квантилей используется всего три — 0,05; 0,5 и 0,95. Соответствующие этим квантилям вероятности — 0,185; 0,63 и 0,185.

Применительно к крупным задачам дерево решений строится с помощью компьютерных симулякров Монте-Карло, самый популярный из них — Oracle. Дерево и параметры «веера событий» кумулятивного распределения включены в компьютерную модель. Программа прогоняет множество сценариев событий, чтобы дать вам представление, чем может обернуться дело. Некоторые из компаний Fortune 500 используют этот метод.

Кумулятивное распределение и анализ методом квантилей можно применять к ситуациям, в которых ожидаемая стоимость ветви дерева решений неопределенна. Однако важнее всего суждение аналитика. Дерево — это всего лишь инструмент, который МВА обязан использовать в сочетании со своими знаниями и интуицией.