Экспоненциальное сглаживание Холта с корректировкой тренда

Книга: Много цифр. Анализ больших данных при помощи Excel

Дальше: Мультипликативное экспоненциальное сглаживание Холта – Винтерса

Экспоненциальное сглаживание Холта с корректировкой тренда распространяет простое экспоненциальное сглаживание на создание прогноза из данных, имеющих линейный тренд. Часто оно называется двойным экспоненциальным сглаживанием, потому что в отличие от простого ЭС, имеющего один параметр сглаживания – альфа, и один компонент, не являющийся отклонением, двойное экспоненциальное сглаживание имеет их два.

Если у временной последовательности линейный тренд, то его можно записать так:

спрос за время t = уровень+ t × тренд + случайное отклонение уровня в момент времени t

Самое последнее приближение уровня и тренда (умноженные на количество периодов) служит прогнозом на грядущие периоды времени. Если сейчас месяц 36, то каким будет хорошее приближение спроса на период 38? Приближение последнего периода времени плюс два месяца тренда. Не настолько просто, как ПЭС, но близко.

Теперь, как и в простом экспоненциальном сглаживании, вам нужно получить несколько исходных приближений значений уровня и тренда, которые мы обозначим уровень₀ и тренд₀. Один из простейших способов их найти – это просто изобразить на графике первую половину ваших данных о спросе и определить линию тренда (как мы делали в главе 6 в примере с аллергией на кошек). Уклон этой линии – тренд₀, а у-начальный отрезок (свободный член) – уровень₀.

Экспоненциальное сглаживание Холта с корректировкой тренда имеет два новых уравнения, одно – для уровня по мере его продвижения во времени, а другое – собственно тренд. Уравнение уровня также содержит сглаживающий параметр под названием альфа, а в уравнении тренда используется параметр, часто называемый гамма. Они абсолютно одинаковые – просто значения от 0 до 1, регулирующие вмешательство погрешности одношагового прогноза в дальнейшие расчеты приближений.

Вот как выглядит новое уравнение уровня:

уровень₁ = уровень₀ + тренд₀ + альфа × (спрос₁ – (уровень₀ + тренд₀))

Обратите внимание, что уровень₀ + тренд₀ – это просто одношаговый прогноз от исходных значений к месяцу 1, поэтому (спрос₁ – (уровень₀ + тренд₀)) – это одношаговое отклонение. Это уравнение очень похоже на уравнение уровня из ПЭС, за исключением того, что считается значение тренда за один период, когда бы вы ни рассчитывали следующий шаг. Таким образом, основное уравнение приближения уровня будет следующим:

уровень текущий период= уровень предыдущий период + тренд предыдущий период + альфа × (спрос текущий период – (уровень предыдущий период + трендпредыдущий период))

Для этой новой техники сглаживания нам понадобится новое уравнение обновления тренда. Для первого шага оно будет таким:

тренд₁= тренд₀ + гамма × альфа × (спрос₁ – (уровень₀ + тренд₀))

То есть уравнение тренда очень похоже на уравнение обновления уровня. Берется предыдущее приближение тренда и изменяется на гамму, умноженную на размер отклонения, заложенного в соответствующее обновление уровня (которое имеет интуитивный смысл, потому что только некоторые из отклонений, используемых для изменения уровня, можно отнести к небольшим или скачкообразным приближениям тренда).

Таким образом основное уравнение приближения тренда такое:

трендтекущий период = трендпредыдущий период + гамма × альфа × (спрос текущий период – (уровень предыдущий период + трендпредыдущий период))

Настройка холтовского сглаживания с коррекцией тренда в электронной таблице

Для начала создайте новый лист под названием Holt’s Trend-Corrected. Затем, как и в случае с таблицей простого экспоненциального сглаживания, скопируйте в строку 4 временной ряд данных и вставьте пустую строку 5 для исходных приближений.

Столбец С снова будет содержать приближения уровня, а столбец D – приближения тренда. Наверху в этих столбцах находятся значения альфы и гаммы. Вы оптимизируете их «Поиском решения» за секунду, но сейчас пусть они будут около 0,5. Так получается таблица, изображенная на рис. 8-12.

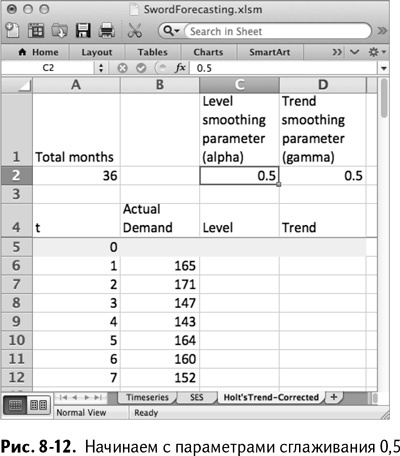
А для исходных значений уровня и тренда в С5 и D5 мы построим график за первые 18 месяцев и добавим в него линию тренда с уравнением (если вы не знаете, как добавить на график линию тренда, обратитесь к главе 6). Так мы получаем исходное значение тренда 0,8369 и исходный уровень (свободный член линии тренда), равный 155,88.

Добавив данные в D5 и С5 соответственно, получаем лист, изображенный на рис. 8-13.

Теперь добавьте в столбцы E и F столбцы прогноза и погрешности прогноза на один шаг вперед. Если посмотреть на строку 6, одношаговый прогноз получается примерно равным предыдущему уровню, к которому прибавлен тренд за один месяц с помощью предыдущего приближения – это С5+D5. Погрешность прогноза вычисляется так же, как и в случае простого экспоненциального сглаживания: F6 – это просто текущий спрос, из которого вычтен одношаговый прогноз – В6–Е6.

Теперь вы можете обновить значение уровня в ячейке С6 – оно будет равно предыдущему значению, к которому прибавлен предыдущий тренд и альфа, умноженная на погрешность:

=C5+D5+C$2*F6

Тренд в D6 обновляется точно так же, только нужно еще прибавить гамму, умноженную на альфу, умноженную на погрешность:

=D5+D$2*C$2*F6

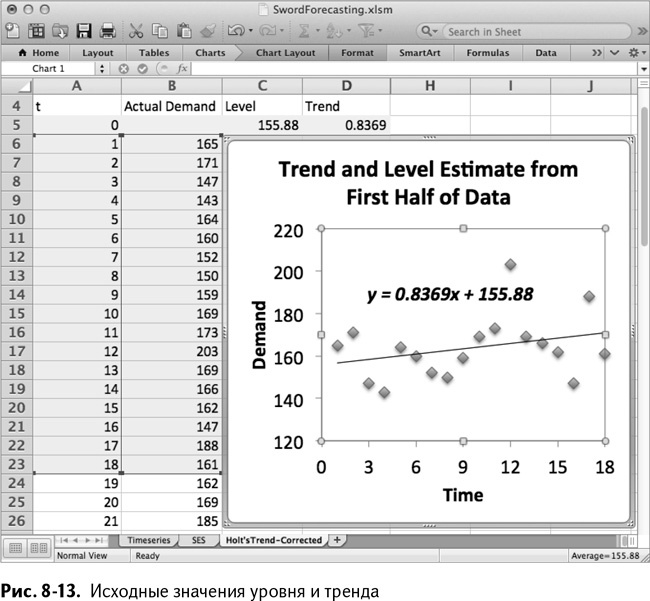
Обратите внимание на следующую деталь: необходимо использовать абсолютные ссылки на альфу и гамму, чтобы была возможность растянуть формулу на целые столбцы. Сделайте это прямо сейчас – растяните С6:F6 вниз до месяца 36. Операция показана на рис. 8-14.

Прогнозируем будущее

Чтобы прогнозировать дальше, чем на 36 месяцев, добавьте итоговый уровень (который для альфы и гаммы, равных 0,5, будет равняться 281) к количеству месяцев после 36-го, на которые вы хотите рассчитать прогноз, умноженному на итоговое приближение тренда. Вы можете подсчитать количество месяцев от 36 до нужного вам, вычтя один месяц в столбце А из другого.

К примеру, для прогноза месяца 37 в ячейке В42 вы будете пользоваться такой формулой:

=C$41+(A42-A$41)*D$41

С помощью абсолютных ссылок на месяц 36, итоговый тренд и итоговый уровень, прогноз можно растянуть вниз до месяца 48, что показано на рис. 8-15.

Как и в таблице простого экспоненциального сглаживания, здесь можно построить график исторического спроса и прогноза как двух серий данных на одной простой координатной плоскости, как показано на рис. 8-16.

При альфе и гамме, равных 0,5, прогноз, конечно, выглядит немного странно. Начиная с конца последнего месяца он внезапно возрастает, гораздо быстрее, чем ранее. Похоже, стоит оптимизировать параметры сглаживания.

Оптимизация одношаговой погрешности

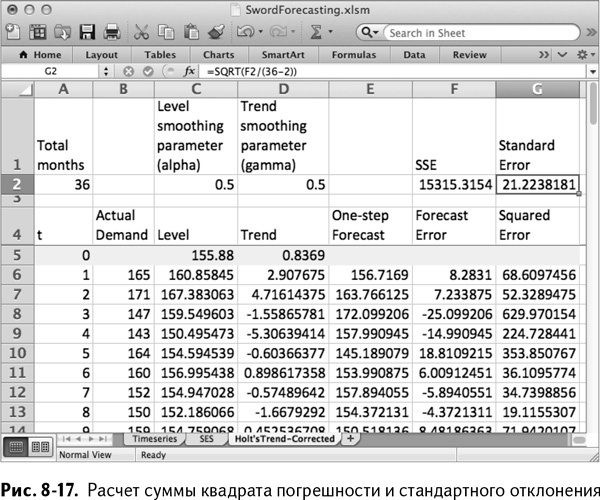
Точно так же, как и в случае с простым экспоненциальным сглаживанием, здесь нужно добавить квадрат погрешности прогноза в столбец G. В F2 и G2 можно рассчитать сумму квадратов погрешностей (отклонений) и стандартное отклонение для одношагового прогноза, в точности как и раньше. За исключением того, что в этот раз у модели два параметра сглаживания, так что придется разделить эту сумму на 36–2 перед извлечением из нее корня:

=SQRT(F2/(36–2))

=КОРЕНЬ(F2/(36–2))

Так получается лист, изображенный на рис. 8-17.

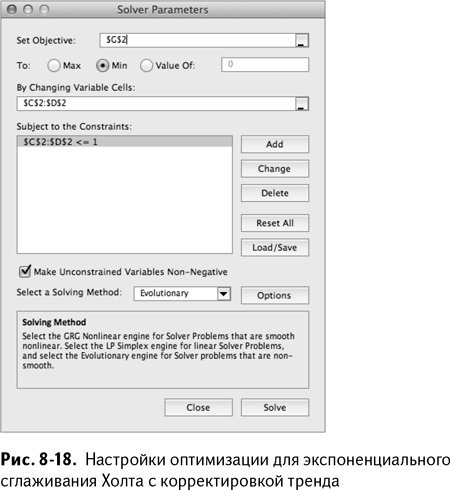
Настройки оптимизации идентичны таковым в простом экспоненциальном сглаживании. Единственное отличие – в этот раз вы оптимизируете оба параметра, альфу и гамму, вместе, как показано на рис. 8-18.

После запуска «Поиска решения» вы получите оптимальное значение альфы, равное 0,66, и гаммы, равное 0,05. Оптимальный прогноз показан на графике на рис. 8-19.

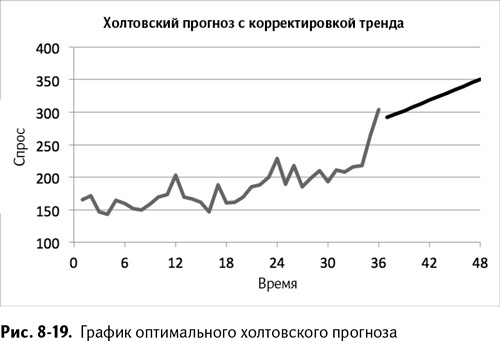
Тренд, который вытекает из вашего прогноза, – это пять дополнительных мечей, проданных за месяц. Этот тренд дублирует уже найденный вами ранее в предыдущей таблице, потому что сглаживание с корректировкой тренда ценит более поздние данные выше, и в этом случае спрос за недавнее время оказывается более «трендовым».

Обратите внимание, что этот прогноз начинается очень близко к прогнозу ПЭС для месяца 37–290 против 292. Но довольно быстро прогноз с корректировкой тренда начинает расти вместе с трендом, как вы и предполагали.

Так мы закончили? Взгляд на автокорелляции

Все ли возможное мы сделали? Все ли учли?

Есть один способ испытать вашу прогностическую модель на прочность – проверить погрешности одного шага вперед. Если эти отклонения случайны, то вы хорошо поработали. Но если найдется спрятанная в них закономерность – что-то вроде повторяющегося поведения на регулярных интервалах – возможно, в данных о спросе есть сезонный фактор, который мы не учли.

Под закономерностью я понимаю следующее: если взять погрешность и поместить ее рядом с ней же, но взятой за следующий месяц, или через два месяца, или даже 12 – будет ли она меняться синхронно? Эта концепция погрешности, коррелирующей с собственной версией за другой период, называется автокорреляцией («авто-» по-гречески означает «само-». Отличная, кстати, приставка для слива лишних гласных в «Эрудите»).

Так что начнем с создания нового листа под названием Holt’s Autocorrelation. Вставьте туда месяцы с 1 по 36 вместе с их одношаговыми погрешностями из холтовского прогноза – в столбцы А и В.

Под погрешностями в В38 рассчитайте среднюю погрешность. Получившийся лист показан на рис. 8-20.

В столбце С рассчитайте отклонения каждой погрешности в столбце В от среднего в В38. Эти отклонения одношаговых погрешностей от средней – то «пространство», где закономерности могут поднимать свои страшненькие головы. К примеру, возможно, что каждый декабрь погрешность прогноза значительно больше средней – и такая сезонная закономерность обнаружится в этих цифрах.

Итак, в С2 рассчитаем отклонение погрешности в В2 от средней:

=B2-B$38

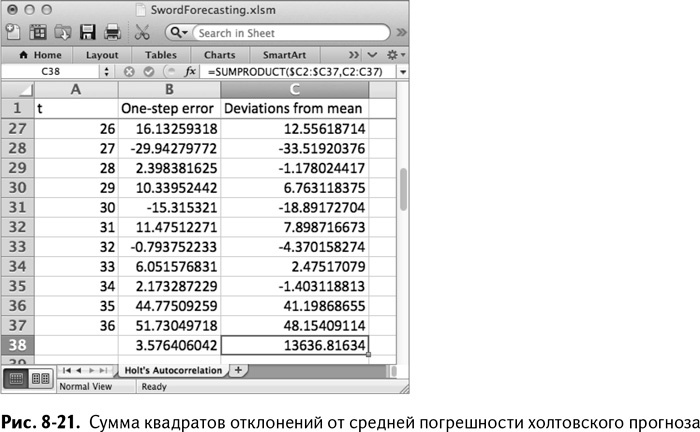
Затем можно растянуть эту формулу вниз, чтобы получить все отклонения. В ячейке С38 рассчитаем сумму квадратов отклонений:

=SUMPRODUCT($C2:$C37,C2:C37)

=СУММПРОИЗВ($C2:$C37,C2:C37)

Так получается таблица, изображенная на рис. 8-21.

Теперь поместим в столбец D отклонения погрешностей со сдвигом на месяц. Назовите столбец D «1». Ячейку D2 можете оставить пустой, а в D3 поместить

=С2

А теперь просто растяните эту формулу до D37, оказавшегося равным С36. Таким образом получается таблица, изображенная на рис. 8-22.

Чтобы сдвинуть отклонения на 2 месяца, просто выделите D1:D37 и перетяните в столбец Е. Точно так же можно сдвинуть погрешности на 12 месяцев – просто протащить выделенную область до столбца О. Элементарно! У вас получилась каскадная матрица сдвинутых отклонений погрешности, как показано на рис. 8-23.

Теперь, имея эти сдвиги, подумайте о том, что может значить для одного из этих столбцов «синхронное движение» со столбцом С. Возьмем, к примеру, сдвиг на 1 месяц в столбце D. Если эти два столбца синхронны, то число, отрицательное в одном из них, должно быть отрицательно и в другом. Собственно, и положительное должно быть таковым в обоих столбцах. Это означает, что произведение двух столбцов в результате будет иметь много положительных значений (отрицательное значение, умноженное на отрицательное, дает положительное, как и положительное, умноженное на положительное).

Сложите эти произведения. Чем ближе окажется сумма (SUMPRODUCT/СУММПРОИЗВ) столбца со сдвигом исходных отклонений к сумме квадратов отклонений в С38, тем более синхронны, более коррелированы сдвинутые погрешности будут к исходным.

Также вы можете получить негативную автокорелляцию, в которой сдвинутые отклонения становятся отрицательными, независимо от того, положительны исходные значения или отрицательны. SUMPRODUCT/СУММПРОИЗВ в этом случае будет довольно большим отрицательным числом.

Начнем с растягивания формулы SUMPRODUCT($C2:$C37,C2:C37)/ СУММПРОИЗВ($C2:$C37,C2:C37) в ячейке С38 вправо до столбца О. Обратите внимание на то, как абсолютная ссылка на столбец С сохраняет его на месте. У вас появляется SUMPRODUCT/СУММПРОИЗВ каждого столбца со сдвигом и исходного столбца, как показано на рис. 8-24.

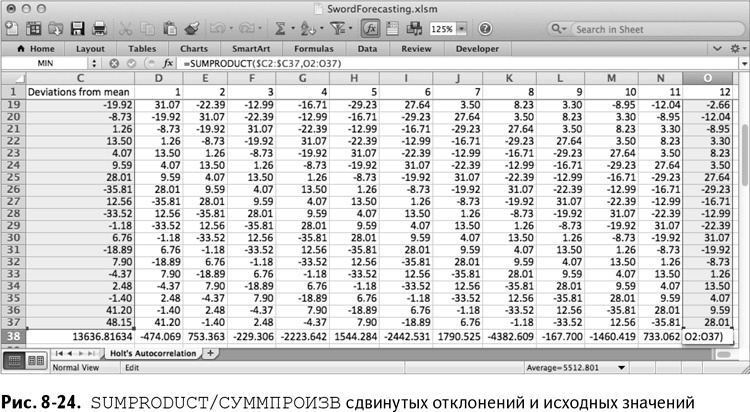
Теперь рассчитайте автокорреляцию данных со сдвигом на месяц: SUMPRODUCT/СУММПРОИЗВ отклонений сдвига, разделенная на сумму квадратов отклонений в С38.

Для примера можно рассчитать автокорреляцию сдвига на один месяц в ячейке С40:

=D38/$C38

Растянув ее по горизонтали, можно получить автокорреляцию для каждого сдвига.

Теперь выделите D40:О40 и вставьте столбчатую диаграмму, как показано на рис. 8-25 (кликните правой клавишей мышки на серии данных и отформатируйте их, чтобы столбики диаграммы стали прозрачнее и номера месяцев лучше читались под осью). Эта столбчатая диаграмма называется коррелограммой, (круто, да?). Она показывает автокорреляции для каждого сдвига на месяц до самого конца года.

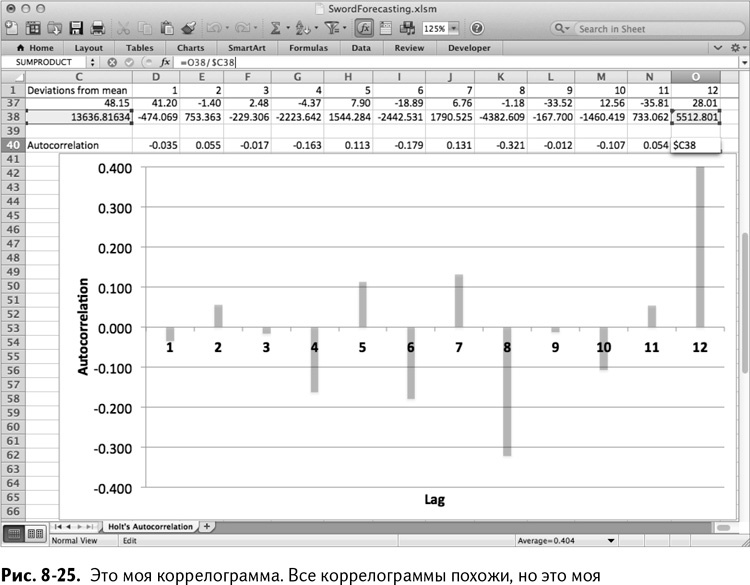
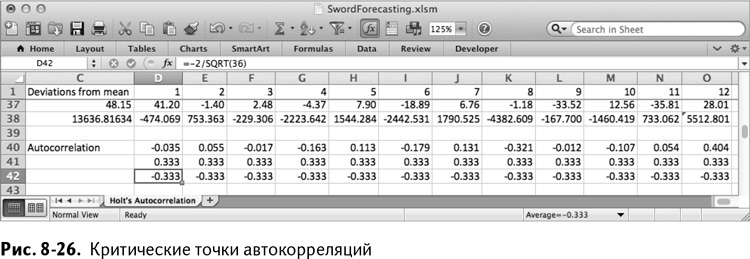
Какие автокорреляции нам важны? Как правило, все автокорреляции, большие, чем 2/корень из количества точек данных, что в нашем случае будет 2/√36 = 0,333. Также нас интересуют отрицательные автокорреляции меньше –0,333.

Посмотрите на эту диаграмму автокорреляций, находящихся выше и ниже критических значений. В прогнозировании на коррелограмме принято изображать критические значения пунктирной линией. Из любви к красивым картинкам я, так и быть, покажу, как это сделать здесь.

В ячейку D42 добавьте =2/SQRT(36)/=2/КОРЕНЬ(36) и растяните вправо до столбца О. В D43 сделайте то же самое, только с отрицательным значением: =–2/SQRT(36)/=–2/КОРЕНЬ(36) и тоже растяните вправо до О. Так получаются критические точки автокорреляций, показанные на рис. 8-26.

Кликните правой клавишей мышки на столбчатой диаграмме и выберите «Выбрать данные». В выплывшем окошке нажмите кнопку «Добавить», чтобы создать новые серии данных.

Для первой из них выберите промежуток D42:О42 для оси у. А для второй – D43:О43. Это добавит новые столбцы на диаграмму.

Правый щелчок на каждой из этих новых серий столбцов даст возможность изменить тип отображения данных на линейную диаграмму. Затем кликните правой кнопкой мыши на эти линии и выберите «Формат данных». Переключитесь на линию (тип линии в некоторых версиях Excel) в выплывшем окне. Здесь вы можете сделать свою линию пунктирной, как показано на рис. 8-27.

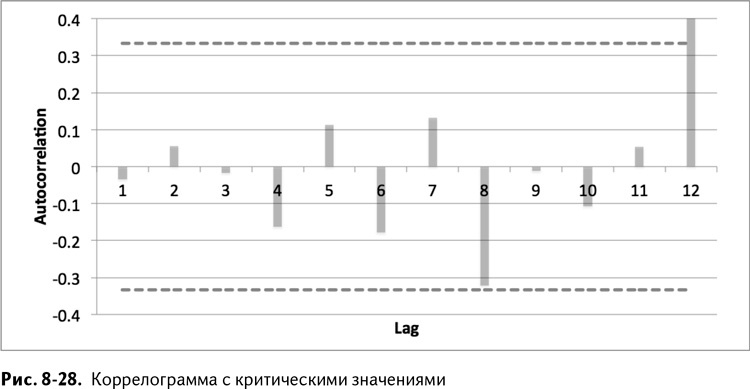
Таким образом получается коррелограмма с пунктирными критическими значениями. Она изображена на рис. 8-28.

И что же мы видим?

Совершенно точно есть одна автокорреляция выше критического значения, и это 12 месяцев.

Погрешность, сдвинутая на год, коррелирует сама с собой. Это означает 12-месячный сезонный цикл. И это неудивительно. Если вы посмотрите на график спроса во вкладке Timeseries, то окажется, что есть пики спроса на каждое Рождество и провалы в апреле-мае.

Вам нужна такая техника прогнозирования, которая способна учитывать сезонность. Кроме того, существует аналогичная техника экспоненциального сглаживания.

Назад: Возможно, у вас есть тренд

Дальше: Мультипликативное экспоненциальное сглаживание Холта – Винтерса