Достаточно беглого взгляда на этот график, чтобы понять несколько вещей. Во-первых, простое экспоненциальное сглаживание – это прямая линия, уровень. Но если посмотреть на данные о спросе за прошедшие 36 месяцев, то окажется, что он поднялся. Похоже на восходящий тренд, особенно в конце.

Наши глаза, определенно, не врут, но все же как это доказать?

Для доказательства достаточно подогнать линейную регрессию под данные спроса и выполнить тест на соответствие критерию Стьюдента на подъеме этой линии тренда, в точности как в главе 6.

Если уклон линии ненулевой и статистически значимый (в проверке по критерию Стьюдента величина р менее 0,05), то можете быть уверены: у данных есть тренд. Если в последнем предложении вы не видите никакого смысла, загляните в раздел главы 6 о статистических тестах.

Переключитесь во вкладку Timeseries вашей электронной таблицы для выполнения проверки тренда.

В главе 6 я испытывал ваш характер, заставляя выполнять проверки критериев Стьюдента и Фишера вручную. Но я не зверь, чтобы подвергать вас этому испытанию вторично.

В этой главе для подгонки линейной регрессии, а также для проверки уклона, расчета стандартного отклонения коэффициента уклона и количества степеней свободы (если не понимаете эти термины – загляните в главу 6) мы будем использовать функцию LINEST/ЛИНЕЙН, встроенную в Excel. Затем можно будет рассчитать статистику Стьюдента и пропустить ее через функцию TDIST/СТЬЮДРАСП, как описано в главе 6.

Если вы никогда раньше не пользовались функцией LINEST/ЛИНЕЙН, ознакомьтесь со справочным материалом Excel по этой функции. Вы задаете LINEST/ЛИНЕЙН данные зависимых переменных (спроса в столбце В) и независимых (у вас только одна независимая переменная, и это – время в столбце А).

Отметив «Истина», вы даете функции понять, что свободный член надо подгонять как часть линии регрессии, и еще раз – чтобы получить детализированный отчет по стандартному отклонению и R-квадрату. После этого линейную регрессию на листе Timeseries можно запустить следующим образом:

=LINEST(B2:B37,A2:A37,TRUE,TRUE)

=ЛИНЕЙН(B2:B37,A2:A37,ИСТИНА,ИСТИНА)

Эта формула вернет уклон линии регрессии, потому что LINEST/ЛИНЕЙН – формула массива. LINEST/ЛИНЕЙН возвращает всю статистику регрессии в массиве, чтобы вытряхнуть все содержимое в выбранную область таблицы. Вы также можете воспользоваться формулой INDEX/ИНДЕКС для LINEST/ЛИНЕЙН, чтобы вытащить только интересующие вас значения одно за другим.

Например, первые компоненты линии регрессии, которые выдает LINEST/ЛИНЕЙН, – это коэффициенты регрессии, так что можно рассчитать уклон регрессии в ячейке В39 таблицы Timeseries, пропуская LINEST/ЛИНЕЙН через INDEX/ИНДЕКС:

=INDEX(LINEST(B2:B37,A2:A37,TRUE,TRUE),1,1)

=ИНДЕКС(ЛИНЕЙН(B2:B37,A2:A37,ИСТИНА,ИСТИНА),1,1)

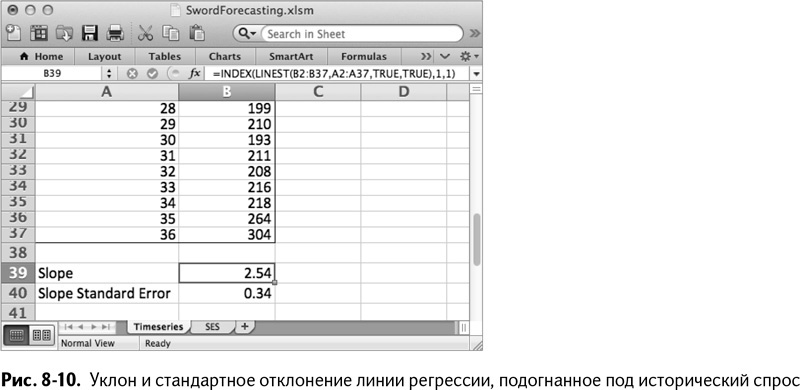
Получается уклон, равный 2,54, что означает тренд линии регрессии к повышению спроса на 2,54 дополнительных меча в месяц. То есть уклон действительно есть. Но значим ли он статистически?

Чтобы проверить уклон критерием Стьюдента, нужно узнать стандартное отклонение уклона и количество степеней свободы регрессии. LINEST/ЛИНЕЙН помещает значения стандартного отклонения в строку 2, столбец 1 массива результатов. К примеру, в В40 вы можете это написать как:

=INDEX(LINEST(B2:B37,A2:A37,TRUE,TRUE),2,1)

=ИНДЕКС(ЛИНЕЙН(B2:B37,A2:A37,ИСТИНА,ИСТИНА),2,1)

Единственное отличие от вычисления уклона заключается в том, что вместо ряда 1 столбца 1 мы задаем формуле INDEX/ИНДЕКС строку 2 столбец 1 и находим стандартное отклонение.

Стандартное отклонение уклона получается равным 0,34. Таблица на этом этапе показана на рис. 8-10.

Точно так же функция LINEST/ЛИНЕЙН знает, что степени свободы регрессии помещены в строку 4 столбца 2 итогового массива. Поэтому в В41 их можно вычислить следующим образом:

=INDEX(LINEST(B2:B37,A2:A37,TRUE,TRUE),4,2)

=ИНДЕКС(ЛИНЕЙН(B2:B37,A2:A37,ИСТИНА,ИСТИНА),4,2)

У вас должно получиться 34 степени свободы (как отмечено в главе 6, они рассчитываются как 36 точек данных минус 2 коэффициента линейной регрессии).

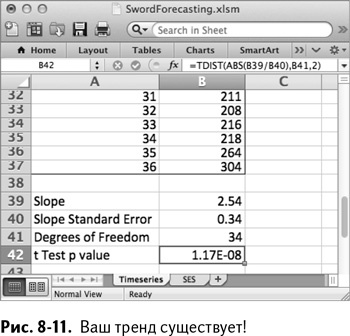
Теперь известны все три значения для проверки критерием Стьюдента статистической значимости вашего подогнанного тренда. Так же, как и в 6 главе, вы можете вычислить статистику этого критерия как абсолютную величину уклона, разделенную на стандартное отклонение уклона. Рассчитайте величину р для этой статистики из распределения Стьюдента с 34 степенями свободы, воспользовавшись функцией TDIST/СТЬЮДРАСП в В42:

=TDIST(ABS(B39/B40),B41,2)

=СТЬЮДРАСП(ABS(B39/B40),B41,2)

Функция выдает значение р, близкое к 0, намекая на то, что если бы тренд был не существующим в реальности (уклон 0), то ни при каких условиях мы бы не получили настолько отличающийся от регрессии уклон. Это показано на рис. 8-11.

Поздравляю! У вас есть тренд. Осталось включить его в прогноз.