Книга: Много цифр. Анализ больших данных при помощи Excel
Назад: Знакомство с временной последовательностью данных
Дальше: Возможно, у вас есть тренд
Медленный старт с простым экспоненциальным сглаживанием
Методы экспоненциального сглаживания основываются на прогнозировании будущего по данным из прошлого, где более новые наблюдения весят больше, чем старые. Такое взвешивание возможно благодаря константам сглаживания. Первый метод экспоненциального сглаживания, который мы опробуем, называется простым экспоненциальным сглаживанием (ПЭС, simple exponential smoothing, SES). Он использует лишь одну константу сглаживания.
При простом экспоненциальном сглаживании предполагается, что ваш временной ряд данных состоит из двух компонентов: уровня (или среднего) и некоей погрешности вокруг этого значения. Нет никакого тренда или сезонных колебаний – есть просто уровень, вокруг которого «висит» спрос, тут и там окруженный небольшими погрешностями. Отдавая предпочтение более новым наблюдениям, ПЭС может явиться причиной сдвигов этого уровня. Говоря языком формул,
Спрос в момент времени t = уровень + случайная погрешность около уровня в момент времени t
Самое последнее приближение уровня служит прогнозом на будущие периоды времени. Если вы обсчитываете месяц 36, каким будет хорошее приближение на период 38? Самое последнее приблизительное значение уровня. А на 40? Уровень. Все просто – ведь это простое экспоненциальное сглаживание.
Так как же найти приблизительное значение уровня?
Если принять все временные значения как имеющие одинаковую ценность, то следует просто вычислить их среднее значение.
Это среднее задаст вам уровень, и вы будете предсказывать будущее, говоря себе: «Будущий спрос – это средний спрос прошлого». Некоторые компании поступают именно так. Я видел ежемесячные прогнозы, в которых будущий спрос равнялся среднему за прошедшие месяцы последних нескольких лет. Плюс «поправочный коэффициент» смеха ради. Да-да, прогнозирование зачастую делается настолько криворуко, что даже крупные публичные компании до сих пор используют архаизмы вроде «поправочного коэффициента». Фу!
Но когда уровень изменяется во времени, то нет нужды одинаково оценивать каждую точку прошлого, как при использовании среднего. Должны ли все данные с 2008 по 2013 год весить одинаково, чтобы спрогнозировать 2014-й? Возможно, но для большей части компаний, вероятно, это не так. Так что нам нужно приблизительное значение уровня, которое дает больший вес недавним наблюдениям спроса.
Давайте вместо этого подумаем о расчете уровня, пройдясь по точкам данных по порядку и обновляя его по мере продвижения. Для начала решим, что исходное значение уровня – это среднее от нескольких последних точек данных. В этом случае выберите значения первого года. Назовите их исходным уровнем, уровень0:
уровень0= среднее значение спроса за первый год (месяцы 1–12)
Для спроса на мечи он равен 163.
Теперь о том, как работает экспоненциальное сглаживание. Даже при том, что вы знаете спрос за месяцы с 1 по 36, вам нужно взять компоненты вашего самого последнего прогноза и использовать их для предсказания на месяц вперед с помощью полного ряда данных.
Мы используем уровень0 (163) как прогноз спроса на месяц 1.
Предсказав период 1, вы шагаете вперед во времени от периода 0 к периоду 1. Текущий спрос равен 165, то есть он вырос на 2 меча. Стоит обновить приближение исходного уровня. Уравнение простого экспоненциального сглаживаня выглядит так:
уровень1 = уровень0 + несколько процентов × (спрос1 – уровень0)
Обратите внимание, что (спрос1 – уровень0) – ошибка, которую вы получаете, когда предсказываете период 1 с использованием первоначального уровня. Шаг вперед:
уровень2 = уровень1 + несколько процентов × (спрос2 – уровень1)
И еще один:
уровень3 = уровень2 + несколько процентов × (спрос3 – уровень2)
Теперь выясним, сколько процентов погрешности вы готовы заложить в уровень – это будет константа сглаживания, и для уровня ее название – альфа (так исторически сложилось). Это может быть любое число от 0 до 100 % (от 0 до 1).
Если вы сделаете альфу равной 1, то получится, что погрешностью является все, означающее, что уровень текущего периода равен спросу на текущий период.
Если сделать альфу равной 0, то в первом прогнозе уровня не останется совсем никакой коррекции погрешности.
Наверное, нам нужно что-то между этими двумя крайностями, но выбирать лучшее значение альфы вы научитесь позже.
Пока же проведите это вычисление для разных моментов времени:
уровеньтекущий период = уровеньпредыдущий период + альфа ×× (спростекущий период – уровень предыдущий период)
В итоге вы имеете финальное приближение уровня – значение уровень36, где последние наблюдения спроса весят больше, потому что их поправки на погрешность не умножались с каждым следующим значением альфа:
уровень36 = уровень35 + альфа × (спрос36 – уровень35)
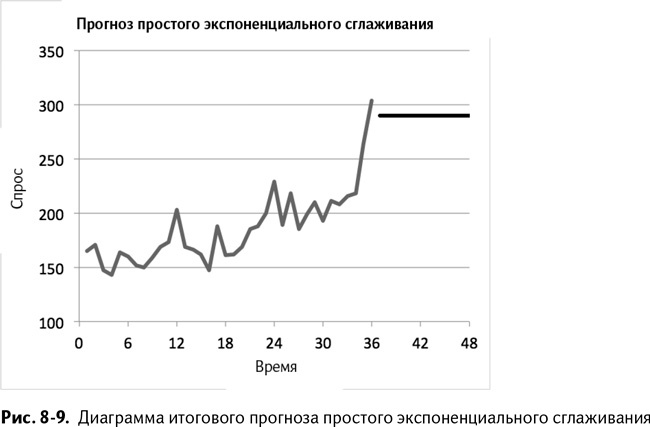
Это итоговое приближение уровня – то, что вы будете использовать как прогноз на будущие месяцы. Спрос за месяц 37? Ну, это просто уровень36. А как насчет месяца 40? Уровень36. Месяц 45? Уровень36. У вас есть картинка. Итоговое приближение уровня – просто лучшее из тех, что у вас есть на будущее, так что его вы и используете.
Давайте взглянем на него в таблице.
Настраиваем прогноз простого экспоненциального сглаживания
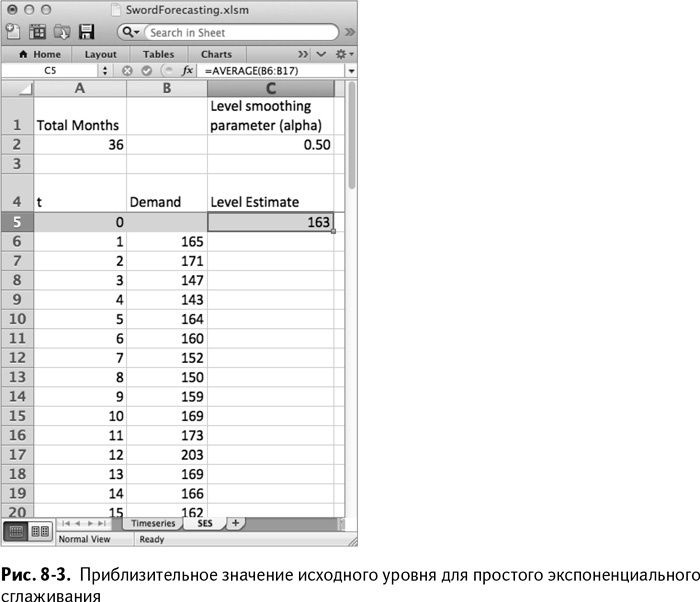
Первое, что нужно сделать, – это создать новый лист в документе под названием SES. Вставьте временной ряд данных в столбцы А и В, начиная со строки 4, чтобы оставить немного места наверху для значений альфа. Вы можете ввести количество месяцев, которое у вас есть (36) в ячейку А2, а исходное значение альфа – в С2. Я начну с 0,5, потому что это число между 0 и 1 и оно мне нравится.
Поместите расчет уровня в столбец С. Нужно вставить новую строку 5 во временной ряд данных вверху таблицы для исходного приближения уровня в момент времени 0. В С5 используйте следующий расчет:
=AVERAGE(B6:B17)
=СРЗНАЧ(B6:B17)
Эти средние значения данных за первый год дают исходный уровень. Таблица с ними выглядит так, как показано на рис. 8–3.
Добавление одношагового прогноза и погрешности
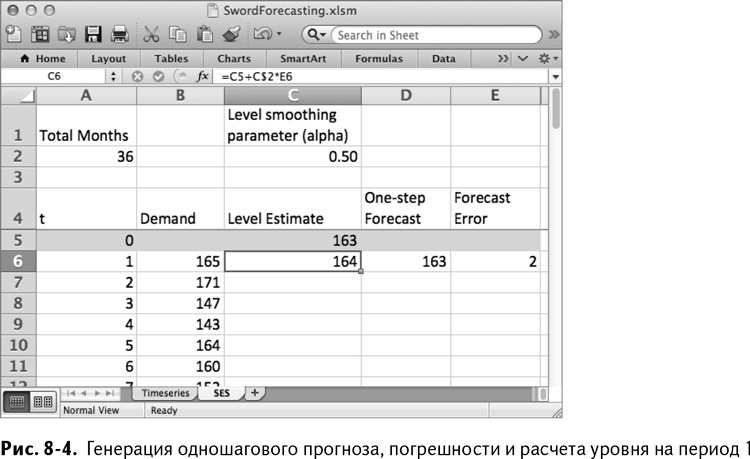
Теперь, когда вы добавили в последовательность значения первого уровня, можно идти вперед во времени с помощью формулы ПЭС, описанной в предыдущем разделе. Для этого добавьте еще два столбца: столбец одношагового прогноза (D) и погрешности прогноза (Е). Одношаговый прогноз за период времени 1 – это уровень0 (ячейка С5), а расчет погрешности – это разница текущего спроса и прогноза:
=B6-D6
Приблизительное значение уровня за период 1 – это предыдущий уровень, с поправкой на альфу, умноженное на погрешность, то есть:
=C5+C$2*E6
Обратите внимание, что у меня перед альфой стоит значок $, поэтому при распространении формулы на всю таблицу абсолютные ссылки на строку позволяют альфе оставаться собой. Таким образом получается лист, изображенный на рис. 8–4.
Рястяните
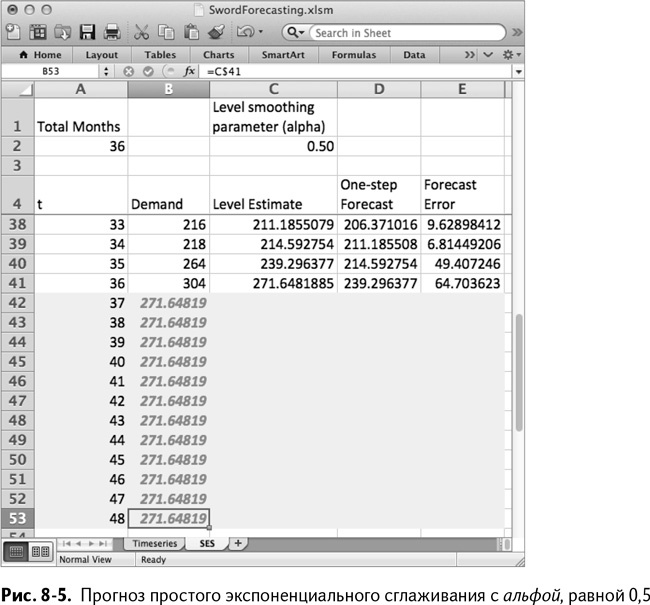
Вы будете смеяться, но сделано уже практически все. Просто растяните С6:Е6 вниз на все 36 месяцев и – вуаля! – у вас есть уровень.
Добавим месяцы 37–48 в столбец А. Прогноз на следующие 12 месяцев – это просто уровень36. Так что в В42 можно добавить только
=C$41
в качестве прогноза и оттянуть его на весь следующий год.
Таким образом получается прогноз, равный 272, как показано на рис. 8–5.
Но неужели нельзя сделать что-то получше? Сейчас наш способ оптимизации прогноза – установка значений альфы: чем альфа больше, тем меньше нам важны старые данные о спросе.
Оптимизация одношаговой погрешности
Точно так же, как вы оптимизировали сумму квадратов отклонений во время подгонки регрессии в главе 6, можно найти лучшую константу сглаживания для прогноза путем минимизации суммы квадратов отклонений (погрешностей) для прогнозирования предстоящего периода.
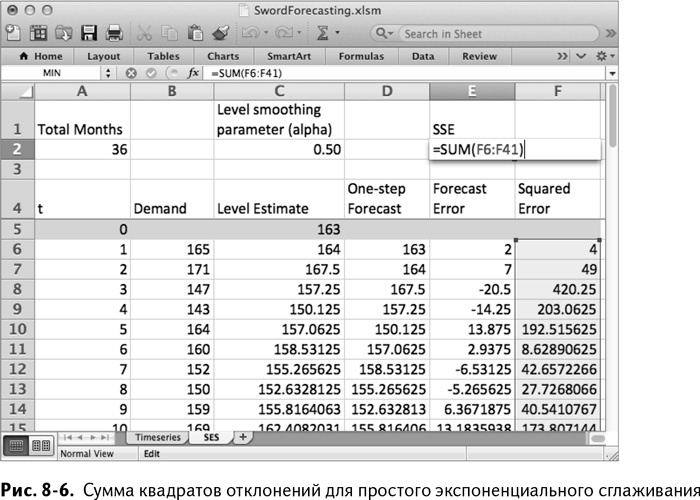
Добавим расчет квадрата отклонения в столбец F – это просто значение из столбца Е, возведенное в квадрат, – и растянем этот расчет на все 36 месяцев, а затем сложим их все в ячейке Е 2, чтобы получить сумму квадратов отклонений (СКО). Таким образом у нас получается лист, изображенный на рис. 8–6.
Также в нашу таблицу нужно добавить само стандартное отклонение– в ячейку F2. Стандартное отклонение – это квадратный корень из СКО, разделенный на 35 (36 месяцев за вычетом количества сглаживающих параметров модели, которое для простого экспоненциального сглаживания равно 1).
Стандартное отклонение – это приблизительное значение стандартного распределения для одношаговой погрешности (отклонения). Вы уже встречались с ним в главе 4. Это просто оценка распределения погрешности.
Если ваша прогностическая модель отлично подогнана, то среднее значение погрешности будет 0. Это, скажем так, непредвзятый прогноз. Он настолько же преувеличивает спрос, насколько и преуменьшает. Стандартное отклонение численно выражает распределение вокруг 0, если прогноз непредвзятый.
В ячейке F2 стандартное отклонение вычисляется как:
=SQRT(E2/(36–1)
=КОРЕНЬ(E2/(36–1)
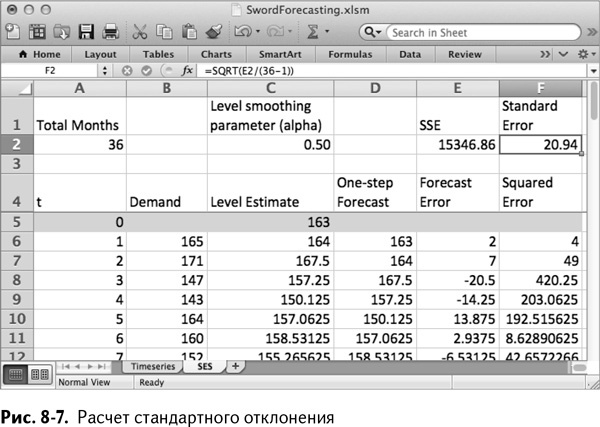
Для альфы, равной 0,5, оно получается равным 20,94 (рис. 8–7). Вспомнив правило 68–95–99,7 из обсуждения нормального распределения в главе 4, вы поймете, что 68 % погрешностей одношагового прогноза должны оказаться меньше 20,94 и больше –20,94.
Теперь ваша задача – сжать это распределение насколько возможно, найдя подходящее значение альфы. Попробуйте несколько разных значений, используя «Поиск решения» в который раз в этой книге.
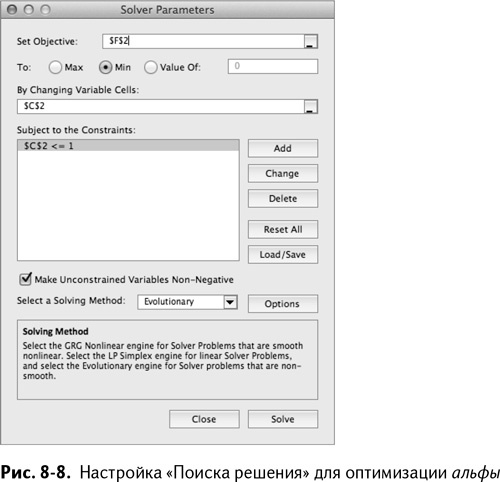
Настройка «Поиска решения» для этой операции чрезвычайно проста. Откройте опцию, установите целевую функцию – стандартное отклонение в ячейке F2, и переменную решения – альфа в С2, добавьте ограничение, что С2 должна быть меньше 1, и поставьте галочку в поле, указывающем, что решение должно быть неотрицательным. Рекурсивные расчеты уровня, входящие в каждый расчет погрешности прогноза, очень нелинейны, поэтому для оптимизации альфы нам придется воспользоваться эволюционным алгоритмом.
Настройка «Поиска решения» должна выглядеть так, как показано на рис. 8–8. Нажав «Выполнить» вы получаете значение альфы, равное 0,73, что дает нам новое стандартное отклонение 20,39. Не такое уж кардинальное улучшение!
А теперь графика!
Лучший способ проверить наш прогноз – это нарисовать его диаграмму рядом с графиком данных о спросе в прошлом и посмотреть, как спрогнозированный спрос отличается от реального. Мне нравится вид простой диаграммы Excel. Для начала выберите А6:В41, где расположены наши исторические данные, и простую линейную диаграмму из вариантов, предложенных Excel.
Добавив график, кликните на нем правой кнопкой мыши, выберите «Выбрать данные» и вставьте туда новую серию свежепредсказанных значений А42:В53. Если хотите, добавьте также названия осей, после чего у вас получится что-то похожее на рис. 8–9.