Книга: Много цифр. Анализ больших данных при помощи Excel
Назад: Экспоненциальное сглаживание Холта с корректировкой тренда
Дальше: Подытожим
Мультипликативное экспоненциальное сглаживание Холта – Винтерса
Мультипликативное экспоненциальное сглаживание Холта – Винтерса является логическим продолжением сглаживания Холта с корректировкой тренда. Оно учитывает уровень, тренд и необходимость подгонки спроса вверх или вниз на регулярной основе «в угоду» сезонным флуктуациям. Сезонные колебания не обязательно имеют годовой цикл, как в нашем примере. В случае MailChimp мы имеем периодические колебания спроса каждый четверг (похоже, четверг считается отличным днем для отправки маркетинговых писем). С помощью Холта – Винтерса мы можем учесть этот недельный цикл.
В большинстве случаев вы не можете просто взять и прибавить или отнять от спроса какую-либо фиксированную сезонную величину ради подгонки прогноза. Если ваш бизнес растет от продаж в 200 мечей до 2000 каждый месяц, добавление 20 штук в модель в качестве подгонки под рождественский всплеск спроса – не очень хорошая идея. Нет, сезонные изменения обычно должны быть результатом умножения. Вместо прибавления 20 мечей, возможно, стоило бы умножить прогноз на 120 %. Вот почему метод называется мультипликативным (от multiplicate – умножать). Вот как этот прогноз представляет себе спрос:
Спрос в момент t = (уровень + t × тренд) × сезонная поправка для момента t × все оставшиеся нерегулярные поправки, которые мы не можем учесть
Таким образом, теперь у вас есть структура тренда и уровня, идентичная той, что была в холтовском сглаживании с корректировкой тренда. А поскольку мы не в силах учесть нерегулярные колебания спроса, такие как божья воля, то не станем и пытаться.
Сглаживание Холта – Винтерса также называют тройным экспоненциальным сглаживанием, потому что, как вы, наверно, сами догадались, у него три сглаживающих параметра. Здесь, кроме, знакомых нам альфы и гаммы, также присутствует сезонный фактор с обновленным уравнением. Он называется дельта.
Три уравнения корректировки погрешности немного сложнее, чем то, с чем вы ранее имели дело, но есть и много общего.
Перед тем, как начать, я хочу прояснить одну вещь. Вы использовали уровни и тренды предыдущего периода, чтобы предсказать и скорректировать следующий, – но при сезонных корректировках можно на него и не оглядываться. Нас больше интересует приближение фактора корректировки для конкретной точки цикла. В нашем случае это на 12 периодов раньше.
Это значит, что если сейчас месяц 36 и вы прогнозируете на 3 следующих месяца, до 39, то прогноз будет выглядеть так:
Прогноз на месяц 39 = (уровень36 + 3 × тренд36) × сезонность27
Да-да, все верно, там написано сезонность27. Это самое последнее приближение сезонной корректировки для марта. Нельзя использовать сезонность36, потому что это – декабрь.
Покопаемся в обновлениях уравнений, начиная с этого уровня. Теоретически вам нужен только исходный уровень0 и тренд0, но на самом деле потребуется двенадцать исходных сезонных факторов, от сезонности–11 до сезонности0.
К примеру, обновленное уравнение для уровня1 основано на исходном сезонном приближении для января:
уровень1 = уровень0 + тренд0 + альфа × (спрос1 – (уровень0 + тренд0) × сезонность − 11) /сезонность − 11
В этом расчете уровня многие компоненты вам знакомы. Текущий уровень – это предыдущий уровень плюс предыдущий тренд (точно так же, как и в двойном экспоненциальном сглаживании) плюс альфа, умноженная на одношаговую погрешность (спрос1 – (уровень0 + тренд0) × сезонность − 11), где погрешность получает сезонную корректировку, будучи разделенной на сезонност ь–11.
Таким образом мы продвигаемся вперед во времени, и следующий месяц будет выглядеть так:
уровень2 = уровень1 + тренд1 + альфа × (спрос2 − (уровень1 + тренд1) × сезонность − 10)/сезонность − 10
Общий уровень будет иметь такую формулу для расчета:
уровеньтекущий период = уровеньпредыдущий период + трендпредыдущий период + альфа × (спростекущий период – (уровеньпредыдущий период + трендпредыдущий период) × сезонностьпоследний релевантный период) / сезонностьпоследний релевантный период
Тренд обновляется соответственно уровню в точности так же, как и при двойном экспоненциальном сглаживании:
трендтекущий период = трендпредыдущий период + гамма + альфа × (спростекущий период – (уровеньпредыдущий период + трендпредыдущий период) × сезонностьпоследний релевантный период) / сезонностьпоследний релевантный период
Как и при двойном экспоненциальном сглаживании, текущий тренд – это предыдущий тренд плюс гамма, умноженная на погрешности, включенные в уравнение обновления уровня.
А теперь – уравнение обновления сезонного фактора. Оно не похоже на уравнение обновления тренда, разве что корректирует последний релевантный сезонный фактор с помощью дельты, умноженной на погрешность, которую обновления уровня и тренда игнорировали:
сезонностьтекущий период = сезонностьпоследний релевантный период + дельта × (1 – альфа) × (спростекущий период – (уровеньпредыдущий период + трендпредыдущий период) × сезонностьпоследний релевантный период) / (уровеньпредыдущий период + тренд предыдущий период)
В этом случае вы не только обновляете корректировку сезонности соответствующим фактором за 12 предшествующих месяцев, но также и вкладываете в нее дельту, умноженную на все неучтенные погрешности, валяющиеся обрезками на полу мастерской после обновления уровня. Обратите внимание: вместо того, чтобы сезонно корректировать погрешность, вы делите на значения предыдущего уровня и тренда. С помощью «корректировки уровня и тренда» одношаговой погрешности вы помещаете погрешность в ту же шкалу множителей, что и сезонные факторы.
Установка исходных значений уровня, тренда и сезонности
Установка исходных значений для ПЭС и двойного экспоненциального сглаживания происходила проще простого. Но теперь вам нужно выяснить, что в серии данных является трендом, а что – сезонностью. Установка исходных значений для этого прогноза (одного уровня, одного тренда и 12 сезонных корректирующих факторов) в этот раз немного труднее. Существуют простые (и неверные!) способы провести ее. Я покажу вам правильный метод инициализации Холта – Винтерса, при том что ваши исторические данные имеют как минимум объем в два сезонных цикла. В нашем случае есть объем данных в три цикла.
Вот что нужно сделать:
• Сгладить исторические данные методом скользящего среднего 2 × 12.
• Сравнить сглаженную версию временного ряда данных с оригиналом, чтобы получить приблизительную оценку сезонности.
• С помощью исходных приближений сезонности десезонировать исторические данные.
• Найти приближения уровня и тренда с помощью линии тренда десезонированных данных.
Для начала создайте новый лист и назовите его HoltWintersInitial. Затем вставьте в первые два столбца временную серию данных. Теперь нужно сгладить некоторые из этих данных с помощью скользящего среднего. Так как сезонность рассчитывается у нас в 12-месячных циклах, имеет смысл использовать среднее за 12 месяцев.
Что значит скользящее среднее за 12 месяцев?
Для расчета вы берете спрос за конкретный месяц и спрос за периоды до и после, и вычисляете среднее значение. Так утрамбовываются все странные всплески в серии.
Но со скользящим средним за 12 месяцев есть проблема. 12 – четное число. Если вы сглаживаете спрос за месяц 7, стоит ли считать его средним спросом с 1-го по 12-й месяц или со 2-го по 13-й? Иначе говоря, месяц 7 не совсем в середине. Середины нет!
Чтобы справиться с этим затруднением, нужно сгладить спрос с помощью «скользящего среднего 2 × 12», что является средним значением обоих вариантов – месяцев с 1 по 12 и со 2 по 13. (То же самое относится к любому четному числу временных периодов цикла. Если в вашем цикле нечетное количество периодов, часть «2×» скользящего среднего вам не нужна и вы можете вычислить простое скользящее среднее.)
А теперь обратите внимание: для первых шести месяцев данных и для шести последних такие вычисления вообще не представляются возможными. У вас нет данных за 6 месяцев ни с какой стороны. Все, что вы можете – это сгладить месяцы из середины последовательности данных (в нашем случае месяцы 7–30). Именно поэтому вам нужна последовательность данных длиной как минимум два года – чтобы в итоге сглаживать данные за год.
Таким образом, можно использовать эту формулу начиная с месяца 7:
=(AVERAGE(B3:B14)+AVERAGE(B2:B13))/2
=(СРЗНАЧ(B3:B14)+СРЗНАЧ(B2:B13))/2
Это среднее значение месяца 7 с 12 месяцами до и после него, за исключением того, что месяцы 1 и 13 учитываются как половина остальных месяцев. Такой учет имеет определенный смысл: так как эти месяцы, 1 и 13, приходятся на один и тот же календарный месяц, то, если бы мы считали каждый из них как один, в вашем среднем оказалось бы слишком много данных за январь.
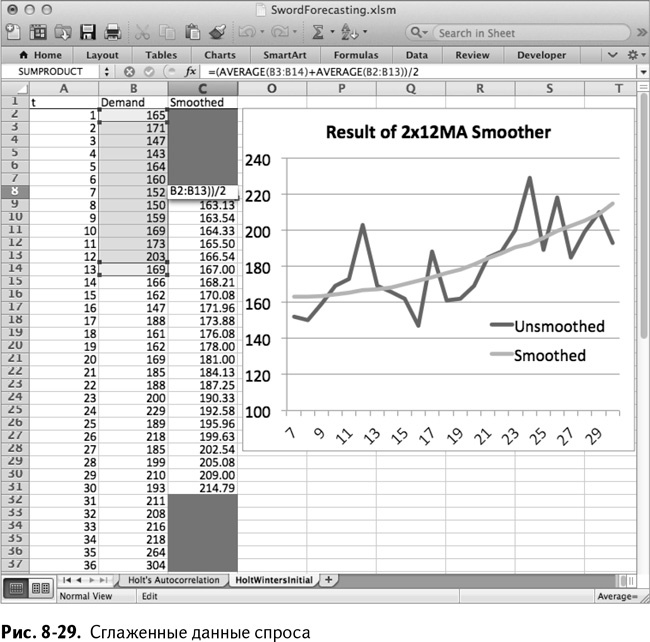
Растягивая эту формулу вниз до месяца 30 и помещая на простую линейную диаграмму и сглаженные данные, и оригинал, вы получаете лист, изображенный на рис. 8-29. На своей диаграмме я назвал их сглаженными (smoothed) и несглаженными (unsmoothed). После взгляда на сглаженную линию становится очевидным, что любые сезонные изменения, имеющиеся в данных, сглажены.
Теперь в столбце D разделите оригинальную величину на сглаженную и получите приблизительное значение сезонной поправки.
В8/С8
Полученную комбинацию растяните вниз до месяца 30. Обратите внимание на всплески в 20 % выше нормального спроса в месяцах 12 и 24 (декабрь), в то время как весной наблюдаются провалы.
Эта техника сглаживания дала вам две (для каждого фактора сезонности) точечные оценки. Давайте узнаем среднее значение этих двух факторов в столбце Е, что будет исходным сезонным фактором для Холта – Винтерса.
Например, в Е2, где находятся данные за январь, нужно взять среднее от двух значений спроса за январь из столбца D, ячеек D8 и D26. Так как сглаженные данные в столбце D начинаются от середины года, то растянуть формулу среднего нельзя. В Е8, где находятся данные за июль, нужно брать среднее от D8 и D20, к примеру.
Когда все эти 12 корректировок будут у вас в столбце Е, можно вычесть единицу из каждого из них в столбце F и отформатировать ячейки в проценты (выделить их и правым щелчком мыши вызвать меню, в котором выбрать «Формат ячеек»), чтобы увидеть, как эти факторы двигают спрос вверх или вниз каждый месяц. Вы можете даже вставить столбчатую диаграмму этих значений в таблицу, как показано на рис. 8-30.
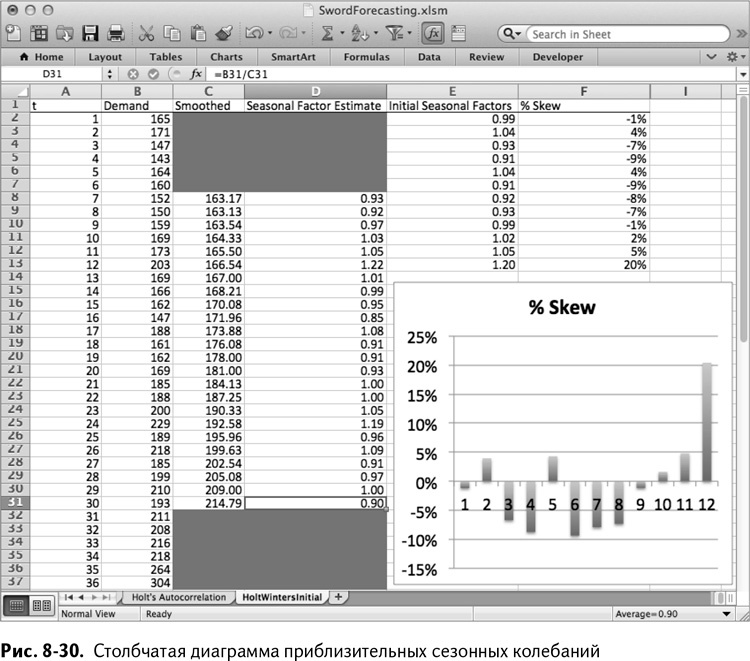
Теперь, когда у вас есть эти исходные сезонные корректировки, можно использовать их для десезонализации временной последовательности данных. Когда вся серия будет десезонализирована, можно провести через нее линию тренда, а затем использовать уклон и свободный член в качестве начального отрезка и тренда.
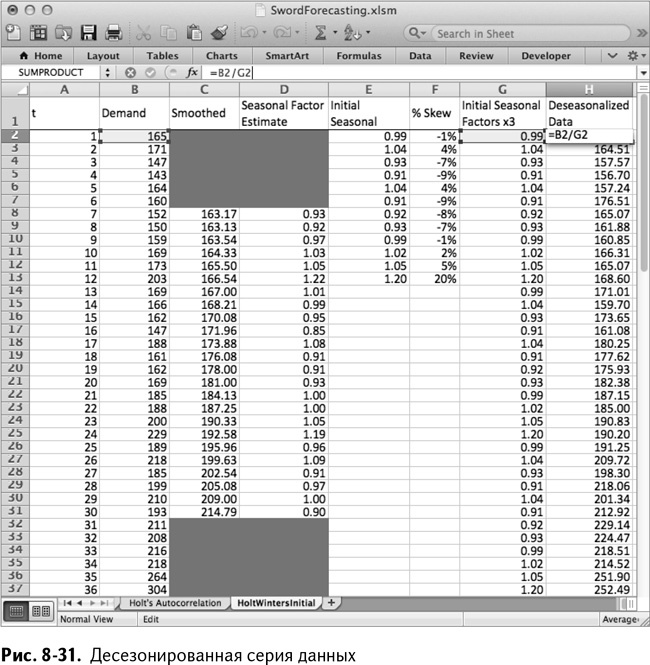
Для начала вставьте соответствующие значения сезонных корректировок за каждый месяц от G2 до G37. Фактически вы вставляете Е2:Е13 три раза подряд в столбец G (убедитесь, что вы вставляете только значения). В столбце Н разделите исходную серию данных из столбца В на сезонные факторы из столбца G, чтобы удалить приблизительный сезонный фактор из данных. Эта таблица показана на рис. 8-31.
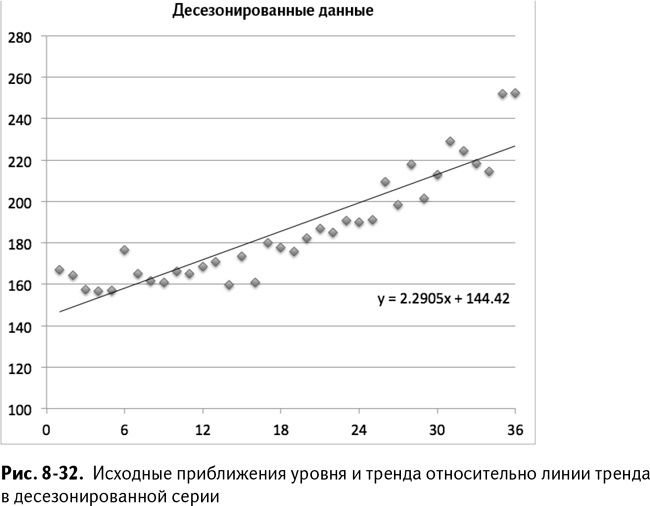
Теперь, как и на предыдущих листах, вам нужно вставить диаграмму столбца Н и провести на ней линию тренда. Отобразив уравнение этой линии на графике, вы получите исходное приближение тренда, равное 2,29 дополнительных проданных мечей в месяц, и исходное приближение уровня, равное 144,42 (рис. 8-32).
Приступим к прогнозу
Теперь, когда у вас есть исходные значения всех параметров, настало время создать новый лист под названием HoltWintersSeasonal, в строку 4 которого для начала нужно вставить серию данных, точно так же, как и в двух рассмотренных выше методах прогнозирования.
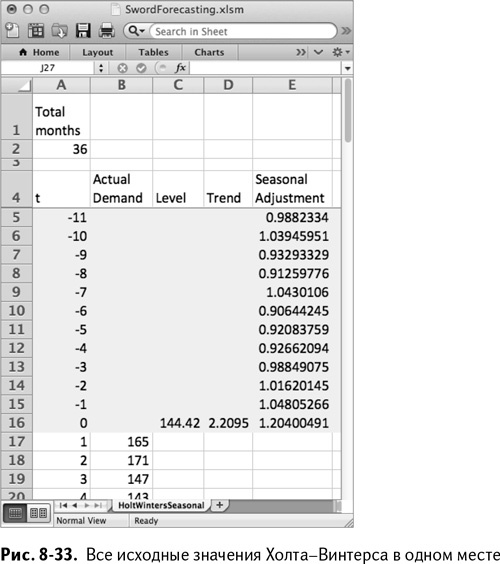
В столбцах C, D и E рядом с этой серией расположатся уровень, тренд и сезонные значения соответственно. Но на этот раз, в отличие от двух предыдущих, где нам нужно было вставить только одну пустую строку 5, мы вставляем пустые строки с 5 по 16 и нумеруем их по месяцам относительно текущего – от –11 до 0 в столбце А. Затем исходные значения из предыдущего листа можно вставить в соответствующие ячейки, как показано на рис. 8-33.
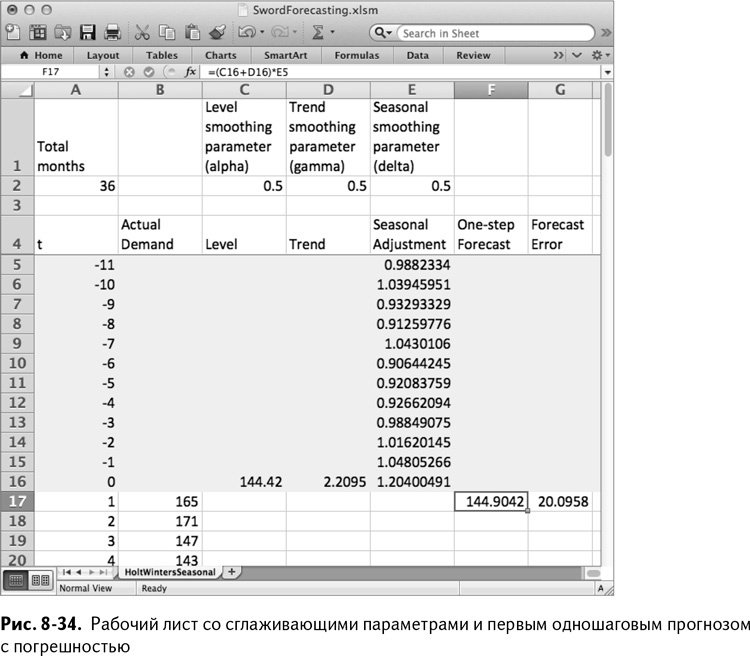
В столбце F вы делаете одношаговый прогноз. Для периода 1 он равен предыдущему уровню в С16, сложенному с предыдущим трендом в D16. Но они оба скорректированы соответствующими приближениями сезонности 12-ю строками выше в Е5. Таким образом, в F17 записано следующее:
=(C16+D16)*E5
Погрешность прогноза в G17 может быть рассчитана как
=B17-F17
Теперь вы готовы рассчитывать уровень, тренд и сезонность, шагая вперед. Таким образом в ячейках С2:Е2 располагаются значения альфа, гамма и дельта (как обычно, я начну с 0,5). Эта таблица показана на рис. 8-34.
Первое, что вы будете рассчитывать, двигаясь вперед во времени, – это новое приближение уровня для текущего периода: для периода 1 в ячейке С17 расчет будет таким:
=C16+D16+C$2*G17/E5
Как вы узнали из предыдущего раздела, новый уровень равен предыдущему, сложенному с предыдущим трендом и альфой, умноженным на десезонированную погрешность прогноза. Обновленный тренд в D17 рассчитывается практически так же:
=D16+D$2*C$2*G17/E5
Он, по сути, представляет собой предыдущий тренд плюс гамма, умноженные на величину десезонированной погрешности, встроенной в обновление уровня.
Обновленный сезонный фактор для января будет выглядеть следующим образом:
=E5+E$2*(1-C$2)*G17/(C16+D16)
Это фактор предыдущего января, скорректированный дельтой, умноженный на погрешность, проигнорированную при коррекции уровня, нормированный подобно сезонным факторам – с помощью последовательного деления на предыдущий уровень и тренд.
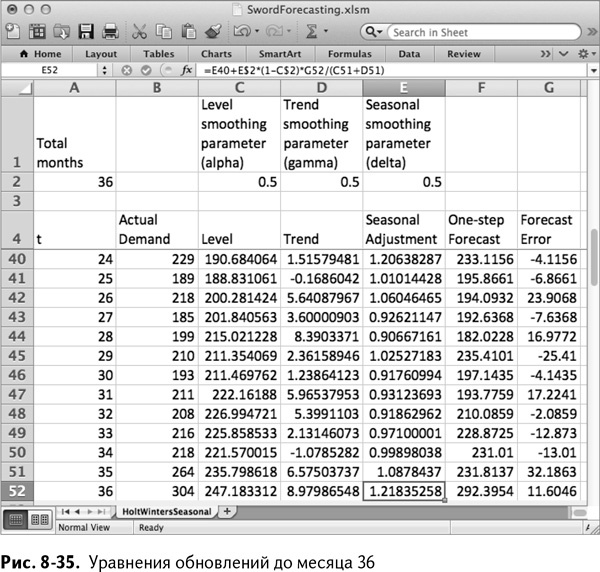
Обратите внимание, что все три формулы – альфа, гамма и дельта – имеют абсолютные ссылки, так что при перемещении расчета ничего не изменится. Растягивая С17:G17 вниз до месяца 36, получаем таблицу, изображенную на рис. 8-35.
Теперь, когда у вас есть итоговый уровень, тренд и сезонные приближения, вы можете спрогнозировать спрос на следующий год. Начиная с месяца 37 в ячейке В53 получаем:
=(C$52+(A53-A$52)*D$52)*E41
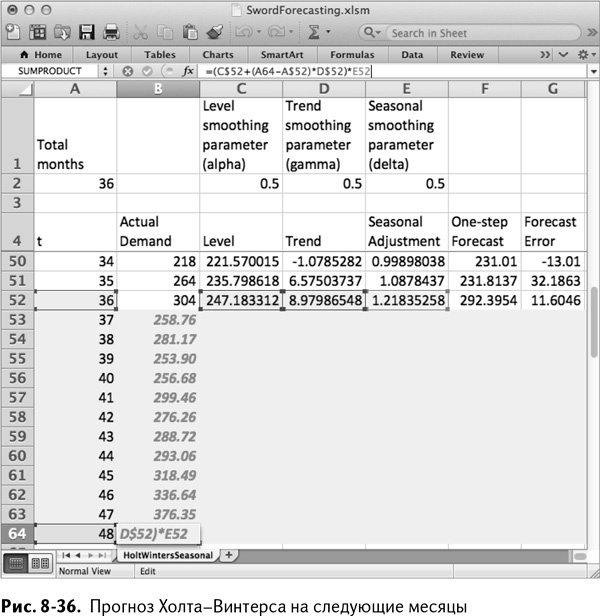
Как и в холтовском сглаживании с коррекцией тренда, берется последнее приближение уровня, к которому затем прибавляется тренд, умноженный на количество месяцев, прошедших с самого последнего приближения тренда. Единственная разница заключается в том, что весь прогноз нормируется по самому свежему сезонному множителю для января, который находится в ячейке Е41. А так как в уровне C$52 и тренде D$52 использованы абсолютные ссылки и они не изменяются при растягивании прогноза вниз, сезонная ссылка в Е41 должна двигаться вниз вместе с растягиванием прогноза на следующие 11 месяцев. Таким образом, растянув расчет вниз, вы получаете прогноз, показанный на рис. 8-36.
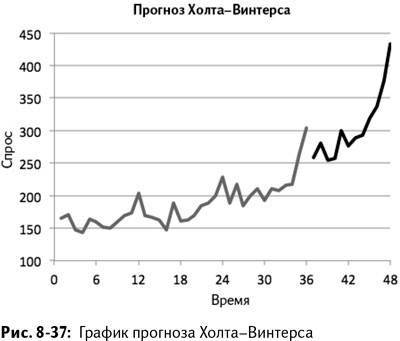
Вы можете создать график этого прогноза с помощью простой линейной диаграммы, как и в предыдущих двух методах (рис. 8-37).
И наконец… оптимизация!
Вы думали, что уже все сделали? Увы! Пора установить параметры сглаживания. Как и в предыдущих двух техниках, поместите сумму квадратов отклонений в ячейку G2, а стандартное отклонение – в Н2.
Операция отличается только тем, что параметров сглаживания три, поэтому стандартное отклонение рассчитывается как
=SQRT(G2/(36–3))
=КОРЕНЬ(G2/(36–3))
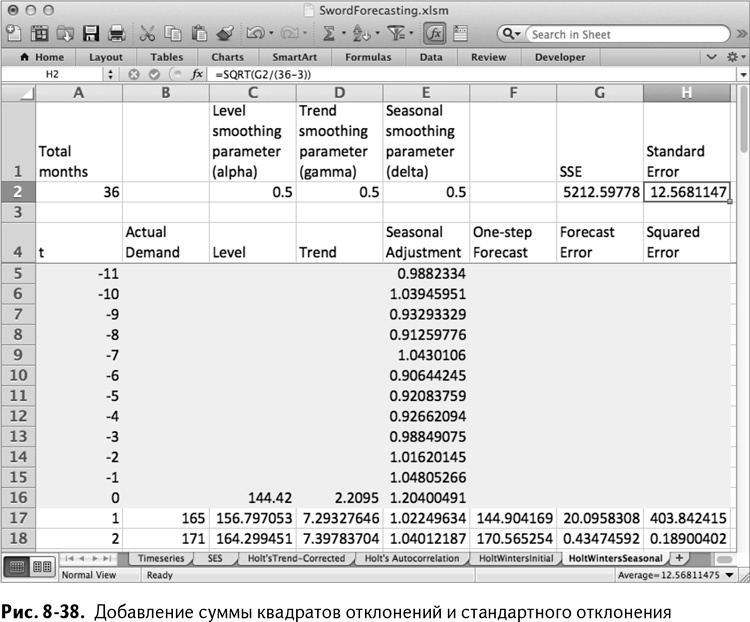
Так получается лист, изображенный на рис. 8-38.
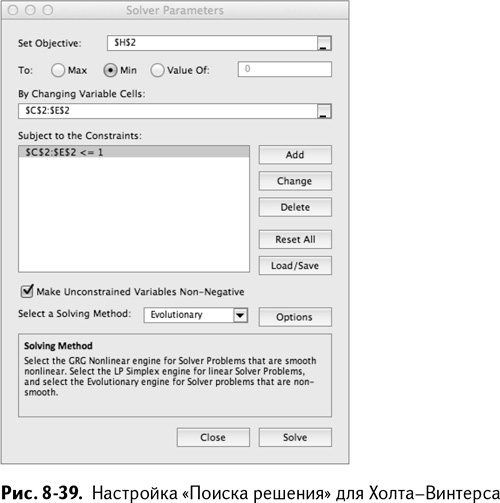
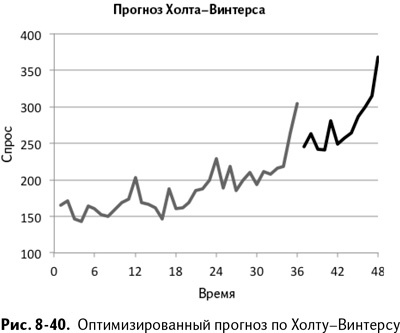
Что касается настройки «Поиска решения» (показанного на рис. 8-39), в этот раз мы оптимизируем Н2, варьируя три параметра сглаживания. Для вычисления стандартного отклонения подходит почти половина упомянутых техник. График прогноза (рис. 8-40) выглядит довольно симпатично, не правда ли? Вы следите за трендом и сезонными колебаниями.
Пожалуйста, скажите, что это все!!!
Теперь в сделанном прогнозе нужно проверить автокорреляции. Они у вас уже настроены – так что просто скопируйте их и вставьте новые значения погрешностей.
Создайте копию листа Holt Autocorrelation и назовите ее HW Autocorrelation. Затем вставьте специальной вставкой значения из столбца с погрешностями G в столбец В листа автокорреляции. Так получается коррелограмма, изображенная на рис. 8-41.
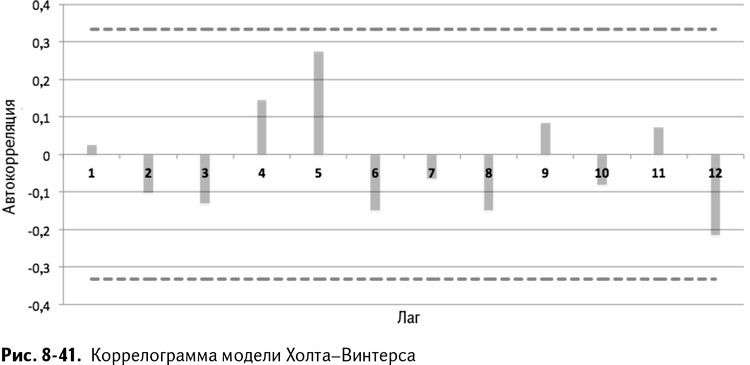
Бах! Так как выше критической точки 0,33 нет автокорреляций, вы понимаете, что модель неплохо поработала над пониманием структуры значений спроса.
Создаем интервал прогнозирования вокруг прогноза
Итак, у нас есть вполне рабочий прогноз. Как установить верхние и нижние границы, которые можно использовать для построения реалистичных предположений вместе с начальником?
В этом вам поможет симуляция Монте-Карло, с которой вы уже встречались в главе 4. Смысл заключается в том, чтобы сгенерировать будущие сценарии поведения спроса и определить группу, в которую попадают 95 % из них. С чего же начать? На самом деле процесс довольно прост.
Создайте копию листа HoltWintersSeasonal и назовите ее PredictionIntervals. Удалите оттуда все графики – они вам не нужны – и более того, сотрите прогноз из ячеек В53:В64. Вы запишете туда «реальный» (но симулированный) спрос.
Как я и предупреждал в начале главы, прогноз всегда неверен. В нем всегда есть отклонения. Но вы знаете, как они распределяются. У вас реалистичный прогноз, который, как вы предполагаете, имеет среднее одношаговое отклонение, равное 0 (непредвзято) со стандартным распределением, равным 10,37, как рассчитано в предыдущей вкладке.
Аналогично рассмотренному в главе 4, вы можете сгенерировать симуляцию отклонения с помощью функции NORMINV/НОРМОБР. Для будущих месяцев вам достаточно снабдить ее средним (0), стандартным распределением (10,37 в ячейке Н$2) и случайным числом от 0 до 1, а она выдаст отклонение из колоколообразной кривой. (Функция интегрального распределения рассматривается также в главе 4.)
Теперь поместим симуляцию одношаговой погрешности в ячейку G53:
=NORMINV(RAND(),0,H$2)
=НОРМОБР(СЛЧИС(),0,H$2)
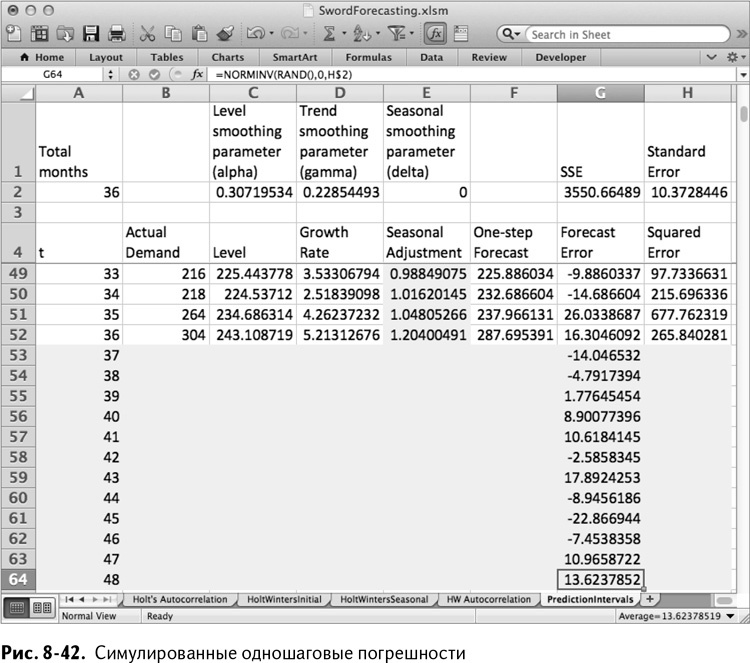
Растянув эту формулу вниз до G64, вы получите симуляции погрешностей для 12 месяцев одношагового прогноза. Так возникает лист, изображенный на рис. 8-42 (ваши значения симуляций будут отличаться от моих).
С погрешностью прогноза у вас есть все, что нужно для обновления приближений уровня, тренда и сезонности, которые следуют за одношаговым прогнозом. Так что выделите ячейки C52:F52 и растяните их до строки 64.
В результате у вас имеются симулированная погрешность прогноза и сам прогноз на шаг вперед. Вставив погрешность в столбец G а прогноз – в столбец F, можно фактически отказаться от симуляции спроса за этот период.
Таким образом, в В53 окажется просто:
=F53+G53
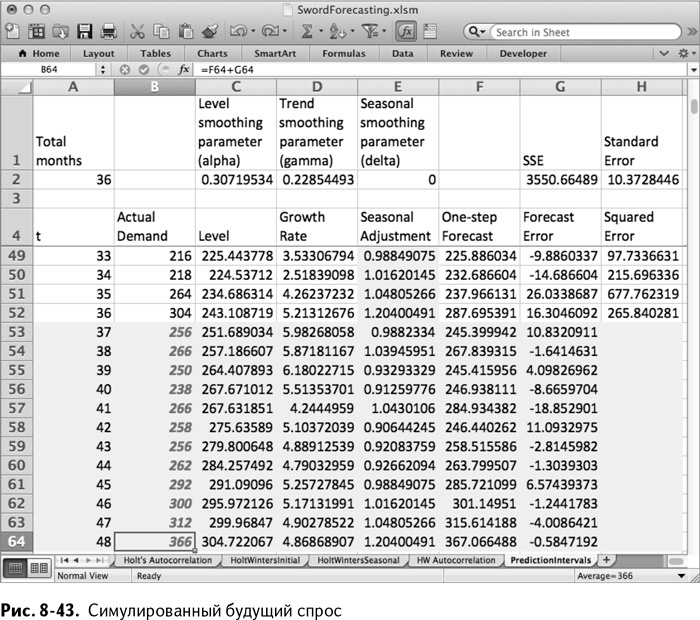
Растяните эту формулу до В64, чтобы получить величины спроса на все 12 месяцев (рис. 8-43).
Выполнив этот сценарий и обновив страницу, вы получаете новые значения спроса. Можно генерировать различные сценарии будущего спроса, просто копируя и вставляя один сценарий куда угодно, а затем наблюдая за меняющимися значениями.
Начните с называния ячейки А69 Simulated Demand, а ячеек А70:L70 – по месяцам, с 37 по 48. Это можно сделать простым копированием А53:А64 и специальной вставкой транспонированных значений в А70:L70.
Точно так же вставьте специальной вставкой транспонированные значения первого сценария спроса в А71:L71. Чтобы вставить второй сценарий, кликните правой клавишей мышки на строке 71 и выберите «Вставить» – так появится пустая строка 71. Теперь воспользуйтесь специальной вставкой и заполните ее другими симулированными значениями спроса (они должны были обновиться, когда вы вставляли предыдущую последовательность).
Можете продолжать выполнять эту операцию, пока у вас не будет столько сценариев будущего спроса, сколько вам хочется. Процесс, безусловно, утомляет? Тогда быстренько запишите макрос.
Как и в главе 7, проделайте следующие шаги:
• Вставка пустой строки 71.
• Копирование В53:В64.
• Специальная вставка транспонированных значений в строку 71.
• Нажатие кнопки остановки записи.
Записав эти нажатия клавиш, вы можете нажимать на ссылки макросов, которые вам нравятся (см. главу 7) снова и снова, пока у вас не окажется тонна сценариев. Можете даже подержать одну кнопку нажатой – такая тысяча сценариев вас тоже вполне устроит. (Если перспектива держания кнопки вам претит, погуглите и выясните, как зациклить код вашего макроса с помощью Visual Basic for Applicators.)
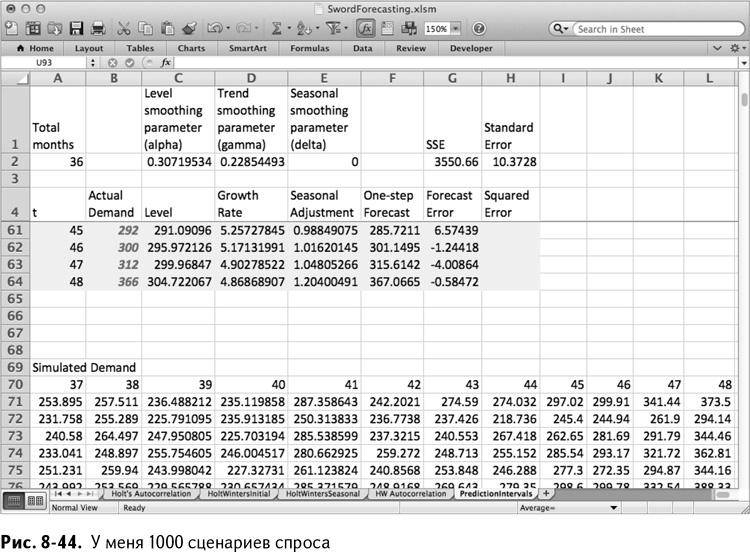
В завершенном виде ваша таблица должна быть похожей на рис. 8-44.
Теперь у вас есть сценарии на каждый месяц и вы можете использовать функцию PERCENTILE/ПЕРСЕНТИЛЬ, чтобы получить верхние и нижние границы в середине 95 % сценариев и создать интервал прогнозирования.
В качестве примера над месяцем 37 в А66 поместите формулу:
=PERCENTILE(A71:A1070,0.975)
=ПЕРСЕНТИЛЬ(A71:A1070,0.975)
Это даст вам 97,5-й персентиль спроса на данный месяц. В моей таблице он получается около 264. А в А67 можно получить 2,5-й персентиль:
=PERCENTILE(A71:A1070,0.025)
=ПЕРСЕНТИЛЬ(A71:A1070,0.025)
Обратите внимание: я использую интервал А71:А1070 из-за того, что у меня 1000 симулированных сценариев. Вы можете более или менее надеяться на проворство вашего указательного пальца. Если спросите меня, я скажу, что нижняя граница проходит примерно на 224.
Это значит, что, хотя прогноз на месяц 37 равен 245, 95 %-ный прогностический интервал – от 224 до 264.
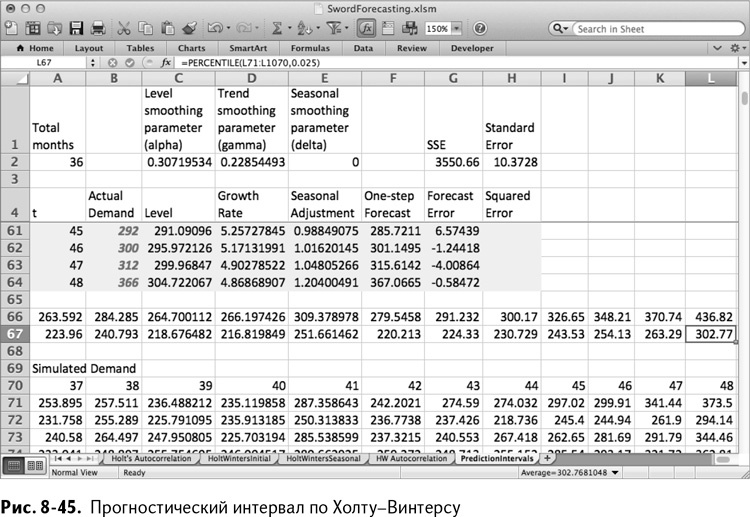
Растянув эти уравнения персентилей до месяца 48 в столбце L, вы получите полный интервал (рис. 8-45). Теперь есть что передать начальнику: скромный отчет и, если хотите, прогноз! Смело заменяйте 0,025 и 0,975 на 0,05 и 0,95 для 90 %-ного интервала или 0,1 и 0,9 для 80 %-ного, и т. д.
И диаграмма с областями для пущего эффекта
Этот последний шаг не обязателен, но обычно прогнозы с прогностическим интервалом изображаются в виде неких диаграмм с областями. Такую можно сделать и в Excel.
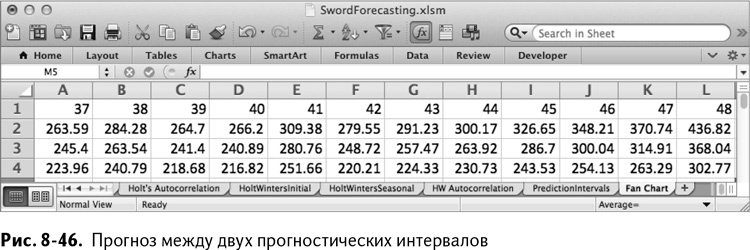
Создайте новый лист и назовите его Fan Chart. Вставьте в первую его строку месяцы с 37 по 48, а во вторую – значения верхней границы прогностического интервала из строки 66 вкладки PredictionsIntervals. В третью специальной вставкой поместите транспонированные значения текущего прогноза из вкладки HoltWintersSeasonal. В четвертую – значения нижней границы прогностического интервала из строки 67 таблицы с интервалами.
Итак, у нас есть месяцы, верхняя граница интервала, прогноз и нижняя граница интервала, все в ряд (рис. 8-46).
Выделив А2:L4 и выбрав «Диаграмму с областями» из меню диаграмм Excel, вы получаете три сплошные области, лежащие на графике друг над другом. Кликните правой кнопкой мыши на одной из последовательностей и нажмите «Выбрать данные». Измените название оси Х на одно из серии А1:L1, чтобы на графике отображались правильные месяцы.
Теперь кликните правой кнопкой мыши на серию нижних границ и отформатируйте их, чтобы цвет ячеек был белым. Уберите линии разметки графика, целостности ради. Не стесняйтесь добавлять названия осей и подписи. Так получается диаграмма с областями, изображенная на рис. 8-47.
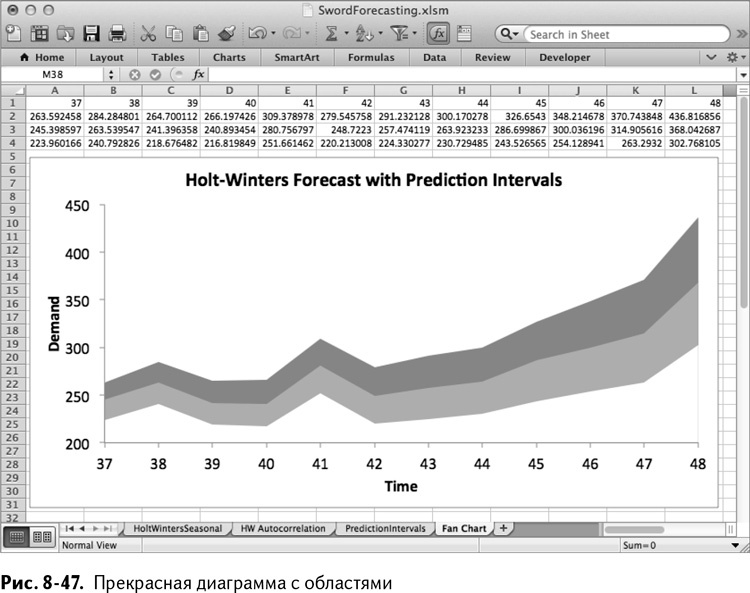
Самое замечательное в этой диаграмме то, что она передает и прогноз, и интервалы на одной простой картинке. Эх, можно было наложить и 80 %-ный интервал, было бы больше оттенков серого! На графике есть два интересных момента:
• Погрешность со временем становится шире. В этом есть смысл. Неуверенность накапливается с каждым месяцем.
• Точно так же погрешность растет и в частях, приходящихся на периоды сезонного повышения спроса. С последующим его падением погрешность сжимается.

