Книга: Много цифр. Анализ больших данных при помощи Excel
Назад: Бэггинг: перемешать, обучить, повторить
Дальше: Бустинг: если сразу не получилось, бустингуйте и пробуйте снова
Нужно еще сильнее!
Одноуровневого дерева решений недостаточно. Представьте, что у вас огромное количество деревьев, каждое из которых обучено на разной части данных и загрязненность результатов каждого – меньше 50 %? В таком случае стоит разрешить им голосование. Основываясь на проценте деревьев, проголосовавших за беременность, вы можете принять решение отнести покупателя к беременным.
Но вам нужно еще больше деревьев!
Одно вы уже обучили на столбце с фолиевой кислотой. Почему бы не сделать то же самое со всеми остальными столбцами?
У вас всего 19 признаков, и, честно говоря, некоторые из них, такие как адрес в виде дома или квартиры, несколько озадачивают. Так что вы имеете дело с 19 одноуровневыми деревьями сомнительного качества.
Но с помощью метода случайных подвыборок (бэггинга, bagging) можно «изготовить» сколько хотите деревьев. Бэггинг действует примерно таким образом:
1. Для начала откусывает кусочек выборки. Стандартная практика – взять приблизительный квадратный корень из количества признаков (четыре случайных столбца в нашем примере) и случайным образом две трети строк.
2. Строит дерево решений для каждого из этих четырех выбранных вами признаков, с помощью случайно выбранных 2/3 данных.
3. Из этих четырех деревьев выбирает чистейшее. Сохраняет. Перемешивает все заново в большом котле и обучает новое дерево.
4. Когда у вас накопится куча деревьев, соберите их вместе, заставьте проголосовать и назовите их единой моделью.
Обучим же ее!
Из обучающих данных вам нужно взять случайный набор строк и столбцов. Простейший способ это сделать – перемешать столбцы как колоду карт, а затем выбрать необходимое из верхнего левого угла таблицы.
Для начала скопируйте А2:U1002 из вкладки TD в верхнюю часть новой таблицы под названием TD_BAG (названия признаков вам не понадобятся – нужны только их порядковые номера из строки 2). Самый простой способ перемешать TD_BAG – это добавить еще один столбец и одну строку, заполненные случайными числами (с помощью оператора RAND/СЛЧИС). Сортировка по случайным значениям слева направо и сверху вниз, а затем выбор нужного количества из верхнего левого угла таблицы дает вам случайный набор строк и признаков.
Получение случайного образца
Вставьте пустую строку над номерами признаков и добавьте RAND/СЛЧИС в строку 1 (А1:S1) и в столбец V (V3:V1002). Таблица, получившаяся в результате, показана на рис. 7–4. Обратите внимание, что столбец V я назвал Random.
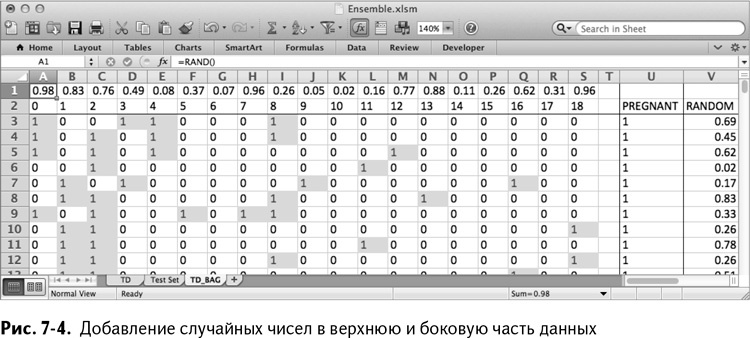
Отсортируйте столбцы и строки случайным образом. Начните со столбцов, так как поперечная сортировка предпочтительнее. Чтобы перемешать столбцы, выделите их от А до S кроме столбца Pregnant, который является не признаком, а зависимой переменной.
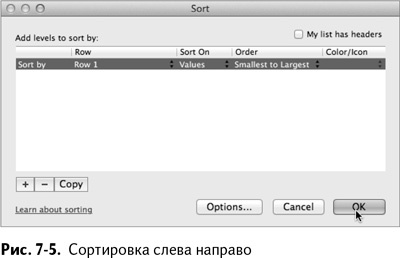
Откройте окно настраиваемой сортировки (более подробно она описана в главе 1). В окошке «Сортировка» (рис. 7–5) нажмите «Параметры» и выберите сортировку слева направо, чтобы ранжировать столбцы. Проверьте, что она проводится по строке 1, заполненной случайными числами. Также убедитесь, что напротив опции «Сортировать по существующему списку» не стоит галочка, так как у вас нет заголовков в горизонтальном направлении.
Нажмите ОК. Вы увидите, как столбцы в таблице перемешиваются.
Теперь то же самое нужно сделать со строками. В этот раз выберите промежуток А2:V1002, включая столбец Preganant, таким образом оставляя его привязанным к данным, за исключением строки случайных чисел вверху таблицы.
Снова откройте окошко настраиваемой сортировки и под разделом «Параметры» на этот раз выберите «Отсортировать сверху вниз».
Убедитесь, что отмечена опция «Сортировать по существующему списку», а затем выберите из выпадающего списка столбец Random. Окошко сортировки должно выглядеть, как показано на рис. 7–6.
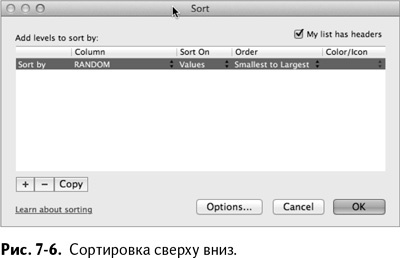
Теперь, когда вы рассортировали ваши данные случайным образом, выберите прямоугольник, образованный первыми четырьмя столбцами и первыми 666 строками. Создайте новый лист и назовите его RandomSelection. Чтобы выбрать случайный образец, укажите в ячейке А1 следующее:
=TD_BAG!A2
А затем скопируйте эту формулу до D667.
Вы можете получить значения Preganant рядом с образцом, направляя их прямо в столбец Е. Е1 указывает на ячейку U2 предыдущего листа:
=TD_BAG!U2
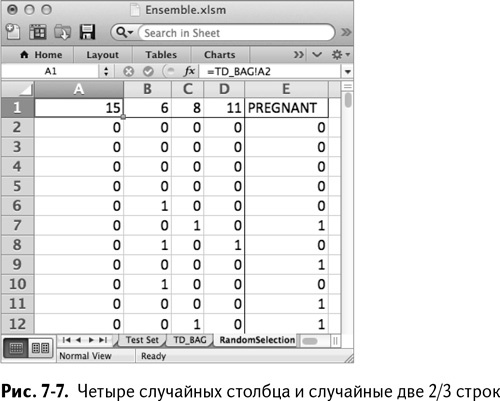
Кликните дважды на этой формуле, чтобы распространить ее на весь лист. Когда вы это сделаете, у вас не останется ничего, кроме случайных данных (рис. 7–7). Поскольку данные отсортированы случайным образом, в конце концов у вас остается четыре разных столбца с признаками.
Самое приятное то, что если вы вернетесь на лист TD_BAG и отсортируете все заново, этот образец обновится автоматически!
Выращиваем одноуровневое дерево из образца
Глядя на любой из этих четырех признаков, можно понять: есть только четыре вещи, которые могут произойти между одним признаком и зависимой переменной Preganant:
• признак может иметь значение 0, а Preganant – 1;
• признак может иметь значение 0, а Preganant – 0;
• признак может иметь значение 1, а Preganant – 1;
• признак может иметь значение 1, а Preganant – 0.
Вам нужно сосчитать количество обучающих строк, попадающих в каждый из этих случаев, чтобы построить дерево по признаку, аналогичное тому, что изображено на рис. 7–2. Для этого пронумеруйте четыре обозначенные комбинации нулей и единиц в G2:H5. Настройте I1:L1 так, чтобы в нем были порядковые номера из А1:D1.
Теперь таблица выглядит, как на рис. 7–8.
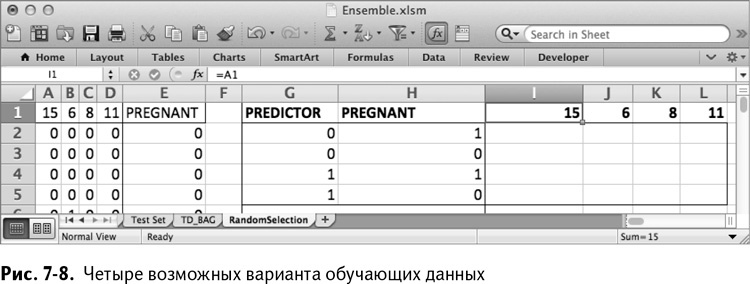
После настройки этой небольшой таблицы вам нужно заполнить ее количествами обучающих строк, значения которых совпадают с комбинацией прогноза и значением в столбце Preganant. Для верхнего левого угла таблицы (первый признак в моем случайном наборе оказался с номером 15) вы можете сосчитать количество обучающих строк, в которых признак 15 имеет значение 0, а столбец Preganant – значение 1, с помощью следующей формулы:
=COUNTIFS(A$2:A$667,$G2,$E$2:$E$667,$H2)
=СЧЁТЕСЛИМН(A$2:A$667,$G2,$E$2:$E$667,$H2)
Формула COUNTIFS/СЧЁТЕСЛИМН позволяет вам сосчитать строки, удовлетворяющие нескольким критериям (спасибо S//МН в конце названия!). Первый критерий смотрит на промежуток признака номер 15 (А2:А667) и проверяет его на строки, идентичные значению ячейки G2 (0), в то время как второй критерий проверяет отрезок Preganant (Е2:Е667) на строки, идентичные значению ячейки Н2 (1).
Скопируйте эту формулу во все остальные ячейки таблицы, чтобы получить количества для каждого случая (рис. 7–9).
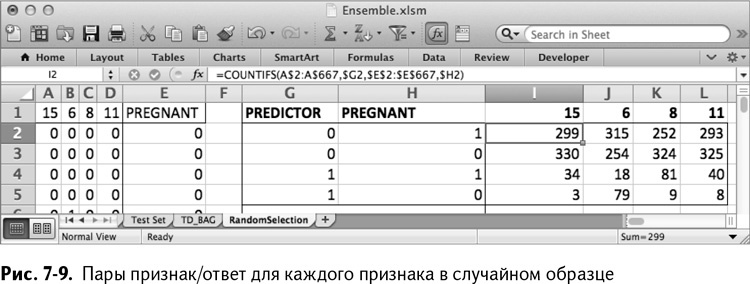
Если бы каждый из этих признаков был деревом решений, то какое значение признака являлось бы индикатором беременности? Несомненно, значение с самой высокой концентрацией беременных покупателей в образце.
В строке 6 под значениями количества вы можете сравнить эти отношения. Поместите в I1 формулу:
=IF(I2/(I2+I3)>I4/(I4+I5),0,1)
=ЕСЛИ(I2/(I2+I3)>I4/(I4+I5),0,1)
Если отношение беременных покупателей, ассоциированное с нулевым значением признака (I2/(I2+I3)), больше, чем ассоциированное с единицей (I4/(I4+I5)), то 0 – показатель беременности в этом дереве. Если все наоборот, то 1. Скопируйте эту формулу вправо до столбца L. Таким образом получится лист, изображенный на рис. 7-10.
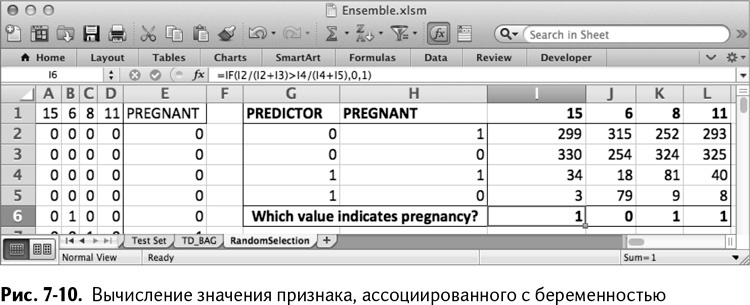
Используя значения в строках с 2 по 5, вы можете рассчитать значения загрязненности для групп каждого дерева решений, которое вы выбрали для разделения по признаку.
Вставим расчет загрязненности в строку 8 под подсчетом случаев. Так же, как и на рис. 7–3, вам нужно вычислить значение загрязненности для обучающих случаев, имеющих значение признака 0, и усреднить их с теми, у которых 1.
Если вы используете первый признак (номер 15 для меня), 299 беременных и 330 «не-беременных» оказались в группе 0, так что загрязненность равна 100 % – (299/629)^2 – (330/629)^2, что можно ввести в таблицу следующим образом:
=1–(I2/(I2+I3))^2-(I3/(I2+I3))^2
Точно так же загрязненность для группы 1 может быть записана так:
=1-(I4/(I4+I5))^2-(I5/(I4+I5))^2
Вместе они составляют взвешенное среднее: каждая загрязненность умножается на количество обучающих случаев в группе, затем результаты складываются и делятся на общее количество случаев, то есть 666:
=(I8*(I2+I3)+I9*(I4+I5))/666
Теперь вы можете растянуть этот расчет загрязненности на все признаки, получая комбинированные значения для каждого из возможных деревьев решений, как показано на рис. 7-11.
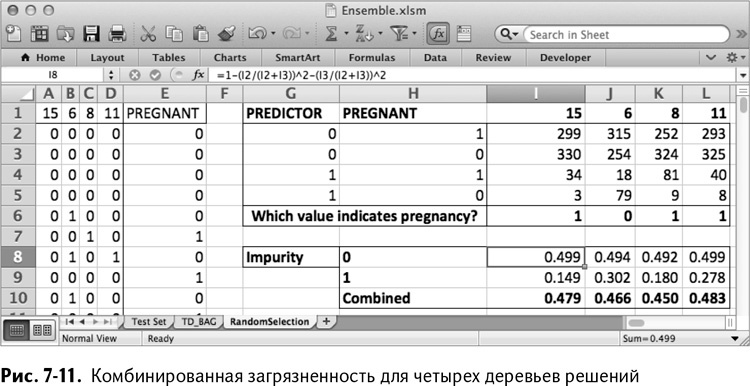
Ваши значения загрязненностей наверняка будут отличаться от моих – ведь мы пользовались генератором случайных чисел. В моем случае победителем явно является номер 8 (заглянув в лист TD, можно найти название признака, это – витамины для беременных) со значением 0,450.
Записываем победителя
Итак, витамины в моем варианте победили. У вас результат наверняка оказался другим, и теперь следует его где-то записать.
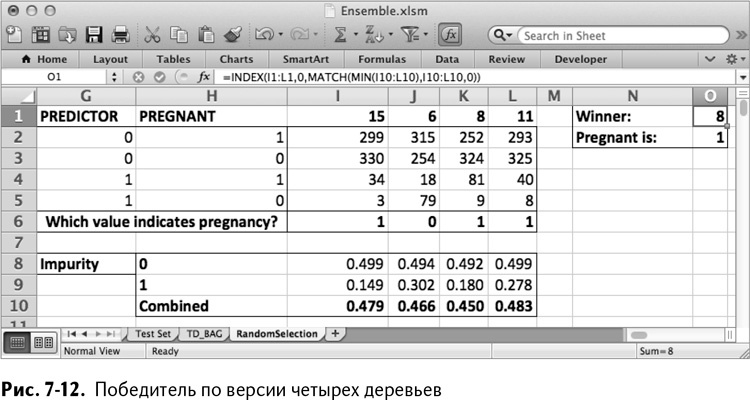
Назовите ячейки N1 и N2 Winner и Pregnant Is. Вы сохраняете выигравшие деревья в столбце О. Начните с сохранения номера выигравшего столбца в ячейке О1. Это будет значение из промежутка I1:L1 с минимальной загрязненностью (в моем случае это 8). Вы также можете скомбинировать формулы MATCH/ПОИСКПОЗ и INDEX/ИНДЕКС, чтобы они нашли его за вас (более подробно о них рассказано в главе 1):
=INDEX(I1:L1,0,MATCH(MIN(I10:L10),I10:L10,0))
=ИНДЕКС(I1:L1,0,ПОИСКПОЗ(МИН(I10:L10),I10:L10,0))
MATCH(MIN(I10:L10),I10:L10,0))/ПОИСКПОЗ(МИН(I10:L10),I10:L10,0)) находит столбец с минимальной загрязненностью в строке 10 и передает информацию функции INDEX/ИНДЕКС. Эта функция определяет положение названия соответствующего признака.
Аналогично в О2 можно определить, 0 или 1 ассоциируется с беременностью – найти значение в строке 6 в столбце с минимальной загрязненностью:
=INDEX(I6:L6,0,MATCH(MIN(I10:L10),I10:L10,0))
=ИНДЕКС(I6:L6,0,ПОИСКПОЗ(МИН(I10:L10),I10:L10,0))
Выигравшее дерево решений и его ассоциированная с беременностью группа затем выписываются, как показано на рис. 7-12.
Встряхни меня, Джуди!
Фух! Я знаю, что это была целая куча маленьких шажков и всего одно дерево. Но сейчас, когда все формулы уже на месте, следующая пара сотен будет сущим пустяком.
Второе дерево можно сделать очень быстро. Перед этим не забудьте сохранить только что построенное! Для этого просто скопируйте и вставьте значения из О1:О2 в Р1:Р2.
Чтобы создать новое дерево, переключитесь на лист TD_BAG и снова перемешайте столбцы и строки.
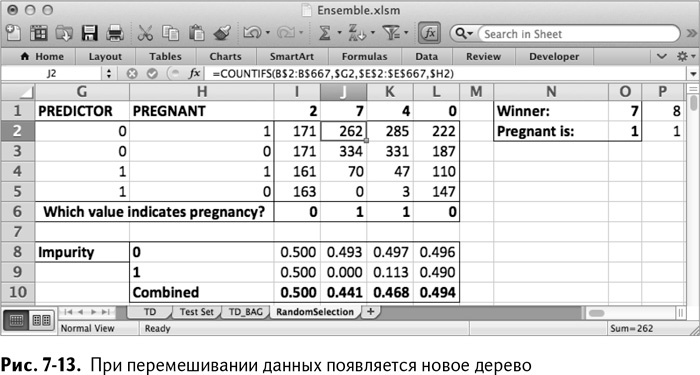
Вернитесь на лист RandomSelection. Вуаля! Победитель изменился. В моем случае это фолиевая кислота, и значение, соответствующее беременности, – 1 (рис. 7-13). Предыдущее дерево сохранилось справа.
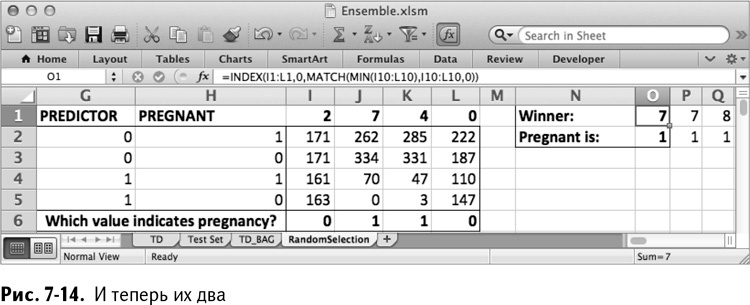
Чтобы сохранить второе дерево, кликните правой кнопкой на столбец Р и выберите «Вставить», чтобы сместить первое дерево вправо. Ансамбль теперь выглядит так, как показано на рис. 7-14.
Как видите, с этим вторым дело пошло гораздо быстрее, чем с первым. Так что продолжайте…
Скажем, вы хотите ансамбль из 200 моделей. Все, что вам нужно сделать, – это повторить эти шаги еще 198 раз. Ничего невозможного, просто надоедает.
Почему бы вам просто не записать это действие в макрос и затем проигрывать его? Оказывается, перемешивание очень подходит для макроса.
Для тех, кто никогда не записывал макрос: это не что иное, как запись серии повторяющихся нажатий на клавиши, чтобы потом можно было ее проиграть вместо того, чтобы самому зарабатывать туннельный синдром.
Так что ищем на панели меню Вид → Макрос (в MacOs Инструменты → Макрос) и выбираем «Начать запись».
Нажатие кнопки «Запись» откроет окно, в котором вы сможете дать своему макросу название, например GetBaggedStump. Удобства ради проассоциируем вызов макроса с комбинацией клавиш. У меня MacOS, так что все мои комбинации начинаются с Option + Cmd, к которым я хочу добавить Z, потому что сегодня у меня такое настроение (рис. 7-15).
Нажмите ОК, чтобы начать запись. Вот шаги, которые нужны для создания одноуровневого дерева решений:
1. Нажать на лист TD_BAG.
2. Выделить столбцы от А до S.
3. Вручную рассортировать столбцы.
4. Выделить строки от 2 до 1002.
5. Вручную рассортировать строки.
6. Переключиться на лист RandomSelection.
7. Кликнуть правой клавишей мышки на столбце Р и вставить новый пустой столбец.
8. Выделить и скопировать выигрышное дерево из О1:О2.
9. Вставить «Специальной вставкой» значения в Р1:Р2.
Перейдите в меню Вид → Остановить запись (Инструменты → Остановить запись в Excel 2011 для MacOs), чтобы закончить запись.
Теперь вы можете создавать новые деревья решений простым нажатием комбинации клавиш, активирующей макрос. Подождите, пока я понажимаю на клавиши раз так 19 800…
Оценка бэггинговой модели
Вот это бэггинг! Все, что нужно сделать – это перемешать данные, взять подвыборку, обучить простой классификатор – и все по новой! Накопив в своем ансамбле пачку классификаторов, вы будете готовы делать прогнозы.
Когда вы запустите макрос дерева решения пару сотен раз, лист RandomSelection будет выглядеть примерно так, как показано на рис. 7-16 (ваши деревья могут отличаться от моих).
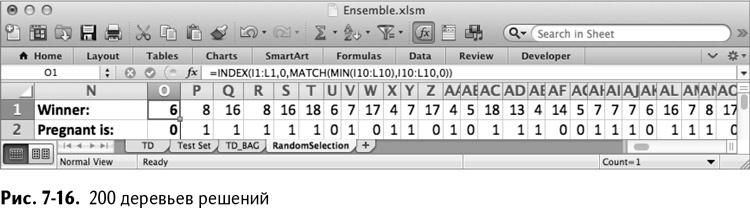
Прогнозирование на тестовой выборке
Теперь, когда у вас есть деревья, пришло время опробовать модель на тестовых данных. Создайте копию листа TestSet и назовите ее TestBag.
Переместитесь на лист TestBag и вставьте две пустые строчки в самый верх листа – это будет место для новых деревьев.
Вставьте значения деревьев из листа RandomSelection (Р1:HG2, если у вас их 200) в лист TestBag, начиная со столбца W. Таким образом получается лист, изображенный на рис. 7-17.
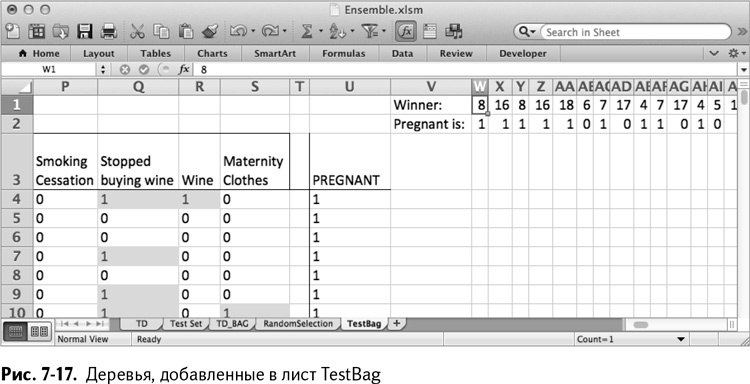
Вы можете запускать по одной строке тестовых данных в каждое дерево. Начните с первой строки данных (строка 4) и первого дерева в столбце W. Можете использовать формулу OFFSET/СМЕЩ, чтобы найти значение из столбца с деревом, записанное в W1. Если это значение равняется значению в W2, то дерево прогнозирует беременность покупателя. В противном случае прогноз дерева – покупатель не является беременным. Формула выглядит так:
=IF(OFFSET($A4,0,W$1)=W$2,1,0)
=IF(СМЕЩ($A4,0,W$1)=W$2,1,0)
Ее можно скопировать во все деревья на всем листе (обратите внимание на абсолютные ссылки). Таким образом получается лист, изображенный на рис. 7-18.
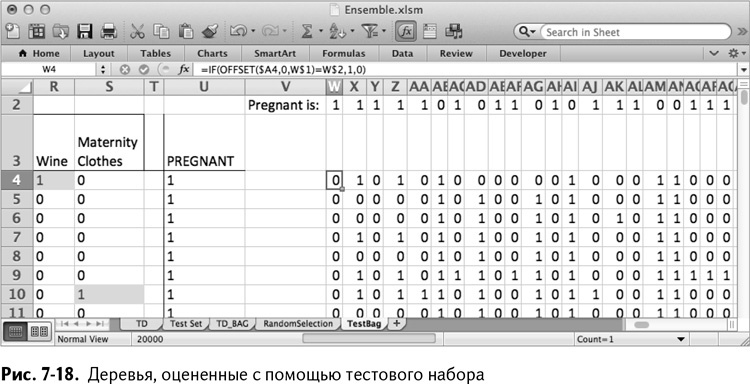
В столбце V вычислите среднее значение строк слева, чтобы получить классовую вероятность для беременности. К примеру, для V4, если у вас 200 деревьев, формула будет такова:
=AVERAGE(W4:HN4)
=СРЗНАЧ(W4:HN4)
Скопируйте ее на весь столбец V, чтобы получить прогнозы для каждого столбца тестового набора, как показано на рис. 7-19.
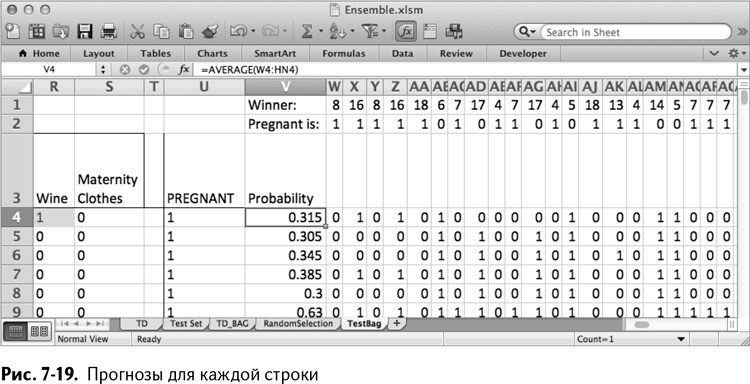
Качество работы
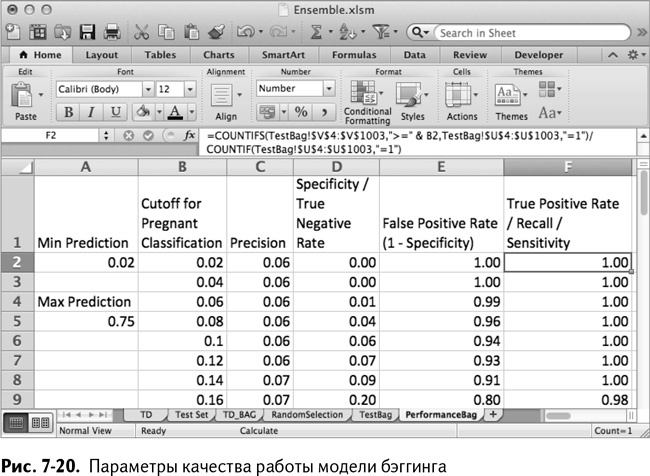
Вы можете оценить эти прогнозы, используя те же параметры оценки работы и расчеты, что и в главе 6. Сначала создайте новый лист под названием PerformanceBag. В первом столбце найдите максимальный и минимальный прогнозы. Для моих 200 деревьев эти значения получились равными 0,02 и 0,75.
Поместите в столбец В серию граничных значений от минимума до максимума (в своем случае я сделал шаг равным 0,02). Точность, специфичность, доля положительных результатов и чувствительность вычисляются так же, как и в главе 6.
Таким образом получается лист, изображенный на рис. 7-20.
Обратите внимание на граничное значение прогноза 0,5 – при половине деревьев, проголосовавших за беременность, вы можете идентифицировать 33 беременных покупателя с одним лишь процентом ложноположительных результатов (напоминаю, что в вашем варианте это может быть совсем другое граничное значение – ведь мы используем случайные числа). Весьма неплохо для нескольких простых деревьев!
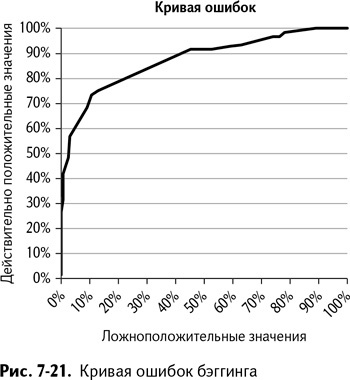
Также вы можете вставить кривую ошибок, пользуясь долей ложноположительных и ложноотрицательных результатов (столбцы Е и F), опять же как в главе 6. График для моих 200 деревьев изображен на рис. 7-21.
Еще кое-что о работе модели
Так как бэггинговая модель с одноуровневыми деревьями поддерживается промышленными пакетами программ, такими, к примеру, как пакет randomForest для R, я хотел бы особо выделить два отличия между этой и типовыми моделями.
• Обычные случайные леса выбирают образцы с заменой, в том смысле, что одна и та же строка обучающих данных может быть отобрана в образцы больше одного раза. Вы можете выбрать то же количество записей, что и в вашем обучающем наборе, не ограничиваясь двумя третями. У выбора с заменой выше статистические характеристики, но если вы работаете с достаточно большим объемом данных, то особой разницы между этими двумя методами нет.
• Случайные леса по умолчанию выращены из деревьев полной классификации, а не из одноуровневых. Полное дерево таково, что, разделив данные на два класса, вы выбираете все новые признаки для деления, пока, наконец, не столкнетесь с ограничительным критерием. Деревья полной классификации лучше, чем одноуровневые, если между признаками есть какая-либо связь, которую можно смоделировать.
Переходя к точности модели, привожу несколько преимуществ бэггингового подхода:
• бэггинг устойчив к выбросам и не пытается слишком сильно подгонять данные. Слишком сильная подгонка приводит к тому, что модель отражает не только ваши данные, но и статистический шум;
• процесс обучения можно проводить параллельно, потому что обучение одного слабообучаемого не зависит от обучения предыдущего слабообучаемого;
• этот тип модели способен обрабатывать тонны переменных решения.
Модели, используемые нами в MailChimp.com для предсказания спама и домогательств, – это модели случайного леса, которые мы обучаем параллельно с помощью примерно 10 миллиардов строк необработанных данных. Такое нельзя проделать в Excel, и я абсолютно уверен, что не стал бы пользоваться для этого макросом.
Я использую язык программирования R с пакетом randomForest, о котором я рекомендую узнать поподробнее, если вы собираетесь использовать какую-нибудь из этих моделей в своей организации. С помощью randomForest можно построить и модель, рассматриваемую в этой главе, – надо всего лишь отключить выбор с заменой и установить максимальное количество групп в деревьях принятия решений на 2 (подробнее в главе 10).
Назад: Бэггинг: перемешать, обучить, повторить
Дальше: Бустинг: если сразу не получилось, бустингуйте и пробуйте снова

