Бэггинг: перемешать, обучить, повторить

Книга: Много цифр. Анализ больших данных при помощи Excel

Бэггинг (метод случайных подвыборок) – это техника, которая используется для обучения нескольких классификаторов (ансамбля, с вашего позволения), но не на абсолютно одинаковых выборках. Дело в том, что если вы будете обучать классификаторы на одинаковых данных, они сами станут одинаковыми – но вам же нужно разнообразие моделей, а не пачка копий одной и той же модели! Бэггинг позволяет внести в набор классификаторов небольшое разнообразие.

Одноуровневое дерево решений – неудачное название «неумного» определителя

В строящейся нами модели бэггинга отдельные классификаторы будут одноуровневыми деревьями решений. Одноуровневое дерево решений – не более чем один вопрос, который вы обращаете к данным. В зависимости от ответа вы можете понять, ожидает ли семья ребенка или нет. Простые классификаторы вроде этого часто называют weak learner – слабообучаемыми.

К примеру, если в обучающих данных вы сосчитаете, сколько раз «беременная» семья заказывала препараты фолиевой кислоты, выделив Н3:Н502, и сложите результаты в итоговой строке, то узнаете, что 104 «беременные» семьи сделали такой заказ до рождения ребенка. С другой стороны, только двое «не-беременных» покупателей заказали фолиевую кислоту.

Так что между заказом препаратов фолиевой кислоты и беременностью, бесспорно, существует связь. Можно использовать эту простую зависимость для сборки такого слабообучаемого классификатора:

Покупали ли семьи фолиевую кислоту? Если да, то считать их «беременными». Если нет, то считать их «не-беременными».

Такой прогностический классификатор изображен на рис. 7–2.

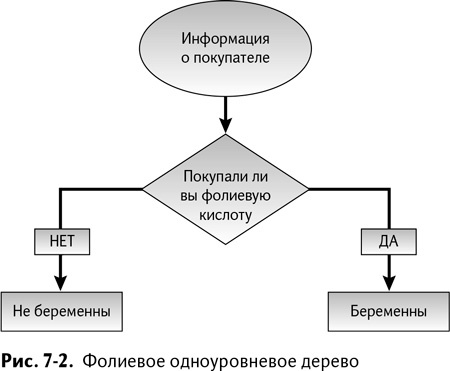
А мне не кажется, что это глупо!

Дерево решений на рис. 7–2 делит выборку обучающих записей на две подвыборки. Вы, наверное, думаете, что это дерево имеет глубокий смысл? Что ж, в известной степени вы правы. Хотя смысл этот все-таки не настолько глубок, как вам кажется. В конце концов, в вашей обучающей выборке имеется около 400 «беременных» семей, которые не покупали фолиевую кислоту и были неправильно классифицированы деревом решений.

Все равно лучше, чем вовсе никакой модели, да?

Несомненно. Но вопрос в том, насколько данное дерево лучше полного отсутствия модели. Один из способов оценить это – применить параметр под названием node impurity – загрязненность класса.

Этим способом измеряется, как часто выбранная запись покупателя была неправильно классифицирована в качестве беременной или «не-беременной», если классификация производилась случайным образом, согласно распределению покупателей в своей подвыборке дерева решений.

К примеру, можно начать с отнесения всей тысячи покупателей в одну подвыборку, что является, скажем прямо, стартом без модели.

Вероятность того, что вы выберете беременного покупателя из кучи, равна 50 %. Классифицировав его случайным образом, исходя из соотношения 50/50, вы получите 50 %-ный шанс правильно угадать класс.

Таким образом, получается 50 % × 50 % = 25 % вероятность выбора беременного покупателя и правильного угадывания факта беременности. Аналогично равна 25 % вероятность выбора «не-беременного» покупателя и угадывания того, что он не является беременным. Все, что не относится к этим двум случаям – просто версии неверных догадок.

Значит, у нас есть 100 % – 25 % – 25 % = 50 % шанс неправильного отнесения покупателя к классу.

Дерево решений по фолиевой кислоте делит этот набор из 1000 записей на две группы – 894 человека, не купивших фолиевые препараты, и 106 купивших. У каждой из этих подвыборок своя собственная загрязненность, так что, усреднив загрязненность обеих подвыборок (принимая во внимание разницу в их размере), вы сможете узнать, насколько одноуровневое дерево исправило ситуацию.

Из 894 покупателей, попавших в «не-беременную» корзину, 44 % беременны, а 56 % – нет. Загрязненность можно рассчитать как 100 % – 44 %^2–56 %^2 = 49 %. Не такое уж большое улучшение.

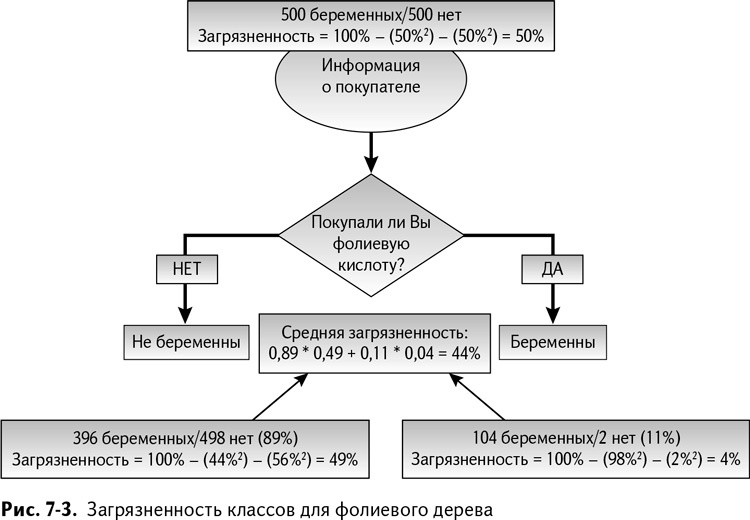
Что касается тех 106 покупателей, которых мы поместили в «беременную» категорию: 98 % из них беременны, и только 2 % – нет. Загрязненность будет равна 100 % – 98^2–2^2 = 4 %. Усреднив общее значение загрязненности, получаем 44 %. Это получше, чем бросать монетку!

Расчет загрязненности показан на рис. 7–3.

Делим свойство на большее количество частей

В примере РитейлМарта все независимые переменные бинарны. Вам не нужно думать, как разделить обучающие данные для дерева принятия решений – единицы отправляются в одну сторону, нули – в другую. Но что, если у вас есть признак, имеющий все варианты значения?

К примеру, один из прогнозов, который мы делаем в MailChimp.com, – это жив ли почтовый ящик и может ли он принимать почту. Один из используемых для этого параметров – количество дней, прошедших с момента отправления последнего письма на этот адрес. (Мы отправляем около 7 миллиардов писем в месяц, так что кое-какие данные у нас есть на каждого…)

Этот признак совершенно не бинарен! И если мы обучаем дерево решений, которое его использует, то как определить, на сколько частей его делить, чтобы направить одну часть данных в одном направлении, а другую – в другом?

На самом деле все очень просто.

Существует ограниченное число групп, на которые вы можете поделить дерево. Максимум – это одна запись из вашей последовательности в каждой группе. И наверняка в вашем наборе есть такие адреса, у которых количество дней будет точно таким же, как прошло с последнего вашего письма им.

Вам нужны только эти значения. Если у вас есть четыре уникальных значения, на которые вы можете поделить обучающую выборку (скажем, 10, 20, 30 и 40 дней), деление на 35 не сложнее деления на 30. Так что вы просто проверяете значения загрязненности для каждого выбранного вами деления, а затем выбираете количество групп с наименьшей загрязненностью. Готово!

Назад: Используем данные из главы 6

Дальше: Нужно еще сильнее!