Книга: Много цифр. Анализ больших данных при помощи Excel
Назад: Нужно еще сильнее!
Дальше: Подытожим
Бустинг: если сразу не получилось, бустингуйте и пробуйте снова
Давайте вспомним, зачем мы занимались бэггингом.
Если вы обучаете пачку деревьев поиска решений на полном наборе данных несколько раз, снова и снова, то они будут идентичны. Выбирая образцы из базы данных случайным образом, вы вносите немного разнообразия в ваши деревья и, в конце концов, находите такие нюансы в обучающих данных, которые одно дерево ни за что бы не обнаружило.
Бэггинг делает со случайным выбором то же самое, что бустинг делает с весами. Бустинг не выбирает случайные порции из набора данных – он использует весь набор данных в каждой итерации обучения. Он фокусируется на обучении дерева решений, которое исправляет некоторые грехи, совершенные предыдущими деревьями. Алгоритм таков:
• Сначала все строки обучающих данных считаются одинаковыми. Все они имеют одинаковый вес. В вашем случае есть 100 строк, и все они начинают с весом 0,001. То есть в сумме все веса составляют единицу.
• Оцените каждый признак на фоне остальных, чтобы выбрать лучшее дерево решений. Кроме того, если мы применяем бустинг, а не бэггинг, то победит дерево с минимальным взвешенным отклонением (погрешностью). Каждое ложное предположение для возможного дерева считается штрафом, равным весу строки. Сумма этих штрафов и есть взвешенная погрешность. Выберите дерево с минимальной взвешенной погрешностью.
• Веса регулируются. Если выбранное дерево решений правильно предсказывает строку, то ее вес уменьшается. Если выбранное дерево решений ошибается со строкой, то вес строки растет.
• Новые деревья обучаются с помощью этих новых весов. Таким образом, по ходу выполнения, алгоритм больше концентрируется на строках с обучающими данными, которые предыдущие деревья обработали плохо. Деревья обучаются, пока взвешенное отклонение не достигнет порога.
Что-то из этого может показаться немного непонятным, но процесс сделает все абсолютно ясным в таблице. Вперед, к данным!
Обучаем модель: каждому признаку – шанс
В бустинге каждый признак – это возможное дерево в каждой итерации. В этот раз вам не придется выбирать по четыре.
Для начала создайте лист под названием BoostStumps. Вставьте в него возможные комбинации признака/результата из промежутка G1:H5 листа RandomSelection.
Рядом с этими значениями в строку 1 вставьте номера признаков (0–18). В итоге получается лист, изображенный на рис. 7-22.
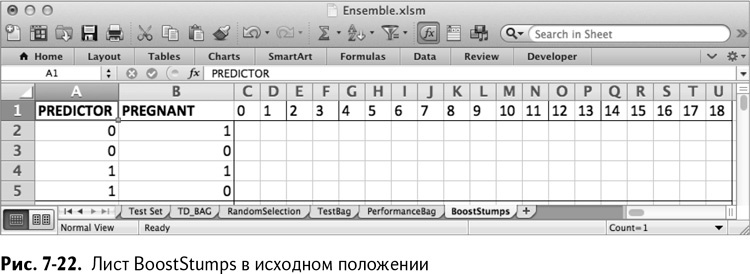
Под каждым номером, как и в бэггинге, нужно сложить количество строк обучающего набора, которые попадают в каждую из четырех комбинаций значения признака и независимой переменной, данных в столбцах А и В.
Начните в ячейке С2 (номер признака 0) со сложения количества обучающих строк, имеющих 0 в графе данного признака и являющихся беременными. Это можно вычислить с помощью формулы COUNTIFS/СЧЁТЕСЛИМН:
=COUNTIFS(TD!A$3:A$1002,$A2,TD!$U$3:$U$1002,$B2)
=СЧЁТЕСЛИМН(TD!A$3:A$1002,$A2,TD!$U$3:$U$1002,$B2)
Использование абсолютных ссылок позволяет вам раскопировать эту формулу до U5. Так получается лист, изображенный на рис. 7-23.
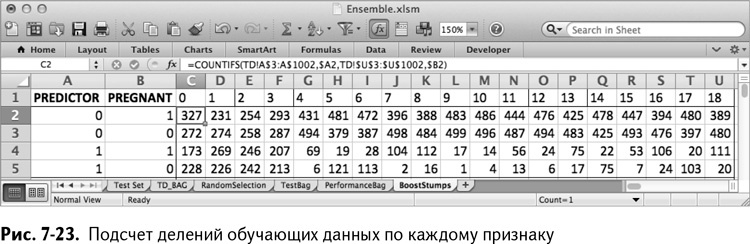
Так же, как и в бэггинге, в С6 вы можете найти значение, ассоциированное с беременностью для признака номер 0, глядя на соотношение беременных, ассоциированных со значениями признака, равными 0 и 1:
=IF(C2/(C2+C3)>C4/(C4+C5),0,1)
=ЕСЛИ(C2/(C2+C3)>C4/(C4+C5),0,1)
Эту формулу можно раскопировать до столбца U.
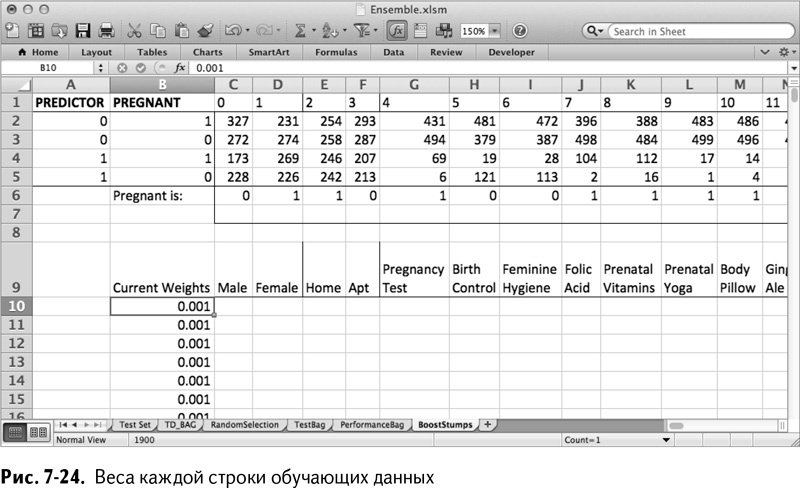
Теперь запишите в столбец В веса для каждого значения данных. Начните с В9 – назовите ячейку Current Weights, а под ней, до самой В1009, введите по 0,001 для каждой из тысячи обучающих строк. В строку 9 вставьте названия признаков из листа TD, чтобы было легче за ними следить.
Так получается лист, который показан на рис. 7-24.
Для каждого из этих возможных деревьев решений нужно вычислить взвешенную погрешность. Это делается путем определения положения обучающих строк, отнесенных к неправильному классу, и выписывания штрафа в размере их весов.
К примеру, в ячейке С10 можно оглянуться на данные из первой обучающей строки для признака номер 0 (А3 на листе TD). Если они совпадают с индикатором беременности в С6, то вы получаете штраф (вес в ячейке В10), если строка (конечно, имеется в виду покупатель из строки) «не-беременна». Если же значение признака не совпадает с С6, то вы получаете штраф в случае беременности покупателя в строке. Получается такая формула с двумя операторами IF/ЕСЛИ:
=IF(AND(TD!A3=C$6,TD!$U3=0),$B10,0)+
IF(AND(TD!A3<>C$6,TD!$U3=1),$B10,0)
=ЕСЛИ(И(TD!A3=C$6,TD!$U3=0),$B10,0)+
ЕСЛИ(И(TD!A3<>C$6,TD!$U3=1),$B10,0)
Абсолютные ссылки позволяют раскопировать формулу до U1009. Взвешенная погрешность для каждого возможного дерева решений затем может быть рассчитана в строке 7. Для ячейки С7 расчет взвешенной погрешности таков:
=SUM(C10:C1009)
=СУММА(C10:C1009)
Скопируйте это в строку 7, чтобы получить взвешенную погрешность для каждого дерева решений (рис. 7-25).
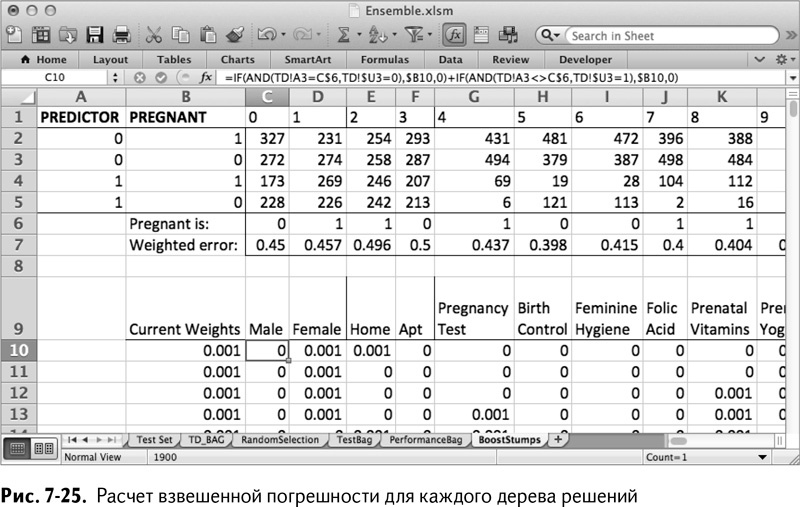
Выбираем победителя
Поместите в ячейку W1 название Winning Error, а в Х1 найдите минимальное значение взвешенной погрешности:
=MIN(C7:U7)
=МИН(C7:U7)
Как и в разделе про бэггинг, в Х2 нужно скомбинировать формулы INDEX/ИНДЕКС и MATCH/ПОИСКПОЗ, чтобы найти выигрышное дерево:
INDEX(C1:U1,0,MATCH(X1,C7:U7,0))
ИНДЕКС(C1:U1,0,ПОИСКПОЗ(X1,C7:U7,0))
А с помощью INDEX/ИНДЕКС и MATCH/ПОИСКПОЗ в Х3 можно узнать значение, ассоциирующееся с беременностью для этого дерева:
=INDEX(C6:U6,0,MATCH(X1,C7:U7,0))
=ИНДЕКС(C6:U6,0,ПОИСКПОЗ(X1,C7:U7,0))
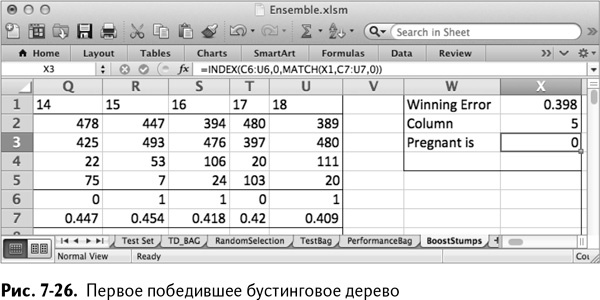
Так получается лист, изображенный на рис. 7-26. Начиная с одинаковых весов для каждой строки, признак номер 5 с индикатором беременности 0 выбран лучшим деревом. Вернувшись на лист TD, видим, что этот признак – противозачаточные.
Расчет альфа-значения для дерева
Бустинг работает, назначая веса обучающим строкам, которые были неправильно классифицированы предыдущими деревьями. Деревья в начале процесса бустинга в целом более эффективны, в то время как деревья в конце обучающего процесса – более специализированные, так как веса меняются для концентрации на нескольких неприятных точках обучающих данных.
Эти деревья со специализированными весами помогают в подгонке модели к странным точкам набора данных. Однако при этом их взвешенная погрешность будет больше, чем у деревьев в начале бустинга. Так как их взвешенная погрешность растет, общее улучшение, которое они вносят в модель, падает. В бустинге это соотношение выражается с помощью величины, которая называется альфа:
альфа = 0,5 × ln((1 – общая взвешенная погрешность дерева) /общая взвешенная погрешность дерева)
Так как общая взвешенная погрешность дерева растет, выражение под знаком натурального логарифма уменьшается и приближается к 1. А так как натуральный логарифм 1 равен 0, значение параметра альфа все уменьшается и уменьшается. Посмотрим на это в таблице.
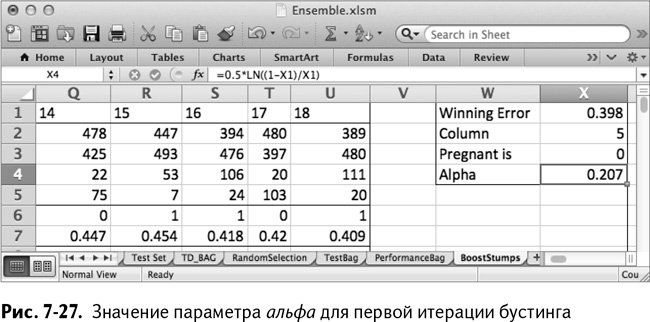
Назовите ячейку W4 Alpha, а в Х4 поместите взвешенную погрешность из Х1, подставленную в расчет параметра альфа:
=0,5*LN((1-X1)/X1)
Для этого первого дерева значение альфа в итоге получается равным 0,207 (рис. 7-27).
Как именно используются эти значения параметра альфа? В бэггинге каждое дерево имело голос 0/1 для прогнозирования. При прогнозировании для бустингованных деревьев каждый классификатор вместо этого выдает значение альфа, если считает, что покупатель беременный, и – альфа, если нет. Так что это первое дерево во время голосования в тестовых данных будет давать 0,207 каждому покупателю, не купившему противозачаточные и –0,207 каждому купившему. Итоговый прогноз ансамбля моделей – это сумма всех этих положительных и отрицательных значений параметра альфа.
Как вы увидите позже, чтобы определить общий прогноз беременности, выданный моделью, нужно установить границу на сумму баллов конкретного дерева. Поскольку в качестве своего вклада в прогноз каждое дерево выдает либо положительное, либо отрицательное значение альфа, в качестве классификационного порога принято использовать 0, однако вы можете менять его, дабы достичь большей точности.
Повторное взвешивание
Теперь, когда вы закончили с одним деревом, пришло время заново взвесить обучающие данные. Для этого нужно узнать, какие строки данных это дерево обрабатывает правильно, а какие – нет.
Поэтому в столбце V озаглавьте ячейку V9 Wrong. В V10 можно использовать формулу OFFSET/СМЕЩ вместе с номером столбца выигравшего дерева (ячейка Х2), чтобы найти взвешенную погрешность обучающей строки. Если погрешность не нулевая, то значит, дерево неправильно обработало строку и в столбец Wrong записывается единица:
=IF(OFFSET($C10,0,$X$2)>0,1,0)
=ЕСЛИ(СМЕЩ($C10,0,$X$2)>0,1,0)
Эту формулу можно раскопировать во все обучающие строки (обратите внимание на абсолютные ссылки!).
Теперь исходные веса для этого дерева находятся в столбце В. Чтобы отрегулировать их согласно тому, какие строки получили 1 в столбце Wrong, бустинг умножает исходный вес на exp(альфа*Wrong) (где eхp – экспоненциальная функция, с помощью которой вы делали логистическую регрессию в главе 6).
Если значение в столбце Wrong равно 0, то exp(альфа*Wrong) становится 1, и вес остается прежним.
Если в столбце Wrong единица, то exp(альфа*Wrong) имеет значение больше 1, поэтому общий вес увеличивается. Назовите столбец W Scale by Alpha. В W10 можно будет рассчитать этот новый вес следующим образом:
=$B10*EXP($V10*$X$4)
Раскопируйте эту формулу на всю последовательность.
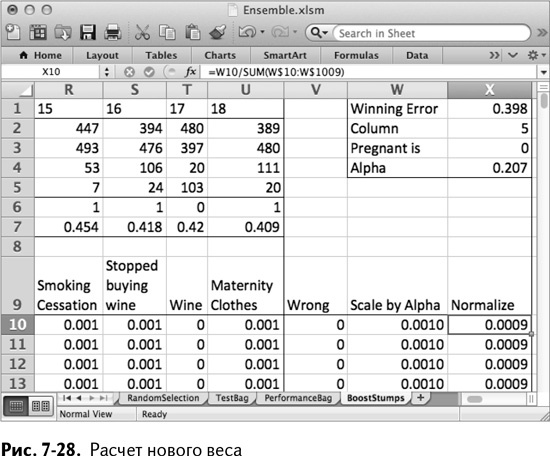
К сожалению, эти новые веса уже не образуют в сумме 1, как исходные. Их нужно нормализовать (отрегулировать так, чтобы в сумме они все же давали 1). Поэтому назовите ячейку Х9 Normalize, а в Х10 разделите новый вес на сумму всех новых весов:
=W10/SUM(W$10:W$1009)
=W10/СУММА(W$10:W$1009)
Теперь можно быть уверенным, что сумма новых весов – 1. Раскопируйте формулу. В итоге получается лист, изображенный на рис. 7-28.
И еще разок. И еще…
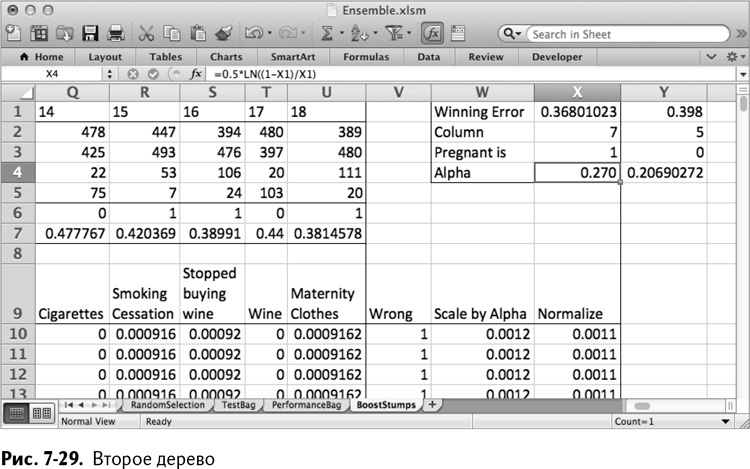
Теперь вы готовы построить второе дерево. Сначала скопируйте данные выигравшего дерева из предыдущей итерации от X1:X4 до Y1:Y4.
Теперь скопируйте новые значения весов из столбца Х в столбец В. Весь лист обновится, чтобы выбрать лучшее дерево для нового набора весов. Как показано на рис. 7-29, второе выигравшее дерево имеет номер 7 (фолиевая кислота), и 1 в нем обозначает беременность.
Вы можете обучить эти 200 деревьев примерно таким же способом, как мы это делали в бэггинге. Просто запишите макрос, который вставляет новый столбец Y, копирует значения из Х1:Х4 в Y1:Y4 и переносит веса из столбца Х в столбец В.
После 200 итераций ваша взвешенная погрешность возрастет почти до 0,5, в то время как значение альфа упадет до 0,005 (рис. 7-30). Вспомните, что ваше первое дерево имело значение альфа, равное 0,2. Это означает, что деревья в конце процесса в 40 раз слабее в голосовании, чем самое первое дерево в начале.
Оценка модели бустинга
Ну вот! Вы обучили целую бустинговую модель деревьев принятия решений. Вы можете сравнить ее с моделью бэггинга, взглянув на ее параметры качества. Для этого сначала сделайте прогнозы с помощью модели на тестовых данных.
Прогнозы на тестовой выборке
Заготовьте копию тестовой выборки и назовите ее TestBoost, а затем вставьте четыре пустые строки в верхнюю часть листа, чтобы потом записать туда ваши победившие деревья. Начиная со столбца W на листе TestBoost вставьте ваши деревья (в моем случае 200) в верх листа. Так получается лист, изображенный на рис. 7-31.
В ячейке W6 вы можете оценить первое дерево на первой строке тестовых данных с помощью OFFSET/СМЕЩ точно так же, как в модели бэггинга. За исключением того, что в этот раз прогноз беременности выдает значение альфа данного дерева (ячейка W4), а прогноз ее отсутствия – минус альфа.
=IF(OFFSET($A6,0,W$2)=W$3,W$4,-W$4)
=ЕСЛИ(СМЕЩ($A6,0,W$2)=W$3,W$4,-W$4)
Скопируйте эту формулу на все деревья и на все строки тестовых данных (рис. 7-32). Чтобы сделать прогноз для строки, сложите эти значения по всем прогнозам ее дерева.
Назовите V5 Score (баллы). Количество баллов в V6 – это просто сумма прогнозов, данных справа:
=SUM(W6:HN6)
=СУММА(W6:HN6)
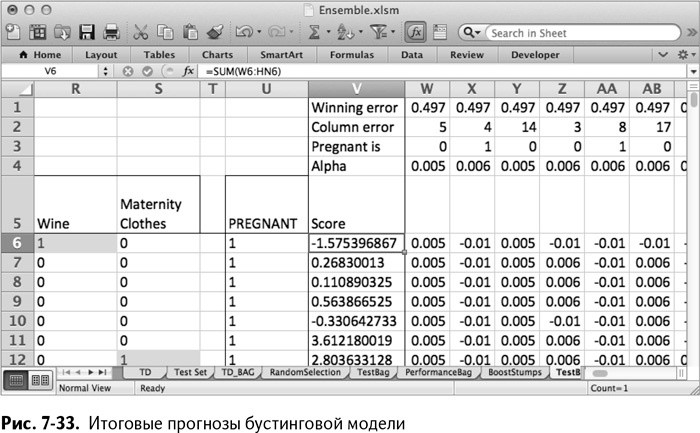
Скопируйте эту сумму на весь столбец. У вас получится лист вроде изображенного на рис. 7-33. Баллы в столбце V больше нуля означают, что больше альфа-взвешенных прогнозов ушло в положительном направлении, чем в отрицательном (рис. 7-33).
Рассчитываем качество работы
Чтобы измерить качество работы модели бустинга на тестовой выборке, создайте копию листа PerformanceBag и назовите ее PerformanceBoost. Укажите на столбец V листа TestBoost и установите граничные значения на возрастание от минимума баллов бустинговой модели до максимума. В моем случае я делаю это с шагом в 0,25 между минимальным значением прогноза в –8 и максимальным 4,5. Так получается лист качества работы, изображенный на рис. 7-34.
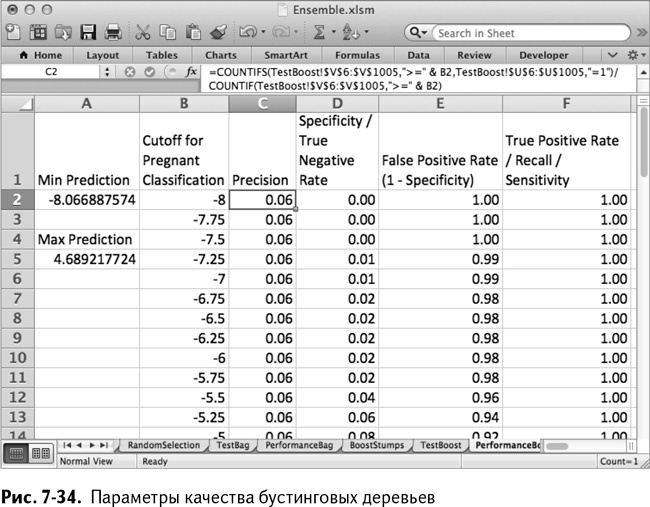
На этой модели мы видим, что граничное значение баллов, равное 0, дает 85 % положительных результатов и только 27 % ложноположительных. Неплохо для 200 тупых деревьев!
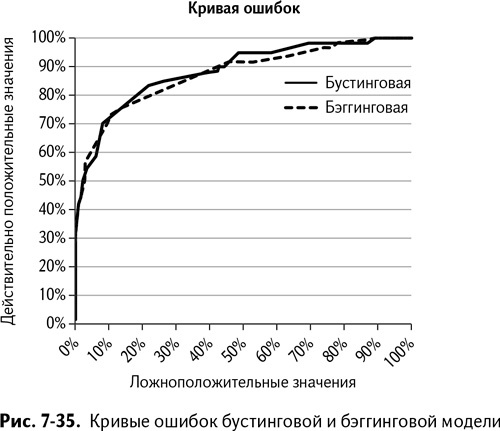
Добавьте кривую ошибок модели бустинга к кривой ошибок бэггинговой модели, чтобы сравнить их, как мы сравнивали модели в главе 6. Как явствует из рис. 7-35, бустинговая модель опережает бэггинговую во многих точках.
Кое-что кроме качества
В целом, чтобы сделать хорошую бустинговую модель требуется меньше деревьев, чем для модели бэггинга. Этот метод не так популярен, как бэггинг, потому что риск переподгонки данных немного выше. Так как каждое переписывание обучающих данных основано на неверно классифицированных в предыдущей итерации точках, в итоге можно оказаться в ситуации, когда обученные вами классификаторы становятся чрезвычайно чувствительными к выбросам.
К тому же итеративное повторное взвешивание данных означает, что бустинг, в отличие от бэггинга, не может быть запараллелен на несколько компьютеров или ядер процессора.
Таким образом, в гонке между хорошо подогнанными бустинговой и бэггинговой моделями последней победа оказалась не по зубам.
Назад: Нужно еще сильнее!
Дальше: Подытожим

