Книга: Много цифр. Анализ больших данных при помощи Excel
Назад: Не обольщайтесь!
Дальше: Предсказание беременных покупателей РитейлМарта с помощью логистической регрессии
Определение беременных покупателей РитейлМарта с помощью линейной регрессии
Заметка
Таблица Excel, использованная в этой главе, RetailMart.xlsx, доступна для скачивания вместе с книгой на сайте издательства www.wiley.com/go/datasmart. Она содержит все вводные данные, которые вам потребуются для работы. Вы также можете просто следить за ходом повествования, поглядывая на картинки, в которых я все уже сделал за вас.
Представьте, что вы – менеджер по рекламе в головном офисе РитейлМарта и отвечаете за детские товары. Ваша обязанность – способствовать продажам как можно большего количества подгузников, молочной смеси, ползунков, кроваток, колясок, сосок и т. д. молодым родителям. У вас есть небольшая проблема.
Из данных фокус-групп вы знаете, что у супругов, ожидающих прибавления, и родителей новорожденных покупка детских товаров легко входит в привычку. Они практически сразу находят подгузники, которые им нравятся, и магазины, в которых они дешевле всего. Они находят соску, которая нравится их ребенку, и уже знают, где купить экономичную упаковку. Вы хотите, чтобы РитейлМарт стал первым магазином на их пути. И хотите максимизировать его шансы стать для этих людей магазином детских товаров № 1.
Но для этого необходимо, чтобы родители увидели вашу рекламу до того, как купят свою первую упаковку подгузников где-то еще. Они должны узнать о вас еще до рождения ребенка. Едва он появится на свет, родители получают ваш купон на подгузники и присыпку и, возможно, даже успеют им воспользоваться.
Из этого можно сделать простой вывод: вам нужна прогностическая модель, способная определить потенциально беременных покупательниц для дальнейшего целевого маркетинга.
Набор отличительных признаков
В вашем арсенале есть секретное оружие для построения такой модели – данные учетных записей покупателей. Конечно, это далеко не все покупатели вашего магазина – шансы достучаться до молодожена, живущего в лесу и расплачивающегося наличными, практически равны нулю. Но что касается обладателей кредитки вашего магазина или учетной записи в вашем интернет-магазине с привязанной к ней кредиткой, то их заказы можно смело относить не только к покупателям лично, но и к их семьям.
Так или иначе, вы не можете просто взять и загрузить в модель ИИ всю историю покупок как есть, неструктурированную, и ждать, что что-то произойдет. Вам бы неплохо догадаться выудить оттуда релевантные признаки нужных покупателей. Следует задаться вопросом: «Какие покупки совершает семья, в которой ждут пополнения, а какие – семья, в которой не ждут?»
Первое, что приходит в голову – это тест на беременность. Если покупательница заказывает тест, то ее вероятность оказаться беременной выше, чем у среднестатистического клиента онлайн-магазина. Такие признаки часто называются features – отличительные черты, или независимые переменные, ведь, то, что мы пытаемся определить – «Беременна (да/нет)?» является зависимой переменной, в том смысле, что ее значение будет зависеть от данных, содержащихся в независимых переменных, которые мы и загружаем в модель.
Отвлекитесь на минутку и прикиньте, какие возможные отличительные признаки могли бы подойти к этой модели ИИ. Какие истории заказов стоит в нее загружать?
Вот мой список примерных отличий, который можно составить по заказам покупателей, а потом проассоциировать их с информацией из учетных записей:
• пол владельца учетной записи – мужской/женский/не указано; фамилию можно сравнить с данными переписи населения;
• адрес владельца учетной записи – частный дом, квартира или абонентский ящик;
• недавно заказывал тест на беременность;
• недавно заказывал противозачаточные;
• недавно заказывал средства женской гигиены;
• недавно заказывал препараты с фолиевой кислотой;
• недавно заказывал витамины для беременных;
• недавно заказывал DVD йоги для беременных;
• недавно заказывал подушку для тела;
• недавно заказывал имбирный эль;
• недавно заказывал браслеты от укачивания;
• регулярно заказывал сигареты до недавнего времени, затем перестал;
• недавно заказывал сигареты;
• недавно заказывал продукты для бросающих курить (жвачку, пластырь и т. д.);
• регулярно заказывал вино до недавнего времени, затем перестал;
• недавно заказывал вино;
• недавно заказывал одежду для беременных или кормящих.
Ни один из этих признаков не идеален. Люди не заказывают в РитейлМарте каждую мелочь, Они могли купить тест на беременность в ближайшей аптеке, а не у вас, а препараты для беременных получить по назначению врача. Но даже если покупатель заказывает в РитейлМарте решительно все, в семьях, ожидающих детей, все равно может быть курящий или пьющий человек. Одежду для беременных зачастую носят совсем не беременные девушки, особенно если в моде завышенная талия – слава Богу, в романе Джейн Остин не было РитейлМарта. Имбирный эль помогает от тошноты, но также хорош и с бурбоном. Такова общая картина.
Ни один из этих признаков не ограничивает нашу модель, но есть надежда на то, что их объединенные силы сработают в стиле Капитана Планета и тогда модель сможет классифицировать покупателей сравнительно точно.
Сборка обучающих данных
По данным проведенных компанией опросов, 6 % семей покупателей РитейлМарта ждут прибавления в любой момент времени. Вам нужно выбрать несколько образцов из этой группы в базе данных РитейлМарта и собрать из их историй заказов признаки для модели, причем еще до того, как родятся дети. Таким же образом вы должны собрать эти признаки для примеров покупателей, не ожидающих прибавления.
Набрав с помощью этих отличий по пачке семей ожидающих и не ожидающих детей, вы можете их использовать как примеры для обучения модели ИИ.
Но как быть с семьями, уже имеющими детей? Всегда есть вариант опроса покупателей для построения обучающей последовательности. Но сейчас вы просто делаете прототип, так что можете позволить себе считать семьи с уже родившимися детьми подходящими для изучения их покупательских привычек. Покупателей, внезапно начавших покупать подгузники для новорожденных и продолжающих время от времени покупать подгузники все большего размера хотя бы год, резонно считать таковыми.
Таким образом, просматривая историю заказов покупателей до первой покупки подгузников, можно выбрать отличительные признаки «беременных» семей, перечисленные выше. Представьте, что вы выбрали 500 таких семей и извлекаете информацию об их отличиях из базы данных РитейлМарта.
Что же касается «не-беременных» покупателей, то из базы данных вы можете извлекать историю покупок любых случайно выбранных клиентов РитейлМарта, которые не удовлетворяют критерию «постоянного заказа подгузников». Конечно, одна или две «беременные» семьи могут просочиться в «не-беременную» категорию, но так как «беременные» семьи составляют очень малый процент от общего количества покупателей РитейлМарта (и это еще до исключения покупателей подгузников), эта случайная выборка должна быть достаточно чиста. Представьте, что выбрали еще 500 примеров таких «не-беременных» семей.
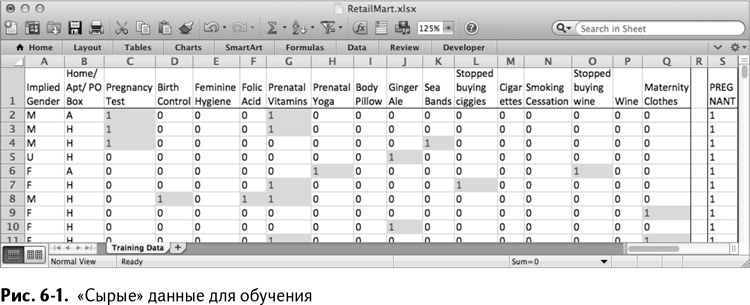
Составленная из этих данных таблица в 1000 строк (500 беременных, 500 «не-беременных») в Excel будет выглядеть, как изображено на рис. 6–1.
Решение проблемы классового дисбаланса
Теперь вы знаете, что беременными в любой момент являются всего 6 % нашей «дикой» популяции покупателей, хотя в обучающей последовательности это соотношение – 50/50. Это называется выборкой с запасом. Беременность была бы меньшинством, «редким классом» данных, а сбалансировав образец, мы бы получили классификатор, заваленный данными о «не-беременных» покупателях. В конце концов, если вы оставите разделение естественным – 6/94, то простое объявление всех и каждого «не-беременным» даст нам те же 94 % с учетом точности. Это опасно: ведь беременные – это, хоть и малочисленный, но все же интересующий вас класс, маркетингом в котором вы и занимаетесь.Такая балансировка обучающих данных внесет в них некоторый сдвиг – модель «решит», что беременность встречается гораздо чаще, чем на самом деле. Но это не проблема, потому что в данном случае нас не интересует настоящая вероятность забеременеть. Как явствует ниже, главное – найти точку пересечения «очков» по беременности, выданных моделью, между положительными и ложноположительными результатами.
В первых двух столбцах обучающих данных стоят категорийные данные пола и типа адреса. Остальные признаки бинарны, и 1 означает ПРАВДА. Так, к примеру, взглянув на первую строку таблицы, вы увидите, что этот покупатель считается беременным (столбец S). Это как раз тот столбец, значения в котором и должна научиться предсказывать ваша модель. Заглянув в историю заказов этого покупателя, вы найдете в ней тест на беременность и пару банок витаминов для беременных. Также эти семьи не заказывали в последнее время вино и сигареты.
Пролистав данные, вы увидите все типы покупателей: у кого-то множество индикаторов, а у кого-то всего пара. Как и ожидалось, семьи в ожидании детей все же покупают время от времени вино и сигареты, а бездетные – заказывают товары, ассоциирующиеся с беременностью.
Создание фиктивных переменных
Вы можете считать, что модель ИИ – просто формула и ничего больше, она берет цифры, немного «жует» их и «выплевывает» прогноз, который должен выглядеть примерно как 1 (беременна) и 0 (нет) в столбце S нашей таблицы.
Но проблема с вводными данными состоит в том, что первые два столбца вообще не являются числами. Они представлены в виде букв, обозначающих категории, например мужчину и женщину.
Такая проблема – работа с категорийными данными, то есть с данными, сгруппированными в конечное число понятий без присвоения им числовых эквивалентов, – частенько настигает тех, кто работает над извлечением данных. Если вы разошлете своим покупателям опросник, в котором они должны будут написать, в какой сфере они работают, свое семейное положение, страну проживания, породу своей собаки или название любимой серии «Девочек Гилмор», то вы завязнете в обработке категорийных данных.
Это некая противоположность числовым данным, которые уже выражены цифрами и готовы к поглощению технологиями добычи данных.
Так что же нужно сделать с категорийными данными, чтобы можно было с ними работать? Если коротко, то вы должны превратить их в числовые.
Иногда категорийные данные сами расположены в некотором порядке, который можно использовать для присвоения каждой категории числового значения. К примеру, если бы в вашем наборе данных была переменная, обозначающая ответ на вопрос, водят ли опрашиваемые Scion, Toyota или Lexus, то вы могли бы просто обозначить их ответы 1, 2 и 3. Вот вам и цифры!
Но гораздо чаще встречаются категории, не имеющие порядка, например, пол. К примеру, мужчина, женщина и «не указано» – это отдельные категории без намека на порядковую нумерацию. В таких случаях, чтобы перевести категорийные данные в числовые, обычно используется техника под названием «фиктивная переменная», или «дамми» (dummy coding).
Фиктивная переменная работает следующим образом: берется один столбец с категорийными данными (рассмотрим столбец Implied Gender – «Пол») и разбивается на несколько бинарных столбцов. То есть вместо одного столбца Implied Gender у нас их три: один для мужчин, другой для женщин и третий – для не указавших свой пол. Если в исходном столбце значение ячейки было «М», то теперь вместо этого у нас есть 1 в столбце Male, 0 в столбце Female и 0 в столбце Unknown.
На самом деле здесь избыточное количество столбцов, потому что если и в столбце Male, и в столбце Female у вас 0, то уже подразумевается, что пол не указан. Вам не нужен третий столбец.
Таким образом, при использовании фиктивной переменной для кодирования категорийных данных вам всегда нужно на один столбец меньше, чем количество имеющихся у вас категорий – последняя категория может быть выражена через остальные. Говоря языком статистики, категорийная переменная пола имеет всего две степени свободы, так как степеней свободы всегда на одну меньше, чем возможных значений переменной.
В нашем конкретном примере стоит начать с копирования листа Training Data в новый лист под названием Training Data w Dummy Vars. Вы должны разделить первые два признака на два столбца каждый, так что смело стирайте все из столбцов А и В и вставляйте еще два пустых столбца слева от А.
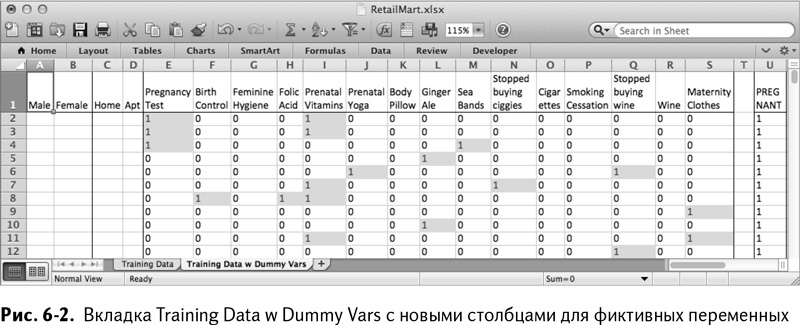
Назовите эти четыре пустых столбца Male, Female, Home и Apt (не указанный пол и абонентский ящик выражаются через остальные признаки). Как показано на рис. 6–2, теперь у вас должно быть четыре пустых столбца для размещения фиктивных переменных ваших двух категорийных переменных.
Рассмотрим первую строчку обучающих данных. Чтобы превратить «М» в столбце пола в значение фиктивной переменной, нужно поместить 1 в столбец Male и 0 в cтолбец Female. (Единица в столбце Male сама по себе означает, что пол не является «не указанным».)
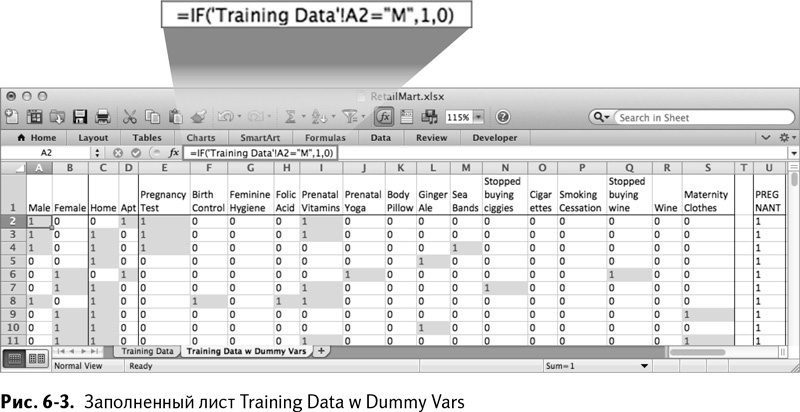
Проверьте старое значение категории во вкладке Training Data, и если это «М», то в ячейке А2 вкладки Training Data w Dummy Vars поставьте 1:
=IF(‘TrainingData’!A2=”M”,1,0)
=ЕСЛИ(‘TrainingData’!A2=”M”,1,0)
То же самое относится к значению «F» в столбце Female, H в столбце Home и А в столбце Apt. Чтобы раскопировать эти четыре формулы во все строки, вы можете либо перетащить их, либо (что предпочтительнее), как описывалось в главе 1, выделить их все и затем кликнуть дважды в правом нижнем углу ячейки D2. Это заполнит весь лист до D1001 конвертированными значениями переменных. Сконвертировав эти две категории в четыре бинарных фиктивных переменных (рис. 6–3), вы готовы к началу моделирования.
Мы сделаем свою собственную линейную регрессию!
Каждый раз, когда я так говорю, по крайней мере один работник статистики теряет крылья, но я все равно гну свое: если вы хоть раз проводили линию тренда через облако точек на диаграмме, то вы уже строили модель ИИ.
Вы, наверное, думаете: «Не может быть! Я бы знал, если бы создал робота, способного вернуться назад во времени и убить Джона Коннера!»
Простейшая линейная модель
Позвольте мне все объяснить с помощью простых данных на рис. 6–4.
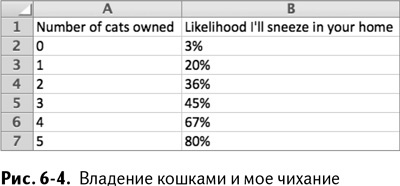
В изображенной таблице мы видим количество кошек в доме в первом столбце и вероятность того, что я буду в этом доме чихать, во втором. Никаких кошек? 3 % времени я все равно буду чихать от осознания того, что где-то все же существуют некие гипотетические кошки. Пять кошек? В таком случае я практически гарантированно буду чихать. А теперь мы можем сделать из этих данных точечную диаграмму в Excel и взглянуть на нее или на рис. 6–5 (больше информации о вставке диаграмм и графиков вы найдете в главе 1).
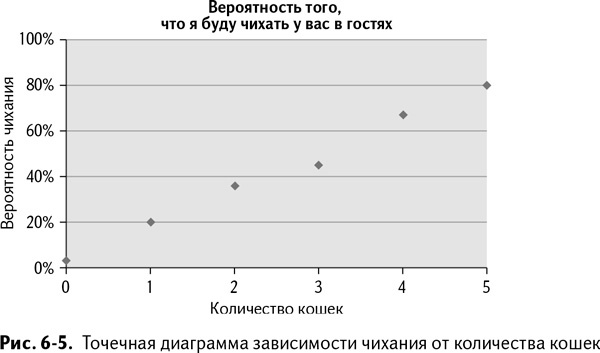
Кликая правой клавишей на точки диаграммы (нужно кликать прямо на точки, а не на поле диаграммы) и выбирая в меню «Добавить линию тренда», вы можете выбрать и добавить на график линейную регрессионную модель. В разделе «Параметры» окна «Линии тренда» выберите «Показывать уравнение на диаграмме». Нажав «ОК», вы увидите и линию тренда, и формулу для нее (рис. 6–6).
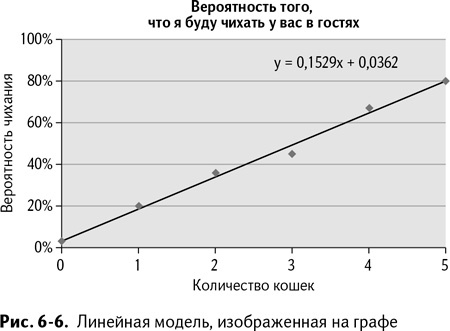
Линия тренда на графике ясно показывает зависимость между чиханием и количеством кошек, которая описывается формулой:
Y = 0,1529x + 0,0362
Другими словами, если х равен нулю, то линейная модель думает, что у меня есть 3–4 %-ный шанс чихнуть и за каждую кошку щедро дает 15 % сверху.
Начальная точка графика на оси вероятности расположена на уровне 3–4 %, что называется начальным отрезком, или свободным членом функции, а 15 % за кошку – коэффициент переменной кошек. Предположения такого рода не требуют ничего, кроме будущих данных, которые затем комбинируются с коэффициентом и начальным отрезком модели.
На самом деле, при желании вы можете скопировать из графика формулу «= 0,1529x + 0,0362» и вставить ее в ячейку, чтобы делать прогнозы, подставляя вместо x подходящие числа. К примеру, в будущем я зайду в дом с тремя с половиной кошками внутри (бедняга Тимми потерял свои задние лапы в лодочной аварии), затем вычислю «линейную комбинацию» коэффициентов и своих данных, добавлю начальный отрезок и получу свой прогноз:
0,1529 * 3,5 cats + 0,0362 = 0,57
57 %-ный шанс чихнуть! Это является моделью ИИ в том смысле, что мы взяли независимую переменную (кошек), зависимую переменную (чихание) и попросили компьютер описать их взаимоотношения формулой, которая больше всего похожа на данные о событиях в прошлом.
Теперь вам, наверное, интересно, как компьютер догадался, какая у этих данных линия тренда. Она неплохо выглядит, но откуда он знает, как? Выражаясь более человеческим языком, компьютер искал такую линию тренда, которая бы лучше всего подходила к данным, то есть чтобы сумма квадратов отклонений от данных была минимальной.
Чтобы понять, зачем нам сумма квадратов отклонений и что она означает, подставим в уравнение линии тренда одну кошку:
0,1529 * 1 cat + 0,0362 = 0,1891
Обучающие данные дают нам здесь вероятность 20 %, а не 18,91. Таким образом, отклонение линии тренда в этой точке от данных равна 1,09 %. Величина отклонения возводится в квадрат, чтобы ее значение было положительным, независимо от того, по какую сторону от линии тренда оказалась наша точка. 1,09 % в квадрате дают 0,012 %. А если мы теперь сложим все квадраты отклонений от всех известных нам точек обучающих данных, у нас получится сумма квадратов отклонений (которую часто называют просто суммой квадратов). И это именно то, что Excel минимизирует, когда подгоняет линию тренда под график чихания.
Хотя в ваших данных из РитейлМарта слишком много измерений, чтобы делать из них точечную диаграмму, в следующих разделах мы будем подгонять к нашим данным точно такую же линию.
Вернемся к данным РитейлМарта
Ну что ж, пришло время построить линейную модель вроде кошкочихательной на основе данных РитейлМарта. Для начала создайте новый лист и назовите его Linear Model, а затем вставьте туда данные из Training Data w Dummy Vars, начиная со столбца В и строки 8 – нужно оставить место вверху таблицы для коэффициентов линейной модели и других оценочных данных, за которыми вы будете следить.
Чтобы сохранить порядок, вставьте снова строку с названиями в строку 1. В столбце U добавьте заголовок Intercept, потому что ваша линейная модель, как и предыдущая, будет начинаться не в нуле. Более того, чтобы было проще вставить в модель свободный член, заполните столбец Intercept (U8:U1007) единицами. Это позволит вам обсчитать модель, применяя функцию SUMPRODUCT/СУММПРОИЗВ к строке коэффициентов и строке данных, что непременно потребует участия свободных членов.
Все коэффициенты этой модели мы поместим в строку 2, так что озаглавьте ее Model Coefficients и запишите стартовые значения, равные единице, в каждую ее ячейку. Вы также можете воспользоваться условным форматированием строки коэффициентов, чтобы увидеть изменения, когда они появятся.
Теперь ваши данные выглядят так, как показано на рис. 6–7.
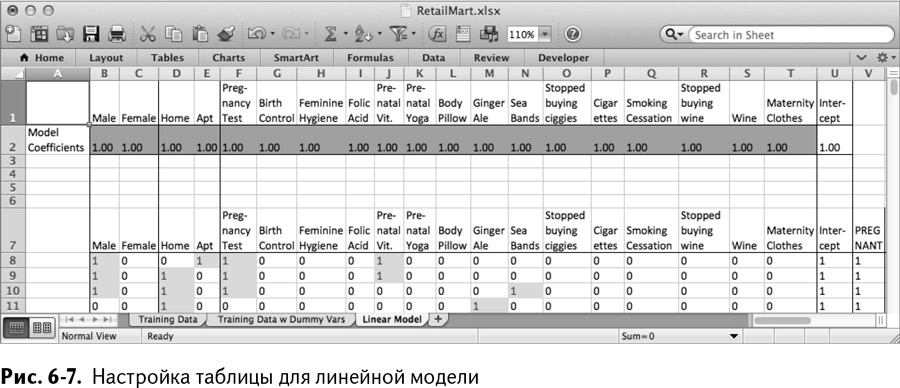
После установки коэффициентов в строке 2 можно вычислить линейную комбинацию коэффициентов (формула SUMPRODUCT/СУММПРОИЗВ) со строкой данных покупателя и получить прогноз о беременности.
Получилось слишком много столбцов, чтобы рисовать такой же график, как в случае с кошками, так что придется вам обучать модель самим. Первый шаг в этом нелегком деле – добавление в таблицу столбца с прогнозом, в котором уже содержится одно готовое значение для какой-нибудь строки.
В столбец W, следующий за данными покупателей, добавьте название Linear Combination (Prediction) в строку 7, а ниже поместите линейную комбинацию коэффициентов и данных покупателей (свободный член включен). Формула, которую вы вставляете в строку 8, чтобы проделать это с первым покупателем, выглядит так:
=SUMPRODUCT(B$2:U$2,B8:U8)
=СУММПРОИЗВ(B$2:U$2,B8:U8)
Поместите в строку 2 абсолютную ссылку, чтобы можно было перетащить формулу вниз, распространив на всех покупателей, без изменения коэффициентов в строках.
Подсказка
Кроме того, вы можете выделить столбец W, кликнуть на нем правой клавишей мышки, выбрать «Форматирование ячеек» и отформатировать значения в них как числа с двумя знаками после запятой, что впоследствии убережет вас от сердечного приступа при виде их огромного количества.
После добавления столбца ваша таблица будет выглядеть, как показано на рис. 6–8.
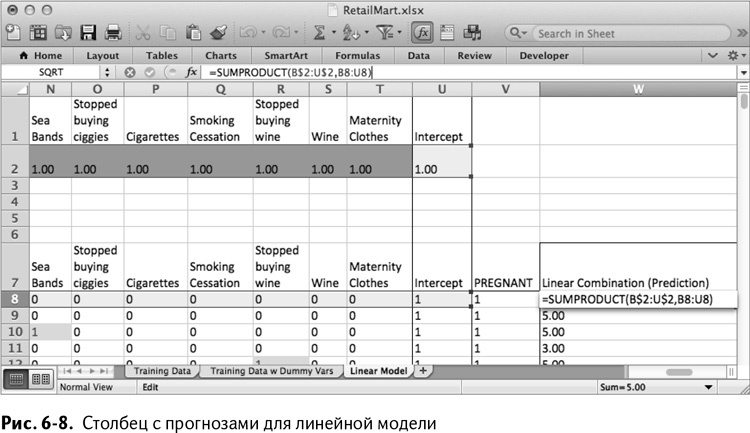
В идеале столбец с прогнозами (W) должен был бы содержать данные, совпадающие с теми, о которых известно, что они верны (столбец V), но использование единицы как коэффициента для каждой переменной дает неожиданный результат. Первый же покупатель получает прогноз, равный 5, при том, что беременность определяется 1, а ее отсутствие – 0. Что значит 5? Очень-очень беременна?
Добавляем учет отклонений
Вам нужно заставить компьютер определить коэффициенты модели за вас, но чтобы научить его это делать, придется дать машине понять, когда прогноз правильный, а когда – нет.
Для этого добавьте расчет отклонений в столбец Х. Используйте квадрат отклонения, который есть не что иное, как квадрат расстояния от значения Pregnancy (беременность, столбец V) до прогнозируемого значения (столбец W).
Возведение в квадрат позволяет каждому отклонению быть положительным, чтобы вы смогли затем сложить их все вместе и получить общее отклонение для модели. И здесь вам совершенно не нужны положительные и отрицательные значения отклонения, уничтожающие друг друга при сложении. Поэтому для первого покупателя в таблице у вас будет следующая формула:
=(V8-W8)^2
Вы можете растянуть эту ячейку вниз на весь столбец, чтобы у каждого покупателя был свой расчет отклонений.
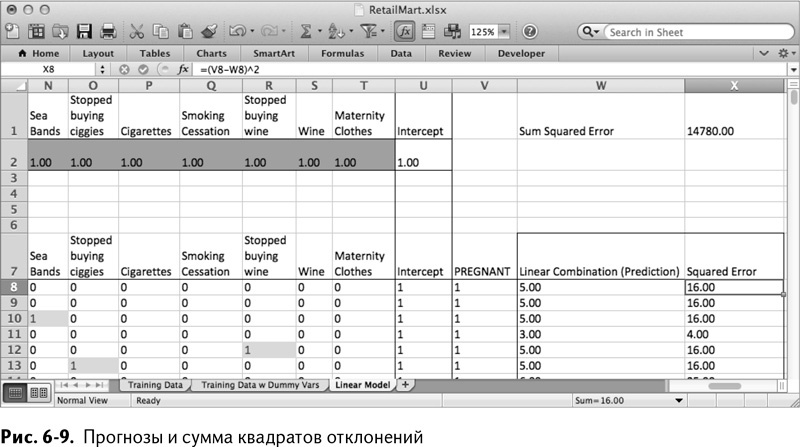
А теперь добавьте ячейку над прогнозами в Х1 (обозначенную в W1 как Sum Squared Error – сумма квадратов отклонений), в которой будет подсчитываться сумма значений столбца квадратов отклонений с помощью следующей формулы:
=SUM(X8:X1007)
=СУММА(X8:X1007)
Ваша таблица теперь выглядит, как показано на рис. 6–9.
Обучение «Поиском решения»
Теперь вы готовы к обучению вашей линейной модели. Нужно установить такие коэффициенты, чтобы сумма квадратов отклонений была как можно меньше. Если вам слышится что-то похожее на формулировку для «Поиска решения», то вы правы – это она. Точно так же, как в главе 2, а также 4 и 5, вам нужно открыть «Поиск решения» и заставить компьютер найти для вас лучшие коэффициенты.
Вашей целевой функцией будет сумма квадратов отклонений в ячейке Х1, которую вы хотите минимизировать «изменением значений переменных» в ячейках от В2 до U2, которые, в свою очередь, являются коэффициентами в вашей модели.
Далее, квадрат отклонения – это квадратичная функция ваших переменных решения, коэффициентов, поэтому для решения вы не можете воспользоваться линейным симплекс-методом, как в главе 4. Симплекс-метод работает очень быстро и гарантированно находит наилучшее решение, но модель понимает только линейные комбинации решений. Для «Поиска решения» вам потребуется эволюционный алгоритм.
Справка
Более развернутую информацию о нелинейных моделях оптимизации и внутреннем устройстве эволюционного алгоритма вы можете найти в главе 4. Если хотите, можете также поиграть с нелинейным оптимизационным алгоритмом в Excel под названием GRG.
По сути, «Поиск решения» будет выискивать такие значения коэффициентов, которые заставляют сумму квадратов уменьшаться, пока ему не покажется, что найдено действительно хорошее решение. Чтобы эффективно использовать эволюционный алгоритм, нужно установить нижнюю и верхнюю границы. Чем ближе они друг к другу (но не слишком близко!), тем лучше работает алгоритм. Для этой модели я установил их на –1 и 1.
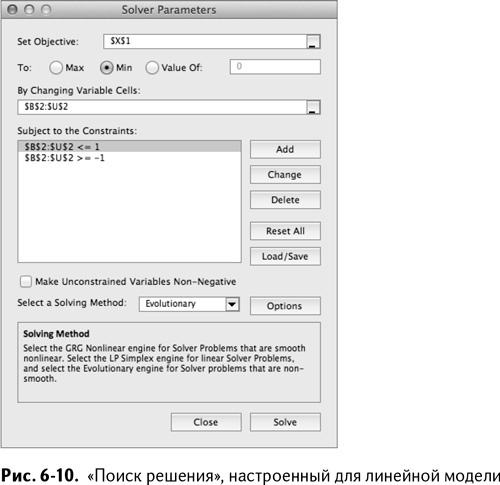
Когда вы с ними разберетесь, настройка вашего «Поиска решения» будет выглядеть примерно, как показано на рис. 6-10.
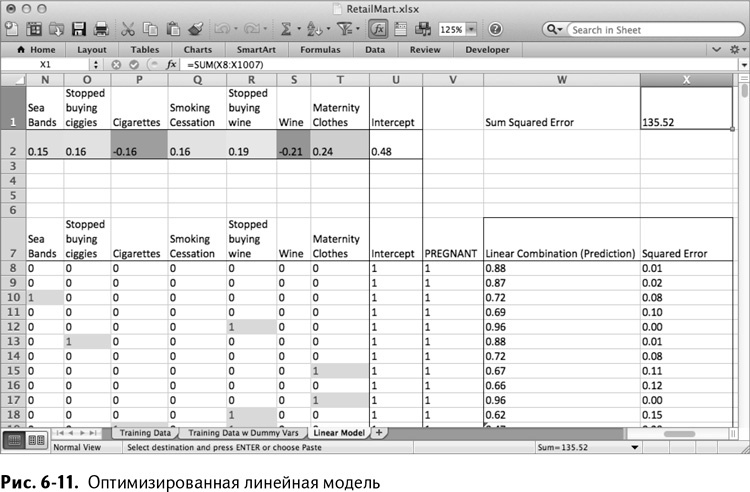
Нажмите «Выполнить» и ждите! Пока «Поиск решения» пробует различные коэффициенты для модели, вы увидите, как меняются их значения. Условное форматирование ячеек даст вам почувствовать разброс. Более того, сумма квадратов отклонений будет становиться то больше, то меньше, но в конечном итоге уменьшится. По окончании работы «Поиск решения» сообщит вам, что задача оптимизирована. Нажмите «ОК» и возвращайтесь к модели.
На рис. 6-11 вы видите, что «Поиск решения» закончил с результатом 135,52 – вот чему оказалась равна сумма квадратов отклонений. Если вы повторяете за мной и запускаете свой «Поиск решения», то имейте в виду: два разных запуска эволюционного алгоритма никогда не закончатся одним и тем же значением – ваша сумма квадратов в конце концов может оказаться больше или меньше моей, да и коэффициенты модели в итоге могут немного отличаться. Оптимизированная линейная модель показана на рис. 6-11.
Использование формулы LINEST/ЛИНЕЙН для линейной регрессии
Некоторые читатели наверняка в курсе, что у Excel есть своя формула линейной регрессии – LINEST/ЛИНЕЙН. Одним махом эта формула, безусловно, может сделать то, что вы только что делали вручную. Однако при 64 отличительных признаках моделирования она вылетает, так что действительно большие регрессии вам все равно придется делать самим.Задействуйте формулу LINEST/ЛИНЕЙН применительно к нашей модели. Но будьте внимательны! Прочитайте справочный раздел Excel об этой формуле. Чтобы достать оттуда все свои коэффициенты, вам необходимо воспользоваться формулой массива (подробнее в главе 1). Имейте в виду: она выдает коэффициенты в обратном порядке (Male будет последним коэффициентом перед свободным членом), что очень раздражает.А вот где она действительно незаменима, так это в автоматическом вычислении многих значений, необходимых для выполнения статистической проверки вашей линейной модели, таких как запутанные расчеты коэффициента стандартного отклонения, которые вы встретите в следующем разделе.Но в этой главе вам придется делать все вручную, так что ваши новые знания о замечательной функции LINEST/ЛИНЕЙН (и функциях линейного моделирования других программных пакетов) просто должны помочь вам расслабиться – в будущем вы сможете смело на них положиться. К тому же ручная работа облегчает переход к логистической регрессии, которая не поддерживается Excel.
Использование медианной регрессии для работы с выбросами
В медианной регрессии минимизируется сумма абсолютных значений отклонений, вместо суммы их квадратов. И это единственное отличие от линейной регрессии.Зачем она вам?В случае с линейной регрессией выбросы (значения, сильно отстоящие от остальных) вашего обучающего набора данных довольно ощутимо «оттягивают» на себя модель в процессе подгонки тренда. Если их отклонения достаточно велики, линейная регрессия будет больше «прогибаться» в сторону баланса между их большим отклонением и отклонениями остальных точек графика, чем при балансе, заложенном в медианной регрессии. В последнем случае линия, подходящая к данным, будет оставаться ближе к типичным входящим в модель данным, чем тяготеть к выбросам.Я не планирую затрагивать в этой главе медианную регрессию. Вы можете попробовать воспользоваться ею сами – в этом нет ничего сложного. Просто замените квадрат отклонения абсолютным значением (в Excel есть функция ABS) – и все готово к старту!Это означает, что если вы работаете в Windows и у вас установлен OpenSolver (см. главу 1), то у вас появилась большая проблема!Так как в медианной регрессии мы минимизируем отклонения, а абсолютное значение может также быть и максимумом функции (максимальным ее значением и –1, умноженной на это значение), попробуйте линеаризировать медианную регрессию в стиле модели минимакса (более подробно оптимизационная модель минимакса описана в главе 4). Подсказка: вам нужно будет создать по одной переменной на строку данных, поэтому придется использовать OpenSolver – встроенный в Excel «Поиск решения» не справится с тысячью решений и двумя тысячами переменных.Удачи!
Статистика линейной регрессии: R-квадрат, критерии Фишера и Стьюдента
Заметка
Следующий раздел – самый замысловатый во всей книге. Он, без сомнения, содержит самые сложные вычисления – расчет стандартного отклонения коэффициентов модели. Я постарался объяснить все как можно доходчивее, но некоторые вычисления требуют объяснений на уровне, соответствующем сложности текста. А я не хочу здесь отвлекаться на курс лекций по линейной алгебре.Постарайтесь вникнуть в эти понятия насколько возможно. Применяйте их на практике. А если хотите узнать больше – возьмите учебник по математической статистике начального уровня (к примеру, «Статистика простым языком» – Statistics in Plain English by Timothy C. Urdan [Routledge, 2010]).Если вы все же застрянете – знайте, что к этой главе в остальной книге ничего не привязано. Пропустите ее, а потом вернитесь, если понадобится.
Итак, у нас есть линейная модель, которую мы подгоняем, минимизируя сумму квадратов. Если взглянуть на прогнозы в столбце Y, то, на первый взгляд, они кажутся вполне похожими на правду. К примеру, беременная покупательница в строке 27, заказавшая тест на беременность, витамины для беременных и одежду для будущих мам, получила 1,07 баллов, а покупатель из строки 996, который заказывал только вино, получил 0,15. Таким образом, остаются вопросы:
• насколько регрессия в действительности подходит данным в количественном смысле, а не приблизительно?
• Все это – лишь случайное совпадение или статистически значимый результат?
• Какой вклад вносит каждый отличительный признак в конечный результат?
Чтобы ответить на эти вопросы о линейной регрессии, вам нужно рассчитать R-квадрат, критерий Фишера и критерий Стьюдента для каждого из коэффициентов модели.
R-квадрат – оценка качества подгонки
Если бы вы ничего не знали о покупателе из набора обучающих данных (не было бы столбцов от В до Т), но сделать прогноз о беременности все равно было бы необходимо, то наилучшим способом минимизации квадрата отклонения в таком случае было бы помещение в таблицу среднего значения отклонений в столбце V. Тогда при распределении обучающих данных 500/500 среднее получилось бы равным 0,5. А так как каждое отдельное значение – это либо 0, либо 1, то каждое отклонение будет 0,5, а его квадрат – 0,25. Для 1000 прогнозов эта стратегия прогнозирования среднего дает сумму квадратов, равную 250.
Это значение называется общей суммой квадратов. Это сумма квадратов отклонений каждого значения в столбце V от среднего значения этого столбца. Но Excel предлагает отличную формулу для его расчета в одно действие – DEVSQ/КВАДРОТКЛ.
В ячейке Х2 вы можете рассчитать общую сумму квадратов:
=DEVSQ(V8:V1007)
=КВАДРОТКЛ(V8:V1007)
Но если сложение значений по каждому прогнозу даст нам сумму квадратов отклонений, равную 250, то сумма квадратов отклонений, вычисленная с помощью линейной модели, которую мы недавно подгоняли, гораздо меньше – всего 135,52.
То есть происхождение 135,52 из общей суммы квадратов 250 остается невыясненным, даже после подгонки регрессии (в таком контексте сумма квадратов отклонений часто называется остаточной суммой квадратов).
Если взглянуть на это значение с противоположной стороны, сумма квадратов с выясненным происхождением (которая буквально и является числом, которое мы выяснили с помощью модели) будет равна разнице между 250 и 135,52. Напишите в Х3:
=Х2–Х1
В результате получаем 114,48 – сумму квадратов с выясненным происхождением (если ваша сумма квадратов отклонений отличается от 135,52, то и это значение может немного отличаться).
Насколько хорошее это совпадение?
В целом ответ на этот вопрос можно получить, взглянув на отношение «понятной» суммы квадратов к общей сумме. Это значение называется R-квадрат. Мы можем вычислить его в Х4:
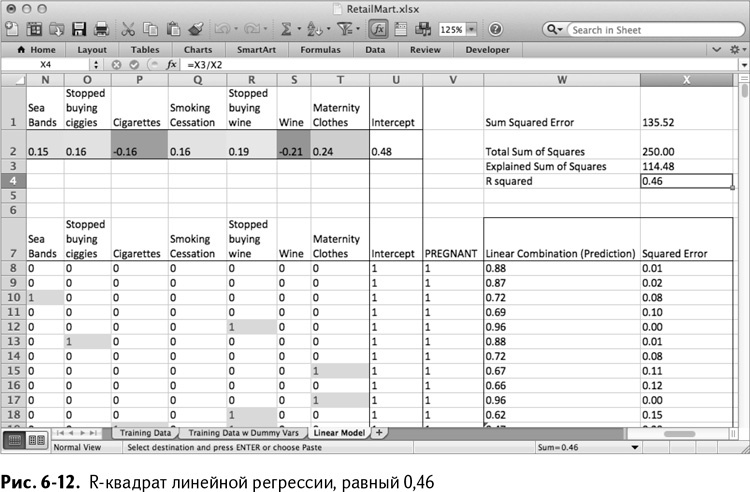
=Х3/Х2
Как показано на рис. 6-12, в результате получается 0,46. Если модель подогнана идеально, то квадрат отклонения будет равен 0, «понятная» сумма квадратов – равняться общей, а R-квадрат будет в точности равен 1. Если модель совсем не подходит, R-квадрат будет ближе к 0. Так что в случае с нашей моделью при таких обучающих вводных данных она может сгодиться для «хорошей, но не идеальной» работы по воспроизведению независимых переменных обучающих данных (столбец Pregnancy).
Не стоит забывать, что расчет R-квадрата работает только для нахождения линейных отношений между данными. Если у вас бешеные нелинейные отношения (возможно, в форме V или U) между зависимыми и независимыми переменными в модели, то R-квадрат не сможет их отобразить.
Критерий Фишера: статистическая значимость подгонки
Частенько при анализе подгонки регрессии люди останавливаются на R-квадрате: «О, неплохо выглядит! Ну все, хватит!»
Не делайте так.
R-квадрат показывает нам лишь то, насколько хорошо подогнана модель. Но он не дает никакой информации о статистической значимости подгонки.
Это просто, особенно в случаях с рассеянными данными (всего несколько точек) – получить модель, которая подогнана достаточно хорошо, но эта подгонка статистически не значима, то есть выраженное ею отношение между отличительными признаками и независимыми переменными может иметь очень отдаленное отношение к реальности.
Может быть, то, что ваша модель подходит – просто случайность? Внезапная удача? Чтобы модель была статистически значимой, нужно отсеять все случайные совпадения. Представим же на мгновение, что вся наша модель – полнейшая случайность. Что вся подгонка – результат удачного выбора из 1000 случайно отобранных анкет РитейлМарта. Такое предположение в стиле адвоката дьявола называется нулевой гипотезой.
Обычно нулевая гипотеза отвергается, если есть вероятность подогнать модель хотя бы на 5 %. Эта вероятность часто называется величиной p.
Для ее вычисления мы проводим проверку на критерий Фишера. Мы берем три параметра модели и создаем с их помощью распределение вероятности (для тех, кто забыл, что такое распределение вероятности – посмотрите обсуждение нормального распределения в главе 4). Вот эти три параметра:
• количество коэффициентов модели – в нашем случае 20 (19 отличительных черт плюс свободный член);
• степени свободы – это количество вариантов данных за вычетом количества коэффициентов модели;
• F-статистика – отношение «понятной» части суммы квадратов к «непонятной» (Х3/Х1 в таблице), умноженное на отношение количества степеней свободы к количеству зависимых переменных.
Чем больше F-статистика, тем ниже вероятность нулевой гипотезы. Как, приняв во внимание описание F-статистики, данное выше, сделать его больше? Увеличьте одно из двух отношений. Вы либо можете «объяснить» больше данных (и таким образом получить лучшую подгонку) или же раздобыть больше данных с таким же количеством переменных (и таким образом убедиться, что ваша подгонка работает и на других данных).
Возвращаясь к таблице: нам нужно подсчитать количество записей и коэффициентов модели.
Назовите ячейку Y1 Observation Count и в Z1 подсчитайте все значения из столбца V:
=COUNT(V8:V1007)
=СЧЁТ(V8:V1007)
Количество записей, как вы и ожидали, равно 1000.
В Z2 подсчитайте количество коэффициентов, суммируя строку 2:
=COUNT(B2:U2)
=СЧЁТ(B2:U2)
У вас должно получиться 20, с учетом свободного члена. Затем в ячейке Z3 вы можете вычислить количество степеней свободы путем вычитания количества коэффициентов модели из количества записей:
=Z1-Z2
У вас получится 980 степеней свободы.
Теперь перейдем к F-статистике в ячейке Z4. Как отмечено выше, это просто отношение «понятной» части суммы квадратов к «непонятной» (Х3/Х1), умноженное на отношение количества степеней свободы к количеству зависимых переменных (Z3/(Z2–1)):
=(X3/X1)*(Z3/(Z2–1))
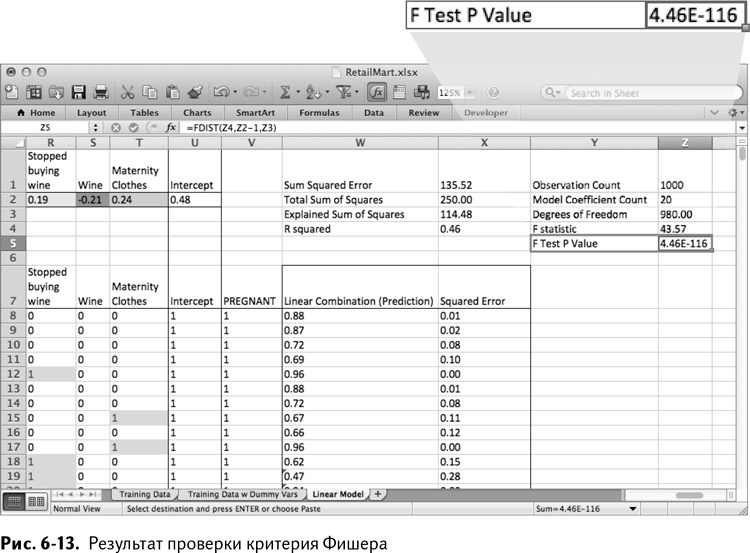
Теперь эти значения можно подставить в распределение Z5 с помощью функции Excel FDIST/FРАСП. Назовите ячейку F Test P Value. Помещаем в FDIST/FРАСП F-статистику, количество зависимых переменных модели и степени свободы:
=FDIST(Z4,Z2–1,Z3)
=FРАСП(Z4,Z2–1,Z3)
Как показано на рис. 6-13, вероятность получения такой подгонки, если принять нулевую гипотезу, почти везде равна нулю. Таким образом, нулевая гипотеза может быть отброшена, а произведенная подгонка – признана статистически значимой.
Проверка коэффициента Стьюдента (Т-тест) – какие переменные являются значимыми?
Осторожно: впереди высшая математика!
Не в пример двум предыдущим проверкам, которые было несложно выполнить, проверка коэффициента Стьюдента для нескольких линейных регрессий потребует от вас перемножения и преобразования матриц. Если вы забыли, как делали это в старших классах школы или на первых курсах института, пролистайте учебник по линейной алгебре или вычислительной математике. Или хотя бы просто Википедию. Воспользуйтесь рабочими таблицами, приложенными к этой книге, чтобы быть уверенным в точности ваших вычислений.В Excel умножение матриц выполняется с помощью функции MMULT/МУМНОЖ, а преобразование – с помощью MINVERSE/МОБР. Так как матрица есть не что иное, как просто прямоугольный массив данных, эти формулы являются формулами массива (подробнее использование формул массива в Excel описано в главе 1).
Если критерий Фишера проверял, насколько значима вся наша регрессия целиком, то есть и способ проверить значимость отдельных переменных. Контролируя значимость каждой отдельной отличительной черты, вы поймете, откуда берутся результаты в вашей модели и от чего они зависят. Статистически незначительные переменные могут быть удалены. Если же вы интуитивно чувствуете, что незначимая переменная должна иметь смысл, то вам стоит проверить чистоту своего набора обучающих данных.
Эта проверка коэффициентов модели называется критерием Стьюдента, или t-тестом. Во время его выполнения, точно так же как и во время проверки критерия Фишера, вы предполагаете, что данный коэффициент модели абсолютно бесполезен и должен быть равен 0. Приняв это предположение, t-тест рассчитывает вероятность получения коэффициента настолько далекого от 0, насколько вы видите в конкретной записи.
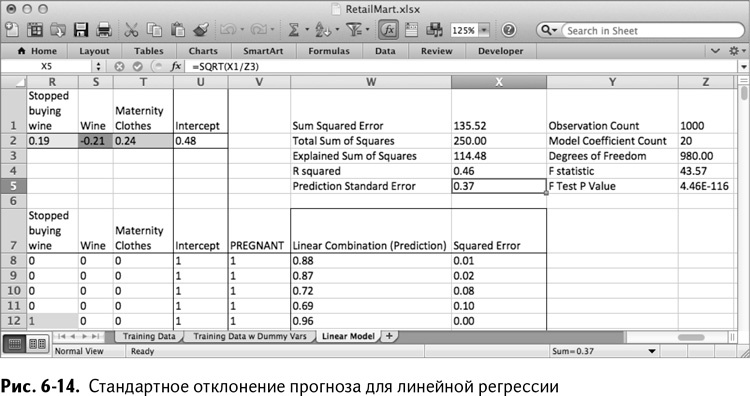
Первое, что вы должны проверить при проведении t-теста зависимой переменной, – это среднеквадратичное отклонение прогноза. Это стандартное распределение выборки отклонения прогноза (более подробно про стандартное распределение рассказывается в главе 4), то есть мера вариабельности отклонений прогноза модели.
Вы можете рассчитать среднеквадратичное отклонение прогноза в ячейке Х5 как квадратный корень из суммы квадрата отклонений (Х1), разделенный на количество степеней свободы (Z3):
=SQRT(X1/Z3)
=КОРЕНЬ(X1/Z3)
Таким образом, мы получаем таблицу, изображенную на рис. 6-14.
С помощью этой величины вы сможете рассчитать стандартное отклонение коэффициента. Подумайте о стандартном отклонении коэффициента как о стандартном распределении этого коэффициента, если вы рисуете каждую отличительную черту как набор данных о тысяче покупателей РитейлМарта, а затем подгоняете ее под отдельную линейную регрессию. Коэффициенты не будут каждый раз одинаковыми, они будут немного отличаться. А стандартное отклонение коэффициента определяет вариабельность, которую вы предполагаете увидеть.
Для расчетов создайте новый лист в рабочей книге и назовите его ModelCoefficientStandardError. Сложным процесс вычисления стандартного отклонения делает необходимость понимать, как обучающие данные для коэффициентов варьируются и сами по себе, и взаимодействуя с другими переменными. Первый шаг в устранении этой неприятности – превращение обучающей последовательности в одну гигантскую матрицу (часто называемую матрицей плана) путем умножения ее на саму себя.
Это произведение матрицы плана и ее же самой (В8:U1007) образует матрицу суммы квадратов и векторных произведений (СКВП). Чтобы увидеть, на что она похожа, вставьте строку заголовков обучающих данных в лист ModelCoefficientStdError в В1:U1 и, транспонированную, в А2:А21, вместе с заголовком Intercept.
Чтобы умножить матрицу плана на саму себя, нужно обработать ее функцией Excel MMULT/МУМНОЖ, сначала транспонированную, затем правой стороной вверх:
{=MMULT(TRANSPOSE(‘Linear Model’!B8:U1007),’Linear Model’! B8:U1007)}
{=МУМНОЖ(ТРАНСП(‘Linear Model’!B8:U1007),’Linear Model’! B8:U1007)}
Так как эта формула выдает результат в виде матрицы, переменную за переменной, вам нужно выделить весь промежуток В2:U21 на листе ModelCoefficientStdError и использовать формулу как формулу массива (о формулах массива более подробно говорится в главе 1).
У вас получается таблица, изображенная на рис. 6-15.
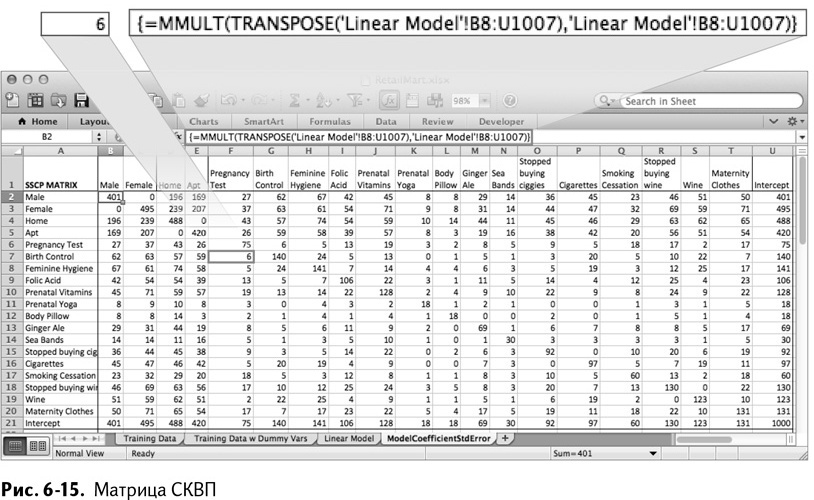
Обратите внимание на значения в матрице СКВП. По диагонали вы считаете совпадения каждой переменной с самой собой – то же, что и простое сложение единиц из каждого столбца матрицы плана. Свободный член получается равным 1000 в ячейке, к примеру, U21, потому что в исходных обучающих данных этот столбец состоит из 1000 ячеек.
В ячейках, не входящих в диагональ, вас интересует число совпадений разных признаков. И если «мужчина» и «женщина» точно ни у кого не попадутся одновременно, то тест на беременность и противозачаточные появляются вместе в шести покупательских строках наших данных.
Матрица СКВП дает нам представление о величине каждой переменной и то, насколько они пересекаются и соотносятся между собой.
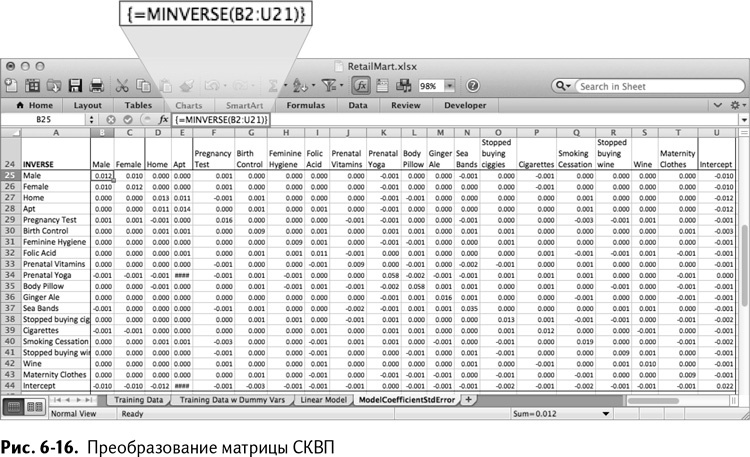
Вычисление стандартного отклонения коэффициента требует преобразования матрицы СКВП. Для его выполнения вставьте заголовки еще раз под саму матрицу в В24:U24 и А25:А44. Преобразование матрицы в В2:U21 рассчитывается выделением В25:U44 и применением функции MINVERSE/МОБР как формулы массива:
{=MINVERSE(B2:U21)}
{=МОБР(B2:U21)}
Таким образом мы получаем таблицу, как на рис. 6-16.
Значения, требуемые для вычисления стандартного отклонения коэффициента, находятся в диагонали преобразованной матрицы СКВП. Каждое из них рассчитывается как стандартное отклонение прогноза для целой модели (как до этого мы получили 0,37 в ячейке Х5 листа Linear Model), которое зависит от квадратного корня из соответствующего значения из диагонали СКВП.
Например, стандартное отклонение коэффициента для параметра Male (мужчина) будет равным квадратному корню из значения совпадения его с самим собой в преобразованной матрице СКВП (корню из 0,0122), умноженному на стандартное отклонение прогноза.
Чтобы рассчитать его для всех переменных, пронумеруйте каждую из них, начиная с 1 в В46 и заканчивая 20 в U46. Соответствующее каждому отличию диагональное значение затем можно найти с помощью формулы INDEX/ИНДЕКС. К примеру, INDEX(ModelCoefficientStdError!B25
:B44,ModelCoefficientStdError!B46)
/ИНДЕКС(ModelCoefficientStdError!B25
:B44,ModelCoefficientStdError!B46)
выдает значение пересечения строки Male со столбцом Male (подробнее о формуле INDEX/ИНДЕКС прочитайте в главе 1).
Извлекая из этого значения квадратный корень, а затем умножая его на стандартное отклонение прогноза, можно рассчитать стандартное отклонение коэффициента Male в ячейке В47:
=’LinearModel’!$X5×SQRT(INDEX(ModelCoefficientStdError!
B25:B44,ModelCoefficientStdError!B46))
=’LinearModel’!$X5×КОРЕНЬ(ИНДЕКС(ModelCoefficientStdError!
B25:B44,ModelCoefficientStdError!B46))
Для модели, подогнанной в этой книге, результат равен 0,04.
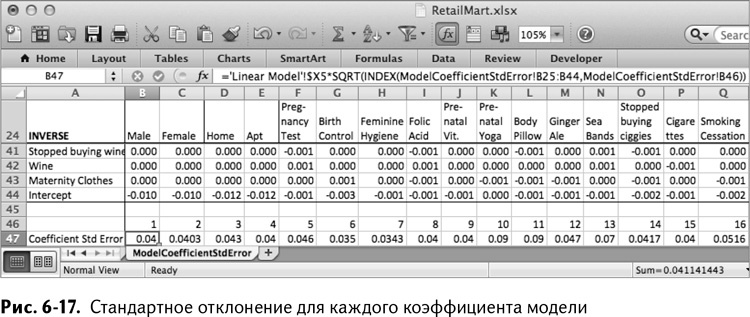
Растяните эту формулу до столбца U, чтобы получить стандартные отклонения всех коэффициентов, как показано на рис. 6-17.
На листе Linear Model поместите в ячейку А3 заголовок Coefficient Standard Error. Скопируйте стандартные отклонения коэффициентов и вставьте их значения в строку 3 этого листа.
Фух! С этого момента станет легче. До самого конца книги больше ни одного вычисления с матрицами. Клянусь!
Теперь у вас есть все, что нужно для подсчета статистики каждого коэффициента (такого же, как и расчет F-статистики в предыдущем разделе). Мы будем производить проверку по двустороннему критерию, то есть рассчитывать вероятности получения коэффициента, по меньшей мере, такой же величины, положительной или отрицательной, если на самом деле между отличием и зависимой переменной нет никакой связи.
T-статистика для этой проверки может быть рассчитана в строке 4 как абсолютное значение коэффициента, нормализированного по его стандартному отклонению. Для признака Male это будет выглядеть так:
=ABS(B2/B3)
Раскопируйте эту формулу по всем ячейкам столбца U, относящимся к переменным.
Проверку критерия Стьюдента теперь можно дополнить оценкой распределения Стьюдента (еще одного статистического распределения, вроде нормального распределения из главы 4) относительно значения t-статистики (статистики Стьюдента) для ваших значений степеней свободы. Озаглавьте строку 5 t Test p Value, а в В5 поместите формулу TDIST/СТЬЮДРАСП для расчета вероятности того, что коэффициент будет по меньшей мере таким, как при нулевой гипотезе:
=TDIST(B4,$Z3,2)
=СТЬЮДРАСП(B4,$Z3,2)
Двойка в этой формуле обозначает двусторонний критерий. Копируя эту формулу на все переменные и применяя условное форматирование для ячеек, содержащих значения не меньше 0,05 (пятипроцентная вероятность), вы увидите, какие отличительные черты статистически не значимы. Ваши результаты могут отличаться из-за разницы в подгонке модели, а в таблице, показанной на рис. 6-18, столбцы Female, Home и Apt представлены как статистически не значимые.
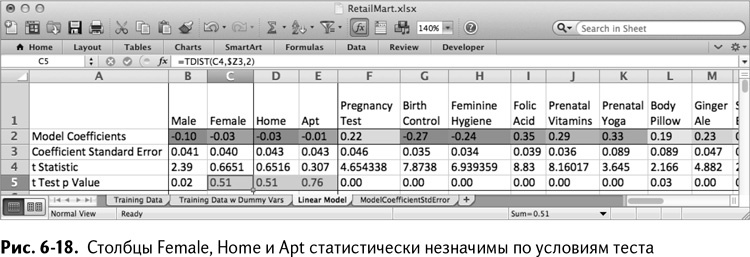
Для обучения модели в дальнейшем эти столбцы нужно будет удалить.
Теперь, когда вы научились оценивать модель по статистическим критериям, сменим подход и обратимся к измерению качества модели, делая прогнозы на основании набора данных.
Делаем прогнозы на основании новых данных и измеряем результат
Последний раздел был целиком посвящен статистике – своего рода лабораторная работа. Это, конечно, не самое веселое, что вы делали в своей жизни, но умение проверять значимость и качество подгонки – важные навыки. А теперь пришло время устроить полевые испытания нашей модели и повеселиться!
Как вы узнаете, что ваша линейная модель хорошо справляется с прогнозированием реальных вещей? В конце концов, ваш обучающий набор данных не содержит все возможные записи о покупателях, а ваши коэффициенты были специально подогнаны под модель (хотя если вы сделали все правильно, обучающие данные довольно верно описывают картину мира).
Чтобы лучше понять, как модель будет себя вести в реальном мире, нужно пропустить через нее несколько покупателей, которые не участвовали в предыдущем ее обучении. Этот отдельный набор примеров, используемый для тестирования модели, часто называется контрольной, или тестовой, выборкой, либо тестовой последовательностью.
Чтобы обзавестись такой выборкой, нужно просто вернуться к базе данных РитейлМарта и выбрать других случайных покупателей (стараясь не наткнуться на тех, кто уже был выбран для обучения). Теперь, как отмечалось ранее, 6 % покупателей РитейлМарта беременны, поэтому если вы выбрали 1000 случайных покупателей из базы, то примерно 60 из них окажутся беременными.
Если для обучения модели вы делали выборку с запасом, то для тестирования стоит оставить отношение семей, ждущих ребенка, к остальным на уровне тех же 6 %, чтобы измерения точности модели соответствовали тому, как модель будет себя вести в реальных условиях.
В электронной таблице, соответствующей этой главе (доступна к загрузке на сайте книги), вы найдете вкладку под названием Training Set, заполненную тысячей строк с данными, подобно обучающему набору. Первые 60 покупателей беременны, а 940 остальных – нет (рис. 6-19).
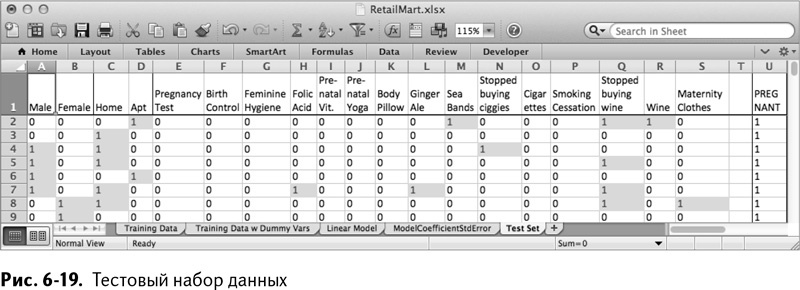
Точно так же, как во вкладке Linear Model, пропустите этот набор через модель, подставляя новые данные в линейную комбинацию данных покупателей и коэффициентов, и затем прибавляя свободный член.
Помещая этот прогноз в столбец V, в строке 2 вы получаете следующую формулу для первого покупателя (так как в тестовом наборе нет столбца со свободным членом, следует добавить его отдельно):
=SUMPRODUCT(‘LinearModel’!B$2:T$2,’TestSet’!A2:S2)+
’LinearModel’!U$2
=СУММПРОИЗВ(‘LinearModel’!B$2:T$2,’TestSet’!A2:S2)+
’LinearModel’!U$2
Скопируйте этот расчет для всех покупателей. Таблица, которая получается в итоге, изображена на рис. 6-20.
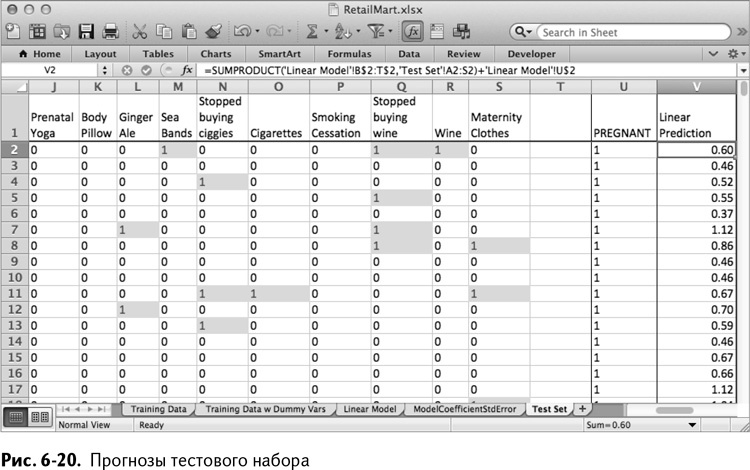
На рис. 6-20 вы видите, что модель идентифицировала много семей, ожидающих прибавления, с прогнозами ближе к 1, чем к 0. Самые высокие значения прогноза получены для семей, которые покупали товары, четко относящиеся к беременности – фолиевую кислоту или витамины для беременных.
С другой стороны, среди этих 60 «беременных» семей есть такие, которые не покупали ничего указывавшего на беременность. Конечно, они не покупали алкоголь или табак, но, как показывают их более низкие прогнозы, отсутствие покупки немного значит.
И наоборот, посмотрев на прогнозы «не-беременных» семей, вы увидите несколько упущений. К примеру, если вы следите за мной по таблице, то в строке 154 «не-беременный» покупатель заказывает одежду для беременных и перестает заказывать сигареты, а модель дает ему прогноз в 0,76.
Таким образом, становится ясно, что если вы действительно собираетесь использовать эти прогнозы в собственном маркетинге, то вам придется установить некий порог для того, чтобы счесть покупателя беременным и начать отправлять ему соответствующие предложения. Возможно, нужно посылать рекламные материалы всем, у кого прогноз 0,8 и больше. Но, может быть, для вящей уверенности стоит поднять порог до 0,95.
Перед тем как установить этот порог классификации, посмотрите на баланс плюсов и минусов в оценке качества работы модели. Измерения, больше всего влияющие на этот показатель, основаны на количествах и отношениях четырех величин, получаемых из нашей тестовой выборки:
• действительно положительные – отнесение беременного покупателя к беременным;
• действительно отрицательные – отнесение «не-беременного» покупателя к не беременным;
• ложноположительные (также называемые ошибками I рода) – отнесение «не очень беременного» покупателя к беременным. По моему опыту, конкретно это ложноположительное предположение очень обижает при личном контакте;
• ложноположительные (также называемые ошибками II рода) – неспособность определить беременного покупателя как такового. Это не так обидно, как подсказывает мой опыт.
Несмотря на большое количество различных измерений качества работы модели, они все похожи на мексиканскую кухню – фактически являясь комбинацией одних и тех же четырех ингредиентов, перечисленных выше.
Установка граничных значений
Создайте новый лист и назовите его Performance. Самое меньшее значение, которое можно использовать в качестве граничного между беременными и не беременными, – это значение наименьшего прогноза в тестовой выборке. Назовите ячейку А1 Min Prediction, а в А2 поместите расчет:
=MIN(‘TestSet’!V2:V1001)
=МИН(‘Test Set’!V2:V1001)
Аналогично, максимальной величиной может стать максимальное значение прогноза по тестовой выборке. Назовите А4 Max Prediction, а в А5 поместите формулу расчета:
=MAX(‘Test Set’!V2:V1001)
=МАКС(‘Test Set’!V2:V1001)
Значения, описанные выше, составляют –0,35 и 1,25, соответственно. Не забывайте, что ваша линейная регрессия способна делать предположения и ниже 0, и выше 1, потому что на самом деле это не вероятности попадания в определенный класс (ими мы займемся позже в другой модели).
Добавьте в столбец В заголовок Probability Cutoff for Pregnant Classification, а под ним определите промежуток его значений, начинающийся с –0,35. На листе, показанном на рис. 6-21, граничные значения меняются в большую сторону с шагом 0,05 до самого максимума 1,25 (просто введите первые три значения вручную, затем выделите их и растяните вниз, чтобы заполнить столбец до конца).
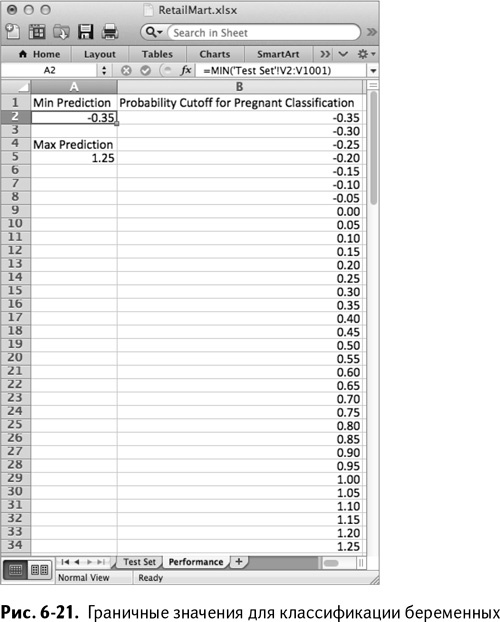
Особо дотошные могут считать граничным значение каждого прогноза в тестовой последовательности.
Точность (положительная прогностическая ценность)
А теперь давайте заполним некоторые параметры качества модели для каждого из этих граничных значений с помощью прогнозов по тестовой последовательности, начиная с точности, также известной как положительная прогностическая ценность полученного результата.
Точность – это мера того, сколько семей в ожидании детей мы определили верно из всех семей, которые модель назвала «беременными». Говоря деловым языком, точность – это процент той рыбы в ваших сетях, которая является тунцом, а не дельфинами.
Назовите столбец С Precision. Допустим, граничное значение находится в В2 и равно –0,35. Какова точность нашей модели, если беременным мы считаем каждого с прогнозом –0,35 и выше?
Для расчета вернитесь к листу Test Set и сосчитайте количество случаев, когда «беременная» семья получала прогноз больше или равный –0,35, а затем разделите это количество на общее число строк с прогнозом –0,35 и выше. Используйте формулу COUNTIFS/СЧЁТЕСЛИМН для проверки действительно беременных и предполагаемых, которая в ячейке С2 будет выглядеть так:
=COUNTIFS(‘TestSet’!$V$2:$V$1001,”>=”&B2,‘TestSet’!$U$2:
$U$1001,”=1”)/COUNTIF(‘TestSet’!$V$2:$V$1001,”>=”&B2)
=СЧЁТЕСЛИМН(‘TestSet’!$V$2:$V$1001,”>=”&B2,‘TestSet’!$U$2:
$U$1001,”=1”)/СЧЁТЕСЛИ(‘TestSet’!$V$2:$V$1001,”>=”&B2)
Первый оператор COUNTIFS/СЧЁТЕСЛИМН в формуле сравнивает и действительную беременность, и прогноз модели, в то время как COUNTIF/СЧЁТЕСЛИ в знаменателе считает только тех, чей прогноз выше –0,35, независимо от беременности. Вы можете растянуть эту формулу на все пороговые значения.
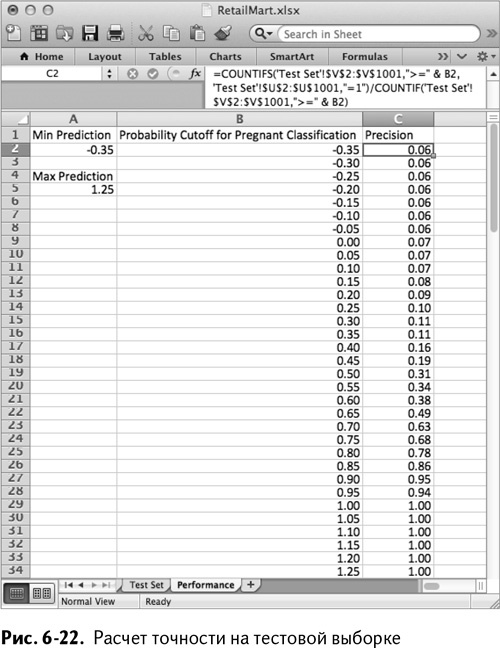
Как показано на рис. 6-22, точность модели возрастает с увеличением граничного значения, а при границе, равной 1, модель становится идеально точной. Идеально точная модель считает беременными только беременных покупателей.
Избирательность (доля действительно отрицательных результатов)
Еще одна мера качества модели, которая растет вместе с пороговым значением, – это избирательность. Избирательность, также называемая долей действительно отрицательных результатов, выражается количеством покупателей, которые были верно отнесены к таковым (действительно отрицательный результат), разделенным на общее количество «не-беременных» семей.
Озаглавив столбец D Specificity/True Negative Rate, в D2 вы можете вычислить это значение с помощью формулы COUNTIFS/СЧЁТЕСЛИМН в числителе, чтобы узнать количество действительно «не-беременных», и COUNTIF/СЧЁТЕСЛИ в знаменателе, чтобы подсчитать всех «не-беременных» покупателей:
=COUNTIFS(‘TestSet’!$V$2:$V$1001,”<”&B2,‘TestSet’!$U$2:
$U$1001,”=0”)/COUNTIF(‘TestSet’!$U$2:$U$1001,”=0”)
=СЧЁТЕСЛИМН(‘TestSet’!$V$2:$V$1001,”<”&B2,‘TestSet’!$U$2:
$U$1001,”=0”)/СЧЁТЕСЛИ(‘TestSet’!$U$2:$U$1001,”=0”)
Копируя эти вычисления на все строки с граничными значениями, можно увидеть, что значение его возрастает (рис. 6-23). По достижении граничного значения 0,85 правильно определяется 100 % «не-беременных» покупателей.
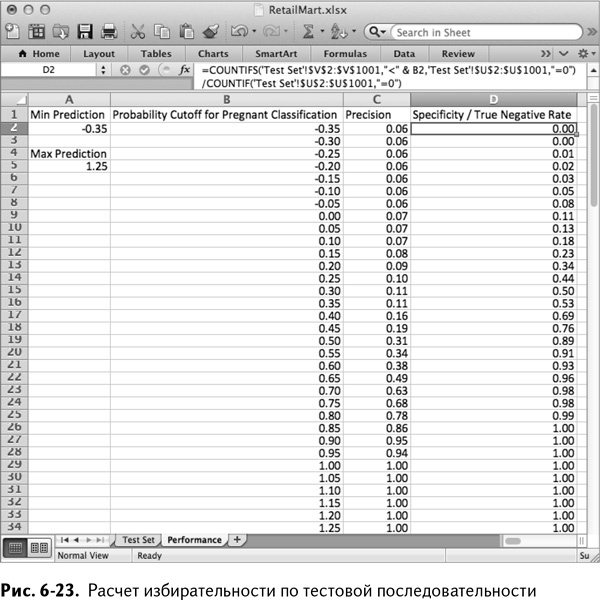
Доля ложноположительных результатов
Доля ложноположительных результатов – это стандартный параметр, по которому определяется качество модели. А так как у вас уже есть доля действительно отрицательных результатов, то он может быть быстро вычислен как разница между единицей и этой величиной. Назовите столбец Е False Positive Rate/(1 – Specificity) и заполните ячейки этой разницей между единицей и значением соответствующей ячейки столбца D. В Е2 это будет выглядеть так:
=1-D2
Копируя эту формулу на весь список, вы можете увидеть, что по мере возрастания граничного значения, уменьшается количество ложноположительных результатов. Другими словами, вы совершаете меньше ошибок I рода (называя беременными покупателей, которые таковыми не являются).
Доля действительно положительных результатов /
память / чувствительность
Последний параметр качества модели, который вы можете рассчитать, называется долей действительно положительных значений. И памятью. И чувствительностью. Ох, зачем придумывать столько названий для одного и того же!
Доля действительно положительных значений – это количество правильно определенных беременных женщин, разделенное на общее количестве таковых в тестовом наборе. Назовите столбец F True Positive Rate/Recall/Sensitivity. В ячейке F2 теперь можно вычислить долю действительно положительных значений при граничной величине, равной –0,35:
=COUNTIFS(‘TestSet’!$V$2:$V$1001,”>=”&B2,‘TestSet’!$U$2:
$U$1001,”=1”)/COUNTIF(‘TestSet’!$U$2:$U$1001,”=1”)
=СЧЁТЕСЛИМН(‘TestSet’!$V$2:$V$1001,”>=”&B2,‘TestSet’!$U$2:
$U$1001,”=1”)/СЧЁТЕСЛИ(‘TestSet’!$U$2:$U$1001,”=1”)
Возвращаясь к столбцу с действительно отрицательными результатами, отмечу, что вычисления здесь практически идентичны, за исключением того, что «<» превращается в «≥», а нули становятся единицами.
Копируя эту формулу на весь столбец, вы можете убедиться, что с ростом граничного значения некоторые беременные женщины перестают определяться как таковые (ошибка II рода), а доля действительно положительных значений падает. На рис. 6-24 показаны доли действительных и ложноположительных значений в столбцах E и F.
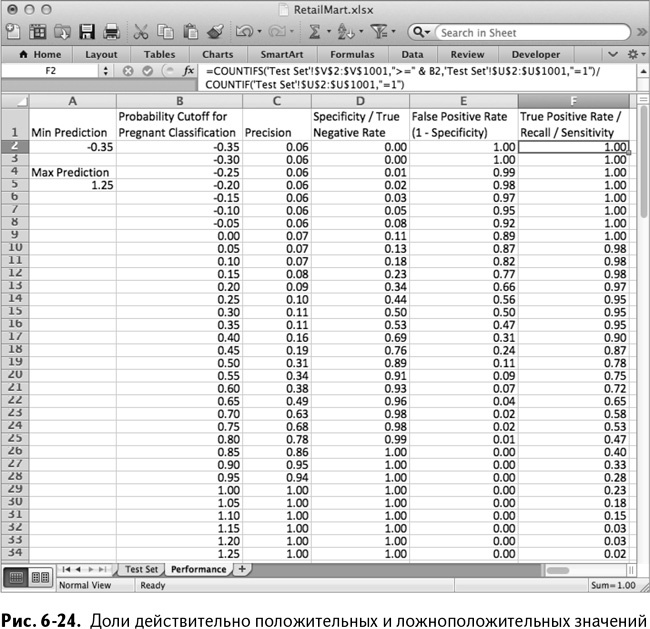
Оценка соотношения измерений и кривая ошибок
При выборе порогового значения для бинарного классификатора важно выбрать наилучший баланс параметров качества его работы. Чем выше порог, тем выше точность модели, но ниже выборка. Одна из наиболее популярных визуализаций, которые используются для просмотра этой оценки, – это кривая ошибок (кривая соотношений правильного и ложного обнаружения сигналов, или рабочей характеристики приемника – Receiver Operating Characteristic, ROC). Кривая ошибок – это просто график зависимости действительно положительных значений от ложноположительных (столбцы E и F на листе Performance).
ПРИ ЧЕМ ТУТ «РАБОЧАЯ ХАРАКТЕРИСТИКА ПРИЕМНИКА»?
Причина, по которой такой простой график называется так сложно, проста: он был разработан радиотехниками во время Второй мировой войны, а не маркетологами на прошлой неделе для определения беременных покупателей.Эти ребята использовали сигналы для обнаружения врага и вражеской техники на поле боя и хотели визуально отобразить соотношение между верно и неверно определяемыми целями.
Для того чтобы вставить график, выделите данные в столбцах E и F и выберите в меню диаграмм Excel «линейную диаграмму» (технология вставки графиков и диаграмм более подробно описана в главе 1). После небольшого форматирования (установки значений по осям от 0 до 1 и выбора удобного шрифта) кривая ошибок выглядит так, как показано на рис. 6-25.
Эта кривая позволяет вам быстро увидеть долю ложноположительных значений, соотнесенную с долей действительно положительных, и лучше их понять. К примеру, на рис. 6-25 можно увидеть, что модель способна идентифицировать 40 % беременных покупателей при пороговом значении 0,85 без единого «ложного срабатывания». Неплохо!
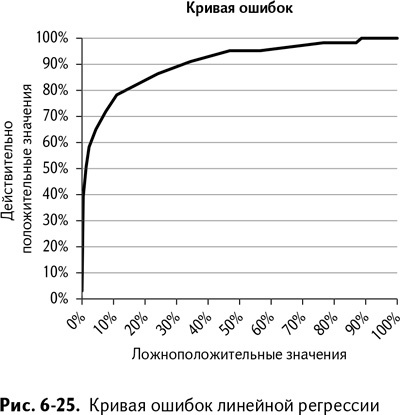
А если вас устраивает редкая отсылка семьям, не ожидающим детей, купонов, связанных с беременностью, модель может достичь доли действительно положительных значений в 75 % при всего лишь 9 «ложных срабатываниях».
То, какое значение вы установите в качестве порогового для определения «баллов беременности» покупателей – это бизнес-решение, а не чистая аналитика. Конечно, вместе с небольшим понижением порога определения беременности понизится и точность, но это весьма малая жертва, если принять во внимание существенное повышение доли действительно положительных значений. А при прогнозировании не беременности, а дефолта облигаций займа, вам наверняка захочется, чтобы специфичность и точность были немного повыше, не правда ли? И если бы модель, подобная этой, использовалась для подтверждения степени реальности военной угрозы, вы бы наверняка надеялись, что оператор модели пользовался очень высокой степенью точности перед тем, как вызвать беспилотники для атаки.
СРАВНЕНИЕ ОДНОЙ МОДЕЛИ С ДРУГОЙ
Как мы убедимся немного ниже, кривая ошибок также подходит для выбора между двумя прогностическими моделями. В идеале эта кривая подскакивает до 1 по оси у с максимально возможной скоростью и остается там до конца графика. Так что модель, график которой более похож на описанный выше (также стоит отметить, что она должна иметь наибольшую площадь под кривой), часто считается лучшей.
Так что о чем бы мы ни говорили – об отправке купонов, одобрении кредита или объявлении готовности № 1, – решение о выборе баланса между параметрами качества является стратегическим.
Отлично! Мы опробовали модель на тестовых данных, сделали несколько прогнозов, рассчитали ее качественные показатели на тестовом наборе данных для различных граничных значений и отобразили эти показатели на кривой ошибок.
Но чтобы с чем-то сравнить качество модели, нужна еще одна.
Назад: Не обольщайтесь!
Дальше: Предсказание беременных покупателей РитейлМарта с помощью логистической регрессии

