Предсказание беременных покупателей РитейлМарта с помощью логистической регрессии

Книга: Много цифр. Анализ больших данных при помощи Excel

Назад: Определение беременных покупателей РитейлМарта с помощью линейной регрессии

Если взглянуть на предсказанные нашей линейной регрессией значения, становится ясно: модель полезна для классификации, но сами прогностические значения, конечно, не являются вероятностями класса. Вы не можете быть беременны со 125 %-ной или 35 %-ной вероятностью.

Так существует ли модель, чьи прогнозы, и правда, были бы вероятностями класса?

Мы можем создать такую модель, и называется она логистической регрессией.

Первое, что нам нужно – это функция связи

Подумайте о прогнозах, которые выдает ваша модель. Существует ли такая формула, через которую можно пропустить эти цифры, чтобы они оставались между 0 и 1? Оказывается, такая функция называется функцией связи, и есть отличный ее вариант, который делает очень простую операцию:

exp(x)/(1+exp(x))

В этой формуле х – линейная комбинация значений из столбца W вкладки Linear Model и функции экспоненты, выраженной сокращенно exp. Экспонента exp(x), иначе называемая числом е, – просто математическая константа, равная 2,71828 – это что-то вроде «числа пи», только поменьше, в нашей формуле возведенная в степень х.

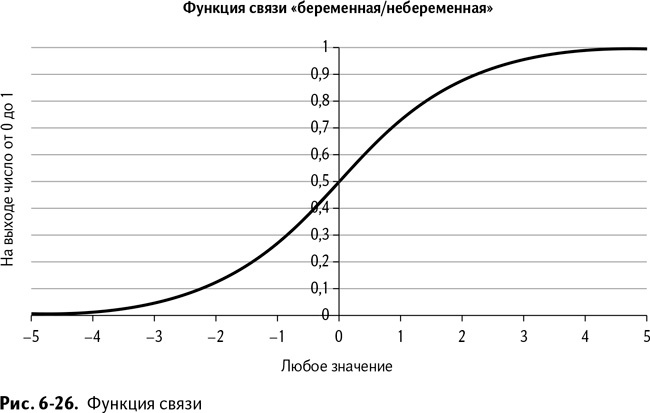
Посмотрите на график этой функции, изображенный на рис. 6-26.

Эта функция связи похожа на растянутую S. В нее можно подставить любое значение, полученное умножением коэффициентов модели на значение из строки данных покупателя, и на выходе получить число от 0 до 1. Но почему эта странная функция так выглядит?

А вы попробуйте быстренько округлить е до 2,7 и представьте ситуацию, когда вводные данные действительно велики, скажем х = 10. Тогда функция связи будет выглядеть следующим образом:

exp(x)/(1+exp(x))=2,7^10/(1+2,7^10)=20589/20590

Это же практически 1, и с увеличением х эта единица в знаменателе значит все меньше и меньше. А как насчет отрицательного х?

Посмотрите на –10:

exp(x)/(1+exp(x))=2,7^-10/(1+2,7^-10)=0,00005/1,00005

По большому счету, это 0. Так что в данном случае 1 в знаменателе играет очень даже существенную роль, а небольшие величины так или иначе близки к 0. Полезно ли это? На деле эта функция связи оказалась настолько полезной, что кто-то дал ей собственное название. Это «логистическая» функция.

Присоединение логистической функции и реоптимизация

Пришло время снова скопировать лист, в этот раз – Linear Model, и назвать копию Logistic Link Model. Удалите все статистические тестовые данные, так как они относились к линейной регрессии. Отдельно выделите и удалите строки с 3 по 5, а также все значения вверху строк от W до Z, кроме названия Sum Squared Error. Также очистите столбец с квадратом отклонения и назовите его Prediction (after Link Function). На рис. 6-27 показано, как должен выглядеть этот лист в итоге.

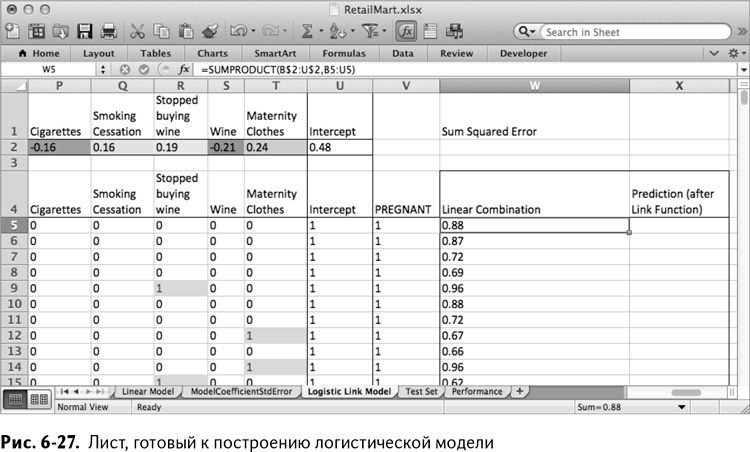
Столбец Х вы будете использовать для получения результата из вашей логистической функции путем пропускания через нее линейной комбинации коэффициентов и данных из столбца W. К примеру, первая строка смоделированных данных покупателей будет обработана формулой в ячейке Х5:

=EXP(W5)/(1+EXP(W5))

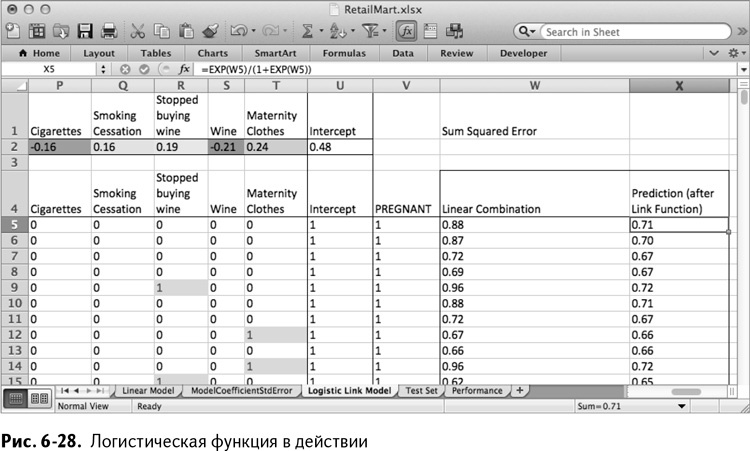
Если скопировать эту формулу на весь столбец, можно увидеть, что все новые значения находятся между 0 и 1 (рис. 6-28).

Так или иначе, большая часть прогнозов оказывается близка к среднему, между 0,4 и 0,7. А все из-за того, что мы не оптимизировали коэффициенты на листе Linear Model для нашей новой модели. Так что оптимизацию придется повторить.

Поэтому мы снова заполняем столбец с квадратом отклонения и далее столбцы до Y, но теперь в расчет отклонения включаем прогнозы линейной функции из столбца Х:

=(V5-X5)^2

Их мы снова складываем, точно так же, как в ячейке Х1 линейной модели:

=SUM(Y5:Y1004)

Заметка

Ваши значения в столбцах W и X могут немного отличаться от моих, так как это – коэффициенты модели, которые мы искали с помощью эволюционного алгоритма на предыдущем листе.

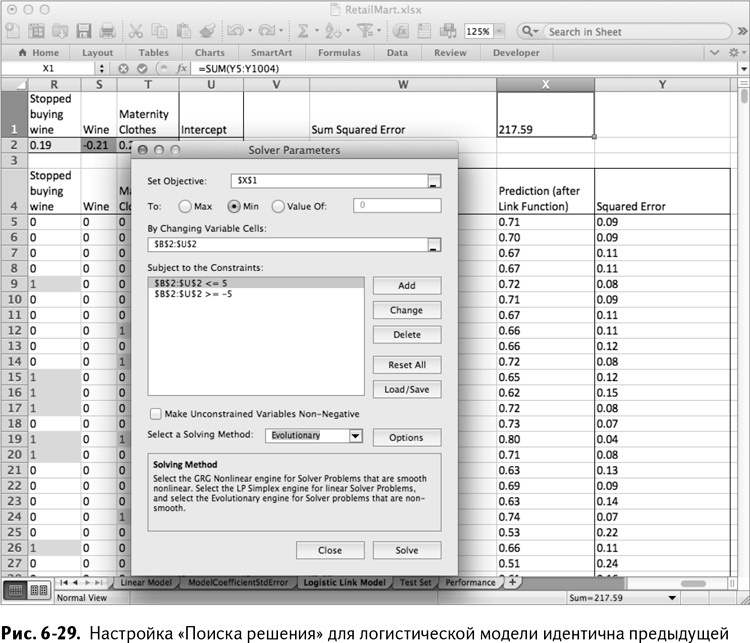
Затем минимизируем сумму квадратов этой новой модели, пользуясь «Поиском решения», настроенным точно так же, как в прошлый раз (рис. 6-29), с единственным отличием: если вы экспериментируете с различными границами, то лучший вариант из возможных – это немного их расширить для логистической модели. На рис. 6-29 границы установлены таким образом, чтобы коэффициенты находились между –5 и 5.

Закончив с реоптимизацией для новой функции связи, вы можете заметить, что теперь все ваши прогнозы по обучающим данным находятся между 0 и 1, причем многие из них с уверенностью можно отнести к 1 или 0. Как вы видите на рис. 6-30, эстетически такие прогнозы выглядят лучше, чем результаты линейной регрессии.

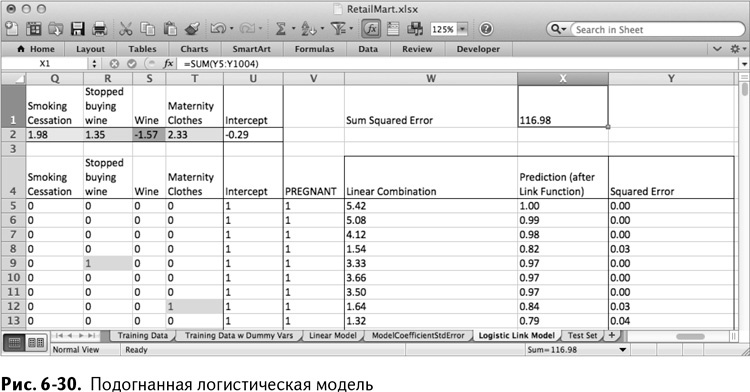
Создание настоящей логистической регрессии

Правда состоит в том, что для создания настоящей логистической регрессии, дающей точные, беспристрастные свойства классов, вы не можете минимизировать сумму квадрата отклонения по причинам, находящимся за пределами охвата этой книги.

Вместо этого подгонка модели заключается в нахождении коэффициентов, максимизирующих совместную вероятность (подробнее о ней можно прочитать в главе 3) извлечения этой обучающей выборки из базы данных РитейлМарта при том, что модель точно описывает реальность.

Так какова же вероятность строки обучающих данных при известном наборе параметров логистической модели? Для данной строки в обучающем наборе пусть р выражает классовую вероятность, которую ваша логистическая модель выдает в столбце Х. А у пусть выражает значение действительной беременности, располагающееся в столбце V. Вероятность такой обучающей строки при данных параметрах модели будет равна

py(1-p)(1–y)

Для беременного покупателя (1 в столбце V) с прогнозом, равным 1 (1 в столбце Х), вычисление такой вероятности также дает 1. Но если прогноз у беременного покупателя был равен 0, то результатом этого вычисления будет уже 0 (подставьте значения и проверьте). Таким образом, вероятность каждой строки максимальна, когда предположение и реальность сходятся.

Принимая независимость каждой строки данных (более подробно понятие независимости описано в главе 3), как в случае любой хорошей случайной выборки из базы данных, можно вычислить логарифм совместной вероятности данных, логарифмируя каждую из этих вероятностей и затем складывая их. Логарифм уравнения, приведенного выше, вычисленный с помощью тех же правил, что вы видели в разделе главы 3 о плавающей запятой, будет равен:

Y*ln(p)+(1-y)*ln(1-p)

Вероятность логарифма близка к 0, если результат предыдущей формулы был близок к 1 (то есть когда модель хорошо подогнана).

Вместо того, чтобы минимизировать сумму квадрата отклонения, вы можете вычислить значение логарифмической функции правдоподобия для каждого прогноза, и затем сложить их. Те коэффициенты модели, которые максимизируют совместную вероятность, будут наилучшими.

Для начала сделайте копию листа Logistic Link Model и назовите ее Logistic Regression. В столбце Y замените название Squared Error (квадрат отклонения) на Log Likelihood (логарифмическое правдоподобие). В ячейке Y5 первое значение этой величины будет вычисляться по формуле:

=IFERROR(V5*LN(X5)+(1-V5)*LN(1-X5),0)

=ЕСЛИОШИБКА(V5*LN(X5)+(1-V5)*LN(1-X5),0)

Полное вычисление логарифмического правдоподобия заключается в единственной формуле – IFERROR/ЕСЛИОШИБКА, ведь когда коэффициенты модели генерируют прогноз, очень-очень близкий к действительному значению класса 0/1, вы можете получить неустойчивость численного решения. В таком случае вполне справедливо установить значение логарифмического правдоподобия на 0 – идеальное сходство.

Статистические тесты логистической регрессии

Статистические критерии, аналогичные r-квадрату и критериям Фишера, и Стьюдента, существуют и для логистической регрессии. Такие вычисления как псевдо-r-квадрат, отклонение модели и тест Вальда дают логистической регрессии практически ту же точность, что и у линейной регрессии. Более подробно об этом можно прочитать в книге «AppliedLogisticRegression», David W. Hosmer, Jr., Stanley Lemeshow, and Rodney X. Sturdivant (John Wiley & Sons, 2013).

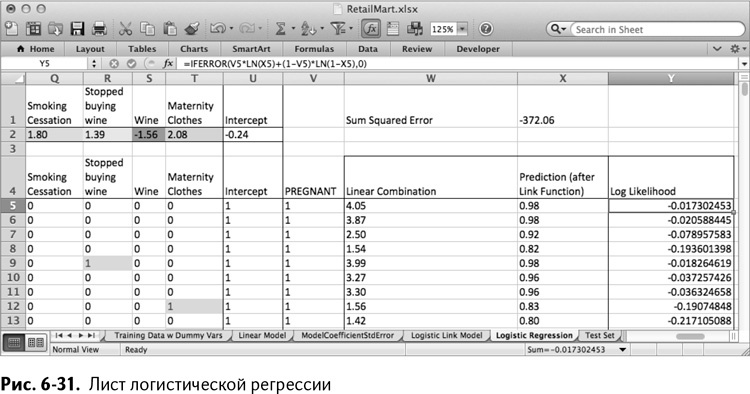
Скопируйте эту формулу на весь столбец Y, а в Х1 подсчитайте сумму значений логарифмического правдоподобия. Оптимизируя, вы получаете набор коэффициентов, очень похожий на найденный с помощью суммы квадратов отклонений, с небольшими расхождениями тут и там (рис. 6-31).

При проверке сумма квадратов отклонений для полученной логистической регрессии должна оказаться практически оптимальной для такого параметра.

Выбор модели: сравнение работы линейной и логистической регрессий

Теперь, когда у вас есть вторая модель, можно приступить к сравнению ее работы с работой линейной регрессии с помощью тестовых данных. Логистическая регрессия делает свои предположения как и написано в столбцах W и Х листа Logistic Regression.

В ячейке W2 листа Test Set вычислите значение линейной комбинации коэффициентов модели и тестовых данных следующим образом:

=SUMPRODUCT(‘LogisticRegression’!B$2:T$2,’TestSet’!A2:S2)+

‘LogisticRegression’!U$2

=СУММПРОИЗВ(‘LogisticRegression’!B$2:T$2,’TestSet’!A2:S2)+

‘LogisticRegression’!U$2

В ячейке Х2 подставьте это значение в функцию связи, чтобы получить классовую вероятность:

=EXP(W2)/(1+EXP(W2))

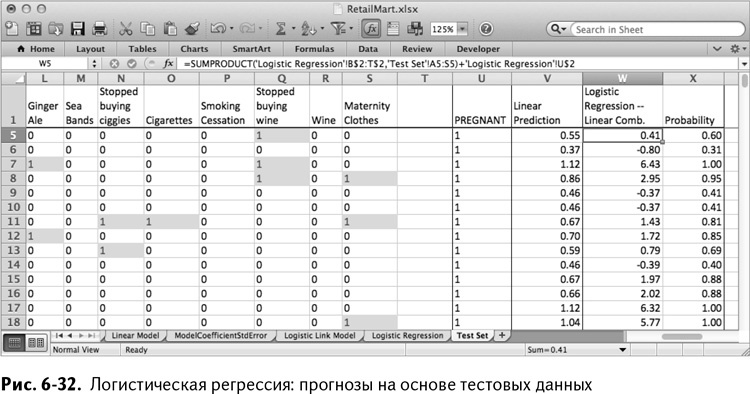
Скопировав эти формулы на оба столбца листа тестовых данных, вы получите лист, изображенный на рис. 6-32.

Чтобы увидеть, как располагаются прогнозы, скопируйте лист Performance и назовите его Performance Logistic. После изменения формул максимального и минимального прогнозов таким образом, чтобы они обращались к столбцу Х, значения остаются в промежутке между 0 и 1, как вы и хотели, и модель, в отличие от линейной регрессии, теперь выдает текущие значения вероятностей принадлежности к классам.

Заметка

Результатом работы логистической регрессии являются вероятности принадлежности к классам (текущие значения прогнозов между 0 и 1). Эти вероятности основываются на соотношении беременных и «не-беременных» покупателей, равном 50/50 в нашей ребалансированной обучающей выборке.

Это вполне приемлемо, так как все, что вам нужно – это бинарная классификация по какому-нибудь ограничительному признаку, а не настоящие вероятности.

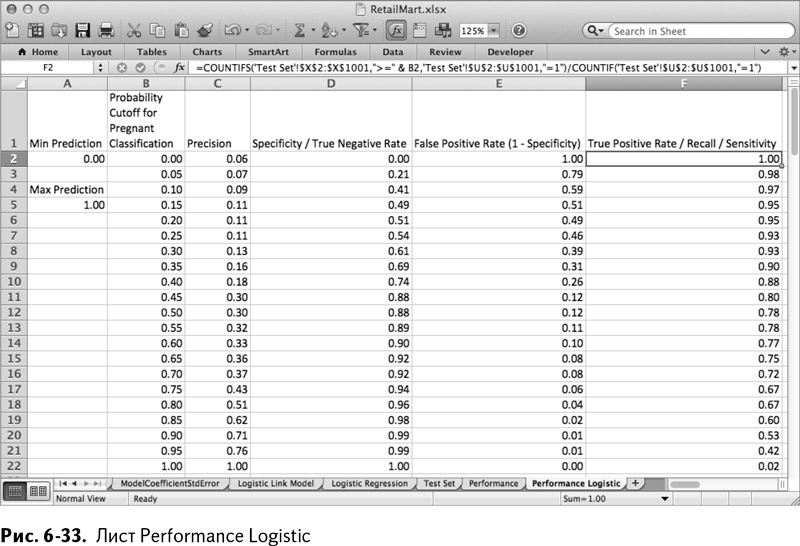
Выберите граничные значения от 0 до 1 с шагом в 0,05 (на самом деле стоило бы 1 поменять на 0,999 или около того, чтобы избавить формулу точности от деления на 0). Все строки ниже 22 можно очистить, а параметры качества работы нужно изменить только в том, чтобы они обращались к столбцу Х листа Test Set, вместо столбца V. Таким образом у нас получается лист, изображенный на рис. 6-33.

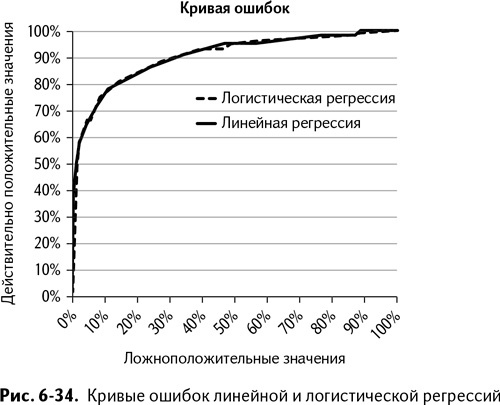
Вы можете построить кривую ошибок в точности так же, как и раньше. Однако, чтобы сравнить логистическую регрессию с линейной, нужно добавить ее ряд данных для параметров каждой модели (клик правой клавишей мыши на графике и выбор опции «Выбрать данные»). На рис. 6-34 хорошо видно, что кривые ошибок обеих моделей буквально сливаются.

При том что качество моделей практически идентично, вы можете склониться к использованию логистической регрессии разве что по причине практичности – ведь на выходе получаются текущие вероятности принадлежности к классам от 0 до 1. Это приятнее, при прочих равных.

Слово об осторожности

В реальном мире вы наверняка слышали многое мнений о выборе модели. Кто-то спросит: «А почему вы не воспользовались методом опорных векторов, нейронными сетями или случайными лесами деревьев с добавленными градиентами?» Типов моделей ИИ множество, и у каждой есть сильные и слабые стороны. Неплохо было бы попробовать некоторые из них в своей работе.

Но!

Испытание различных моделей ИИ – не самая важная часть проекта моделирования ИИ. Это последний этап, вишенка на торте. И именно в этот момент сайты вроде Kaggle.com (сайт состязаний по моделированию ИИ) делают все не так.

Вы получаете гораздо большую отдачу, когда тратите время на выбор хороших данных и отличительных признаков для вашей модели. К примеру, в задаче, приведенной в этой главе, вам бы лучше было обойтись тестированием возможных отличий вроде «покупатель перестал покупать мясо на ужин из-за боязни пастереллёза» и проверкой обучающих данных, чем тестированием нейронной сети на старом наборе для обучения.

Почему? Да потому, что пословица «Что посеешь, то и пожнешь» ни к чему не подходит так хорошо, как к ИИ. Модель ИИ – не волшебный помощник, она не может «проглотить» ужасную выборку и чудесным образом указать, как использовать эти данные. Поэтому сделайте одолжение своей модели ИИ – проявите изобретательность и найдите самые лучшие отличительные черты, какие только возможно.

Назад: Определение беременных покупателей РитейлМарта с помощью линейной регрессии

Дальше: Дополнительная информация