Книга: Много цифр. Анализ больших данных при помощи Excel
Назад: Числовое значение ребра: очки и штрафные в модулярности графа
Дальше: Туда и обратно: история Gephi
Переходим к кластеризации!
Теперь у вас есть все необходимые значения. Все, что вам нужно сделать – это запустить оптимизационную модель, чтобы найти оптимальное распределение по группам.
Буду заранее честен с вами. Нахождение оптимальных групп с помощью модулярности графа требует несколько более сложной подготовки оптимизации, чем вы встречали в главе 2. Подобные задачи часто решаются сложной эвристикой, вроде популярного лувенского метода (подробнее здесь: http://perso.uclouvain.be/vincent.blondel/research/louvain.html), но в этой книге я обещал не заставлять вас писать код, так что придется обходиться «Поиском решения».
Мы будем атаковать задачу с помощью метода под названием разделяющая кластеризация, или иерархическое разбиение. Для начала необходимо найти наилучший способ разделения графа на две группы. Затем мы разделим эти группы на четыре, и т. д., до тех пор, пока «Поиск решения» не заключит, что наилучший способ максимизации модулярности – это перестать делить группы.
Заметка
Разделяющая кластеризация – это противоположность другому известному методу – агломеративной кластеризации. Если бы мы решали задачу таким методом, то каждый покупатель образовывал бы собственный кластер, а вы раз за разом объединяли бы по два ближайших кластера, пока цель не оказалась достигнутой.
Деление 1
Итак, мы начинаем наш процесс разделяющей кластеризации с разделения графа на две группы, чтобы максимизировать модулярность.
Создайте новый лист под названием Split1 и вставьте покупателей в столбец А. Принадлежность каждого покупателя к группе будет обозначена в столбце В, который нужно назвать Community. Так как вы делите граф пополам, пусть этот параметр будет бинарной переменной решения в «Поиске решения», где значение 0/1 будет означать принадлежность к группе 0 или 1. Ни одна из групп не лучше другой. Нет ничего плохого в том, чтобы быть в 0 группе.
Считаем принадлежность каждого покупателя к группе
В столбце С вычислим модулярность для каждого покупателя при отнесении его к соответствующей группе. Я имею в виду, если вы поместите Адамса в группу 1, то его часть общей модулярности будет суммой всех значений ячеек его строки во вкладке Scores, покупатели в которых также отнесены к группе 1.
Рассмотрим, как добавить эту модулярность в формулу. Если Адамс в группе 1, то вам нужно сложить все значения ячеек из строки 2 вкладки Scores, которые относятся к другим покупателям, также попавшим в группу 1. Так как мы присваиваем только 0/1, можно использовать SUMPRODUCT/СУММПРОИЗВ для умножения вектора группы на вектор модулярности и сложения результата.
Хотя значения модулярностей расположены слева направо, в оптимизационной модели они идут сверху вниз, так что здесь придется использовать TRANSPOSE/ТРАНСП (что, в свою очередь, означает использование формулы массива):
{=SUMPRODUCT(B$2:B$101,TRANSPOSE(Scores!B2:CW2))}
{=СУММПРОИЗВ(B$2:B$101,ТРАНСП(Scores!B2:CW2))}
Формула умножает значения модулярности на значения принадлежности к группе. Остаются только те, которые относятся к членам группы 1, в то время как остальные обращаются в 0. SUMPRODUCT/СУММПРОИЗВ складывает все.
Но что, если Адамс был отнесен к группе 0? Нужно всего лишь транспонировать принадлежность к группам путем вычета их из 1, чтобы заставить работать суммы модулярностей.
{=SUMPRODUCT(1-(B$2:B$101),TRANSPOSE(Scores!B2:CW2))}
{=СУММПРОИЗВ(1-(B$2:B$101), ТРАНСП(Scores!B2:CW2))}
В идеальном мире вы бы могли соединить эти две формулы с помощью функции IF/ЕСЛИ, которая бы проверила принадлежность Адамса к той или иной группе, а затем использовала бы соответствующую формулу для сложения модулярностей тех или иных соседей. Но при использовании IF/ЕСЛИ пришлось бы задействовать нелинейную модель в «Поиске решения» (подробнее в главе 4). В данном случае максимизация модулярности слишком тяжела для нелинейного «Поиска решения», и он становится неэффективен. Следует сделать задачу линейной.
Приводим расчет модулярности в линейную форму
Если вы внимательно читали главу 4, то, конечно, помните метод моделирования формулы IF/ЕСЛИ с использованием линейных ограничений, таких как «большое М». Здесь мы тоже им воспользуемся.
Обе предыдущие формулы линейны, так почему бы просто не установить переменную модулярности для Адамса – такую, чтобы она была меньше их обеих? Мы пытаемся максимизировать общую модулярность, поэтому модулярность Адамса будет стремиться вверх, пока не наткнется на меньшую из ограничивающих формул.
Но как понять, который из расчетов модулярности, относящихся к принадлежности Адамса к группе, наименьший? Никак.
Чтобы разобраться с этим, вам нужно понять, которая из этих двух формул не используется. Если Адамс отнесен к 1, то первая формула становится верхней границей, а вторая формула отключается. Если у Адамса 0, то наоборот.
Как выключается одна из двух верхних границ? Добавьте в него «большое М» – настолько большое, чтобы в сравнении с ним верхней границей можно было бы пренебречь, потому что настоящая граница располагается ниже.
Посмотрите на эту модификацию первой формулы:
{=SUMPRODUCT(B$2:B$101,TRANSPOSE(Scores!B2:CW2))+
+(1-B2)*SUM(ABS(Scores!B2:CW2))}
{=СУММПРОИЗВ(B$2:B$101,ТРАНСП(Scores!B2:CW2))+
+(1-B2)*СУММ(ABS(Scores!B2:CW2))}
Если Адамс отнесен в группу 1, то последняя часть формулы обращается в 0 (из-за умножения на 1–В2). В этом случае формула становится идентичной первой формуле, которую мы рассматривали. Но если Адамса отнесли в группу 0, то эта формула больше не подходит и ее нужно отключить. Поэтому часть формулы (1-B2)*SUM(ABS(Scores!B2:CW2)//(1-B2)*СУММ(ABS(Scores!B2:CW2) добавляет 1, умноженную на сумму всех абсолютных значений модулярности, которые Адамс может получить. Это действие гарантирует, что результат окажется выше, чем у ее перевернутой версии, которая работает теперь:
{=SUMPRODUCT(1-(B$2:B$101),TRANSPOSE(Scores!B2:CW2))+
+B2*SUM(ABS(Scores!B2:CW2))}
{=СУММПРОИЗВ(1-(B$2:B$101), ТРАНСП(Scores!B2:CW2))+
B2*СУММ(ABS(Scores!B2:CW2))}
Все, что вы делаете – это заставляете модулярность Адамса быть меньше или равной правильному расчету и удаляете другую формулу из рассуждения, завышая ее значение. Это взломанная парнями из подворотни функция IF/ЕСЛИ.
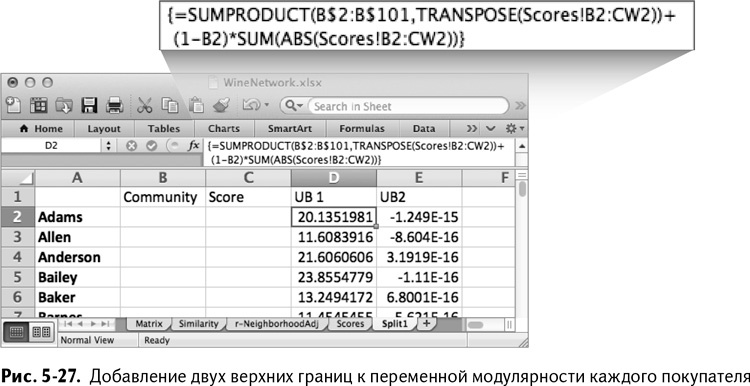
Таким образом, столбец С вы можете сделать столбцом модулярности, которая будет переменной решения, а в столбцы D и Е вашей электронной таблицы вставить эти две формулы в качестве верхних границ модулярности (рис. 5-27).
Обратите внимание, что в значениях принадлежности к группам в формуле используются абсолютные ссылки, так что без проблем растягивайте формулу вниз – ничего не изменится.
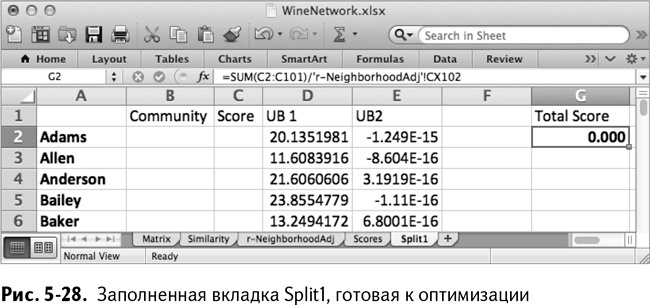
Складывая значения модулярности в столбце G2 для каждого отнесенного к группе в столбце С, можно получить их общее значение и нормализовать его по общему числу «пеньков» в r-NeighborhoodAdj'!CX102, чтобы закончить вычисление:
=SUM(C2:C101)/'r-NeighborhoodAdj'!CX102
=СУММ(C2:C101)/'r-NeighborhoodAdj'!CX102
В результате у нас получается лист, изображенный на рис. 5-28.
Запускаем линейную программу
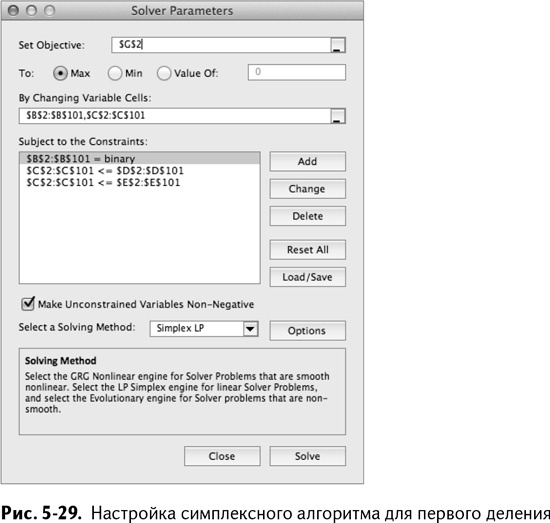
Теперь для оптимизации все готово. Откройте «Поиск решения» и отметьте, что вы максимизируете значение модулярности графа в ячейке G2. Переменные решения – это значения принадлежности к группе в В2:В101 и значения модулярности в С2:С101.
К значениям принадлежности к группе в В2:В101 нужно добавить условие бинарности. Также необходимо сделать переменные модулярности покупателей в столбце С меньше, чем обе верхние границы в столбцах D и Е.
Как показано на рис. 5-29, затем следует сделать все переменные неотрицательными, отметив галочкой эту опцию и выбрав «Поиск решения линейных задач симплекс-методом».
Одна из проблем использования ограничения «большого М» заключается в том, что у «Поиска решения» частенько возникают сомнения в том, что он на самом деле нашел оптимальное решение. Он будет продолжать крутить свои шестеренки, даже имея отличное решение в кармане. Чтобы этого не происходило, нажмите кнопку «Параметры» в «Поиске решения» и установите значение Max Subproblems на 15 000. Это гарантирует нам, что «Поиск решения» остановится минут через 20 после нажатия кнопки «Выполнить».
Жмите эту кнопку, независимо от того, чем вы пользуетесь – встроенным «Поиском решения» или OpenSolver (здесь кнопка находится на всплывающей боковой панели), – когда алгоритм завершит работу согласно ограничению, созданному пользователем. Он может сообщить вам, что нашел возможное решение, но оно не оптимальное. Это значит, что алгоритм просто не доказал оптимальность (точно так же на это не способны нелинейные алгоритмы), но не огорчайтесь: даже в этом случае можно быть уверенным, что решение не худшее.
Когда вы найдете решение, вкладка Split1 будет выглядеть, как показано на рис. 5-30.
При работе с Excel 2010 и 2013 следует использовать OpenSolver
Если вы пользуетесь Excel 2010 или 2013 под Windows, то эта задача слишком трудна для встроенного «Поиска решения», поэтому вам придется задействовать OpenSolver, как в главах 1 и 4.Если вы применяете OpenSolver, введите условия задачи в обычный «Поиск решения», но перед выполнением запустите плагин OpenSolver, чтобы «разогнать» вашу систему. У OpenSolver те же проблемы сограничением «большого М», так что перед запуском модели зайдите в параметры OpenSolver и установите ограничение времени на 300 секунд. Если вы этого не сделаете, OpenSolver будет пользоваться ограничением времени по умолчанию (а оно огромно) и вращать свои шестеренки, пока вам не захочется убить Excel.Если у вас MacOS и Excel 2007 или 2011, то вы вполне справитесь и обычным «Поиском решения», хотя, если можете, лучше воспользуйтесь OpenSolver в Excel 2007. Если у вас LibreOffice, то все будет в порядке.
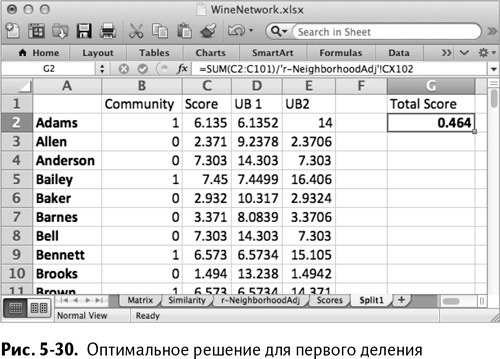
Мой поиск решения завершился на значении модулярности 0,464. Ваше решение может быть лучше, особенно если вы используете OpenSolver. Просматривая столбец В, вы видите, кто оказался в группе 0, а кто – в группе 1. Теперь встает вопрос: окончательное ли это решение? Действительно ли группы всего две или все же больше?
Чтобы ответить на этот вопрос, вам стоит попытаться разделить эти группы пополам. Если решение окончательное, то «Поиск решения» не найдет больше групп. Но если разделение этих групп на три или четыре улучшит модулярность, то пусть «Поиск решения» так и сделает.
Деление 2: электролатино!
Разделим эти группы так, как делят ячейку. Начнем с копирования листа Split1 в новый лист и переименования его в Split2.
Первое, что здесь нужно сделать – это вставить новый столбец после столбца со значениями принадлежности к группам (В). Назовите этот новый столбец С Last Run и скопируйте туда значения из В. Таким образом получается лист, изображенный на рис. 5-31.
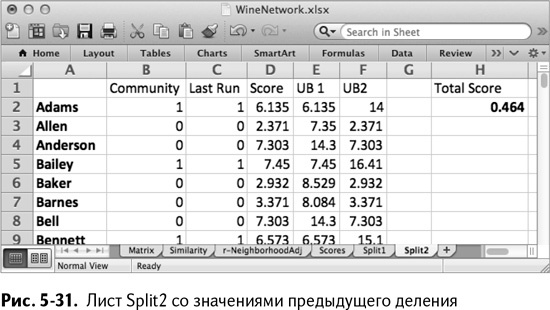
В этой модели подход тот же самый: каждому покупателю присваивается 1 или 0. Но стоит помнить, что если два покупателя получают в этот раз 1, это вовсе не значит, что они находятся в одной группе. Если в предыдущем делении они могли находиться в разных группах, то этот принцип сохраняется.
Другими словами, единственное значение модулярности, которое может получить Адамс, будучи, скажем, в группе 1–0, зависит от покупателей, отнесенных в группу 0 в первом делении и в группу 1 во втором. Таким образом, нам необходимо поменять верхние границы расчета модулярности. Расчет в столбце Е (здесь показан в Е2) теперь требует сверки с результатами предыдущего деления в столбце С:
{=SUMPRODUCT(B$2:B$101,IF(C$2:C$101=C2,1,0),
TRANSPOSE(Scores!B2:CW2))}
{=СУММПРОИЗВ(B$2:B$101,ЕСЛИ(C$2:C$101=C2,1,0),
ТРАНСП(Scores!B2:CW2))}
Логическое высказывание с оператором IF/ЕСЛИ IF(C$2:C$101=C2,1,0)/ЕСЛИ(C$2:C$101=C2,1,0) предотвращает начисление «очков» Адамсу, пока его соседи не окажутся с ним в первом делении.
Можно использовать этот оператор и здесь, потому что значения в столбце С больше не являются переменными решения. То деление было исправлено перед запуском, так что в этом нет ничего нелинейного. Добавьте оператор IF/ЕСЛИ в часть формулы с «большим М», чтобы сделать окончательный расчет в столбце Е:
SUMPRODUCT(B$2:B$101,IF(C$2:C$101=C2,1,0),TRANSPOSE
(Scores!B2:CW2))+(1-B2)*SUMPRODUCT(IF(C$2:C$101=C2,1,0),
TRANSPOSE(ABS(Scores!B2:CW2)))
СУММПРОИЗВ(B$2:B$101,ЕСЛИ(C$2:C$101=C2,1,0), ТРАНСП
(Scores!B2:CW2))+(1-B2)ЧСУММПРОИЗВ(IF(C$2:C$101=C2,1,0),
ТРАНСП(ABS(Scores!B2:CW2)))
Точно так же можно добавить этот оператор во вторую верхнюю границу в столбце F:
=SUMPRODUCT(1-(B$2:B$101),IF(C$2:C$101=C2,1,0),TRANSPOSE
(Scores!B2:CW2))+B2*SUMPRODUCT(IF(C$2:C$101=C2,1,0),
TRANSPOSE(ABS(Scores!B2:CW2)))
=СУММРПРОИЗВ(1-(B$2:B$101), ЕСЛИ(C$2:C$101=C2,1,0), ТРАНСП
(Scores!B2:CW2))+B2*СУММПРОИЗВ(ЕСЛИ(C$2:C$101=C2,1,0),
ТРАНСП(ABS(Scores!B2:CW2)))
Совершенные нами действия можно назвать консервацией задачи: те, кто попал в группу 0 при первом делении теперь находятся в своем собственном мирке модулярностей, равно как и те, кого отнесли к группе 1 в первый раз.
А вот и хорошая новость: в «Поиске решения» не нужно менять совсем ничего! Те же настройки, те же формулы. Если вы использовали OpenSolver, то он мог не сохранить настройки ограничения по времени из предыдущего расчета. Настройте его снова на 300 секунд. Нажмите «Выполнить».
В этот раз в Split2 у меня получилась модулярность, равная 0,546 (рис. 5-32), что является существенным улучшением по сравнению с 0,464. Это значит, что второе деление было хорошей идеей. (Ваше решение может отличаться и быть даже лучше моего.)
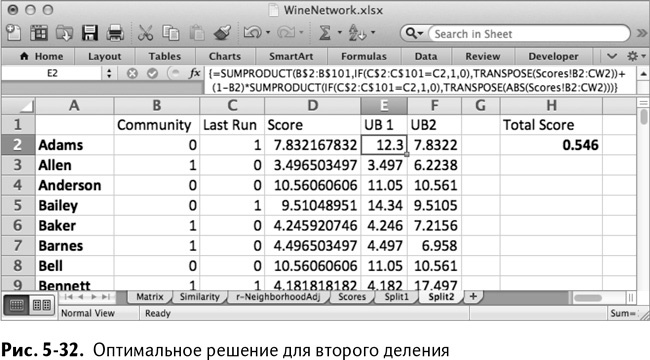
И… деление 3: возмездие
Хорошо, но стоит ли нам останавливаться на этом или стоит продолжить? Единственный способ узнать ответ – поделить еще раз. Если результат не будет лучше, чем 0,564 – значит, это конец.
Начнем с создания листа Split3, переименования Last Run в Last Run 2 и вставки нового Last Run в столбец С. Затем скопируем значения из В в С.
Добавим еще пару операторов IF//ЕСЛИ в верхние границы, чтобы проверять принадлежность к группе в предыдущем делении. Например, F2 превращается в следующее:
=SUMPRODUCT(B$2:B$101,IF(D$2:D$101=D2,1,0),
IF(C$2:C$101=C2,1,0),TRANSPOSE
(Scores!B2:CW2))+(1-B2)*SUMPRODUCT
(IF(C$2:C$101=C2,1,0),IF(D$2:D$101=D2,1,0),
TRANSPOSE(ABS(Scores!B2:CW2)))
=СУММПРОИЗВ(B$2:B$101,
ЕСЛИ(D$2:D$101=D2,1,0), ЕСЛИ(C$2:C$101=C2,1,0),
ТРАНСП(Scores!B2:CW2))+(1-B2)*СУММПРОИЗВ
(ЕСЛИ(C$2:C$101=C2,1,0), ЕСЛИ(D$2:D$101=D2,1,0),
ТРАНСП(ABS(Scores!B2:CW2)))
И снова настройки «Поиска решений» остаются неизменными. Установите максимальное время решения, если это необходимо, нажмите «Выполнить» и дайте модели сделать свое дело. В случае моей модели никакого улучшения модулярности не произошло (рис. 5-33).
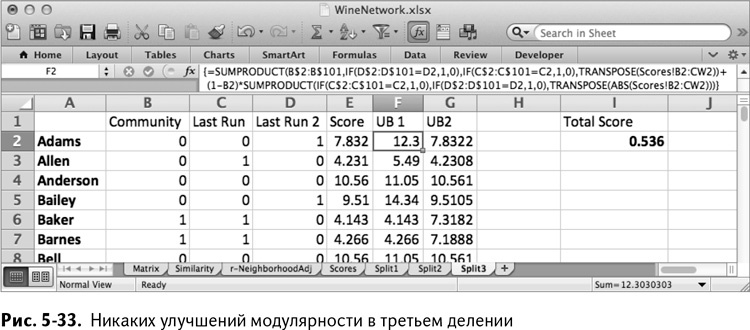
Очередное деление не добавило нам ничего. Это означает, что модулярность была эффективно максимизирована в предыдущем делении – Split2. Давайте рассмотрим принадлежности к группам из этой таблицы поподробнее.
Кодируем и анализируем группы
Первое, что нужно сделать для изучения принадлежностей к группам, – это взять наше бинарное дерево, созданное в процессе успешных делений, и сделать эти столбцы единичными ярлыками кластеров (групп).
Создайте вкладку под названием Communuties и вставьте туда имена покупателей, их группы и значения Last Run из вкладки Split2. Можете переименовать бинарные столбцы Split1 и Split2. Сделайте их бинарные значения числовыми, воспользовавшись чудо-формулой BIN2DEC//ДВ.В.ДЕС. В столбец D, начиная с D2, можно добавить:
=BIN2DEC(CONCATENATE(B2,C2))
=ДВ.В.ДЕС(СЦЕПИТЬ(B2,C2))
Копируя эту формулу вниз, можно получить принадлежности к группам, показанные на рис. 5-34 (ваши значения могут отличаться).
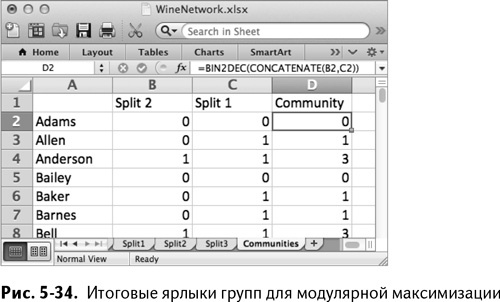
У нас получилось четыре кластера с ярлыками от 0 до 3 в десятеричной системе исчисления. Что же это за кластеры? Это можно выяснить тем же способом, что и в главе 2, – откопать наиболее популярные заказы покупателей, из которых эти кластеры состоят.
Для начала, в точности как в главе 2, создайте вкладку под названием TopDealsByCluster и вставьте информацию о сделках из столбцов от А до G вкладки Matrix. За ними, со столбца Н до К, поместите ярлыки кластеров – 0, 1, 2 и 3. Так у вас получается лист, изображенный на рис. 5-35.
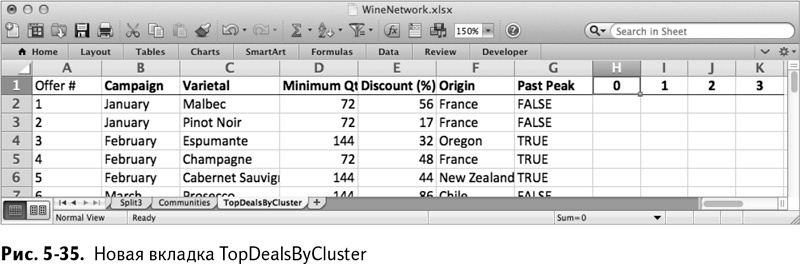
Для ярлыка 0 в столбце Н найдите всех покупателей из вкладки Communities, которые были отнесены к группе 0, и сложите количество покупателей для каждой сделки. Точно так же, как и в главе 2 и предыдущих вкладках про деление, используется SUMPRODUCT/СУММПРОИЗВ и оператор IF/ЕСЛИ, и в итоге получается следующее:
{=SUMPRODUCT(IF(Communities!$D$2:$D$101=
TopDealsByCluster!H$1,1,0),TRANSPOSE(Matrix!$H2:$DC2))}
{=СУММПРОИЗВ(ЕСЛИ(Communities!$D$2:$D$101=
TopDealsByCluster!H$1,1,0), ТРАНСП(Matrix!$H2:$DC2))}
В этой формуле проверяется количество покупателей, получивших 0 в столбце ярлыков Н1, а затем складываются значения по первой сделке – была ли она ими заключена, или нет – из промежутка Н2:С2 вкладки Matrix. Обратите внимание: для вертикального расположения используется функция TRANSPOSE/ТРАНСП. Это значит, что вычисления нужно будет производить, пользуясь формулами массива.
Также отметьте использование абсолютных ссылок в значениях принадлежности покупателей к группам, строки матрицы для заголовков и столбцы для информации о заказах. Это позволяет вам растянуть формулу вправо и вниз, чтобы получилась полная картина самых популярных сделок для каждого кластера (рис. 5-36).
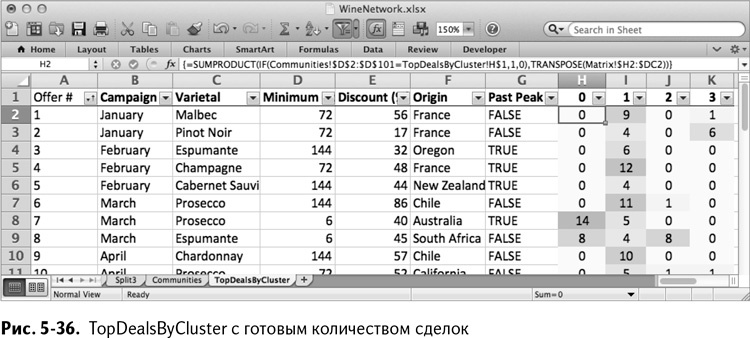
Как и в главе 2, к таблице следует применить фильтр и отсортировать результаты сделок в группе 0 в столбце Н от большего к меньшему. Результат изображен на рис. 5-37 – небольшая группа покупателей (ваши кластеры могут отличаться по порядку и составу, в зависимости от того, на каком решении «Поиск решения» заканчивал каждый шаг).
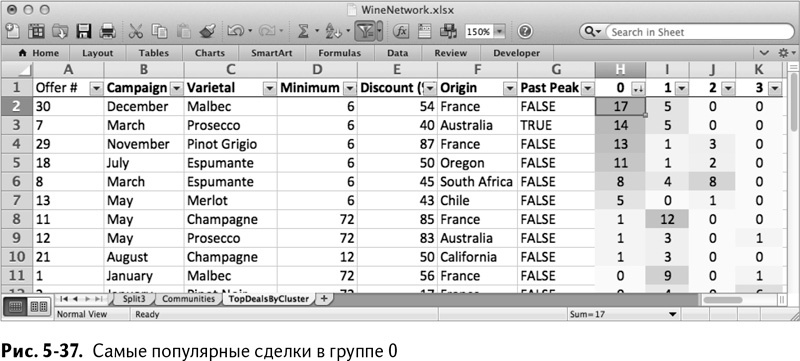
Сортируя группу 1, вы получаете нечто, очень похожее на объемный кластер французского Шампанского (рис. 5-38). Замечательно.
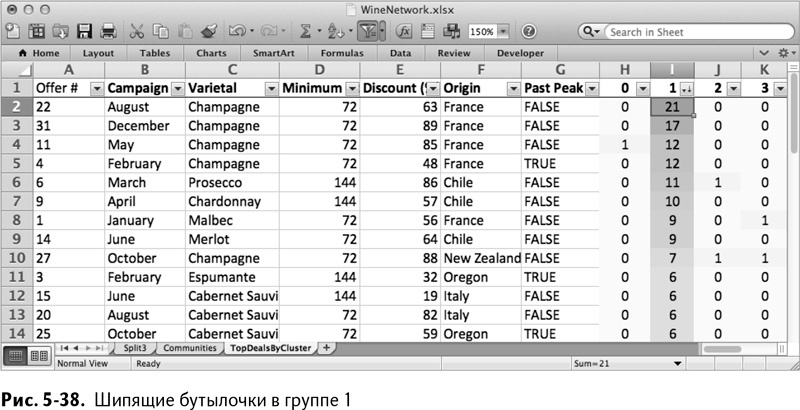
Что касается группы 2, то она выглядит похожей на группу 0, за исключением мартовской сделки по игристому вину – она основная (рис. 5-39).
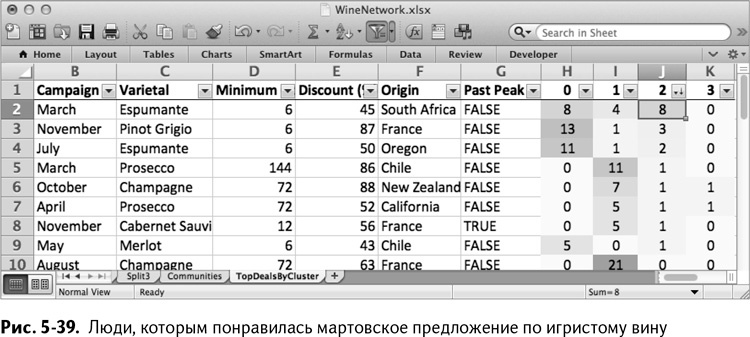
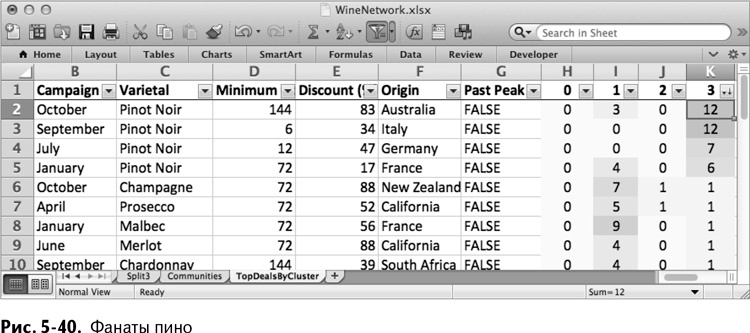
И группа 3 – любители пино нуар. Ребята, вы когда-нибудь слышали о каберне-совиньон? К сожалению, у меня отвратительный вкус во всем, что касается вина (см. рис. 5-40).
Вот и все! У вас четыре кластера, и, честное слово, три из них выглядят очень осмысленно, хотя я предполагаю возможное наличие группы людей, которые действительно просто захотели в марте игристое. И вы можете использовать это в своей работе – несколько нерасшифровываемых кластеров с выбросами.
Обратите внимание, как похоже это решение на уже найденное нами в главе 2. Но тогда мы пользовались кардинально другой методологией, сохраняя вектор сделок каждого покупателя и используя его для измерения расстояний от кластерного центра. Здесь же нет никакой концепции центра и даже совершенные покупателями сделки неочевидны. Важно расстояние до других покупателей.
Назад: Числовое значение ребра: очки и штрафные в модулярности графа
Дальше: Туда и обратно: история Gephi

