Книга: Много цифр. Анализ больших данных при помощи Excel
Назад: Строим граф из данных об оптовой торговле вином
Дальше: Переходим к кластеризации!
Числовое значение ребра: очки и штрафные в модулярности графа
Представьте, что я – покупатель, зависающий где-то в нашем графе, и хочу узнать, кто еще входит в мою группу.
Как насчет той дамы, связанной со мной ребром? Может быть. Наверное. Во всяком случае, мы связаны.
А что насчет того парня с другой стороны графа, с которым я соединен ребром? Хммм, гораздо менее вероятно.
Модулярность графа количественно выражает это интуитивное чувство, что группы определяются связями. Техника присваивает «очки» каждой паре вершин. Если две вершины не связаны, мне полагается штраф за расположение их в одной группе. Если две вершины связаны, нужно меня наградить. Какое бы я ни сделал предположение, модулярность графа использует сумму этих «очков» для каждой пары вершин, которые отнесены к одной и той же группе.
Используя алгоритм оптимизации (вы знали – не обойтись без «Поиска решения»!), вы можете «испытать» другие предположения о принадлежности к группам графа и посмотреть, которое из них наберет больше всего «очков» и меньше всего «штрафных». Это и будет выигрышной комбинацией модулярности.
Кто же такие «очки» и «штрафные»?
Применяя модулярную максимизацию, вы даете себе одно «очко» каждый раз, когда группируете в один кластер две вершины, имеющие общее ребро в матрице. И получаете ноль очков, если группируете две несвязанные вершины.
Проще простого.
Но что со штрафными?
Вот где алгоритм модулярной максимизации становится по-настоящему креативным. Вспомним наш граф «Друзей», изображенный на рис. 5–1.
Модулярная максимизация основывает свои штрафные на следующем утверждении, в котором фигурируют две вершины:
Если бы взяли этот граф и стерли бы на нем середины всех ребер, а затем соединили бы их заново случайным образом несколько раз, сколько бы в этом случае ребер получилось между двумя вершинами?
Вот это предполагаемое число и есть «штрафное».
Почему предполагаемое число ребер между двумя вершинами – это штраф? Да потому, что вы не собираетесь давать столько «очков» модели за группировку людей, основанную на отношениях, которые бы с большой вероятностью возникли, так как обе стороны чрезвычайно социальны.
Я хочу узнать, какая часть этого графа – это намеренные отношения и связи, а какая – нечто, произошедшее по причине «А, ну да, Чендлер связан с кучей людей, так что наверняка Фиби – одна из них». Это означает, что ребра между двумя очень разборчивыми людьми «менее случайны» и стоят больше, чем связи между двумя общительными.
Чтобы понять это яснее, посмотрите на версию графа «Друзей», в которой я стер середины ребер. Эти недоребра называются «пеньками» (рис. 5-21).
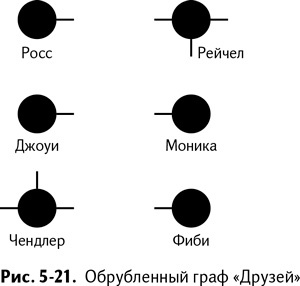
А теперь подумайте, как связать этот граф случайным образом. На рис. 5-22 я нарисовал один ужасный вариант. Да, при случайном соединении более чем вероятно соединение кого-то с собой самим, особенно если из их вершины торчит несколько «пеньков». Напоминает ужастик.
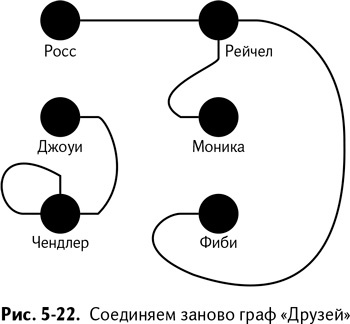
Рис. 5-22 – всего лишь один из возможных вариантов соединения, верно? Существует множество возможностей даже для графа, в котором всего пять ребер. Обратите внимание, что Росс и Рейчел снова вместе. Каковы были шансы, что это произойдет? Основываясь на той же вероятности, определим, каково предположительное число ребер между двумя вершинами, если вы соединяете граф заново снова и снова?
Для проведения случайного ребра нужно выбрать два случайных «пенька». Так какова вероятность того, что будут выбраны «пеньки» одной вершины?
Вот случай Рейчел: у нее три «пенька» из десяти возможных (это удвоенное количество ребер). У Росса всего один. Поэтому вероятность, что вы выберете Рейчел для любого ребра – 30 %, а вероятность, что вы выберете «пенек» Росса – 10 %. Вероятности выбора вершин показаны на рис. 5-23.

Так что если вы выбирали и связывали вершины случайным образом, то могли выбрать Росса, а затем Рейчел, или Рейчел, а затем Росса. Упростив, получаем 10 %, умноженные на 30 %, или 30 %, умноженные на 10 %, что является 2, умноженной на 0,3 и умноженной на 0,1. Выходит 6 %.
Но мы ведь рисуем не одно ребро, верно? Нужно нарисовать случайный граф с пятью ребрами, так что у вас есть пять попыток для выбора комбинации. Предполагаемое количество ребер между Россом и Рейчел в таком случае будет равно 6, умноженному на 5, или 0,3 ребра. Да, все верно, количество предполагаемых ребер может быть дробным.
Похоже, я взорвал ваш мозг в духе фильма «Начало». Допустим, я подброшу доллар Сакагавеи, который достанется вам, если выпадет орел, а не решка. 50 % за то, что вы его получите, а 50 % – нет. Ваш предполагаемый выигрыш – 0,5 × $1 = $0,50, даже при том, что на самом деле в этой игре вы никогда не выиграете 50 центов.
Аналогично и здесь – у вас просто есть графы, на которых Росс и Рейчел связаны, а есть такие, на которых нет, но тем не менее предполагаемое значение их общего ребра – 0,3.
Подробно эти расчеты показаны на рис. 5-24.
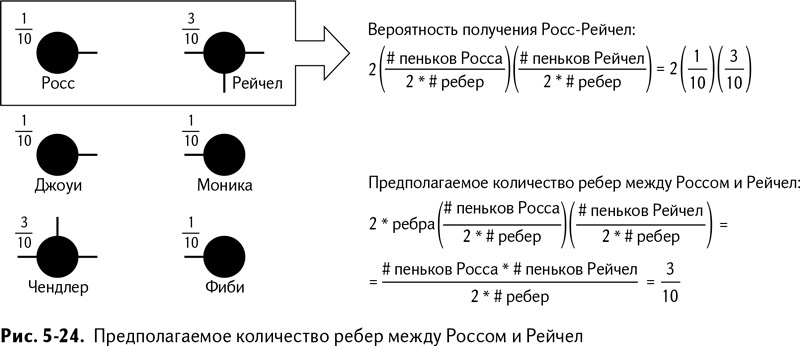
Если свести вместе «очки» и «штрафные», все должно проясниться.
Поместив Росса и Рейчел в одну группу, вы не получите целую 1. Это из-за штрафа в 0,3 очка, равного предполагаемому количеству ребер в случайном графе, которое они бы получили в любом случае. Так что вам остается 0,7.
Если вы не сгруппировали Росса и Рейчел, то скорее получите 0, чем 0,7.
С другой стороны, Рейчел и Фиби не связаны. Но у них все та же вероятность общего ребра – 0,3. Это означает, что если вы поместите их в одну группу, то все равно получите штраф, но вот очков не заработаете, так что в итоге выходит –0,3.
Почему? Потому что факт отсутствия ребра между Рейчел и Фиби что-то значит! Предполагаемое число ребер равнялось 0,3, но на этом графе их нет, так что в итоге это возможно намеренное разделение должно считаться.
Если вы не поместили Рейчел и Фиби в одну группу, то ни одна из них не получит никаких очков, так что при прочих равных лучше бы вам поместить их в два разных кластера.
Подводя итог, можно сказать, что «очки» и «штрафные» отражают то, насколько фактическая структура графа отличается от предполагаемой. Нужно определить группы, которые отвечают за эти различия.
Модулярность определения групп – это просто сумма этих «очков» и «штрафных» для пар вершин, помещенных в одну и ту же группу, разделенная на общее количество «пеньков» в графе. Деление на количество «пеньков» сохраняет максимальную модулярность в пределах 1, вне зависимости от размеров графа, что облегчает сравнение разных графов между собой.
Подготовка к итоговому подсчету
Но хватит слов! Давайте рассчитаем модулярность для каждой пары покупателей на графе.
Для начала сосчитаем, сколько «пеньков» у каждого покупателя и сколько всего «пеньков» в нашем графе. Обратите внимание, что количество «пеньков» покупателя – это просто степень его вершины.
Во вкладке r-NeighborhoodAdj вы можете подсчитать степень вершины простым суммированием столбца или строки. Если там 1, то это ребро, следовательно, «пенек», а значит – он посчитан. Так, например, сколько «пеньков» у Адамса? Можно просто поместить в ячейку В102 следующую формулу – и ответ найден:
=SUM(B2:B101)
=СУММ(B2:B101)
Получается 14. Точно так же можно просуммировать строку 2, поместив в формулу СХ2:
=SUM(B2:CW2)
=СУММ(B2:CW2)
В этом случае тоже получается 14, и это то, чего мы ожидали, так как граф неориентированный.
Копируя эти формулы вниз и вправо соответственно, вы можете подсчитать «пеньки» для каждой вершины. А суммируя столбец СХ в строке 102 можно получить общее количество «пеньков» на графе. Как показано на рис. 5-25, всего в графе 858 «пеньков».
Теперь, имея количество «пеньков», создайте вкладку Scores в вашей электронной таблице, куда затем вставьте и имена покупателей – в строку 1 и столбец А, в точности как во вкладке r-NeighborhoodAdj.
Рассмотрим ячейку В2, в которой находится модулярность Адамса относительно себя самого. Получает ли он «очко» или нет? На самом деле это можно прочитать в матрице смежности, 'r-NeighborhoodAdj'!B2. Если значение в матрице смежности –1, то она просто копируется. Элементарно.
Что же касается подсчета предполагаемого количества ребер, которое вам нужно в качестве «штрафных», то они подсчитываются точно так же, как показано на рис. 5-24:
вероятность покупателя А × вероятность покупателя В /общее количество «пеньков»
Сводя вместе эти «очки» и «штрафные» в ячейке В2, вы приходите к такой формуле:
='r-NeighborhoodAdj'!B2-
(('r-NeighborhoodAdj'!$CX2*'r-NeighborhoodAdj'!B$102)/
'r-NeighborhoodAdj'!$CX$102)
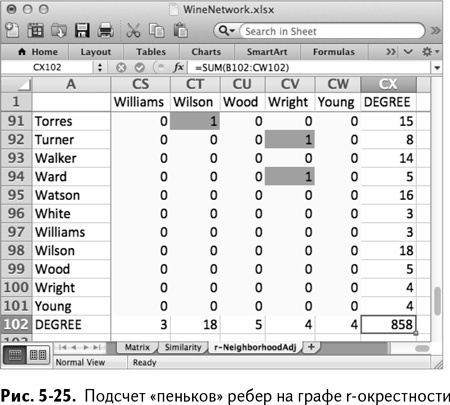
Получилось 0/1 по смежности минус предполагаемое количество.
Обратите внимание, что в формуле использованы абсолютные ссылки на ячейки с количеством «пеньков», так что если вы перемещаете формулу, все в ней меняется соответствующим образом. Растягивая ее вниз и вправо, вы получаете значения, показанные на рис. 5-26.
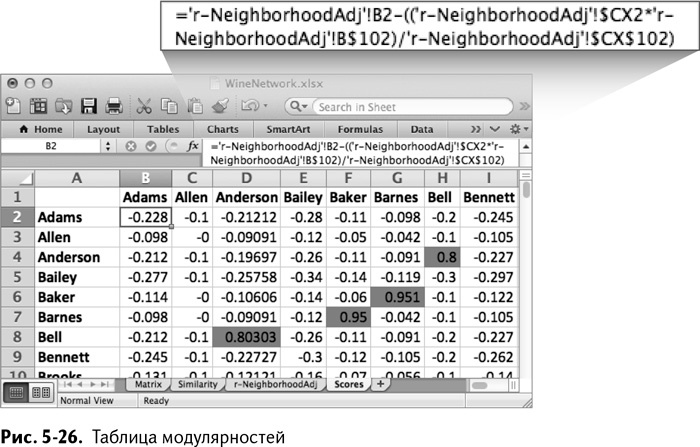
Для проверки обратимся к ячейке К2. В ней находится модулярность для кластеризации Адамс/Браун. Значение – 0,755.
Адамс и Браун имеют общее ребро в матрице смежности, так что вы получаете 1 очко за их кластеризацию в одну группу ('r-NeighborhoodAdj'!K2 в формуле), но у Адамса 14 «пеньков», а у Брауна – 15, так что их предполагаемое количество ребер равно 14 × 15 / 858. Эта вторая часть формулы выглядит так:
(('r-NeighborhoodAdj'!$CX2*'r-NeighborhoodAdj'!K$102)/
'r-NeighborhoodAdj'!$CX$102)
что оказывается равным 0,245. Сводя все вместе, получаем 1–0,245 = 0,755.

