Книга: Много цифр. Анализ больших данных при помощи Excel
Назад: Краткое введение в Gephi
Дальше: Числовое значение ребра: очки и штрафные в модулярности графа
Строим граф из данных об оптовой торговле вином
Заметка
Таблица Excel, использованная в этой главе, доступна для скачивания на сайте книги, . Она содержит исходные данные, на случай если вы хотите работать с ней. Если нет – просто следите за мной, используя уже заполненные листы.
В этой главе я продемонстрирую, как можно определить кластеры в ваших данных о заказах с помощью представления их в виде графа. В некоторых видах бизнеса данные (такие как медицинские, с направлениями от одного специалиста к другому, которые я упоминал ранее) уже имеют форму графа.
Но в этом случае матрица заказов вина из главы 2 не отражает отношений между покупателями напрямую.
Для начала нужно сформулировать, как нам изобразить набор данных о продаже вина в виде сети. Имеется в виду конструирование некоей матрицы смежности, вроде той, что мы делали для «Друзей» (рис. 5–2). Оттуда вы сможете визуализировать и рассчитать все, что угодно, относящееся к графу.
Я выбираю анализ с помощью вкладки Matrix в таблице WineNetwork.xlsx (доступной для скачивания вместе с этой книгой). Если помните, это та же самая вкладка Matrix, которую вы создали в начале главы 2 из транзакционных данных о продаже вина и оптовых метаданных.
Изображенные на рис. 5-13, строки вкладки Matrix дают нам информацию о 32 сделках по продаже вина, предложенных Винной Империей Джоуи Бэг О'Донатса в прошлом году. В столбцах таблицы расположены имена покупателей, а каждая ячейка (сделка, покупатель) имеет значение 1 в случае, если данный покупатель заключил данную сделку.
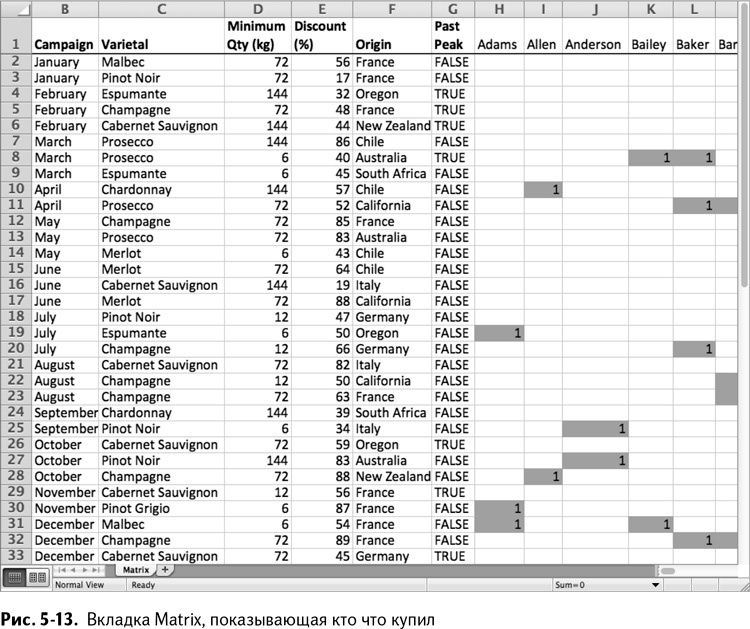
Вам нужно превратить эти данные из главы 2 во что-то, похожее на матрицу смежности «Друзей». С чего же начать?
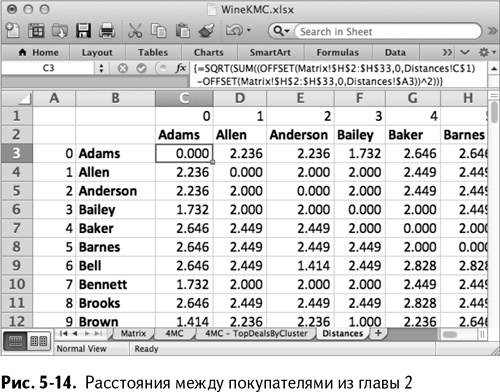
Вы уже делали нечто подобное, создавая матрицу расстояний для силуэта по k-средним в главе 2. Для этого расчета вы создавали матрицу расстояний между всеми покупателями, основываясь на заключенных ими сделках (рис. 5-14).
Этот набор данных был ориентирован на отношения «покупатель-покупатель», в точности как набор данных о «Друзьях». Связи между покупателями устанавливались по признаку того, как располагались их заказы.
Но есть пара проблем с матрицей расстояний между покупателями, созданной в главе 2:
• в конце главы 2 вы обнаружили, что в случае с данными о заказах асимметричное подобие и измерения расстояний между покупателями работают гораздо лучше евклидова расстояния. Вам важны заказы, а не их отсутствие;
• проведя ребро между двумя покупателями, вы руководствуетесь сходством этих покупателей, а не различиями между ними, поэтому данный расчет нужно «перевернуть». Эта близость заказов видна благодаря близости косинусов, поэтому вам нужно создать матрицу близости, то есть смежности, в противовес матрице расстояний из главы 2.
Создание матрицы близости косинусов
В этом разделе мы возьмем вкладку Matrix и сконструируем из нее граф «покупатель-покупатель» с помощью близости косинусов. В Excel этот процесс с использованием пронумерованных строк и столбцов и формулы OFFSET/СМЕЩ идентичен тому, что использовался в главе 2 для построения таблицы евклидовых расстояний. Подробнее о функции OFFSET/СМЕЩ читайте в главе 1.
Начнем с создания вкладки под названием Similarity, в которую вставим сеть из покупателей, где каждый пронумерован во всех направлениях. Не забывайте, что копирование и вставка покупателей из вкладки Matrix соответственно строкам возможно только с использованием меню «Специальная вставка» и галочки в поле «Транспонировать».
Готовая пустая сетка показана на рис. 5-15.
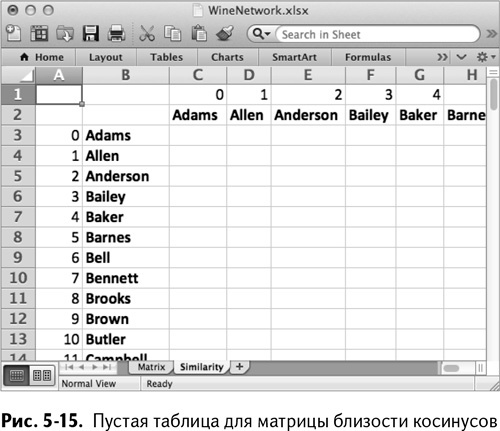
Начнем с вычисления близости косинусов между Адамсом и им же самим (которая должна равняться 1). Освежим в памяти определение близости косинусов между бинарными заказами двух покупателей, которое давалось в главе 2:
Количество совпадающих заказов по двум векторам, разделенное на произведение квадратного корня из количества заказов по первому вектору, умноженного на квадратный корень из количества заказов по второму вектору.
Вектор заказов Адамса – Matrix!$H$2:$H$33; так что для расчета близости косинусов в ячейке С3 используется следующая формула:
=SUMPRODUCT(Matrix!$H$2:$H$33,Matrix!$H$2:$H$33)/(SQRT(SUM
(Matrix!$H$2:$H$33))*SQRT(SUM(Matrix!$H$2:$H$33)))
=СУММПРОИЗВ(Matrix!$H$2:$H$33,Matrix!$H$2:$H$33)/(КОРЕНЬ(СУММ
(Matrix!$H$2:$H$33))*КОРЕНЬ(СУММ(Matrix!$H$2:$H$33)))
В начале формулы берется SUMPRODUCT/СУММПРОИЗВ из векторов заказа, которые вас интересуют, и рассчитывается количество совпавших заказов. В знаменателе перемножаются квадратные корни из количества заказов, сделанных каждым покупателем.
Теперь, когда эта формула работает для Адамса, вы можете растянуть ее на весь лист, чтобы не перепечатывать снова и снова. И для этого используется формула OFFSET/СМЕЩ. Заменяя Matrix!$H$2:$H$33 на OFFSET(Matrix!$H$2:
$H$33,0,Similarity!C$1)//СМЕЩ(Matrix!$H$2:$H$33,0,Similarity!C$1) для столбцов и OFFSET(Matrix!$H$2:$H$33,0,Similarity!$A3)//СМЕЩ(Matrix!
$H$2:$H$33,0,Similarity!$A3) для строк, вы получаете формулу, которая использует номера покупателей в столбце А и строке 1 для сдвига векторов заказа, применяемых в расчете близости.
Это приводит к несколько более уродливой (простите!) формуле для ячейки С3:
=SUMPRODUCT(OFFSET(Matrix!$H$2:$H$33,0,Similarity!C$1),
OFFSET(Matrix!$H$2:$H$33,0, Similarity!$A3))/(SQRT(SUM
(OFFSET(Matrix!$H$2:$H$33,0, Similarity!C$1)))*SQRT(SUM
(OFFSET(Matrix!$H$2:$H$33,0, Similarity!$A3))))
=СУММПРОИЗВ(СМЕЩ(Matrix!$H$2:$H$33,0,Similarity!C$1),
СМЕЩ(Matrix!$H$2:$H$33,0,Similarity!$A3))/(КОРЕНЬ(СУММ
(СМЕЩ(Matrix!$H$2:$H$33,0,Similarity!C$1)))*КОРЕНЬ(СУММ
(СМЕЩ(Matrix!$H$2:$H$33,0,Similarity!$A3))))
Эта формула фиксирует Matrix!$H$2:$H$33 как абсолютную ссылку, так что как бы вы ни двигали ее по таблице, она останется неизменной. Similarity! C$1 изменит номера столбцов, но будет оставаться в строке 1, как вы и планировали, а Similarity!$A3 останется в столбце А.
Но это еще не все. Вы хотели создать граф покупателей, которые похожи друг на друга, но наверняка не задумались о диагонали матрицы. Да, Адамс идентичен сам себе и имеет близость косинусов, равную 1, но вам не нужен граф с ребрами, которые замыкаются на ту же вершину, от которой исходят, поэтому придется сделать все подобные значения равными 0.
Это просто означает свертывание расчета близости косинусов в утверждение с IF/ЕСЛИ, чтобы проверить, не равняется ли покупатель в строке покупателю в столбце. Таким образом, итоговая формула выглядит так:
IF(C$1=$A3,0,SUMPRODUCT(OFFSET
Matrix!$H$2:$H$33,0,Similarity!
C$1),OFFSET(Matrix!$H$2:$H$33,0,Similarity!$A3))/(SQRT
(SUM(OFFSET(Matrix!$H$2:$H$33,0,Similarity!C$1)))*SQRT(SUM
(OFFSET(Matrix!$H$2:$H$33,0,Similarity!$A3)))))
ЕСЛИ(C$1=$A3,0,СУММПРОИЗВ(СМЕЩ(Matrix!$H$2:$H$33,0,Similarity!
C$1), СМЕЩ(Matrix!$H$2:$H$33,0,Similarity!$A3))/
(КОРЕНЬ(СУММ(СМЕЩ(Matrix!$H$2:$H$33,0,
Similarity!C$1)))*КОРЕНЬ(СУММ
(СМЕЩ(Matrix!$H$2:$H$33,0,Similarity!$A3)))))
Итак, теперь, когда у вас есть формула, которую можно перетаскивать куда угодно, возьмите ячейку С3 за нижний правый угол и растяните вправо до СХ3 и вниз до СХ102.
В итоге в вашем распоряжении – матрица близости косинусов, которая показывает, какие покупатели похожи. Применяя условное форматирование, получаем результат, показанный на рис. 5-16.
Построение графа N-соседства
Лист Similarity – это граф со значениями. Каждая пара покупателей имеет между собой или 0 или ненулевое значение близости косинусов, которое отображает толщину ребра между ними. Таким образом, мы видим, что матрица близости – это матрица смежности.
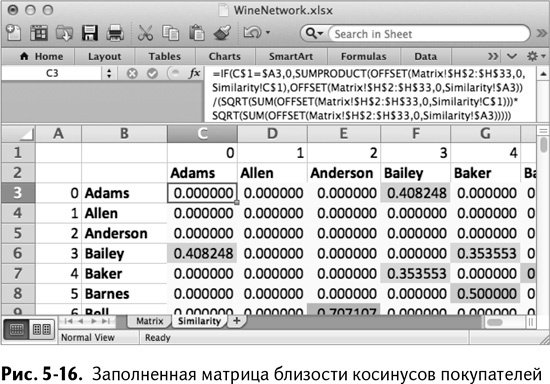
Так почему бы не вынуть эту матрицу смежности из таблицы и не вставить поскорее в Gephi? Может, вы уже настроились анализировать все на графе.
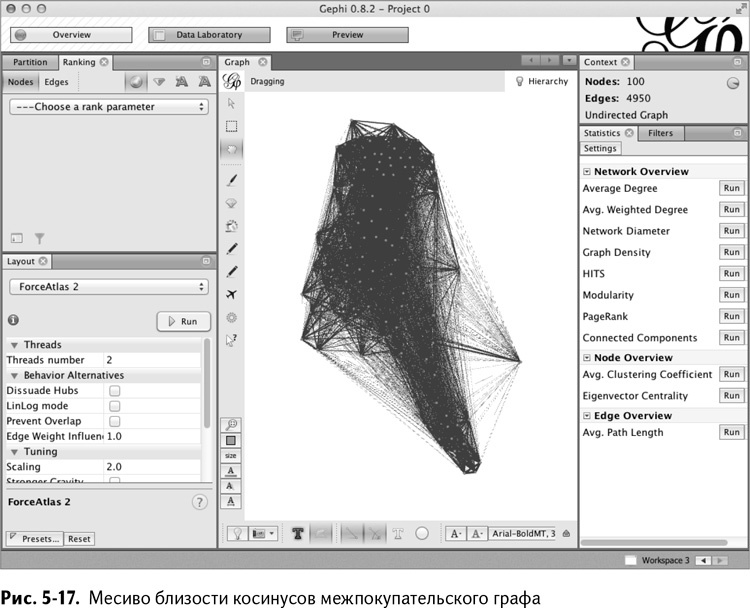
Конечно, экспорт CSV и дальнейший импорт в Gephi возможен и на этом этапе. Но позвольте мне предостеречь вас от такого шага и сразу показать картину графа (рис. 5-17) после импорта в Gephi. Это жуткая каша из ребер, торчащих отовсюду. Излишнее множество связей мешают алгоритму отображения правильно расположить вершины относительно друг друга, так что в итоге мы имеем неуклюжее месиво.
Вы заключили около 300 сделок и превратили их в тысячи ребер графа. Некоторые из них можно отнести к случайным. В самом деле, может, мы с вами совпали по одной сделке из десяти и у вас микроскопическая близость косинусов – так стоит ли проводить на графе это ребро?
Для придания нашим данным осмысленности удалите некоторые не особо значимые ребра и оставьте только самые крепкие связи – те, в которых есть еще что-то, кроме случайного удачного совпадения сделок.
Прекрасно, но какими именно ребрами можно пренебречь?
Существуют две популярные техники удаления ребер из сетевых графов. Можно взять матрицу смежности и построить одно из двух:
• граф r-окрестности: здесь мы оставляем только ребра определенной толщины. К примеру, в матрице смежности числовое значение ребра может изменяться от 0 до 1. Возможно, стоит избавиться от всех ребер со значениями меньше 0,5. Тогда получится пример графа r-окрестности с r = 0,5;
• граф k ближайших соседей (k nearest neighbors, kNN): в этом случае вы определяете максимальное число ребер, исходящих из одной вершины. Например, если установить k= 5, то при каждой вершине останутся только 5 ребер с наибольшими значениями.
Но ни тот, ни другой граф ничем не лучше второго. Все зависит от ситуации.
В этой главе я сфокусируюсь на первом варианте, графе r-окрестности. А второй вариант с kNN оставлю вам как упражнение для решения этой задачи другим способом. Его довольно просто выполнить в Excel, используя функцию LARGE/НАИБОЛЬШИЙ (более подробно эта функция описана в главе 1). В главе 9 мы также воспользуемся kNN для определения выбросов.
Так как же превратить вкладку Similarity в матрицу смежности r-окрестности? Для начала нужно определить r.
В белом поле под матрицей близости подсчитайте количество ребер (ненулевых значений близости), которые есть у вас в матрице смежности, с помощью функции в ячейке С104:
=COUNTIF(C3:CX102,">0")
=СЧЁТЕСЛИ(C3:CX102,">0")
Эта функция выдает нам 2950 ребер, созданных из исходных 324 сделок. Что, если оставить только 20 % с наибольшими значениями? Каким для этого должно быть r? Попробуем прикинуть: при 2950 ребрах 80-м перцентилем по близости будет примерно то, что соответствует 590-му ребру. Так что под расчетом количества ребер в С105 можно использовать функцию LARGE/НАИБОЛЬШИЙ, чтобы узнать значение 590-го по порядку уменьшения значений ребра (рис. 5-18):
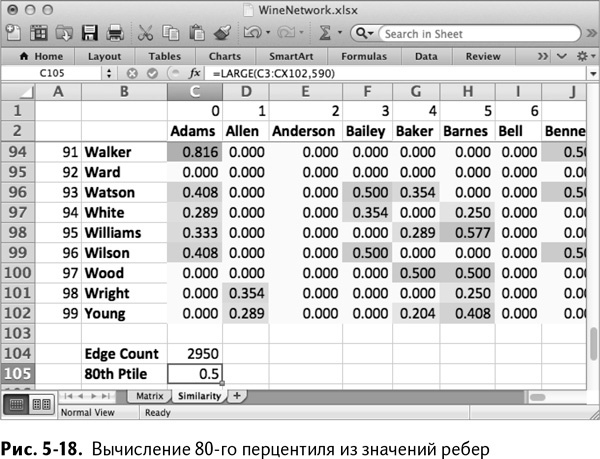
=LARGE(C3:CX102,590)
=НАИБОЛЬШИЙ(C3:CX102,590)
Функция выдает значение 0,5. Таким образом, можно оставить 20 % ребер с наибольшими значениями, просто отбросив все, значения близости косинусов которых меньше 0,5.
Теперь, когда с графа r-окрестности убрано все лишнее, сборка матрицы смежности будет очень простой. Создайте новый лист в вашей таблице и назовите его r-NeighborhoodAdj, а затем вставьте имена покупателей в столбец А и строку 1, чтобы получилась таблица.
В любой ячейке этой таблицы нужно поставить 1, если значение близости из предыдущей таблицы Similarity больше 0,5. Таким образом, к примеру, в ячейке В2 можно использовать такую формулу:
=IF(Similarity!C3>=Similarity!$C$105,1,0)
=ЕСЛИ(Similarity!C3>=Similarity!$C$105,1,0)
Функция IF//ЕСЛИ сравнивает соответствующие значения близости с величиной, выбранной нами как ограничение в Similarity!$C$105(0,5), и ставит 1, если эта величина достаточно велика. Так как Similarity!$C$105 содержит абсолютные ссылки, вы можете растянуть формулу на весь лист, чтобы заполнить матрицу целиком, как показано на рис. 5-19 (я использовал условное форматирование).
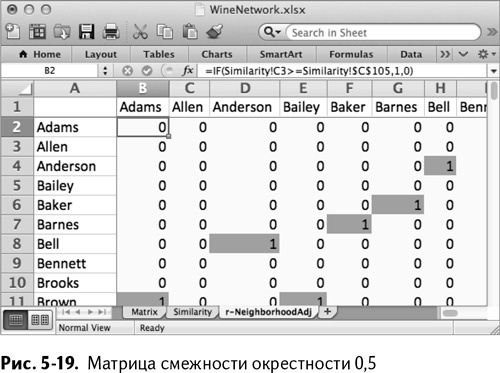
Теперь у вас есть граф r-окрестности данных о заказах покупателей. Вы трансформировали данные о заказах в отношения между покупателями и затем ограничили их до набора весьма значимых единиц.
Если бы вам нужно было сейчас экспортировать r-окрестность в матрицу смежности в Gephi и затем получить графическое изображение, то получилось бы гораздо лучше, чем в предыдущий раз, изображенный на рис. 5-17. Экспортируйте граф сами. Сделайте эти пару шагов с точкой с запятой и взгляните на результат вместе со мной.
Как показано на рис. 5-20, в графе есть по меньшей мере два тесно связанных сообщества, похожие на опухоли. Одно из них довольно сильно отделено от остальной массы, что прекрасно, потому что это значит: интересы его участников отличны от остальных покупателей.
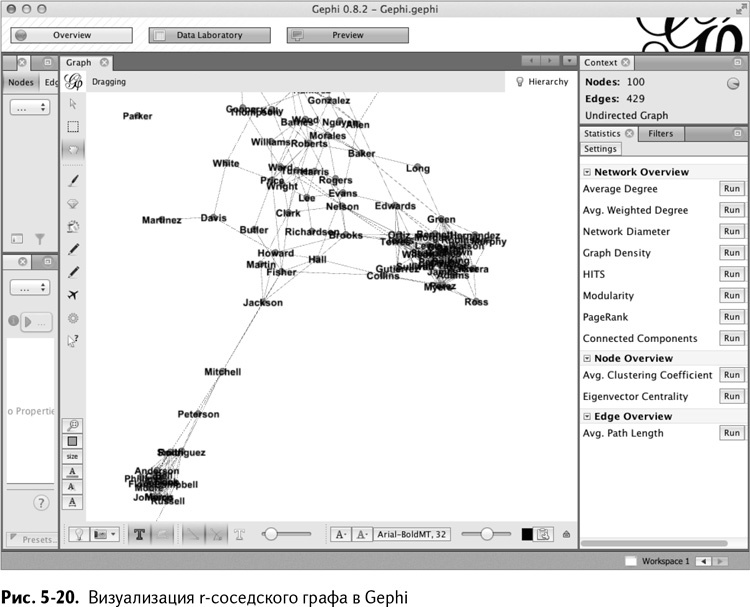
А здесь мы видим старого доброго Паркера, единственного покупателя, у которого не нашлось ребер с близостью косинусов большей или равной 0,5. Так что он сам по себе одиноко плачет в уголке. Мне, честно, неудобно за этого парня, потому что алгоритмы отображения стараются расположить его как можно дальше от связанной части графа.
Отлично! Итак, теперь у вас есть граф, который можно охватить взглядом. И на деле простое отображение графа и разглядывание его – зрительное разделение на группы – само по себе не так уж плохо. Вы взяли многомерные данные и дистиллировали их в нечто плоское, вроде пола актового зала из главы 2. Но если бы у вас были тысячи покупателей, а не сотни, глаза бы уже не так помогали. Конечно, даже сейчас на графе есть такие покупатели, которых трудно сгруппировать. В одной ли они группе или в нескольких?
И в этот самый момент в игру вступает модульная максимизация. Алгоритм использует отношения между людьми на графе, чтобы делать предположения об их принадлежности к той или иной группе, даже если граф не умещается в ваше поле зрения.
Назад: Краткое введение в Gephi
Дальше: Числовое значение ребра: очки и штрафные в модулярности графа

