Книга: Много цифр. Анализ больших данных при помощи Excel
Назад: Начнем с простого компромисса
Дальше: Моделируем риски
Свежий, из сада – прямо в стакан… с небольшой остановкой на модель смешивания
В вашем далеком детстве наверняка однажды наступил такой знаменательный день, когда вам сказали, что никакого Деда Мороза не существует, кроме того краснорожего ряженого дядьки на утреннике.
Заметка
Электронная таблица Excel, использованная в данной главе, OrangeJuiceBlending.xlsx, доступна на сайте книги, www.wiley.com/go/datasmart. Эта таблица содержит все необходимые для работы исходные данные. Или же вы можете просто читать и следить за мной по таблицам, которые я уже заполнил.
Так вот, сегодня я намерен разрушить еще один миф: ваш свежевыжатый сок премиум-класса, не восстановленный из концентрата, не был выжат вручную. На самом деле, мякоть в нем, скорее всего, из одних апельсинов, сок – из других, более того, он взят из разных бочек и смешан согласно математическим моделям, созданным для того, чтобы удостовериться, что каждый выпитый вами стакан имеет в итоге один и тот же вкус.
Одинаковый вкус апельсинового сока круглый год – далеко не пустяк, с которым справится каждый. Во-первых, апельсины не зреют во Флориде круглогодично. Во-вторых, разные сорта созревают в разное время. Сорвешь слишком рано – вкус слишком «зеленый». Закажешь апельсины из другой страны, где сейчас сезон – сок может быть другого цвета. Или слаще. Потребители требуют постоянства. Может быть, для какого-нибудь Sunny D это просто, но как достичь идеала вам с вашей кучей бочек холодного свежевыжатого сока?
Вы используете модель для смешивания
В известном телесериале «Аббатство Даунтон» богатый лорд Грэнтэм вкладывает все деньги семьи в один-единственный железнодорожный венчур. Рискованно. И он много теряет. Очевидно, в начале ХХ века диверсификация не была популярной идеей.
При усреднении рисков и возврате портфеля инвестиций по нескольким вложениям излишки по прибыльным направлениям не дадут вам внезапно разбогатеть, но меньше будут и излишки по убыточным направлениям, тянущие вас на дно. Точно такой же подход применим и к современному производству апельсинового сока.
Сок можно доставить со всего мира, и он будет из разных апельсинов разных сезонов. У каждого продукта свои особенности: один чуть терпкий, другой – немного вяжущий, а остальные могут оказаться чудовищно сладкими. И только смешиванием этого «портфолио» может быть достигнут постоянный вкус.
Вот проблема, с которой мы будем работать в этом разделе. Как построить модель смешивания, которая уменьшает стоимость и одновременно повышает качество? Какие типы инструментов следует задействовать при выполнении работ, которые по ходу дела постоянно требуют математической формулировки?
Начнем с характеристик
Допустим, вы – аналитик, работающий в ДжусЛэнде. Ваш босс, мистер Джус Р. Лэндингсли III (ваша компания страдает непотизмом), попросил вас распланировать закупки сока у поставщиков на январь, февраль и март наступающего года. Вместе с этим поручением мистер Лэндингсли протягивает вам список характеристик от поставщиков, содержащий страну происхождения и сорт, доступное для заказа количество на следующие три месяца и цену, а также стоимость пересылки за 1000 галлонов.
В списке приведены характеристики цвета сока по шкале от 1 до 10 и три вкусовых компонента:
• отношение Брикс/кислотность: Брикс – это мера сладости сока, так что Брикс/кислотность – это отношение сладости к терпкости (кислотности), что, в конце концов, и есть настоящий вкус апельсинового сока;
• кислотность (%): Кислотность в процентах от сока приведена отдельно, потому что это определенное количество: неважно, насколько сладок сок, если он при этом слишком кислый;
• вяжущий вкус (шкала 1–10): мера «неспелости» сока. Это тот горький, незрелый, садовый привкус, который может закрасться в сок. Этот параметр оценивается группой специалистов на каждом производстве по выпуску сока по шкале 1–10.
Все эти характеристики представлены в электронной таблице, изображенной на рис. 4-18.

Какой бы сок вы ни выбрали, он будет доставлен на ваше производство в огромных асептических охлажденных бочках, торговым кораблем или по железной дороге. Поэтому отсутствует стоимость пересылки для апельсинов «валенсия» из Флориды – фабрика, смешивающая сок, находится прямо в вашей флоридской апельсиновой роще (где в старые добрые времена вы сами выращивали все нужные вам апельсины).
Посмотрите на характеристики на рис. 4-18. Что вы можете о них сказать? Сок разных сортов и мест произрастания.
Некоторые соки, например, мексиканские, дешевые, но слишком вяжут. В других сортах, как например, техасский «санстар», сок слаще и вяжет меньше, но и цена его выше.
Выбор сока для заказа на следующие три месяца зависит от ответов на следующие вопросы:
• если вы минимизируете стоимость, сможете ли вы купить все, что захотите?
• Сколько сока вам нужно?
• Каковы ограничения по цвету и вкусу для каждой партии?
Возвращаемся к консистенции
С помощью вкусовых тестов и опроса покупателей ДжусЛэнд определил, как должен выглядеть сок и каким он должен быть на вкус. Небольшой выход за пределы этих характеристик – и покупатели почти наверняка сочтут ваш сок ненастоящим, дешевым или, хуже того, восстановленным из концентрата. Фу!
Мистер Лэндингсли III предъявляет вам следующие требования.
• Он хочет иметь план заказа по самым низким ценам на январь, февраль и март, соответствующий ожидаемому спросу в 600 000 галлонов сока в январе и феврале и 700 000 галлонов в марте.
• Он имеет договор со штатом Флорида, предоставляющим налоговые льготы при условии, что компания покупает не менее 40 % сока каждый месяц у фермеров, выращивающих сорт «флорида валенсия». Нарушать договор нельзя ни при каких условиях.
• Отношение Брикс/кислотность (BAR) должно оставаться в пределах между 11,5 и 12,5 в смеси каждого месяца.
• Уровень кислотности должен оставаться между 0,75 % и 1 %.
• Уровень вяжущего вкуса должен быть 4 или ниже.
• Цвет должен находиться в рамках 4,5–5,5. Не слишком темный, не слишком водянистый.
Из этих требований быстренько составляем план задачи для линейного программирования.
Цель: Минимизация закупочной стоимости.
Задача: Найти количество каждого сока для закупки каждый месяц.
Условия:
• спрос;
• поставки;
• договор со штатом Флорида;
• вкус;
• цвет.
Вводим данные в Excel
Чтобы смоделировать эту задачу в Excel, сперва создайте новый лист, на котором будет размещаться расчет. Назовем его Optimization Model.
В ячейку А2 под заголовком Total Cost поместите указатель поля для заполнения – там будет результат.
Под ней, в ячейку А5, вставьте таблицу характеристик таким образом, чтобы эти четыре столбца оказались между Region и Qty Available – создаем место для переменных решения и их сумм.
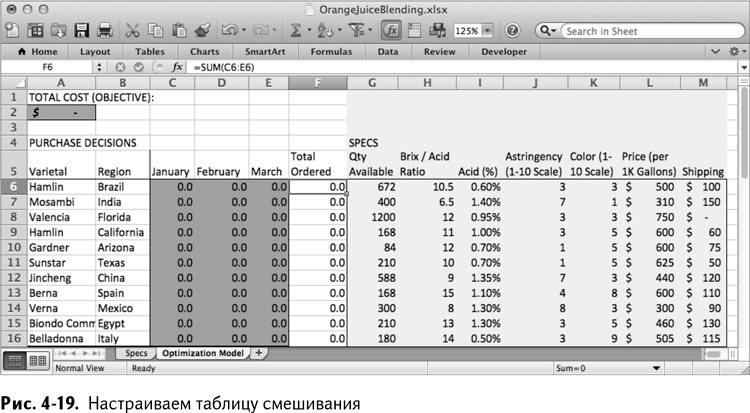
Первые три столбца назовите, соответственно, January, February и March, а четвертый, где будет их сумма, – Total Ordered. В этом столбце расположите сумму трех левых столбцов, что в случае с бразильским «гамлином» в ячейке F6 будет выглядеть так:
=SUM(C6:E6)
=СУММА(С6:Е6)
Можете растянуть ячейку F6 до F16. Применив условное форматирование на С6:Е 6, получаете таблицу, как на рис. 4-19.
Ниже полей с ежемесячными заказами добавьте поля для ежемесячных поставок и стоимости пересылки. Для января, к примеру, поместите стоимость пересылки в ячейку С17 следующим образом:
=SUMPRODUCT(C6:C16,$L6:$L16)
=СУММПРОИЗВ(C6:C16,$L6:$L16)
Так как переменные решения содержатся только в столбце С, вычисление снова будет линейным. Точно такую же формулу нужно добавить в С18 для расчета стоимости доставки за месяц:
=SUMPRODUCT(C6:C16,$M6:$M16)
=СУММПРОИЗВ(C6:C16,$M6:$M16)
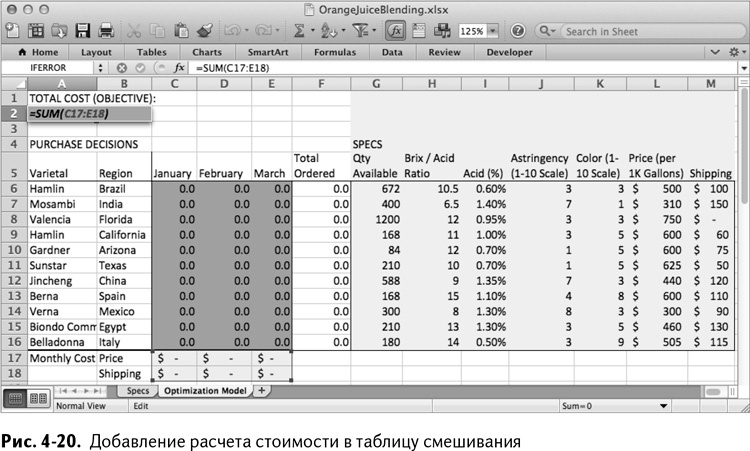
Растягивая формулы на столбцы D и E, вы получаете расчет стоимости поставок и доставки. Теперь можно установить в ячейку А2 целевую функцию суммы С17:Е18. Получившаяся таблица представлена на рис. 4-20.
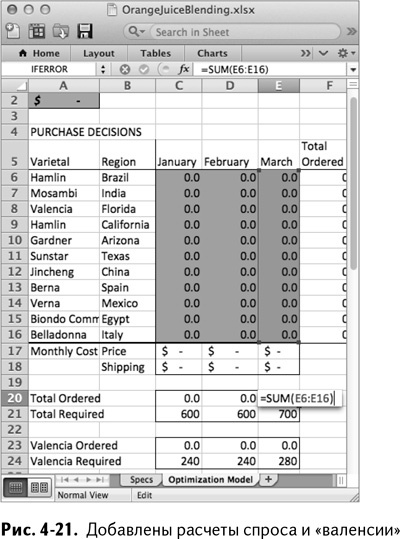
Теперь добавим расчеты для удовлетворения условиям спроса и продажи флоридской «валенсии». В строке 20 сложим общее количество сока, поставленное в этом месяце, а в строке 21 разместим требуемые уровни 600, 600 и 700 в столбцах С – Е, соответственно.
Что касается общего количества апельсинов «валенсия», заказанных у Флориды, то перенесите С8:Е8 на С23:Е23 и поместите необходимые 40 % общего спроса (240, 240, 280) под этими значениями.
Так мы получаем таблицу, изображенную на рис. 4-21.
Теперь, когда мы внесли в таблицу целевую функцию, переменные решения, поставки, спрос и расчет количества флоридской «валенсии», все, что нам осталось – это расчет по показателям вкуса и цвета, основанный на том, что же мы, собственно, заказываем.
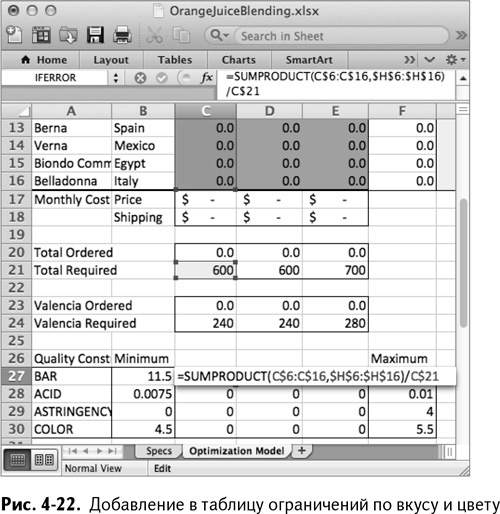
Начнем с отношения Брикс/кислотность. Поместите в ячейку В27 минимальное значение этого отношения в смеси, равное 11,5. Затем в ячейке С27 используйте SUMPRODUCT/СУММПРОИЗВ январских заказов (столбец С) и их отношения Брикс/кислотность в столбце Н, разделенные на общий спрос, – и вы получите среднее отношение Брикс/кислотность.
Внимание
Не делите на спрос последовательно, так как вообще спрос является функцией переменных решения. Решения, поделенные на решения, ужасно нелинейны!
Просто помните, что вы устанавливаете величину общего спроса, равную ожидаемому спросу, как ограничение, так что нет причины просто последовательно делить на спрос в процессе вычисления среднего отношения Брикс/кислотность для смеси. Таким образом, ячейка С27 выглядит так:
=SUMPRODUCT(C$6:C$16,$H$6:$H$16)/C$21
=СУММПРОИЗВ(C$6:C$16,$H$6:$H$16)/C$21
Можете растянуть эту формулу до столбца Е. В столбце F вы заканчиваете ряд, вбив максимальное значение этого отношения – 12,5. Затем можно повторить эти шаги для шкал кислотности, вязкости и цвета в строках с 28 по 30. Получившаяся таблица изображена на рис. 4-22.
Постановка задачи «Поиску решения»
Ну что ж, теперь у нас есть все необходимые данные и расчеты для постановки задачи смешивания. Первое, что нужно объяснить «Поиску решения», – это функция общей стоимости в А2, которую мы хотим минимизировать.
Переменные решения – это величины ежемесячных заказов каждого сорта, расположенные в ячейках С6:Е16. Снова напомню, что переменные не могут быть отрицательными, так что убедитесь, что поставили галочку «Сделать переменные без ограничений неотрицательными» («Линейная модель» в Excel 2007).
Когда дело доходит до добавления условий, задача начинает всерьез отличаться от примера с автоматами и маслом. А их множество.
Первое условие – заказы в строке 20 должны быть равны спросу в строке 21 за каждый месяц. Точно так же заказы на флоридскую «валенсию» в строке 23 должны быть больше или равны требуемому количеству в строке 24. Также общее количество заказов из каждого региона, рассчитанное в F6:F16, должно быть меньше или равно доступному для заказа количеству в G6:G16.
Итак, ограничения поставок и предложения установлены, теперь очередь вкуса и цвета.
Однако Excel не позволит вам ограничить два ряда с разной размерностью, поэтому если вы напечатаете C27:E30 ≥ B27:B30, он вас не поймет (что ужасно раздражает). Вместо этого нужно добавлять условия в столбцы С, D и Е по отдельности. К примеру, для январских заказов у вас есть условие C27:С30 ≥ B27:B30 и C27:С30 ≥ F27:F30. То же самое можно сделать для февраля и марта.
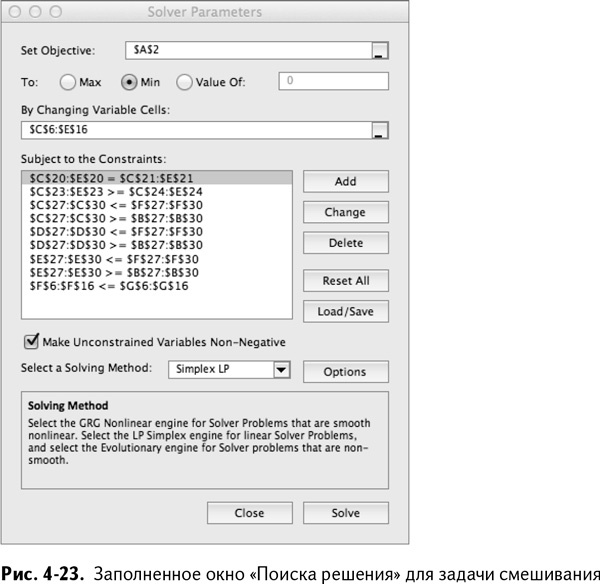
После того, как вы добавили все эти ограничения, убедитесь, что установлен метод решения «Поиск решения линейных задач симплекс-методом». Окончательная таблица изображена на рис. 4-23.
Запустив «Поиск решения», вы находите оптимальную стоимость закупок – $1,23 миллиона (рис. 4-24). Обратите внимание, что заказ флоридской «валенсии» проходит по нижней границе условия. Очевидно, эта сделка – не лучший вариант, но приходится смириться. Второй по популярности сорт – это «верна» из Мексики, которая чертовски дешева, но ровно настолько же ужасна. Модель балансирует этот горький и кислый сок смесью из «белладонны», «биондо коммуне» и «гарднера», которые мягче, слаще и дают лучший цвет. Миленько!
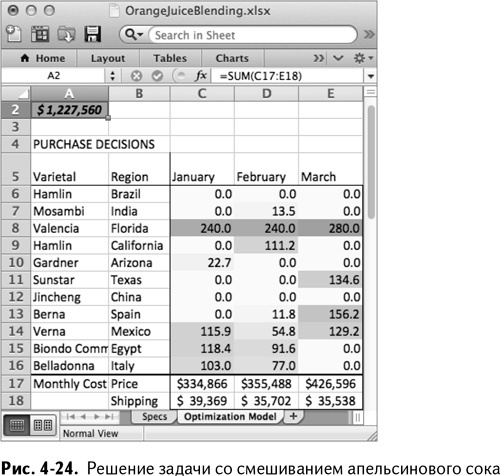
Снижаем стандарты
В полном восторге вы несете ваш план оптимального смешивания своему начальнику, мистеру Лэндингсли III. Вы объясняете, как пришли к такому варианту. Он разглядывает бумагу с подозрением. И даже, несмотря на ваши заверения в оптимальности плана, требует урезать стоимость еще на 5 %. И объясняет свою очевидно бессмысленную позицию спортивными аналогиями «играй всеми нападающими» и «выдай мне 110 %».
Со спортивными аналогиями нет смысла спорить. Если именно $1 170 000 – подходящая цифра, то пусть так и будет. Вы объясняете, что достичь этого с имеющимися условиями качества невозможно, а он ворчит и говорит вам, что ваша задача – «немного прогнуть реальность».
Хммм…
Вы возвращаетесь к своей таблице взволнованным.
Как можно получить смесь лучше за $1 170 000?
После разговора по душам с мистером Лэндингсли вы понимаете: стоимость – больше не цель. Это теперь условие! А что же цель?
Ваша новая цель, порожденная ворчанием начальника, формулируется как понижение качества ради снижения стоимости. А способ ее достигнуть – это вставка переменной решения в модель с тем, чтобы снизить ограничения качества.
Что ж, вперед – копируем лист Optimization Model в чистую таблицу под названием Relaxed Quality. Эта задача не потребует больших изменений.
Посидите минутку и подумайте, как и что можно изменить, чтобы модель соответствовала новым послаблениям в цели и цене. Не вставайте, пока не заболит голова!
Первое, что вы должны сделать, – это внести $1 170 000 как ценовое ограничение в ячейку В2, прямо за старой целевой ячейкой. Также скопируйте старые минимальные и максимальные значения вкуса и цвета в столбцы H и I соответственно. А в строки 27–30 столбца G добавьте новую переменную решения под названием %Relaxed.
Теперь подумайте, как вы можете использовать снижение значения отношения Брикс/кислотность в ячейке G27, чтобы понизить ограничение в 11,5. Текущее значение этого параметра варьируется от 11,5 до 12,5, то есть разница равна 1. Поэтому расширение этого «коридора» на 10 % даст нам минимальное значение в 11,4.
Следуя этому подходу, замените минимум в В27 на эту формулу:
=H27-G27*(I27-H27)
Берем старый минимум, находящийся теперь в Н27, и применяем к нему процентное послабление, умноженное на расстояние от старого максимума до старого минимума (127 минус Н27). Можете скопировать эту формулу вниз до строки 30. Точно так же примените новый максимум с послаблением в столбце F.
Что касается целевой функции, возьмите среднее из решений с послаблением из G27:G30. Поместив этот расчет в ячейку D2, получаем новый лист, который выглядит как рис. 4-25.
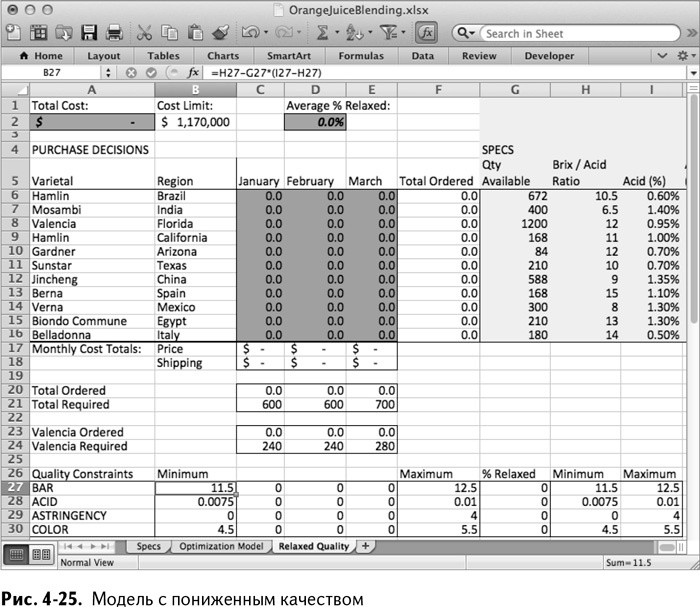
Откройте «Поиск решения» и замените целевую функцию на минимизацию среднего послабления качественных ограничений из ячейки D2. Также вам нужно добавить G27:G30 в список переменных решения и установить стоимость в А2 меньшей или равной ограничению в В2. Эти новые настройки показаны на рис. 4-26.
Обобщим сделанное: мы превратили прошлую целевую стоимость в ограничение с верхней границей. Также мы превратили жесткие ограничения качества в мягкие, которые могут быть ослаблены изменением G27:G30. Ваша цель в D2 – минимизировать среднее снижение качества согласно характеристикам. Нажмите «Выполнить».
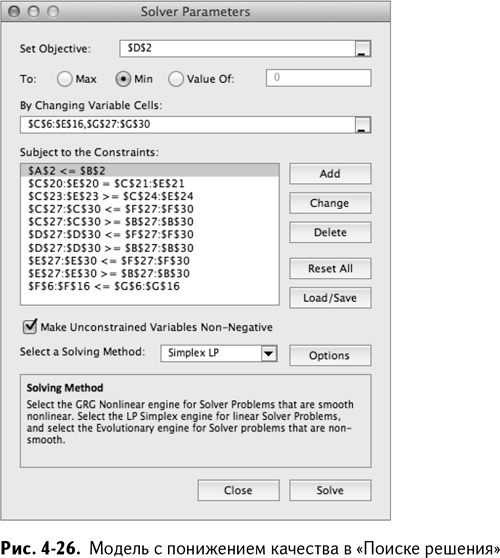
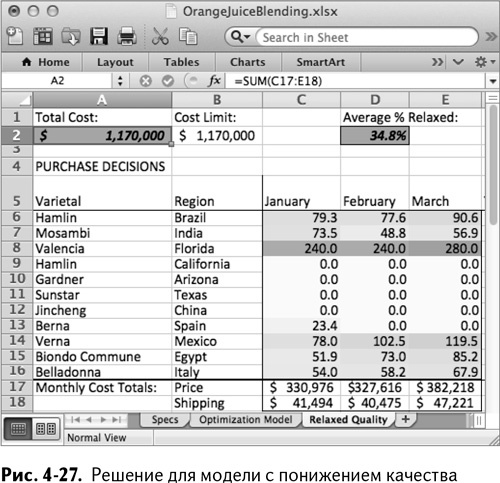
Excel находит решение: со средним снижением каждого ограничения на 35 % возможно достижение результата в рамках указанного ценового ограничения, как показано на рис. 4-27.
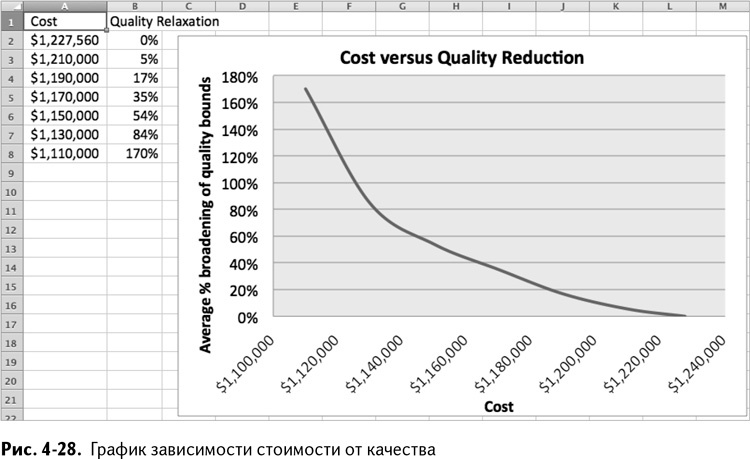
Теперь, когда есть готовая модель, единственное, что вы можете сделать еще – это предоставить мистеру Лэндингсли больше информации, чем он просил. Известно, что при стоимости $1,23 миллиона понижение качества составит 0 %, так почему же не рассчитать пошагово понижение стоимости с максимальным шагом, предположим, в 20 или около того, и не посмотреть, к чему приводит снижение качества? При $1,21 миллионах это 5 %, при $1,19 – уже 17 % и т. д., включая 35, 54, 84 и 170 %. Если попытаться опуститься ниже $1 миллиона, модель становится непригодна.
Создав новый лист под названием Frontier, вы можете вставить в него все решения и создать для них графики, чтобы проиллюстрировать зависимость качества от стоимости (рис. 4-28). Чтобы создать график, как на рис. 4-28, просто выделите два столбца с данными на листе Frontier и вставьте диаграмму «График» со сглаживанием из меню «Диаграммы» (в главе 1 более подробно описан процесс вставки диаграмм).
Удаление дохлых белок: правило минимакс
Взглянув на решение с понижением качества при ограничении стоимости в $1,17 миллиона, можно увидеть потенциальную проблему. Конечно, среднее послабление по цвету и вкусу составляет 35 % от прежних рамок, но для цвета это уже 80 %, а для отношения Брикс/кислотность – 51 %. Усреднение скрывает величину этого отклонения.
В данной ситуации необходимо минимизировать максимальное снижение всех четырех качественных ограничений. Такая проблема называется проблемой минимакса, потому что минимизируется максимум (это слово забавно повторять быстро-быстро: минимакс, минимакс, минимакс…).
Как достичь «поголовной» минимизации? Если сделать целевой функцией MAX(G27:G30)/МАКС(G27:G30), она будет нелинейной. Можно попытаться использовать эволюционный алгоритм, но компьютер будет обсчитывать его целую вечность. Однако существует линейный способ решения этой нелинейной задачи.
Для начала скопируйте модель со сниженными ограничениями на новый лист и назовите его Minimax Relaxed Quality.
А теперь скажите, кому из вас случалось находить дохлых зверушек и избавляться от них? Прошлым летом на моем жарком, как чистилище, чердаке здесь, в Атланте, подохла белка и запах от нее всполошил всю округу.
Как я избавился от этой белки?
Я отказался трогать ее и вообще иметь с ней дело непосредственно.
Я выгреб ее с чердака лопатой, прижав сверху рукояткой от швабры. Это было похоже на работу гигантскими щипцами для салата или палочками для еды. В конечном итоге результат оказался точно таким же, как если бы я вытащил ее оттуда голыми руками, но чувствовал я себя не так мерзко.
Вы можете справиться с расчетом MAX(G27:G30)/МАКС(G27:G30) точно так же, как я справился с той белкой. Так как вам больше не нужно среднее значение G27:G30, вы можете стереть целевую функцию из D2. В этой ячейке вы вычислите функцию MAX(), но пока оставьте ее пустой. Нужно найти значение функции, не имея с ней дела напрямую.
Вот как можно это сделать:
• Назначить целевую ячейку D2 переменной решения, чтобы алгоритм мог совершать над ней все необходимые действия. Не забывайте: если вы задали модели цель – минимизировать, симплексный алгоритм будет пытаться уменьшить значение в этой ячейке насколько это возможно.
• С помощью окна «Добавить условие» поставить следующее условие: такое, что G27:G30 должны быть меньше или равны D2. D2 нужно поставить в правую часть неравенства, чтобы разрешить Excel использовать разное число ячеек (4 ячейки из столбца G слева и одна справа, ограничивающая неравенство сверху). Единственный раз в этой главе вы можете использовать разное количество ячеек в неравенстве ограничения, потому что Excel умеет работать с вариантом, когда правая часть неравенства выражена единственной ячейкой.
Отлично, и что же мы только что сделали?
Симплексный алгоритм будет пытаться приблизить D2 к 0 как целевую функцию модели, в то время как ограничения по вкусу и цвету будут пытаться увеличить ее насколько возможно, чтобы получить пригодную для работы смесь. Где же остановится значение D2? Самое меньшее из возможных значений – максимальный процент из четырех сниженных в промежутке от G27 до G30.
Когда целевая функция достигнет этого максимума, «Поиску решения» останется только тянуть его вниз. Как в случае с белкой, ограничения – это лопата под белкой, а минимизация – это ручка от швабры, прижимающая ее сверху. Вот мы и получили термин «минимакс». Неплохо, да? Или отвратительно… зависит от вашего отношения к дохлым белкам.
И теперь, когда вы оставили пустой ячейку D2, «Поиск решения» будет настроен следующим образом (делаем D2 переменной и добавляем G27:G30 ≤ D2), как на рис. 4-29.
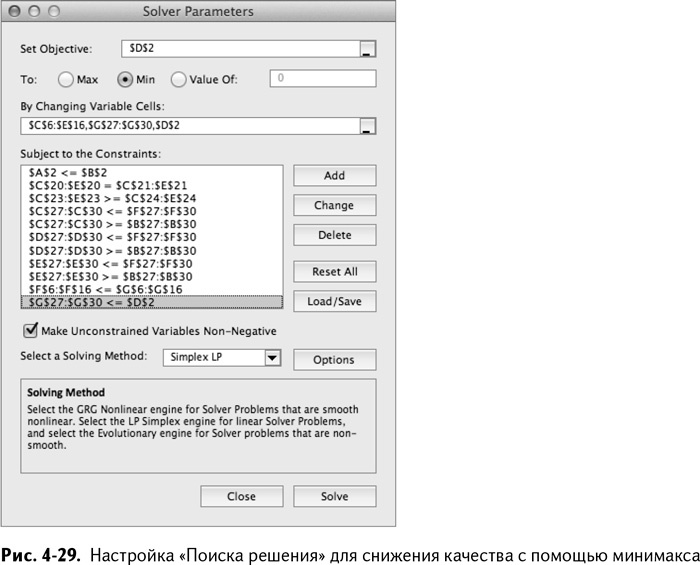
«Поиск решения» приводит нас к понижению качества на 58,7 %, что, хотя и больше, чем средний процент 34,8 из прошлой модели, но гораздо лучше случая с ухудшением цвета на 84 %.
«Если… то» и ограничение «Большого М»
Теперь, когда вы достаточно близко познакомились со стандартным линейным моделированием, можно добавить немного целых чисел. К вашей неимоверной радости, мистер Лэндингсли III внезапно утвердил ваш первоначальный план, но, когда вы приносите его в отдел снабжения, сотрудников перекашивает.
Они отказываются поставлять сок в каком бы то ни было месяце от более чем четырех поставщиков. Видимо, слишком много бумажной работы.
Хорошо, как же это описать внутри модели?
Перед тем как продолжить, подумайте минутку о том, какие могут потребоваться изменения.
Начнем с копирования первоначальной модели оптимизации с листа Optimization Model на новый лист, который назовем Optimization Model (Limit 4).
Теперь, вне зависимости от количества закупаемого сока у поставщика, будь то 1000 галлонов или 1 000 000, считаем это заказом от одного поставщика. Другими словами, вам нужно щелкнуть счетчиком, если вы заказали у поставщика хоть каплю.
В целочисленном программировании этот счетчик – бинарная переменная решения, являющаяся на деле ячейкой, которая может принимать лишь два значения – 0 и 1.
Все, что вам нужно сделать – это определить диапазон такого же размера, что и переменные заказа, а состоять он будет из 0 и 1, где 1 означает существующий заказ.
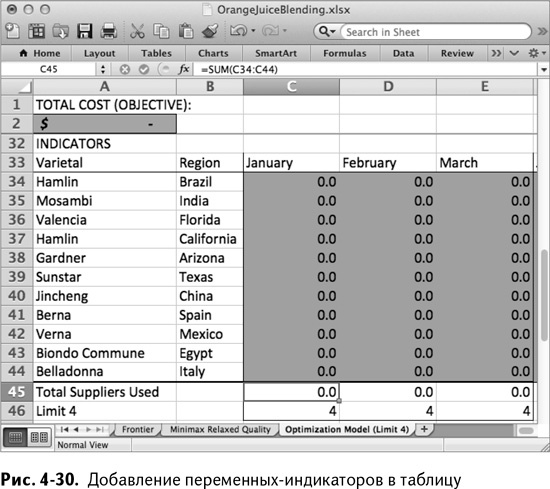
Эти переменные можно вставить в промежуток С34:Е44. Теперь, предполагая, что они примут значение 1, если заказ сделан, можно просуммировать каждый столбец в строке 45 и убедиться, что сумма меньше ограничения 4, которое можно установить в строке 46. Получившаяся таблица показана на рис. 4-30.
Но есть здесь одна загвоздка. Вы не можете использовать функцию IF/ЕСЛИ, которая устанавливает индикатор на 1, если количество заказов выше ненулевое. Получится нелинейная функция, из-за которой придется использовать гораздо более медленный эволюционный алгоритм. Для действительно больших задач с условиями «если… то» медленные нелинейные алгоритмы становятся бесполезны. Так что вместо них приходится «включать» использование индикаторов в линейных условиях.
Допустим, вы добавили ограничение: переменная-индикатор бразильского «гамлина» включается, когда создается заказ с использованием условия C34 ≥ C6.
Если предполагать, что С34 – бинарная переменная, то это действие ограничит С6 до максимального значения, равного 1 (что означает 1000 заказанных галлонов).
Таким образом вы моделируете неудобное условие «если… то»: «если заказ сделан, то бинарная переменная включается», используя нечто, в просторечии именуемое условием «большого М». Большое М – это просто число, причем очень большое, названное М. В случае с С34 М должно быть достаточно велико, чтобы вы никогда не заказали бразильского «гамлина» больше, чем М. Ведь вы не можете заказать сока больше доступного объема, верно? И для «гамлина» доступное количество – 672 тысячи галлонов. Пусть это число и будет М.
Теперь вы можете добавить условие, что 672 × C34 ≥ C6. Когда С6 равно нулю, С34 может принять значение 0). А когда С6 больше нуля, то С34 принудительно превращается в 1, чтобы поднять верхнюю границу от 0 до 672.
Чтобы применить это условие в электронной таблице, создайте новый промежуток F34:Н44, где вы будете перемножать индикаторы слева на их относительные доступные количества из промежутка G6:G16. Результат изображен на рис. 4-31.
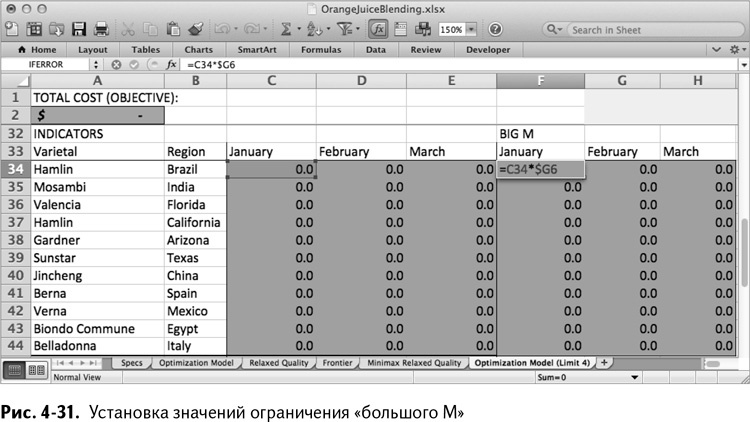
В «Поиске решения» добавьте С34: Е44 в спектр переменных решения. Необходимо сделать их бинарными, что выполняется путем добавления условия bin.
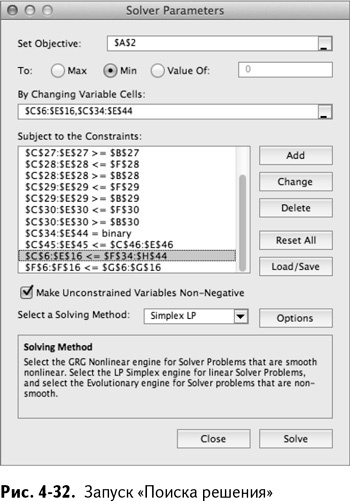
Чтобы заработало ограничение «большого М», установите C6:E16 ≤ F34:H44. Затем проверьте счетчик поставщиков и убедитесь, что он не больше 4 с помощью неравенства C45:E45 ≤ C46:E46. Получившаяся таблица изображена на рис. 4-32.
Нажмите «Выполнить». Вы заметите, что решение задачи требует больше времени из-за добавления бинарных переменных. При использовании бинарных и целочисленных переменных в формулировке «Поиск решения» покажет наиболее подходящее решение из найденных в строке состояния. Если по какой-то причине «Поиск решения» слишком затянул свои поиск, вы всегда можете нажать Escape и увидеть лучшее из найденных решений на данный момент.
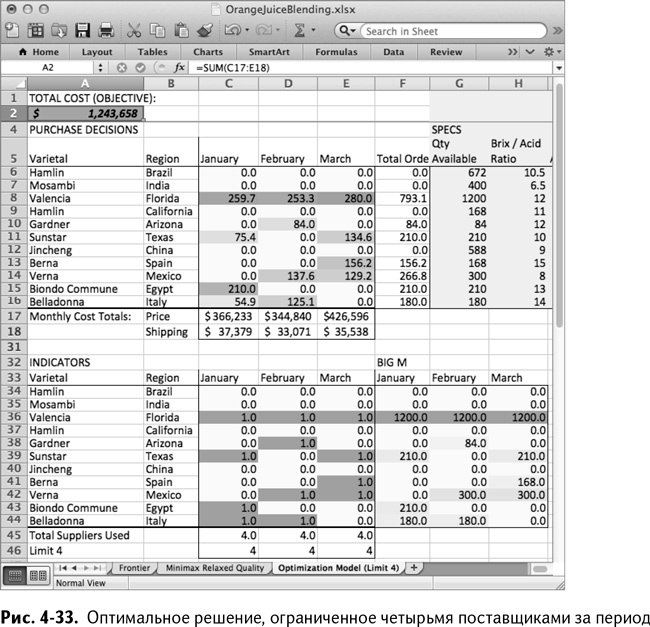
Как показано на рис. 4-33, оптимальное решение для модели, ограниченной четырьмя поставщиками в месяц, – это $1,24 миллиона, примерно на $16 000 больше, чем изначальный оптимум. Вооружившись этим планом, вы можете вернуться в отдел снабжения и спросить их, стоит ли уменьшение их бумажной работы лишних $16 000.
Учитывая таким образом появляющиеся условия, вы реализуете одну из отличительных черт применения оптимизационного моделирования в бизнесе. Помещая значок доллара в результаты своей деятельности, вы можете вынести взвешенное решение вопроса «Стоит ли оно того?».
Вот таким образом устанавливаются ограничения «большого М»; вы еще встретитесь с ними в задаче кластеризации графа в главе 5.
Еще больше переменных: добьем до 11
Перед тем как принять ваш план с ограничением количества поставщиков, вам говорят, что на производстве появились новые «снижатели кислотности». Используя ионообменный механизм и слой цитрата кальция, данная технология способна нейтрализовать 20 % кислоты в соке, протекающем через прибор. Это не только снижает процент кислоты, но и повышает индекс Брикс/кислотность на 25 %.
Но для «снижателя» нужна энергия и расходные материалы стоимостью $20 за 1000 галлонов сока. Не весь сок, поступающий от поставщиков, нужно прогонять через деацидификационный процесс, однако, если поставка по какому-нибудь заказу прогоняется через ионообменник, то должен быть обработан весь ее объем.
Можете ли вы придумать новый план с участием ионообменника для снижения оптимальной стоимости? Подумайте, как изменить задачу. Вам нужно сделать новый набор решений, основываясь на том, когда понижать кислотность, а когда нет. Как эти решения будут взаимодействовать с объемами поставок?
Начните с копирования листа Optimization Model (Limit 4) в новый лист. Назовите его Optimization Model Integer Acid.
Проблема с этим бизнес-правилом заключается в том, что естественный способ его моделирования – нелинейный и придется использовать медленный алгоритм для оптимизации. Можно ввести бинарную переменную, которая бы «включалась» при необходимости понизить кислотность партии. Это значит, что стоимость понижения будет следующей:
понижающий кислотность реагент * объем партии * $20
OPENSOLVER, НЕОБХОДИМЫЙ ДЛЯ EXCEL 2010 И EXCEL 2013
Последние абзацы были сложноваты, но это цветочки по сравнению со следующей моделью.Для этой задачи, пожалуйста, держите наготове заполненную электронную таблицу, чтобы сверяться с ней время от времени. Будет нелегко, но это стоит освоить, особенно если ваш бизнес часто сталкивается со сложными проблемами оптимизации. Если вы не осилите этот раздел, не огорчайтесь: на ваше дальнейшее понимание книги это не повлияет. Но все же советую вам попробовать.Если вы работаете в Excel 2010 или Excel 2013, вам понадобится загрузить и установить OpenSolver (в главе 1 описывается, как это сделать). В противном случае упомянутые версии Excel при решении задачи выдадут ошибку, в которой будет сказано, что оптимизационная модель слишком велика. Чтобы использовать OpenSolver в этой главе, вводите данные для решения как обычно, но когда дело дойдет до решения, используйте кнопку OpenSolver в меню.
Вы не можете перемножить эти две переменные, не переключившись на нелинейный алгоритм. Парадокс заключается в том, что он никогда не отразит все нюансы этой модели. Должен быть способ получше. При работе с линейным программированием не забывайте: мало что нельзя линеаризовать с помощью разумного привлечения дополнительных переменных, манипулировать которыми можно с помощью дополнительных условий и целевой функции, как парой салатных щипцов.
Первое, что вам понадобится – это набор бинарных переменных, которые «включаются», когда вы решаете снизить кислотность партии сока. Часть из них можно поместить в прямоугольник между заказами «валенсии» и ограничениями по качеству (ячейки С26:Е36).
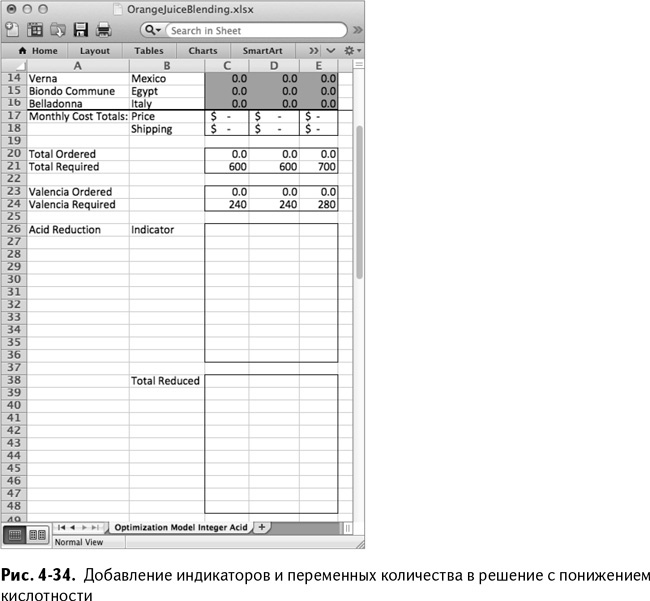
Более того, нельзя использовать произведение «понижающий кислотность реагент × объем партии», поэтому вы создаете новый ряд переменных под индикаторами, которые вам пригодятся для уравнивания данного количества без прямого их участия (типа случая с дохлой белкой). Вставьте эти пустые ячейки в С38:Е48.
Теперь наша электронная таблица содержит два пустых ряда переменных-индикаторов и общего количества сока, пропущенного через ацидоредуктор, как показано на рис. 4-34.
Умножив переменную снижения кислотности на объем заказанных партий, что же мы получим в итоге? Есть несколько вероятных исходов:
• обе переменные – нули, равно как и индикатор и общее количество, соответственно, их произведение также равно 0;
• вы заказали сок, но решили не понижать кислотность – произведение снова 0;
• вы решили понизить кислотность – произведение равно общему количеству сока.
В каждом случае общее возможное количество сока, кислотность которого можно понизить, ограничено индикатором понижения кислотности, умноженным на общее количество сока, доступное для заказа. Если вы не понижаете кислотность, то верхняя граница этого произведения упирается в ноль. Если решаете понизить – эта граница поднимается до максимального объема заказов. Это и есть ограничение «большого М», как и в предыдущем примере.
Для бразильского «гамлина» в таком случае это ограничение может быть рассчитано путем умножения индикатора в ячейке С26 на объем, доступный для заказа, – 672 000 галлонов из ячейки G6. Добавляя этот расчет в ячейку рядом с переменными-индикаторами в G26, вы можете скопировать оставшиеся месяцы и сорта.
Таким образом мы получаем лист, изображенный на рис. 4-35.
С другой стороны, общее возможное количество сока, кислотность которого можно понизить, ограничено объемом, который вы решили заказать, указанным в С6:Е16. Так что теперь у нас есть две верхние границы для этого продукта:
• индикатор понижения кислотности × объем, доступный для заказа;
• заказанное количество.
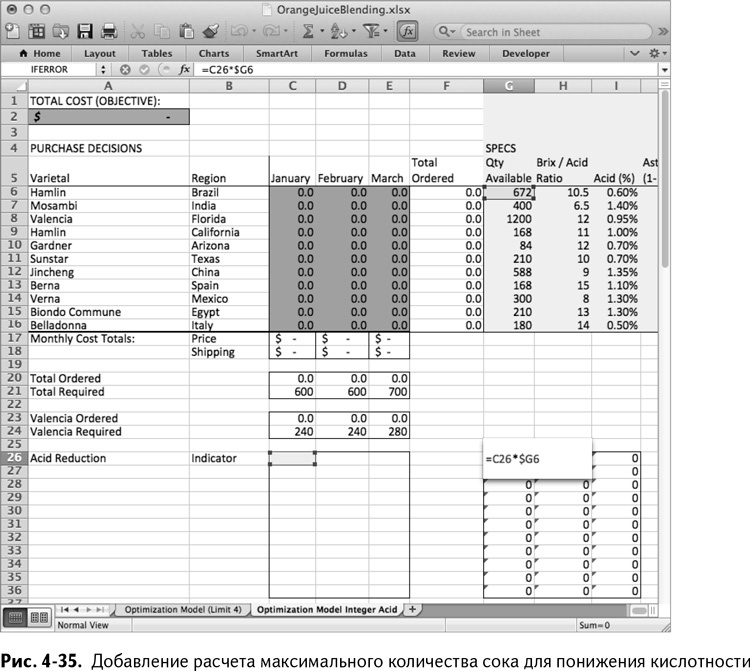
Это – верхние границы для каждой переменной в нелинейном произведении.
Но в таком виде задачу оставлять нельзя. Если вы решаете понизить кислотность партии, вам нужно пропустить через аппарат всю партию. Это значит, что нужно добавить нижнюю границу к двум верхним, чтобы получить количество с пониженной кислотностью в С38:Е48.
Как насчет использования объема заказа в качестве нижней границы? В случае если вы решаете понижать кислотность, прием работает идеально. Нижняя граница выражается объемом заказа, а верхние – объемом заказа и общим количеством, доступным для заказа, умноженным на индикатор понижения кислотности, равный 1. Эти границы определяют объем сока, проходящий через аппарат понижения кислотности, который получается равным полной поставке, что вас полностью устраивает.
А что же произойдет, если вы решите не понижать кислотность партии? В таком случае одна из верхних границ из-за индикатора, равного нулю, сама обращается в ноль, в то время как нижняя граница остается на уровне заказанного количества. В этом случае ненулевое заказанное количество, не подвергающееся деацидификации, становится невозможным.
Хммм…
Вам нужен способ «выключить» эту нижнюю границу в случае, если вы решаете не понижать кислотность.
Вместо того, чтобы обозначить нижнюю границу объемом заказанного сока, давайте попробуем «открыть» ее следующим образом:
заказанное количество – объем, доступный для заказа *
* (1 – индикатор понижения кислотности)
В случае если вы решаете понижать кислотность, эта нижняя граница поднимается до объема заказанной партии. В случае непонижения кислотности эта величина становится меньшей или равной нулю. Условие по-прежнему существует, но во всех случаях бесполезно.
Звучит несколько сомнительно?
Попробую объяснить это на примере. Вы покупаете 40 000 галлонов сока бразильского «гамлина» и решаете понизить его кислотность.
Верхние границы объема, подвергающегося «урезанию», – это объем заказанного сока – 40 и индикатор понижения кислотности, помноженный на доступное количество – 672.
Нижняя граница этого объема равна 40 – 672 × (1–1) = 40. Другими словами, у вас и верхняя и нижняя границы равны 40, так что вы «зажали» этот объем для деацидификации прямо в «индикатор понижения кислотности * заказанный объем», даже не рассчитывая это количество.
Если же решать не понижать кислотность «гамлина», индикатор устанавливается на 0. В этом случае ваши верхние границы равны 40 и 672 × 0 = 0. Нижняя же граница выходит равной 40 – 672 × (1–0) = –632. А так как у вас стоит галочка в поле, делающем все переменные неотрицательными, это значит, что объем «гамлина», кислотность которого вы понижаете, «зажат» между 0 и 0.
Отлично!
Теперь добавьте эту нижнюю границу в таблицу справа от расчета верхней границы. В ячейке К26 напечатайте:
=C6-$G6*(1-C26)
Можете скопировать эту формулу для каждого сорта и месяца, получив в результате таблицу, изображенную на рис. 4-36.
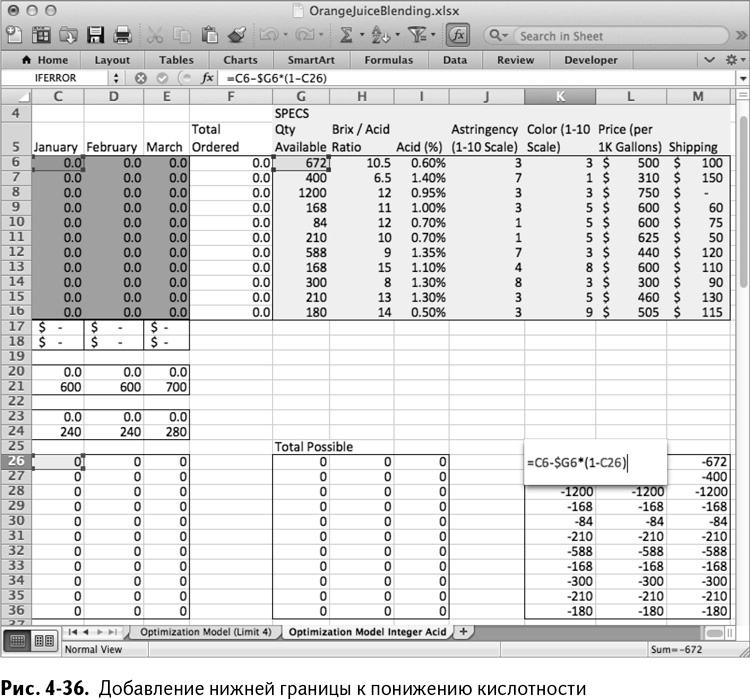
Рядом с разделом Total Reduce вычтите это значение из общего объема заказа в С16:Е16, чтобы получить оставшееся количество сока, не подвергшегося деацидификации. К примеру, в ячейку G38 поместите
=C6–C38
Можете перетащить данные на оставшиеся ячейки этого расчета (как на рис. 4-37).
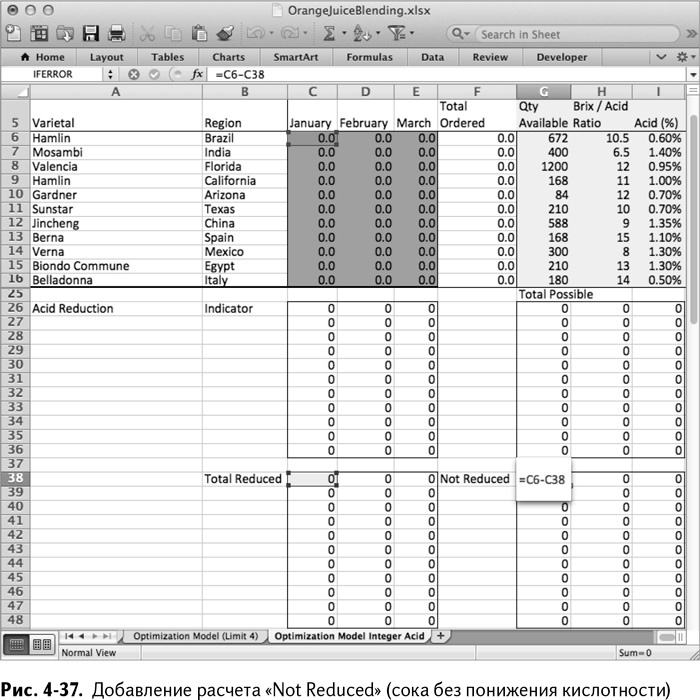
Подытоживая формулировку расчета, вам нужно изменить подсчет стоимости, отношения Брикс/кислотность и процента кислоты. Для расчета стоимости можно просто добавить $20, умноженные на сумму значений Total Reduce (общее количество сока с пониженной кислотностью) за месяц в ячейку Price. К примеру, расчет стоимости за январь в ячейке Price будет выглядеть как
=SUMPRODUCT(C6:C16,$L6:$L16)+20*SUM(C38:C48)
=СУММПРОИЗВ(C6:C16,$L6:$L16)+20*SUM(C38:C48)
что вы с легкостью можете переместить на февраль и март.
Отношение Брикс/кислотность и процент кислоты теперь будут рассчитываться отдельно для Total Reduced (общего количества сока с пониженной кислотностью) и Not Reduced (сока без понижения кислотности). Значения Not Reduced будут пропущены через SUMPRODUCT/СУММПРОИЗВ со своими первоначальными свойствами, в то время как та же самая формула для сока с измененной кислотностью будет изменена на 1,25 и 0,8 соответственно для отношения Брикс/кислотность и кислотности и добавлена к общему среднему за месяц.
К примеру, индекс Брикс/кислотность за январь в С51 может быть рассчитан как
=(SUMPRODUCT(G38:G48,$H6:$H16)+SUMPRODUCT
(C38:C48,$H6:$H16)*1.25)/C21
=(СУММПРОИЗВ(G38:G48,$H6:$H16)+СУММПРОИЗВ
(C38:C48,$H6:$H16)*1.25)/C21
Теперь необходимо модифицировать модель в «Поиске решения». Целевая функция остается прежней (сумма цены и доставки), но переменные решения включают индикаторы понижения кислотности и объемы сока, подлежащие этому понижению, расположенные в С26:Е36 и С38:Е48.
Что касается ограничений, нужно отметить, что С26:Е36 – бинарные. Также, С38:С48 меньше или равны двум верхним границам в С6:Е16 и G26:I36. Еще вам нужно условие для нижней границы: С38:Е48 меньше или равно К26:М36.
Таким образом получается новая модель, изображенная на рис. 4-38.
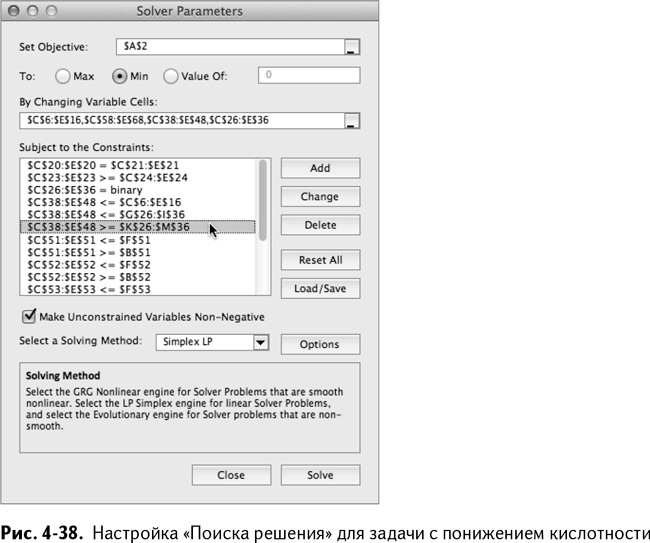
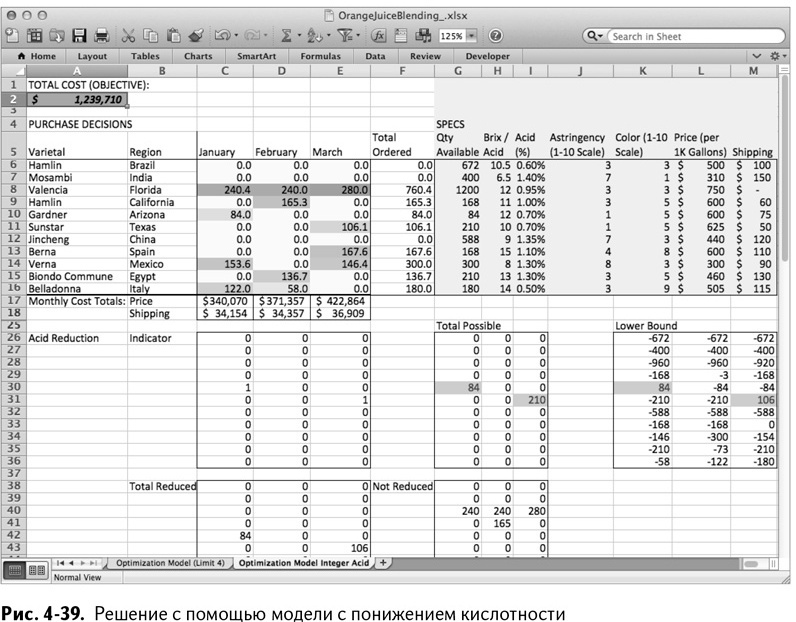
Нажмите «Выполнить» и позвольте ветвям и границам сделать свое дело. В результате получится оптимальное решение, которое окажется на $4000 дешевле, чем предыдущий расчет. Изучив переменные нового решения, вы найдете эти две партии – одна из Аризоны, другая из Техаса – прошедшие через процесс понижения кислотности. Верхние и нижняя границы для этих двух партий точно подходят для того, чтобы поставить произведения переменных на место (рис. 4-39).
Назад: Начнем с простого компромисса
Дальше: Моделируем риски

