Моделируем риски

Книга: Много цифр. Анализ больших данных при помощи Excel

Назад: Свежий, из сада – прямо в стакан… с небольшой остановкой на модель смешивания

Последнее бизнес-правило было тяжеловатым, зато проиллюстрировало, как с помощью модели можно линеаризовать большинство задач бизнеса путем добавления условий и переменных. Неважно, впрочем, насколько просты или сложны были предыдущие задачи – у них есть одна общая черта: они свято чтут вводные данные.

Эта точность не всегда соответствует реальности, в которой вынуждено действовать большинство бизнесменов. Не все партии отвечают заявленным характеристикам, доставка не всегда приходит вовремя, спрос не соответствует прогнозам и т. д. Другими словами, в данных существует вариабельность и риск.

Что же делать с этим риском и как его выразить в оптимизационной модели?

Нормальное распределение данных

В задаче с апельсиновым соком вы пытаетесь смешивать соки, чтобы исключить вариабельность. Резонно предположить, что и продукт, получаемый от поставщиков, также может варьироваться по характеристикам.

Есть вероятность, что доставка апельсинового сока «биондо коммуне» из Египта не будет иметь точного отношения Брикс/кислотность в 13. Реальная цифра наверняка будет немного «плавать» вокруг этого значения. И частенько разница может быть охарактеризована с помощью распределения вероятности.

Говоря простым языком, распределение вероятности дает процент возможности каждого исхода некоторой ситуации, и все вероятности в сумме дадут 1. Самое, наверное, известное и широко используемое распределение – это нормальное распределение, иначе называемое «колоколообразной кривой». Секрет популярности этой кривой заключается в том, что при наличии ряда независимых, комплексных, реальных факторов, наложенных один на другой, получаются случайные данные, которые часто распределяются нормальным, или колоколообразным, образом. Это называется центральной предельной теоремой.

Проиллюстрирую вышесказанное небольшим экспериментом. Достаньте ваш мобильный и запишите последние четыре цифры каждого сохраненного в нем номера. Цифра 1, скорее всего, будет равномерно распределена между 0 и 9, то есть каждая из этих цифр будет встречаться примерно одинаковое количество раз. То же можно отнести и к цифрам 2, 3 и 4.

А теперь возьмем эти четыре «случайные переменные» и сложим их. Наименьшее число, которое вы можете получить, это 0 (0 + 0 + 0 + 0). Наибольшее – 36 (9 + 9 + 9 + 9). Тот есть существует только один способ получить 0 и 36. Есть четыре способа получить 1 и четыре – получить 35, но уйма способов получения 20. Если вы проверите это утверждение на достаточном количестве телефонных номеров и выведете диаграмму различных сумм, то в итоге получится колоколообразная кривая, как на рис. 4-40 (для построения этой диаграммы я использовал 1000 телефонных номеров – да, я ровно настолько популярен).

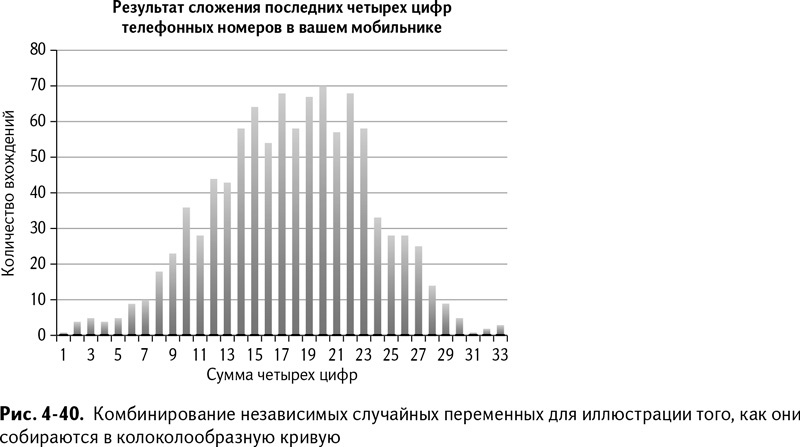
Интегральная функция распределения

Есть другой способ, который называется интегральное (или кумулятивное) распределение. Функция интегрального распределения дает вероятность исхода, меньшую или равную определенной величине.

В примере с данными из мобильного только 12 % случаев меньше или равны 10, в то время как 100 % меньше или равны 36 (так как это наибольшее возможное значение). Интегральное распределение показано на рис. 4-41.

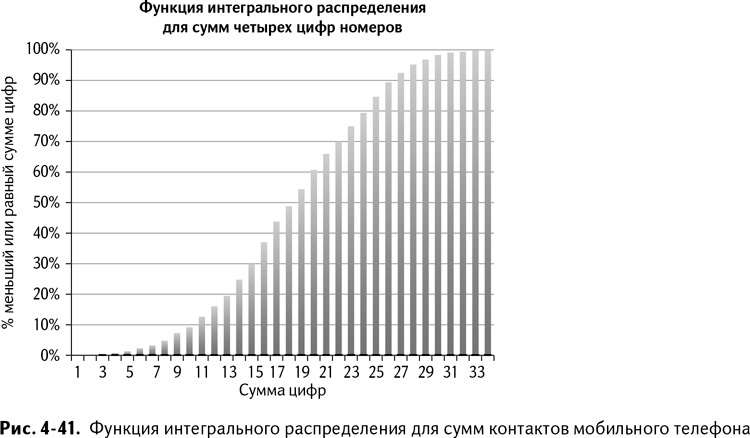
У этого распределения есть одно замечательное свойство – его можно читать задом наперед и генерировать примеры из представления.

К примеру, случайное число из этого распределения сумм последних четырех цифр номеров в записной книжке может составить случайный процент от 0 до 100. Допустим, 61 %. Смотрим на вертикальную ось распределения – 61 % пересекается с 19 на горизонтальной оси. Так можно делать снова и снова, генерируя случайные числа с помощью распределения.

Обычное интегральное распределение может быть описано двумя числами: средним значением и среднеквадратичным отклонением. Среднее – не что иное, как центр распределения. Среднеквадратичное отклонение же измеряет вариабельность, или рассеяние, колоколообразной кривой вокруг среднего.

Скажем, в случае с соком из Египта среднее значение отношения Брикс/кислотность будет 13, а среднеквадратичное отклонение – 0,9. В данном примере 13 – это центр распределения вероятности, а 68 % заказов будут в пределах +/– 0,9 от 13,95 % будут в пределах двух среднеквадратичных отклонений (+/– 1,8), а 99,7 % будут находиться в пределах трех среднеквадратичных отклонений (+/– 2,7). Это еще называется правилом «68–95–99,7».

Другими словами, весьма вероятно, что из Египта вы получите сок с отношением Брикс/кислотность = 13,5, но получить партию с этим показателем = 10, – очень маловероятно.

Расчет выборочного среднего

и среднеквадратичного отклонения

Тех из вас, кто раньше не сталкивался с расчетом среднеквадратичного отклонения и заинтригован, я обрадую: все очень просто.

На рис. 4-42 показаны 11 последних заказов сока «биондо коммуне» из Египта и их отношение Брикс/кислотность в столбце В. Выборочное среднее для этих значений будет равно 13, как и написано в таблице характеристик.

Выборочная оценка среднеквадратичного отклонения – это просто квадратный корень из среднеквадратичной погрешности. Под словом «погрешность» я понимаю отклонение каждой партии от предполагаемого значения 13.

В столбце С рис. 4-42 вы можете увидеть расчет погрешности, а в столбце D – квадрат погрешности. Среднеквадратичная погрешность – это AVERAGE(D2:D12)/СРЗНАЧ(D2:D12), которая оказывается равной 0,77. И тогда квадратный корень из среднеквадратичной погрешности равен 0,88.

На практике во время расчета среднеквадратичного отклонения для небольшого количества партий можно получить более точную оценку, если сложить квадраты погрешностей и разделить их поочередно на число, на 1 меньшее, чем общее количество заказов (в нашем случае – 10 вместо 11).

Если вы примените такой подход, стандартное отклонение становится равным 0,92, как показано на рис. 4-42.

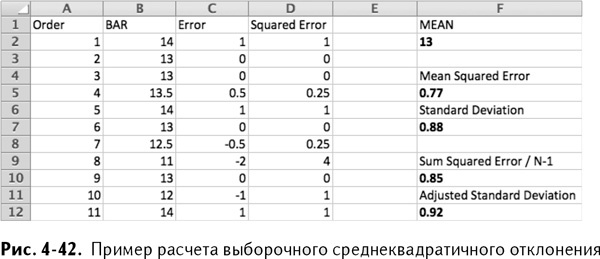
Генерируем сценарии из среднеквадратичных отклонений в задаче смешивания

Заметка

Точно так же, как в предыдущем разделе, пользователям Excel 2010 и Excel 2013 понадобится помощь OpenSolver. Ставьте задачу, формируйте решение, как обычно, и используйте кнопку выполнения OpenSolver в меню, когда дело дойдет до решения. Более подробно OpenSolver описан в главе 1.

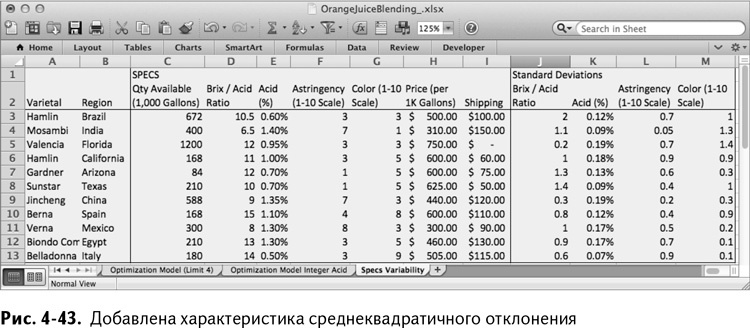
Представьте, что вместо таблицы характеристик вы получили среднеквадратичные отклонения вместе со всеми характеристиками в таблице под названием Specs Variability, показанной на рис. 4-43. Ваша цель – придумать план смешивания стоимостью меньше $1,25 миллиона, который наилучшим образом соответствует ожиданиям по качеству в свете вариабельности поставок.

Можете создать копию первоначальной таблицы Minimax Relaxed Quality и назвать ее Robust Optimization Model, а новые среднеквадратичные отклонения поместить в N6:Q16 в соответствии со старыми характеристиками.

Поместили. А что теперь?

Используйте среднее и среднеквадратичное отклонение характеристик, чтобы применить имитационное моделирование по методу Монте-Карло. В этом методе вместо включения распределения в модель напрямую каким-либо образом берется образец распределения, создаются сценарии или обсчитывается каждый набор образцов, после чего они включаются в модель.

Сценарий – это один из возможных ответов на вопрос: «Если это – распределения, основанные на статистике, на что же будет похож настоящий заказ?» Чтобы нарисовать такой сценарий, нужно посмотреть на функцию распределения – охарактеризованную средним и среднеквадратичным отклонением – наоборот, как описывалось ранее с рисунком 4-41.

Формула Excel для прочтения функции распределения задом наперед (или в «инвертированном виде») называется NORMINV/НОРМОБР.

Начнем генерировать сценарий в столбце В: с 33-й строки все уже заполнено. Можете назвать это Scenario 1.

В В34:В44 у вас будет настоящий сценарий для значения отношения Брикс/кислотность по всем поставщикам. В В34 сгенерируйте случайное значение для бразильского «гамлина» с учетом того, что отношение Брикс/кислотность составит 10,5 (Н6), а среднеквадратичное отклонение – 2 (N6), используя формулу NORMINV/НОРМОБР:

=NORMINV(RAND(),$H6,$N6)

=НОРМОБР(RAND(),$H6,$N6)

Вы вводите случайное число от 0 до 100 % в формулу NORMINV/НОРМОБР, а также среднее и среднеквадратичное отклонения, и в итоге получаете случайное значение отношения Брикс/кислотность. Растянем эту формулу до В44.

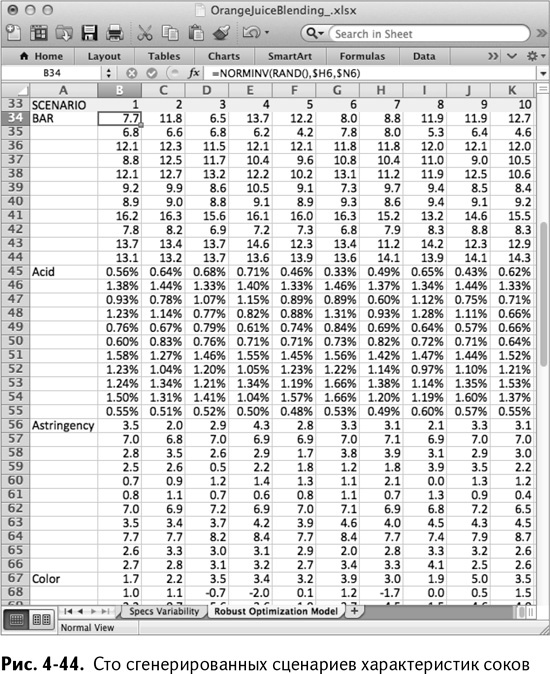
Начиная с В45, можно делать то же самое с кислотностью, затем терпкостью и, наконец, с цветом. Область В34:В77 теперь содержит единый сценарий, случайно выведенный из отклонений. Растягивая его на все столбцы до CW (фиксируйте абсолютные ссылки, позволяющие это сделать), можно сгенерировать сто таких сценариев со случайными характеристиками. «Поиск решения» не понимает их, пока они не остаются в нелинейной форме, поэтому скопируйте их и вставьте в их же начала, но только в качестве обычных значений. Теперь сценарии существуют в виде закрепленных данных.

Эти горы данных для сценариев в В34:CW77 изображены на рис. 4-44.

Устанавливаем ограничения для сценариев

Теперь нужно найти решение, которое менее всего снижает границы качества в каждом из сгенерированных вами сценариев. Фактически это решение, защищающее продукт.

Итак, под первым сценарием в ячейке В79 рассчитайте отношение Брикс/кислотность в январе:

=SUMPRODUCT($C$6:$C$16,B34:B44)/$C$21

=СУММПРОИЗВ($C$6:$C$16,B34:B44)/$C$21

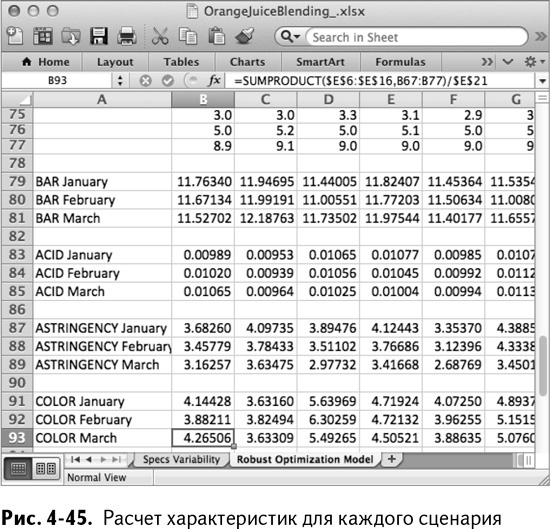
То же самое можно сделать и для февраля и марта в строках 80 и 81, а затем распространить весь расчет до самого столбца CW, чтобы получить значение этого отношения для каждого сценария.

В итоге вы получаете расчеты для каждого сценария, показанные на рис. 4-45.

Дальнейшая настройка модели не так уж сложна. Ставим верхнюю границу стоимости, равную $1,25 миллиона, в В2. Продолжаем минимизировать D2 – снижение качества – с настройками минимакса. Все, что нужно – это поместить во все сценарии границы качества, а не просто ожидаемые значения характеристик.

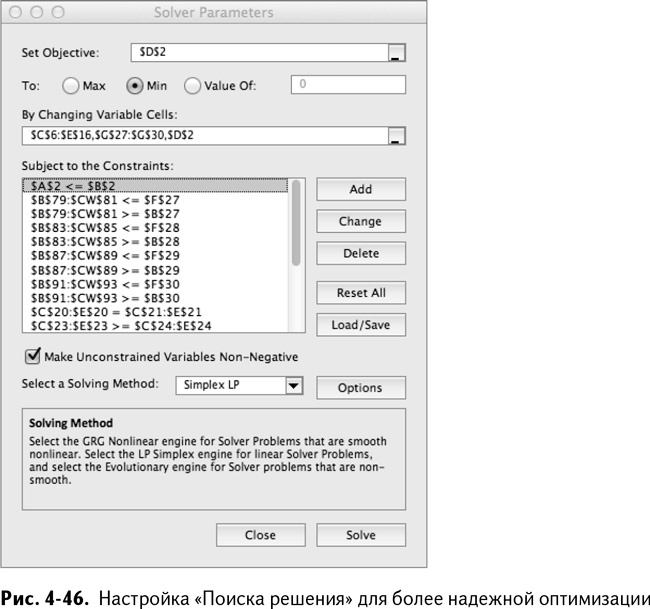
Таким образом, в отношение Брикс/кислотность вы добавляете условие B79:CW81 ≥ B27 и ≤ F27, затем проделываете то же самое с кислотностью, вяжущей составляющей вкуса и цветом, получая в итоге формулировку, показанную на рис. 4-46.

Нажмите «Выполнить». Решение найдется довольно быстро. Если вы генерировали случайные значения сами, а не использовали те, что находятся в файле для загрузки, оно может отличаться. Для моей сотни сценариев наилучшим показателем, который мне удалось получить, является изменение качества на 133 % с сохранением стоимости менее $1,25 миллиона.

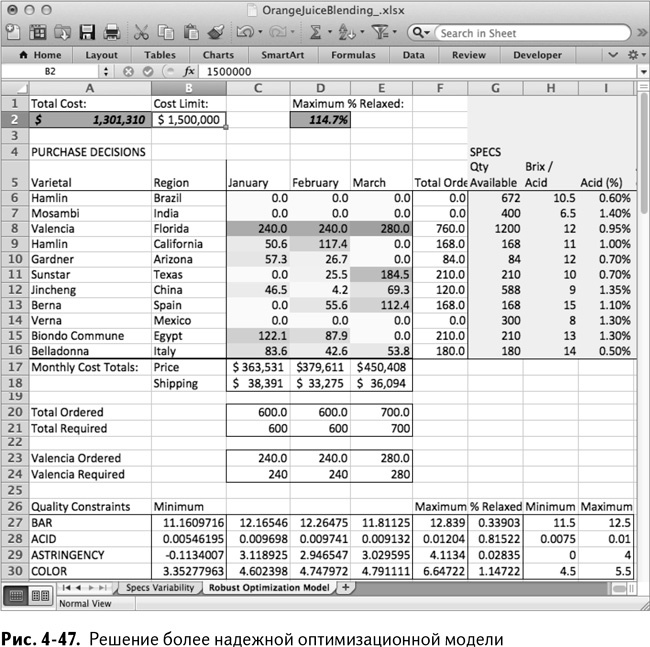
Ради смеха можно поднять верхнюю границу стоимости до $1,5 миллиона и решить все снова. Получится изменение на 144 %, причем цена будет сильно недотягивать до верхней границы, оставаясь близкой к $1,3 миллиона. Видимо, увеличение стоимости выше этого значения не дает большого резерва для улучшения качества (решение на рис. 4-47).

Ну, вот и все! Теперь у вас есть баланс стоимости и качества, удовлетворяющий условиям даже в случайных, близких к реальности ситуациях.

Назад: Свежий, из сада – прямо в стакан… с небольшой остановкой на модель смешивания

Дальше: Подытожим