Начнем с простого компромисса

Книга: Много цифр. Анализ больших данных при помощи Excel

Назад: Зачем ученым, работающим с данными, нужна оптимизация?

Дальше: Свежий, из сада – прямо в стакан… с небольшой остановкой на модель смешивания

Этот раздел я начну с двух любимых «пунктиков» экономистов – пушек и масла.

1941 год, вы десантированы за линию фронта под именем Жереми (или Амелин) Гальендо, хозяина французской молочной фермы.

Ваша работа днем: дойка коров и продажа сладкого сливочного масла местному населению.

Ваша работа ночью: сборка и продажа автоматов французскому Сопротивлению.

Ваша жизнь сложна и полна опасности. Вы начисто отрезаны от штаба и вам остается лишь работать на ферме, стараясь не попасться на «крючок» нацистам. Денег в вашем бюджете хватает только, чтобы свести концы с концами, собирая автоматы и сбивая масло. Вы должны продержаться до конца войны. Нельзя потерять ферму, ведь это – прикрытие!

После долгих раздумий о своем нелегком положении, вы смогли охарактеризовать его тремя составляющими.

• Цель. Вы получаете $195 (ой, простите, франков, хотя, честно говоря, мой Excel настроен на доллары, и я не собираюсь менять настройки ради этого примера) за каждый автомат, который продаете своему доверенному лицу – Пьеру. Вы получаете $150 за каждую бочку проданного на рынке масла. Вам нужно получать как можно больший доход, чтобы окупать ферму.

• Задача. Вам необходимо выяснить, сколько автоматов и сколько масла вам нужно продать за месяц, чтобы получить максимальную прибыль.

• Условия и ограничения. Производство одной бочки масла обходится вам в $100, а сборка одного автомата – в $150. Ваш месячный бюджет на производство новой продукции – $1800. Вам приходится хранить эту продукцию в своем 21-кубометровом подвале. Автомат занимает половину кубометра, бочка масла занимает полтора кубометра. Ни автоматы, ни масло невозможно хранить в другом месте: первые заметят нацисты, а второе испортится.

Представим проблему в виде политопа

Проблема, представленная подобным образом, называется линейной программой. Линейная программа определяется как набор решений, необходимый для оптимизации объекта в свете некоторых условий, где и объект, и условия линейны. Линейность в данном случае означает, что каждое уравнение будет лишь добавлять решения, вычитать их, умножать на константы или все упомянутое вместе.

В линейном программировании вы не можете применять для решения нелинейные функции, к которым, к примеру, относятся:

• перемножение решений (автоматы, помноженные на масло, неприменимы);

• применение логических циклов, таких как ЕСЛИ («Если хранить в подвале только масло, то можно сделать небольшое отверстие в полу, и тогда полезный объем подвала увеличится до 22 кубических метров»).

Как вы увидите в дальнейшем, ограничения лишь стимулируют творческий подход.

Вернемся к нашей проблеме. Начнем с графического определения «области допустимых значений» для этой проблемы. Допустимые значения – это множество возможных решений. Можно ли не производить ни масла, ни автоматов? Конечно. Бездействие не увеличит прибыль, но теоретически оно возможно. Можете ли вы делать по 100 автоматов и 1000 бочек масла в месяц? Нет, с данным бюджетом и в вашем тесном подвале это невозможно.

Так с чего же начать построение графика? Ну, во-первых, нельзя производить отрицательные количества автоматов и масла. Мы же не занимаемся теоретической физикой. Поэтому нам нужен только первый квадрант координатной плоскости.

В терминах бюджета, при цене $150 за штуку вы можете собирать по 12 автоматов в месяц, используя бюджет в $1800. А по цене $100 за бочку вы можете произвести 18 бочек масла.

И если изобразить бюджетное ограничение как линию на графике, то эта линия пойдет аккурат через 12 автоматов и 18 бочек масла. Как показано на рис. 4–1, область допустимых значений в данном случае представляет собой треугольник положительных чисел, согласно которому вы можете произвести максимум 12 автоматов или 18 бочек масла в месяц, или некоторую линейную комбинацию их меньших значений.

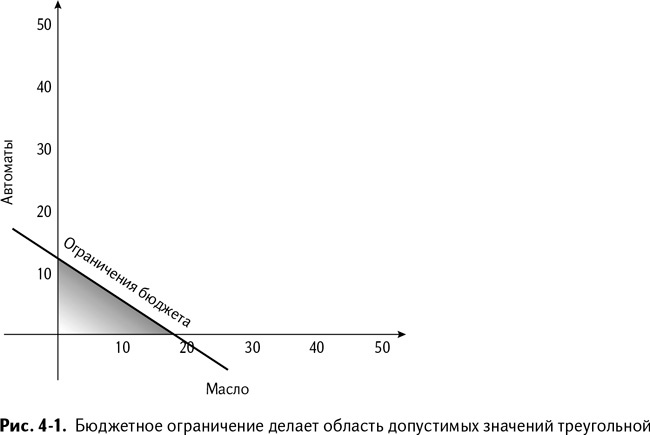
Для этого треугольника есть более общее название – политоп. Политоп – это не более чем геометрическая фигура с плоскими сторонами. Наверняка вы слышали термин «полигон». Полигон – это просто двумерный политоп. Если у вас в обручальном кольце есть внушительный камень – бах! бриллиант, радуйтесь: это политоп.

Во всех линейных программах области допустимых значений могут быть выражены в качестве политопов. Некоторые алгоритмы, как вы не замедлите убедиться, используют этот факт для ускоренного решения линейных проблем.

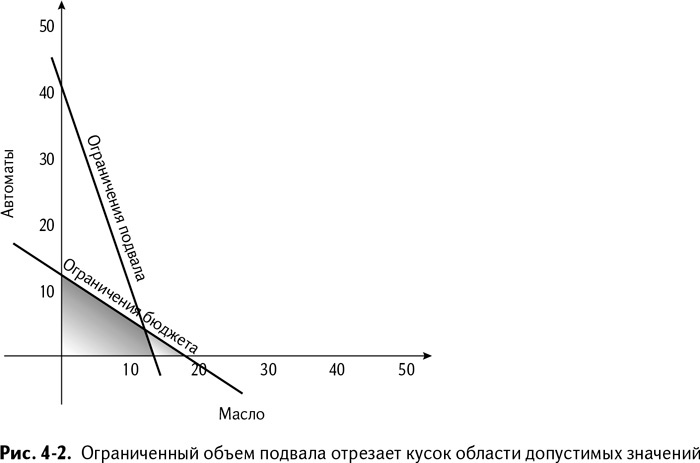
Но не отвлекаемся от масла и оружия! Пришло время рассмотреть второе ограничительное условие – подвал. Если бы вы производили только автоматы, их можно было бы уместить там 42 штуки. С другой стороны, в такой подвал может уместиться не более 14 бочек масла. Добавив это ограничение к политопу, мы отсекаем часть области допустимых значений, как показано на рис. 4–2.

Решение путем сдвигания линии уровня функции

После определения области допустимых значений у вас может возникнуть вопрос: «И где же в этой области находится идеальное соотношение автоматов и масла?»

Чтобы на него ответить, введем в задачу такое понятие, как линия уровня функции. Линией уровня для вашей оптимизационной модели будет та область, в которой все значения приносят одинаковый доход.

Так как функция вашей прибыли – это $150 × масло + $195 × автомат, каждая линия ее уровня может быть определена как прямая $150 × масло + $195 × автомат = С, где С – фиксированная величина прибыли.

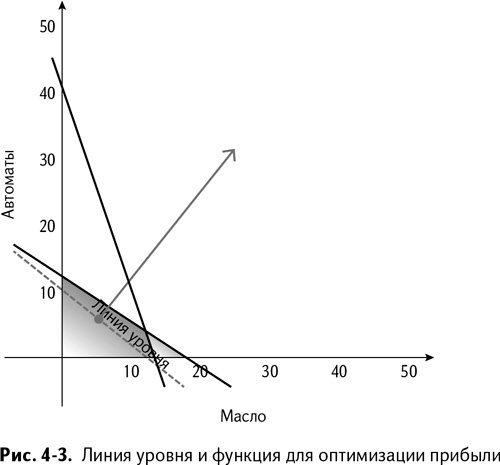
Рассмотрим случай, где С = $1950. Для линии уровня $150 × масло + $195 × автомат = $1950 обе точки – (0,10) и (13,0) – принадлежат ей, как и любая комбинация из масла и автоматов, при которой $150 × масло + $195 × автомат равняется $1950. Эта линия уровня изображена на рис. 4–3.

Используя идею линии уровня, можно начать думать над проблемой максимизации прибыли, сдвигая линию уровня по направлению нарастания прибыли (это направление будет перпендикулярно самой линии) до последнего возможного значения, находящегося в области допустимых значений.

На рис. 4–3 линия уровня нарисована пунктиром, а стрелка, отходящая от нее, представляет собой целевую функцию.

Симплекс-метод: все по углам

Повторяю: если вы хотите знать, какие значения из области допустимых значений оптимальны – просто сдвиньте линию уровня функции в направлении нарастания дохода. Прямо на границе, где линия вот-вот выйдет из области политопа, и находятся эти точки. И вот один замечательный факт: одна из этих оптимальных точек на границе всегда будет лежать в углу политопа.

Проверьте это по рис. 4–3. Положите карандаш на линию уровня и сдвигайте его вверх и вправо, в направлении увеличения дохода. Видите, как она выходит из политопа через угол?

Что же в этом замечательного? А то, что политоп с рис. 4–3 имеет бесконечное количество допустимых значений. Проверять каждое из них можно до самой смерти. Даже границы содержат бесконечное количество точек! Но углов всего 4. В одном из них и кроется оптимальное решение нашей проблемы.

Оказывается, для проверки углов существует специальный алгоритм. И он весьма эффективен даже в задачах с сотнями миллионов решений! Называется этот алгоритм симплексным методом.

Смысл его заключается в следующем: начиная с угла политопа он скользит по краям по направлению увеличения целевой функции. Когда ему встречается угол, чьи стороны направлены в противоположном направлении – он считает его лучшим.

В случае торговли автоматами и маслом, предположим, мы начали с точки (0,0). Это угол, но он приносит $0 прибыли. Безусловно, вы можете лучше.

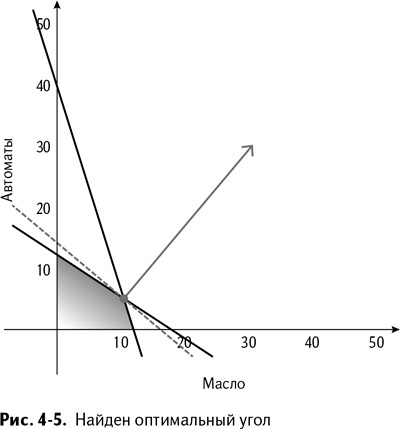
Как видно на рис. 4–3, на нижнем краю политопа прибыль увеличивается по мере движения вправо. Поэтому, двигаясь по нижней границе вправо, мы встречаем угол (14,0) – 14 бочек масла и никаких автоматов, что приносит прибыль в $2100 (рис. 4–4).

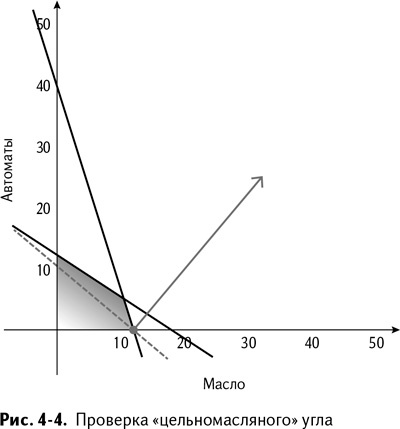
От этого «масляного» угла двигаемся в направлении увеличения прибыли по линии ограничения объема подвала. Следующий угол на нашем пути – (12,9; 3,4), который обещает доход, немного не дотягивающий до $2600. Обе стороны угла направлены в стороны с меньшей прибылью, так что мы на месте. Согласно рис. 4–5, это оптимум!

Работа в Excel

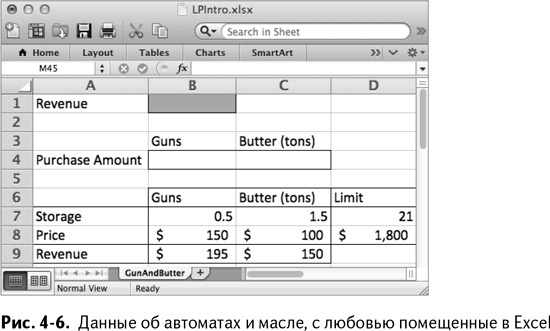
Перед тем, как перейти от этой небольшой задачи к вещам более серьезным, я хочу построить и решить ее в Excel. Первое, что вам нужно сделать на чистом листе – это создать пространство для целевых переменных и переменных решения. Назовите ячейку В2 местом, куда будет записываться общая прибыль, а ячейки В4:С4 – областью, куда будут занесены решения по продукции.

Под целевой секцией и секцией решения добавьте информацию о размерах и стоимости автоматов и масла, ограничения площади для хранения и бюджета, а также вклад каждого вида товара в прибыль.

Готовая для заполнения таблица должна выглядеть как на рис. 4–6.

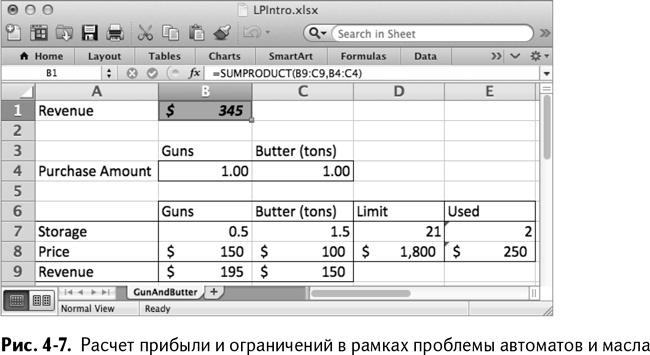
К этим данным следует добавить немного расчетов, а именно расчет ограничений и расчет прибыли. В столбце Е, следом за ячейками с ограничениями Limit, умножьте количество произведенных автоматов и масла на их относительный объем и стоимость, а затем сложите все полученное в столбце Used. Например, в ячейку Е 7 можно записать используемую площадь подвала с помощью формулы:

=SUMPRODUCT(B4:C4,B7:C7)

=СУММПРОИЗВ(B4:C4,B7:C7)

Замечу, что эта формула является линейной, потому что только одна область, В4:С4, – область решения. Другая область просто содержит коэффициенты хранения. Вы можете произвести аналогичные вычисления, чтобы узнать общую сумму, потраченную на масло и автоматы.

Для вычисления целевой функции вам нужно взять SUMPRODUCT/СУММПРОИЗВ от заказанного количества в строке 4 с прибылью в строке 9. Ввод допустимых значений, таких как 1 автомат и 1 бочка масла, дает нам лист с решением, как на рис. 4–7.

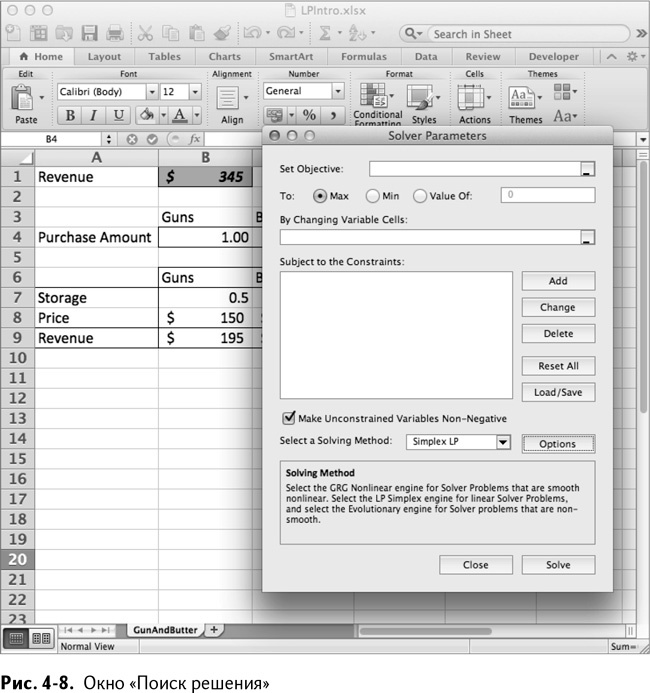
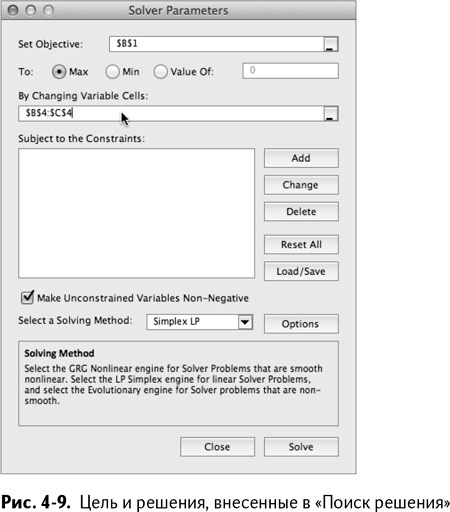
Хорошо, но как теперь заставить Excel установить оптимальные значения переменных решения? Для этого есть «Поиск решения»! Начните с открытия пустого окна «Поиска решения» (как на рис. 4–8). Подробнее об использовании этой опции читайте в главе 1.

Как упоминалось выше, необходимо снабдить «Поиск решения» целью, формулировкой задачи и условиями. Цель – прибыль, ячейка В1. Также убедитесь, что выбрали опцию «Max» и максимизируете, а не минимизируете свою прибыль в расчетах. Если бы вам в очередной задаче пришлось рассчитывать себестоимость или риски в качестве целевой функции, вы бы использовали опцию «Min».

Решения находятся в В4:С4. После того, как вы добавили их в поле «Изменяя ячейки», окно «Поиска решения» должно выглядеть как на рис. 4–8.

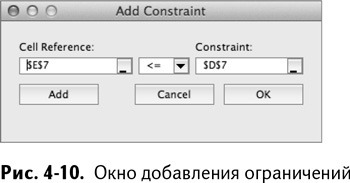
Что касается ограничений, то их вам нужно добавить два. Начните с ограниченного объема подвала. Нажмите кнопку «Добавить» рядом с полем ограничений. При заполнении небольшого поля следует указать, что значение в ячейке Е7 должно быть меньше или равно (<=) значению в ячейке D7 (рис. 4-10), а объем используемой площади – меньше ограничения.

Заметка

Обратите внимание, что «Поиск решения» добавит абсолютные ссылки ко всем переменным в ваших формулах. И это ничего не меняет. Если честно, я не знаю, зачем он это делает, потому что вы не можете перетаскивать формулы в контексте модели «Поиска решения». Для более подробного описания абсолютных ссылок обратитесь к главе 1.

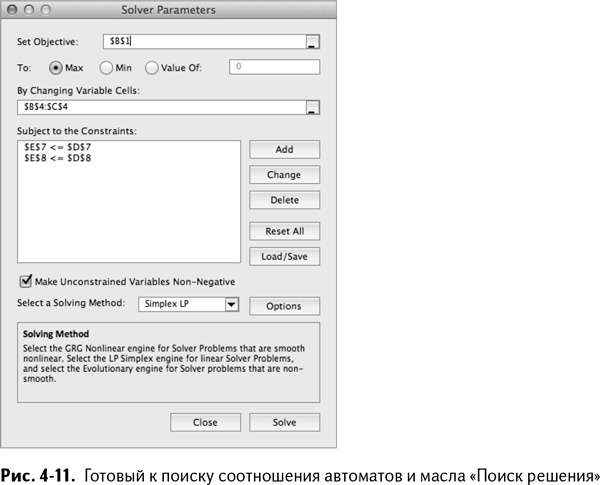
Нажмите «ОК», добавив ограничение, а затем точно так же добавьте бюджетное ограничение (Е 8 ≤ D8). Убедитесь, что отмечена опция «Сделать переменные без ограничений неотрицательными», чтобы количество произведенных автоматов и масла не стало вдруг отрицательным по непонятной причине (вы можете добавить ограничение В4:C4 ≥ 0, но просто отметить опцию проще).

Заметка

Перед тем, как нажать «ОК», посмотрите, какие еще типы ограничений предлагает вам «Поиск решения». Кроме стандартных ≤, ≥ и = есть довольно занятные, например int, bin и dif. Эти странные условия можно поместить в ячейки, чтобы значения стали целыми, бинарными (0 или 1) или «все разные». Запомните условие «int». Немного погодя мы к нему вернемся.

Теперь выберем способ решения – это должен быть «поиск решения линейных задач симплекс-методом». Все готово (рис. 4-11)!

Использование Excel 2007

В Excel 2007 нет опции «Сделать переменные без ограничений неотрицательными». Вместо этого откройте настройки «Поиска решения» и снимите галочку с опции «Неотрицательные значения». Также здесь нет возможности выбора метода решения. Вместо этого поставьте галочку «Линейная модель», чтобы включить симплексный алгоритм.

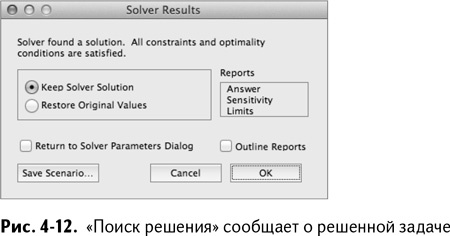
После нажатия кнопки «Выполнить» Excel быстро находит решение проблемы и открывает окошко, чтобы сообщить вам об этом. Вы можете либо принять это решение, либо изменить значения переменных решения (рис. 4-12). Если вы нажмете «ОК» и примете это решение, то увидите, что оно состоит из 3,43 автомата и 12,86 бочек масла, в точности как на вашем графике (рис. 4-13).

Но вы же не можете сделать 3,43 автомата!

Теперь ваше французское альтер эго наверняка кричит: «Zut alors! Черт возьми!» Но почему? Да потому что вы не можете сделать 43 % автомата. Я поясню этот момент.

Во время работы с линейным программированием мы частенько получаем дробные значения решений, что, безусловно, раздражает. Если бы вы производили миллионы автоматов и бочек масла, то это можно было бы проигнорировать без особого ущерба для решения и размера прибыли. Но в нашем случае числа настолько малы, что приходится заставлять «Поиск решения» делать их целыми.

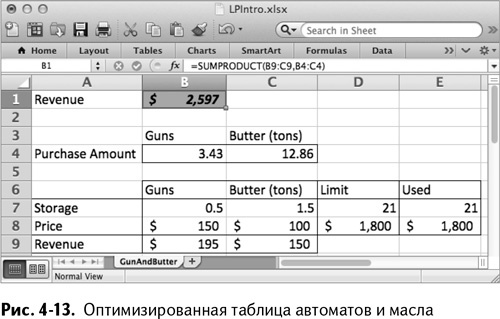
Так что возвращаемся к окошку «Поиска решения» и добавляем целочисленное ограничение для ячеек В4:С4 (рис. 4-14). Нажмем «ОК», чтобы вернуться к окошку параметров «Поиска решения».

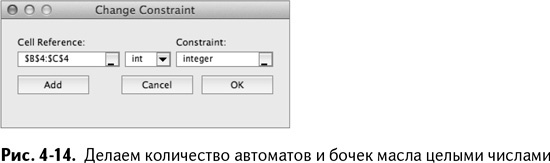
В параметрах раздела «Поиск решения задач симплекс-методом», есть опция «Игнорировать целочисленные ограничения». Убедитесь, что она не отмечена. Нажмите «ОК».

Запустите «Поиск решения» – и тут же выскочит окошко с ответом. Прибыль в нем равна $2580, что значит, вы теряете всего около $17. Неплохо! Заметьте, что вводя целочисленное ограничение, вы не можете увеличить прибыль, а только уменьшите, так как накладываете еще одно ограничение на готовое решение.

Автоматов стало больше на целых 4 штуки, а вот масло уменьшилось до 12 бочек. И, несмотря на полностью израсходованный бюджет, у вас остался еще неиспользованный кубометр подвала!

Так почему же не делать все решения целыми числами? Ну, на самом деле, это нужно далеко не всегда. К примеру, если вы смешиваете жидкости, дробные значения совсем не мешают.

Тайком от вас «Поиск решения» все же рассчитывает дробные результаты, а уж потом применяет ограничения. Алгоритм, который он использует, если встречает целочисленные или бинарные ограничения, называется «Ветви и границы», и работает он таким образом, что запускает один и тот же линейный алгоритм над разными частями исходной задачи, пока не найдет целочисленные решения для каждого этапа.

Просто для смеха сделаем нашу задачу нелинейной

Даже несмотря на то, что вы добавили целочисленное ограничение решения, основная проблема все же осталась линейной.

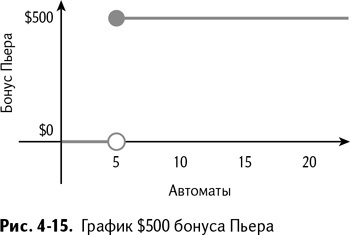
Допустим, вы будете получать призовые $500 от вашего доверенного Пьера, если каждый месяц сможете делать на 5 автоматов больше. Добавьте функцию IF/ЕСЛИ в ячейку с прибылью, которая поступает от производства автоматов – В4:

=SUMPRODUCT(B9:C9,B4:C4)+IF(B4>=5,500,0)

=СУММПРОИЗВ(B9:C9,B4:C4)+ЕСЛИ(B4>=5,500,0)

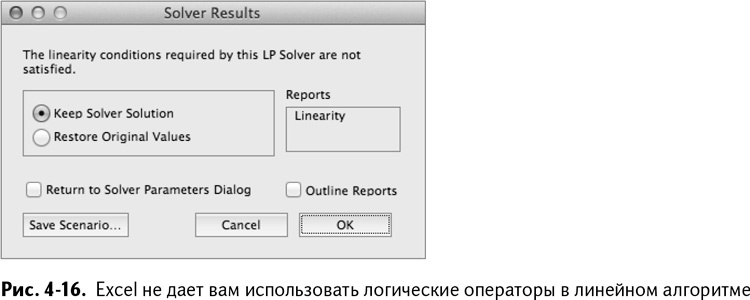
Как только вы добавляете это условие – IF/ЕСЛИ – целевая функция становится нелинейной. Оно изображено на графике (рис. 4-15), где вы можете легко увидеть большой нелинейный разрыв в точке 5 автоматов.

Если бы вы попытались открыть «Поиск решения» и снова использовать линейный симплексный алгоритм для решения этой задачи, Excel бы вежливо пожаловался на то, что «не выполнены условия линейности, требуемые алгоритмом» (рис. 4-16).

К счастью, для решения этой задачи у «Поиска решения» есть два других алгоритма, а именно «Эволюционный» и «Поиск решения нелинейных задач методом ОПГ». На этот раз мы дадим шанс эволюционному алгоритму, с которым уже знакомы по главе 2 (в Excel 2007 нет возможности выбора алгоритма, поэтому просто снимите галочку с опции «Линейная модель»).

Работа эволюционного алгоритма приблизительно повторяет принципы работы биологической эволюции:

• генерирует пул исходных решений (что-то вроде генетического пула) разной степени вероятности;

• каждое решение имеет некий уровень пригодности к выживанию;

• решения размножаются перекрестным переносом, то есть их компоненты выбираются из двух или трех существующих решений и затем комбинируются;

• существующие решения мутируют в новые;

• имеет место локальный поиск, в процессе которого генерируются новые решения вблизи лучшего на данный момент решения в популяции;

• происходит отбор: случайно выбранные неуспешные кандидаты в решения выбрасываются из генетического пула.

Обратите внимание, что в данном приближении нет наследования типа алгоритма: линейного, квадратичного или какого-то еще. В какой-то степени каждая задача может рассматриваться как черный ящик.

Это означает, что, моделируя задачи линейного программирования в Excel, вы ограничены такими условиями, как знаки +/-, формулами SUM/СУММА и AVERAGE/СРЗНАЧ, где решения находятся только в рамках одной последовательности. Но если вы используете эволюционный алгоритм, выбор доступных формул существенно увеличивается. Вы можете применить любую функцию, какую только захотите, в том числе эти полезные нелинейные функции.

Логические проверки:

• IF/ЕСЛИ

• COUNTIF/СЧЁТЕСЛИ

• SUMIF/СУММЕСЛИ

Статистические функции:

• MIN/МИН

• MAX/МАКС

• MEDIAN/МЕДИАНА

• LARGE/НАИБОЛЬШИЙ

• NORMDIST/НОРМРАСП, BINOMDIST/БИНОМРАСП, и т. д.

Функции поиска:

• VLOOKUP/ВПР

• HLOOKUP/ГПР

• OFFSET/СМЕЩ

• MATCH/ПОИСКПОЗ

• INDEX/ИНДЕКС

Я вижу, вы уже готовы воспарить от восторга, так что позвольте мне немного «приземлить» вас. С эволюционным алгоритмом все же возникают некоторые проблемы.

• Нет никакой гарантии, что он найдет оптимальное решение. Все, что в его силах – это контроль лучшего решения в популяции, пока не закончится время, либо популяция не изменится в достаточной степени для продолжения, либо вы принудительно не остановите «Поиск решения» нажатием кнопки Escape. Вы можете модифицировать эти критерии остановки эволюционного алгоритма в разделе параметров «Поиска решения».

• Эволюционный поиск решения работает довольно медленно. А если области допустимых значений сложные, он часто ругается, не найдя даже места, с которого начать.

• Если вы хотите заставить эволюционный алгоритм хорошо работать в Excel, вам придется определить жесткие границы для каждой переменной решения. Даже если ваше решение более или менее неограниченное, вам все же придется ограничить его каким-то большим числом.

Принимая во внимание последний пункт, для решения задачи с автоматами и маслом вам нужно добавить ограничение, согласно которому оба решения не должны быть больше 25, как показано на рис. 4-17.

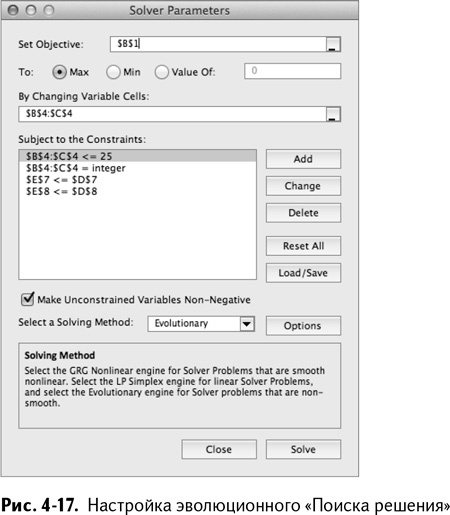
Нажмите «ОК», а затем «Выполнить». Алгоритм запущен и должен каким-то образом выдать нам решение, состоящее из 6 автоматов и 9 бочек масла. Так, эволюционный алгоритм решил отблагодарить Пьера за приз! Неплохо. Но обратите внимание, что даже такая маленькая задача заняла некоторое время. Около 30 секунд на моем ноутбуке. Задумайтесь, что это может значить для промышленной модели.

Монстр в конце главы

Все проблемы, рассмотренные нами до этого момента, были воображаемыми. В следующей части я собираюсь продемонстрировать способности «Поиска решения» на чем-то более осязаемом. Вы снова проведете какое-то время, учась моделировать нелинейные функции (вроде пьеровского бонуса) линейными способами, так что можете продолжать пользоваться «Поиском решения линейных задач симплекс-методом».

Если вы с нетерпением ждете перехода к следующей теме, обнадежу вас: сейчас вы знаете большую часть того, что нужно знать для успешного изучения последующих глав. Останьтесь со мной хотя бы до раздела с ограничениями If-Then/Если-То и «Большого М» этой главы, чтобы научиться тому, что понадобится в главе 5 для кластеризации графов. А еще лучше – втягивайтесь и работайте над всеми оставшимися задачами вместе со мной! Сразу предупреждаю: два последних смоделированных бизнес-правила в этой главе – настоящие монстры!

Другие инструменты

Большие модели не очень-то хорошо идут в Excel. Версия «Поиска решения», встроенная в него, позволяет иметь только 100–200 переменных решений и ограничений, в зависимости от версии. Это ограничивает размер задач, с которыми вы сталкиваетесь в этой книге.

Если вы хотите и дальше пользоваться Excel, купите расширенную версию «Поиска решения» у Frontline Systems. Еще лучше, особенно если у вас Windows, использовать OpenSolver, как мы будем делать в конце этой главы. OpenSolver, описанный в главе 1, обращается к открытому ресурсу под названием COIN Branch and Cut ( ), который идеален для проблем оптимизации среднего размера. Я вполне эффективно использовал OpenSolver для сотен и тысяч переменных.

Есть и программы для линейного программирования пожирнее, например Gurobi и CPLEX. Разработчикам и остальным любителям «облачных сервисов» я особо рекомендую Gurobi, ибо CPLEX, принадлежащий IBM, – лучшее корпоративное решение.

Интерфейс у таких мощных промышленных программ встречается разный. К примеру, CPLEX идет в пакете со средой OPL, где можно писать модели на специальном языке, имеющем прекрасную привязку к электронным таблицам. В языках программирования есть множество подобных привязок для связи алгоритмов с моделями внутри промышленных систем.

Мой любимый инструмент для встраивания в мощные системы поиска решений, такие как СPLEX и Gurobi, называется AIMMS ( ). Программа позволяет построить свою оптимизационную модель, а затем «шлепнуть» на нее пользовательский интерфейс без необходимости писать его код. Также эта программа может общаться с электронными таблицами и базами данных.

До конца этой книги вы вполне дотянете и с Excel и его «Поиском решения». Но вам следует знать о существовании сверхсовременных сред моделирования для решения больших задач на случай, если ваши нужды перерастут Excel.

Назад: Зачем ученым, работающим с данными, нужна оптимизация?

Дальше: Свежий, из сада – прямо в стакан… с небольшой остановкой на модель смешивания