График функции потерь Тагути, показанный на рисунке 34, – это парабола, вытянутая вдоль вертикальной оси и имеющая минимальное значение, равное нулю, в точке номинального значения показателя качества. Уравнение такой параболы имеет вид:

где: х – измеряемое значение показателя качества; х0 – его номинальное значение; L(x) – значение функции потерь Тагути в точке х; с – коэффициент масштаба (подбираемый в соответствии с используемой денежной единицей при измерении потерь). Это наиболее естественная и простая математическая функция, пригодная для представления основных особенностей функции потерь Тагути, рассмотренных в главе 11. Конечно, это не означает, что такой ее вид – наилучший выбор в каждом конкретном случае ее применения. Отметим, например, тот факт, что вышеприведенная формула предполагает одинаковый уровень потерь при отклонениях от номинала в обе стороны (в конце предшествующей главы мы рассматривали конкретный случай, когда это предположение не выполняется). С другой стороны, хотя данная модель часто служит разумным приближением для показателя качества в пределах его допусков и на не слишком большом удалении от границ допуска, она, очевидно, не подходит для больших отклонений от номинального значения. Однако наши процессы не столь уж плохи, чтобы нам требовалось рассматривать такие значительные отклонения.

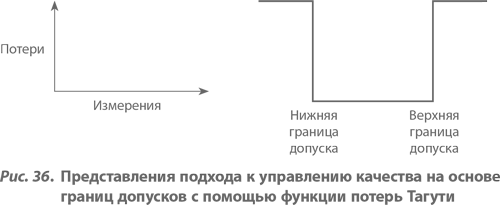
Но даже если наша параболическая модель и не вполне корректна, она, без сомнения, значительно ближе к действительности, чем функция потерь, соответствующая подходу к качеству на основе установления границ допусков, представленная на рисунке 36. Последняя модель предполагает, что потери отсутствуют при всех отклонениях от номинала в пределах допусков, но они скачкообразно возникают на границах поля допуска. С учетом проведенного в предшествующей главе обсуждения здесь не нет нужды в детальном рассмотрении данного вопроса, за исключением одного аспекта. Припомните сделанное нами в главе 11 наблюдение об осознании важности допусков. В любой системе, механической или бюрократической, которая спохватывается, только когда что-либо выходит за границы допусков, скоропалительные действия оказываются весьма дорогостоящими. Значит, в подобных случаях действительно имеется резкое увеличение потерь после выхода показателя качества за границы допусков, но эти потери обусловлены самой системой управления, а не возникают в результате отклонений уровня качества самой продукции или услуги.

Ниже мы воспользуемся параболической моделью для более детального изучения понятий и примеров, рассмотренных в главе 11. Поскольку это всего лишь модель, конкретные числа, получаемые в ходе расчетов, не так уж важны. Поэтому незначительные отличия в числах не будут рассматриваться как что-то значимое. Стратегия, дающая несколько большие потери, чем другая стратегия в предположении применимости этой модели, при замене этой модели на другую может оказаться более предпочтительной для функции потерь. Но когда мы обнаруживаем различия на целые порядки (например, когда потери от одной стратегии в 10, 50 или даже 100 раз превышают потери от другой), мы можем с полной уверенностью сказать, что различия в стратегиях весьма значительны, даже с учетом того, что параболическая модель – всего лишь идеализация.

В качестве дальнейшей идеализации, которая нужна для проведения численных сравнений в данной главе, мы вынуждены предположить, что рассматриваемые здесь процессы будут абсолютно стабильными. Приведенный в главе 4 термин «абсолютно стабильный» предполагает, что статистическое распределение процесса неизменно, не колеблется. В частности, это означает, что мы можем говорить в терминах истинных значений для среднего и стандартного отклонения, которые мы обозначим (но только в данной главе) символами μ и σ соответственно. (Хотя это противоречит важному замечанию Деминга касательно реальных процессов; см.: «Выход из кризиса», стр. 293.)

Далее мы будем использовать понятие средних потерь Тагути. Средние потери Тагути, применительно к выборке или партии из n изделий, для которых значения х1, х2…, хn рассматриваемого показателя качества х равны:

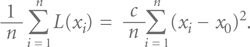
Если процесс абсолютно стабилен и имеет плотность распределения вероятности, тогда средние потери Тагути можно вычислить из:

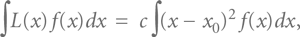
что соответствует площади под кривой, задаваемой произведением функции потерь L(x) на плотность вероятности f(x). Некоторые очевидные математические преобразования позволяют привести это выражение к виду:

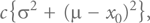
где члены внутри фигурных скобок ({…}) представляют соответственно квадратичное (стандартное) отклонение (обычно связанное с дисперсией) и квадрат смещения. Следует заметить, что средние потери Тагути не зависят каким-то сложным образом от f(x); их можно весьма просто вычислить, если известны простые параметры, входящие в последнее выражение.

Чтобы облегчить сравнения, давайте также введем обозначение для воспроизводимости процесса. В разных компаниях она определяется различным образом, но мы будем полагать ее равной разности между верхней и нижней границами допуска деленной на разность между верхней и нижней естественными пределами процесса, где для естественных пределов процесса мы используем «истинные» границы 3σ для индивидуальных наблюдений, так что знаменатель можно представить просто как 6σ.

Воспроизводимость, равная 1 (единичная воспроизводимость), соответствует процессу, который в большинстве случаев едва укладывается в границы допусков. Процесс иногда называют воспроизводимым или невоспроизводимым в зависимости от того, превосходит ли показатель воспроизводимости единицу или нет. Обычный образ мыслей на Западе – признание значения 1 1/3 как соответствующего исключительно эффективному процессу, а значения 1 2/3 – уже, возможно, слишком экстравагантным, поскольку вероятность получения в этом случае измерения за пределами допусков оказывается пренебрежимо малой. Однако заметим, что данные о процессах из японской практики, упоминаемые в главе 11, позволяют оценить их уровень воспроизводимости от 3 до 5. И чтобы мера воспроизводимости отражала то, что процесс может давать на самом деле (а не то, на что он потенциально способен), надо предположить, что процесс точно настроен (центрирован), т. е. среднее процесса совпадает с номинальным значением х0. Ниже мы рассмотрим, что происходит, если это предположение не выполняется.

Мы должны выбрать значение масштабного коэффициента с в уравнении для параболы таким образом, чтобы процесс, имеющий воспроизводимость 1 и точно центрированный, имел бы средние потери Тагути, равные 100 единицам. Вначале рассмотрим значения средних потерь Тагути для абсолютно стабильного процесса, точно настроенного на номинальное значение ху, но в предположении различной воспроизводимости процесса.

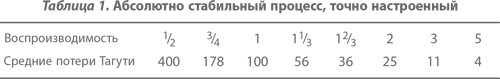
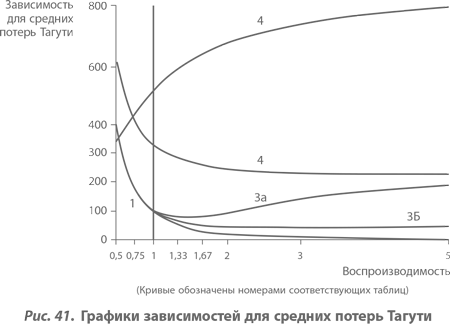
Мы видим, что повышение воспроизводимости от 1 1/3 до 1 2/3 уменьшает средние потери Тагути от половины до трети их значения по сравнению с потерями, соответствующими единичной воспроизводимости. Однако повышение воспроизводимости до 3–5 дает огромный эффект, описываемый в терминах порядков величин, как мы говорили об этом ранее. Графики средних потерь Тагути, в зависимости от воспроизводимости процессов, для всех примеров, рассматриваемых в данной главе, показаны на рисунке 41.

Важность точной настройки (центрирования) процесса можно быстро оценить, сравнивая данные таблиц 1 и 2. Данные таблицы 2 рассчитаны в предположении, что процесс неточно настроен и центрирован в середине диапазона между номиналом и одним из пределов допуска.

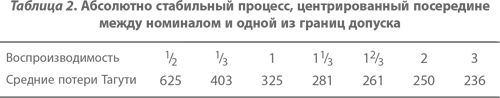
Плохая настройка процесса полностью разрушает все потенциальные преимущества улучшения воспроизводимости. Однако даже при такой плохой настройке процесс, имеющий воспроизводимость 2 и выше, практически не будет давать изделий, выходящих за границы допусков. Поэтому, хотя такой процесс рассматривался бы как безусловно выдающийся с точки зрения удовлетворения заданных допусков, – рассмотренный с позиций функции потерь Тагути он, безусловно, намного хуже, чем точно настроенный процесс; например, для эффективности, равной 2, потери в таблице 2 в десять раз превышают потери, приводимые в таблице 1.

Теперь мы рассмотрим два примера, описанные в конце предшествующей главы. Сначала обратимся к проблеме износа инструмента. Припомним детали: первоначально процесс настроен так, чтобы результаты измерений были близки к верхней границе допуска (ВГД). Затем износ инструмента будет приводить к постепенному уменьшению значений; когда результаты начинают приближаться к нижней границе допуска (НГД), процесс останавливается и инструмент заменяется. Отметим, что воспроизводимость рассматриваемого процесса (без учета его дрейфа) должна быть больше 1, чтобы такую схему вообще можно было реализовать, иначе возможность для маневрирования просто отсутствовала бы. Для полноты картины ниже мы рассмотрели также случай, соответствующий единичной воспроизводимости.

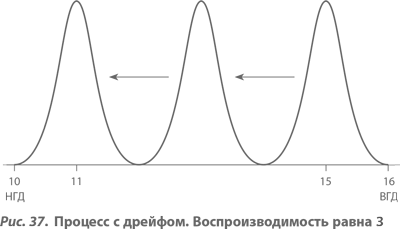
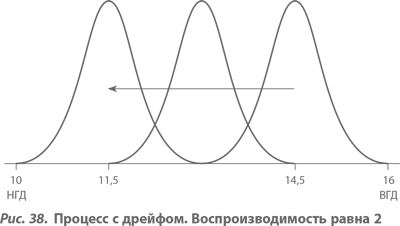
На рисунке 37 показан случай, когда воспроизводимость процесса равна 3. Для примера мы принимаем значения НГД и ВГД равными 10 и 16 соответственно, а стандартное отклонение σ – равным 1/3 (если бы σ была равна 1, то воспроизводимость процесса также была бы равна единице). Первоначально мы настраиваем центр распределения на 15, так что распределение попадает как раз ниже ВГД. Предположим, что среднее процесса с постоянной скоростью смещается вниз, к значению 11, и в этот самый момент мы останавливаем процесс, меняем инструмент и вновь настраиваем его на 15. (Если бы эффективность процесса была 2 вместо 3, т. е. σ = 0,5, тогда мы были бы должны первоначально установить центр процесса на 14,5 и позволить ему затем смещаться вниз, до 11,5, когда пора заменять инструмент. Этот случай представлен на рисунке 38.) Средние потери Тагути для процессов с различной воспроизводимостью, которыми «управляют» таким образом, представлены в таблице 3а. (При этом стоимость замены инструмента в явном виде при расчетах не учитывалась.)

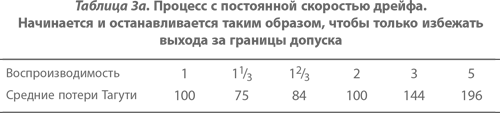
Но что за сюрприз! Для малых значений воспроизводимости потери Тагути вначале уменьшаются, но вскоре начинают увеличиваться, так что потери для процесса с воспроизводимостью 5 оказываются более чем в два раза бо́льшими, чем для процесса с воспроизводимостью, равной 1! По здравом размышлении причина такого увеличения становится ясной. Когда воспроизводимость процесса велика, его первоначальная настройка дает значения, очень близкие к ВГД, таким образом, он принужден давать изделия с параметрами, сильно отличающимися от номинальных, что соответственно приводит к высоким потерям Тагути. То же справедливо, когда процесс уже сместился к НГД в моменты, непосредственно предшествующие смене инструмента. Вследствие квадратичного характера функции потерь ущерб, вызванный этими экстремальными ситуациями, превышает выгоды от получения хороших изделий в моменты, когда процесс находился вблизи номинального значения, на полпути от ВГД к НГД.

Отметим, что полученный вывод находится в прямом противоречии с миром, основанным на использовании модели соответствия требованиям допусков. Сама схема организована таким образом, чтобы вне зависимости от того, какова воспроизводимость процесса (коль скоро она превышает 1), не производилось бы продукции, выходящей за границы допусков. Увеличение показателя воспроизводимости процесса с этой точки зрения имеет то положительное следствие, что процесс может длиться дольше до момента, когда возникает потребность в замене инструмента. Однако, как мы теперь видим, эта выгода ложна с точки зрения потерь Тагути. Средние потери Тагути существенно снизятся, если мы сможем, например, менять инструмент в два раза чаще. Так, для процесса с воспроизводимостью 3 это позволит настроить его первоначально на 14 (а не на 15) и заменить его, когда среднее значение снизится до 12 (а не до 11). Средние потери Тагути будут в этом случае равны 44 вместо 144, хотя это все еще и близко не подходит к результату, который дает процесс с воспроизводимостью 3 без смещения (в этом случае, в соответствии с таблицей 1, средние потери Тагути равны 11). В то же время это существенное улучшение по сравнению с тем, что получается, если мы ждем до возможного предела, прежде чем сменить инструмент. Таблица 3Б показывает результат в два раза более частой смены инструмента для тех же значений воспроизводимости, что в таблице 3а.

Стоит ли существенное уменьшение средних потерь Тагути по сравнению с потерями, соответствующими в таблице 3а, тех дополнительных затрат, которые возникают из-за в два раза более частой замены инструмента? На этот вопрос должен дать ответ тот, кто руководит системой.

И наконец, мы подошли к рассмотрению операции обрубки. Вспомним, что среднее процесса было настроено на значение, превышающее номинал, в силу той очевидной логики, что легче укоротить длинный пруток, чем удлинить короткий. Давайте смоделируем этот случай, предположив, что среднее значение процесса обрубки установлено на ВГД, и, если длина прутка оказывается больше, чем верхний допуск, тогда от него отрубается дополнительный отрезок, равный интервалу допуска (т. е. разности между ВГД и НГД). Конечно, это тоже весьма упрощенная модель, но результат очень интересный и достаточно хорошо согласуется с той реальной ситуацией, которая послужила поводом для настоящего рассмотрения.

Проблема, связанная с данной схемой, легко обнаруживается при рассмотрении двух рисунков. Распределение, соответствующее первой обрубке, представлено на рисунке 39. После того как сделана повторная обрубка для половины прутков, оказавшихся чересчур длинными, длины оставшихся прутков имеют распределение, показанное на рисунке 40.

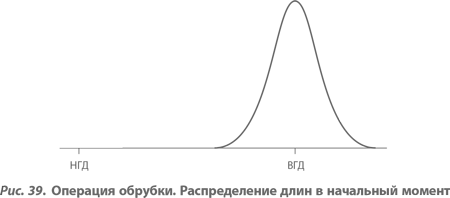
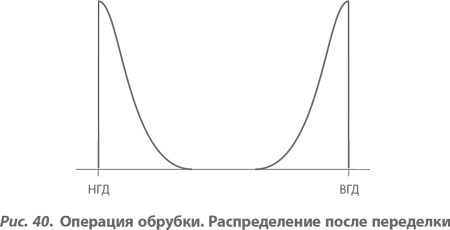
Отсюда становится понятно, почему средние потери Тагути оказываются такими высокими (см. табл. 4). Для большинства прутков их длины оказываются близкими к границам допусков, и лишь для очень малого их числа вообще имеют место случаи, когда их длина оказывается близкой к номиналу. Другими словами, большинство прутков имеет длины, дающие максимальные значения функции потерь из всех возможных значений внутри диапазона допусков. В то же время практически отсутствуют прутки с длинами, дающими малый вклад в среднюю функцию потерь. Так же как и в предшествующем случае, для читателя должно быть очевидно, что это еще один случай, когда увеличение воспроизводимости процесса на самом деле лишь ухудшает положение дел.

Как мы видим, система, которая вполне приемлема с точки зрения удовлетворения требованиям допусков, дает плачевный результат в терминах функции потерь Тагути.

Как отмечалось ранее, на рисунке 41 показаны графики зависимостей средних потерь Тагути для всех примеров, которые мы исследовали в данной главе. Бросаются в глаза огромные различия, которые, однако, скрыты от нас, если мы удовлетворяемся лишь требованиями допусков (спецификаций).