Если некоторая величина зависит от двух величин, то ее называют функцией двух переменных, которые, в свою очередь, называют аргументами. Например, если мы приобретаем количество х одного товара по цене 3 и количество у второго товара по цене 5, то для покупки набора (х, у) мы затрачиваем сумму, равную Q= Зх + 5у. Таким образом, затрата Q является функцией двух переменных х и у.

Графиком функции двух переменных является поверхность в пространстве. Изобразить эту поверхность не всегда просто, да и польза от нее в смысле наглядности невелика. Поэтому функцию двух переменных характеризуют линиями уровня, или линиями безразличия. Что это такое, поясним на примере функции затрат.

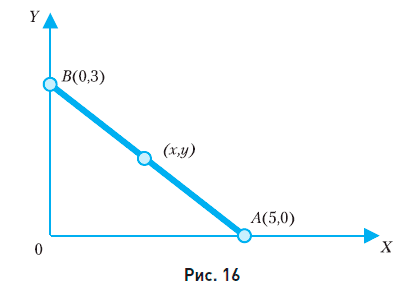
Предположим, что наша затрата равна Q = 15. Если весь этот капитал мы потратили на один товар, то наш набор будет такой: х = 5; у = 0. Этому набору соответствует точка А(5, 0) на оси X (рис. 16).

Если же весь наш капитал мы потратили на другой товар, то наш набор будет такой: х = 0, у = 3. Этому второму набору соответствует точка В(0, 3) на оси Y (см. рис. 16).

Прямая, соединяющая точки А и В, является линией безразличия для функции затрат Q = Зх + 5у, так как все точки (х, у) этой прямой соответствуют равноценным наборам с одной и той же ценой Q = 15.

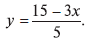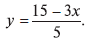Уравнение линии безразличия имеет вид Это уравнение можно получить из равенства 15 = Зх + 5у.

В качестве другого примера функции двух переменных рассмотрим функцию полезности. Приобретая набор (х, у), мы преследуем определенную цель: получить максимальное содержание белка, если это набор кормов, максимальную прочность сплава, если это набор двух металлов, минимальную теплопроводность, если это набор двух материалов для теплоизоляции, и т. д.

В любом случае полезность U есть величина, значение которой зависит от величин х и у. Это означает, что полезность Uявляется функцией двух переменных. Обычно считается, что полезность должна быть пропорциональна как х, так и у. Таким свойством обладает функция U = ху (функция Кобба – Дугласа).

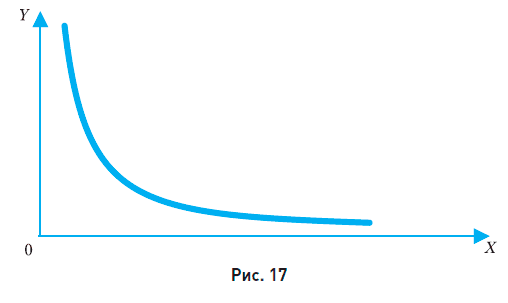
Построим кривую безразличия для этой функции. Предположим, что от набора (х, у) мы хотим получить полезность, равную U= 12. Нетрудно убедиться, что каждый из наборов (1,12), (2, 6), (3, 4), (4, 3), (6, 2), (12, 1) дает значение полезности U= 12, т. е. в отношении полезности нам безразлично, какой из этих наборов приобрести. Поэтому кривая, проходящая через эти точки, будет линией безразличия для функции полезности U = xy (рис. 17).

От функции одной переменной мы находили производную, т. е. дифференцировали эту функцию (см. п. 2).

Функцию двух переменных также можно дифференцировать по одной из переменных, считая другую постоянной. Получающаяся при этом функция называется частной производной.

Задача 14. Найти частные производные от рассмотренных функций затрат и от функции полезности.